一种用于数字D类功放的伪自然采样算法

于泽琦樊养余 史龙飞 吕国云

(西北工业大学电子信息学院 西安 710129)

1 引言

数字D类功放由于高电源效率和便于与数字音频信号源接口匹配，受到消费类音频电子产品的青睐并成为研究热点[1-3]。数字D类功放由全数字电路实现的开关信号调制器、功率级和模拟低通滤波器组成。数字D类功放把数字音频信号调制成开关信号的方法主要有：脉冲密度调制(Pulse Density Modulation, PDM)[4,5],Click调制(Click Modulation,CM)[6,7]和均匀采样脉冲宽度调制(Uniform sampled Pulse Width Modulation, UPWM)[1-3,8-15]。由于UPWM 方法相比其它方法有生成的开关信号脉冲重复频率低且实现简单的优点，所以数字D类功放通常采用 UPWM 方法实现开关信号调制器。然而直接对数字音频信号进行UPWM，数字D类功放需要很高的时钟频率，所以数字D类功放通常使用过采样和量化噪声压缩技术，在基本不影响音频带宽内所携信息的情况下降低数字音频信号的位数，从而使系统容易实现[8]。此外，由于UPWM是一种非线性的调制方法，数字D类功放在信号调制时会产生失真，所以还需对其产生的失真进行校正[9]。目前，针对 UPWM 失真的校正算法，主要有：伪自然采样算法[913]-、闭环负反馈算法[2]、前置均衡器算法[14]和预校正算法[15]。伪自然采样算法相比其它校正算法，有实现简单且校正效果良好的特点，广泛应用在数字D类功放中。

本文首先介绍用于UPWM型数字D类功放的伪自然采样算法原理以及目前存在的伪自然采样算法，再针对现有算法的不足，提出一种新的伪自然采样算法，然后对其进行实验验证，最后给出结论。

2 伪自然采样算法原理

单边后沿自然采样脉冲宽度调制(Natural sampled Pulse Width Modulation, NPWM)和UPWM的调制过程如图1所示。图1中，为输入信号，和为经过以采样频率cf采样后的任意两点，为载波。假定载波频率为cf，输入信号为频率是xf的正弦信号。由图1可知，在时间段内，NPWM信号的脉冲宽度由与的交点(自然采样点)决定，而UPWM信号的脉冲宽度由与的交点(均匀采样点)决定。文献[16]利用双重傅里叶级数对如图1所示NPWM和UPWM进行了分析，由分析可知，在信号带宽内，UPWM信号的频谱由直流成分、输入信号的基波及其谐波成分以及载波与输入信号的互调谐波成分构成；而NPWM信号的频谱仅由直流成分、输入信号的基波成分以及载波与输入信号的互调谐波成分构成；NPWM和UPWM信号的互调谐波幅度随次数的增大而减小。由于 NPWM 信号不含输入信号的谐波成分，所以当高倍过采样后的输入信号经 NPWM后，其在信号带宽内的失真可忽略不计。

图1 单边后沿NPWM和UPWM的调制过程示意图

虽然NPWM相比UPWM有较好的抑制谐波特性，但由图1可知，由于数字D类功放的输入信号为数字信号，所以数字 D类功放只能使用UPWM。于是，数字D类功放可运用伪自然采样算法对其 UPWM 前的信号进行预处理，在每个载波周期内得到近似于自然采样点的伪自然采样点，使其开关信号在时域上逼近 NPWM 信号，从而消除开关信号的输入信号谐波成分。目前存在的伪自然采样算法主要有：一阶拉格朗日插值(LAGrange Interpolation, LAG-I)算法[9]，δ补偿(δ Compensation, δC)算法[10]，LAG-NR 算法[11,12]，迭代线性内插(Iterative Linear Interpolation, ILI)算法[13]等。一阶LAG-I算法通过对相邻输入两点进行一阶拉格朗日插值逼近输入信号原波形，然后求逼近后的波形与载波的交点以产生开关信号，由于逼近精度较差，对输出信号的谐波失真改善较小；δC算法利用几何方法近似求出当前均匀采样点幅值相对其自然采样点幅值的差值δ，然后把δ补偿到当前均匀采样点幅值上使最终得到的开关信号逼近 NPWM 信号，由于每个δ的计算只用到两个输入点，同样谐波校正效果较差；LAG-NR算法用高阶拉格朗日插值法逼近输入信号原波形，再利用Newton-Raphson算法经过单次迭代寻找伪自然采样点，从而使输出可获得较低的谐波失真，但其含较多的乘法和除法运算，计算复杂度较高；ILI算法通过对输入2倍插值滤波和利用二阶拉格朗日插值法迭代寻找伪自然采样点校正输出信号的谐波失真，由于其在计算伪自然采样点时使用的非相邻输入点信息较少，使输出仍留有一定的谐波成分。

3 一种新的伪自然采样算法

由上文可知，目前存在的伪自然采样算法难以兼顾低计算复杂度和低谐波失真，因此本文提出一种新的伪自然采样算法。本文提出的伪自然采样算法原理如图 2所示，假设和为输入信号以采样频率cf采样后的4个相邻点，，对此4点利用三阶拉格朗日插值多项式逼近，得

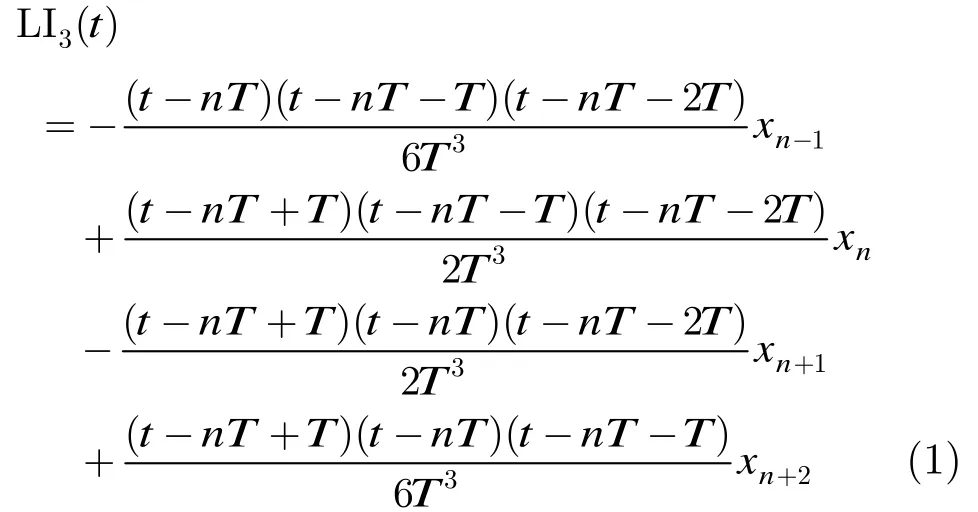
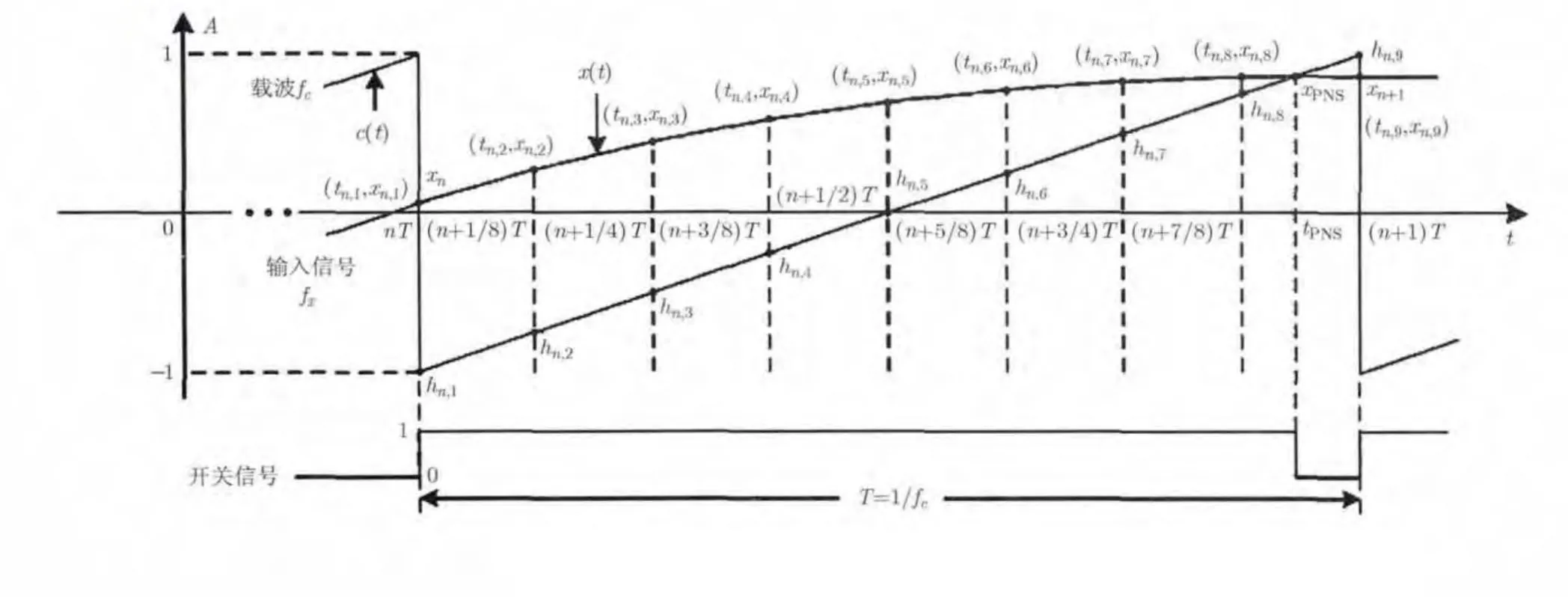
图2 本文提出的伪自然采样算法原理图

由上可知，本算法仍用到除法运算。然而，对于式(3)至式(9)所涉及的除法运算，由于其除数都为常数且都为2的幂数，所以可把其转化为简单的移位运算。对于式(11)所涉及的除法运算，可令，对展开成L阶麦克劳林级数形式：

以避免除法运算。为了简化硬件结构，可取 3L= 。把 3L= 的式(12)代入式(11)后，可知该算法仅包含乘法、加法、比较和移位运算。由于 ()c t的频率通常远小于UPWM的采样频率，故可在 ()c t周期内时分复用一个乘法器实现本算法涉及的乘法运算，这样可在不影响性能的情况下，减少硬件消耗。

4 算法验证

本文基于Altera公司型号为EP4CE30F23C6N的FPGA实现了一个UPWM型数字D类功放的开关信号调制器(主时钟频率为24.576 MHz)，并对其搭建了如图3所示的测试系统。在图3中，计算机通过同轴音频接口向数字音频接收芯片 CS8416输出采样频率为48 kHz、精度为24位的测试信号，然后 CS8416输出 I2S格式的串行数字信号到基于FPGA的开关信号调制器中，开关信号调制器把串行数字信号调制成开关信号，最后经由内部的主控数据接口模块把开关信号输出到计算机中分析。

图3 基于FPGA的开关信号调制器测试系统结构图

图4 开关信号调制器的输出频谱

图4给出了在测试信号为幅度为0 dBFS、频率为6 kHz的正弦信号的情况下，当伪自然采样模块不起作用时以及当基于一阶LAG-I算法、 Cδ算法、ILI算法(迭代次数为 16，与文献[13]所述最优迭代次数相同)、LAG-NR算法(利用三阶拉格朗日插值法，并以一阶LAG-I算法求得的伪自然采样点作为Newton-Raphson算法的初始解)和本文所述算法分别构造伪自然采样模块时，开关信号调制器的输出频谱。由图4可知，本文所述算法使谐波淹没在由于互调失真引起的本底噪声中，基本上使开关信号调制器的输出消除了谐波影响，其谐波消除效果与LAG-NR算法基本相同，且明显优于其它伪自然采样算法。

表1列出了基于不同算法的伪自然采样模块所消耗的FPGA资源以及计算每个伪自然采样点所需的时间calT ，其中mclkT 为FPGA主时钟周期(为了方便对比，所有伪自然采样模块均不使用FPGA内部乘法器)。由表1可知，在硬件消耗上，本文所述算法仅为ILI算法和LAG-NR算法的3/4左右；在计算每个伪自然采样点所需的时间上，本文所述算法与ILI算法相同，约为LAG-NR算法的3/5。由此可得，本文所述算法的计算复杂度低于 ILI算法和LAG-NR算法。

图 5为分别基于本文所述算法、ILI算法以及LAG-NR算法的开关信号调制器输出总谐波失真(Total Harmonic Distortion, THD)对比图。由图5可知，基于本文所述算法的开关信号调制器输出THD小于0.001%，与基于LAG-NR算法的开关信号调制器输出THD基本一致，且仅为基于ILI算法的开关信号调制器输出THD的一半左右。

表1 基于不同算法的伪自然采样模块所消耗的FPGA资源以及计算每个伪自然采样点所需的时间Tcal对比

图5 基于不同算法的开关信号调制器输出THD对比图

5 结论

本文提出一种新的伪自然采样算法，该算法有效解决了UPWM型数字D类功放在UPWM后使输出信号产生较大谐波失真的问题。该算法基于拉格朗日插值法和一种伪自然采样点位置判断法，并利用麦克劳林级数消除除法运算，在达到较好的谐波校正效果的同时，易于硬件实现。通过实验测试，基于本文所述算法的开关信号调制器输出 THD小于0.001%，其与高性能功率级、模拟低通滤波器连接可方便地组成高性能的数字D类功放。

[1] Liu M, Chien S, Kuo T, et al.. A 100 W 5.1-channel digital class-D audio amplifier with single-chip design[J]. IEEE Journal of Solid-State Circuits, 2012, 47(6): 1344-1354.

[2] Berkhout M and Dooper L. Class-D audio amplifiers in mobile applications[J]. IEEE Transactions on Circuits and System-Ⅰ Regular Papers, 2010, 57(5): 992-1001.

[3] Kyoungsoo P, Hah Z, and Sung K. Digital amplifier of 96 kHz PWM frequency with 91 dB dynamic range and 0.13%THD+N at full modulation[J]. IEEE Transactions on Consumer Electronics, 2012, 58(4): 1307-1313.

[4] Noh J, Lee D, Jo J, et al.. A class-D amplifier with pulse code modulated (PCM) digital input for digital hearing aid[J].IEEE Journal of Solid-State Circuits, 2013, 48(2): 465-472.[5] Pracny P, Muntal P, and Bruun E. Interpolation filter design for hearing-aid audio class-d output stage application[C].Proceedings of 19th IEEE International Conference on Electronics, Circuits, and Systems, Seville, 2012: 364-367.

[6] Sozanski K. A digital click modulator for a class D audio power amplifier[C]. Proceedings of 13th IEEE Conference on Signal Processing: Algorithms, Arrangement, and Applications, Poznan, 2009: 121-126.

[7] Stefanazzi L, Oliva A, and Paolini E. Alias-free digital click modulator[J]. IEEE Transactions on Industrial Informatics,2013, 9(2): 1074-1083.

[8] Dooper L and Berkhout M. A 3.4 W digital-in class-D audio amplifier in 0.14 μm CMOS[J]. IEEE Journal of Solid-State Circuits, 2012, 47(7): 1524-1534.

[9] Heo S and Kim J. Double edge trailing PWM based full digital audio amplifier design[C]. Proceedings of 2012 IEEE International Conference on Consumer Electronics, Las Vegas, 2012: 251-252.

[10] Gwee B, Chang J, and Li H. A micropower low-distortion digital pulsewidth modulator for a digital class D amplifier[J].IEEE Transactions on Circuits and System-Ⅱ Analog and Digital Signal Processing, 2002, 49(4): 245-256.

[11] Goldberg J and Sandler M. New high accuracy pulse width modulation based digital-to-analogue convertor/power amplifier[C]. Proceedings of the IEE Circuits, Devices and Systems, London, 1994: 315-324.

[12] Guanziroli F, Bassoli R, Crippa C, et al.. A 1 W 104 dB SNR filter-less fully-digital open-loop class D audio amplifier with EMI reduction[J]. IEEE Journal of Solid-State Circuits, 2012,47(3): 686-698.

[13] 郑杰, 王京梅, 李莉, 等. 基于ILI算法的数字D类放大器调制模块[J]. 电路与系统学报, 2012, 17(5): 26-30.Zheng J, Wang J M, Li L, et al.. ILI-based modulator for digital class-D amplifier[J]. Journal of Circuits and Systems,2012, 17(5): 26-30.

[14] Aase S. A prefilter equalizer for pulse width modulation[J].Signal Processing, 2012, 92(10): 2444-2453.

[15] Yu Z and Feng H. A method of error correction for digital class D power amplifier[C]. Proceedings of 1st Asia Pacific Conference on Postgraduate Research in Microelectronics and Electronics, Shanghai, 2009: 153-156.

[16] Black H. Modulation Theory[M]. New York: Van Nostrand,1953: 263-281.