基于最小区域法的形位公差精确算法

计自飞，丁 拳

（中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

航空发动机是由成千上万的各种零部件组成，因此，其高性能源于优秀设计，更离不开优秀制造工艺的可靠保证。零部件的精密程度将直接影响到发动机的稳定性和可靠性。在发动机的各式零部件中，回转体构件数量众多，且具有特殊的重要作用。因此，对发动机回转体构件的圆度、圆柱度和直线度等的测量分析十分重要。而其准确的测量结果和快速评估对于判定精密回转类零部件的合格与否至关重要。形位公差的评定方法有很多种，其中，最小区域法和最小二乘法适用于每种形位公差的计算。最小二乘法尽管发展较为完善，但是，方法本身存在一些缺陷，而最小区域法是完全符合形位公差定义的评定方法[1-2]。对此，国内外的专家学者已做过很多研究，并提出了一些优化方法，但这些方法有些思路复杂，如遗传算法[3]、仿增量算法[4]等，有些方法对初始条件要求过高，如区域搜索算法[1-5]等，需以最小二乘法的计算结果作为初始条件，且搜索步长难于控制，过小则计算量大，过大则精度不够，因而都不易于在工程领域广泛采用。有些研究者利用MATLAB自带的优化工具箱来实现最小区域法求解圆度误差的问题[6-8]，但使用这种方法需要精通MATLAB软件，推广应用有诸多不便。

本文提出1种基于最小区域法的逐次逼近算法，思路简单，易于编程实现，又很好地克服了最小二乘法的诸多不足，通过编写成fortran程序，编译生成的可执行文件可在任意1台计算机上运行，便于推广应用。

1 最小二乘法的求解过程

最小二乘法求解形位公差的理论发展比较完善，算法简单，因此，得到了广泛应用。根据文献[1]中的推导，其数学模型是非线性的，但如果在测点均匀分布时，计算模型就能转化为线性化模型，而且，根据GB/T1182-2008中对于形位公差的定义，最小二乘法的求解思路不满足最小条件要求，其计算结果与真实形位公差存在差异，这属于评定方法的系统误差。下面简要介绍利用最小二乘法求解形位公差的方法。

1.1 直线度

直线度包括给定方向上的直线度、给定平面内的直线度、空间任意方向上的直线度等3种情况。这里研究给定平面内的直线度。

设（xi,yi）,i=1,2,…，n 为给定平面内的测点坐标。设由最小二乘法求出的理想直线方程为

式中：k、b 为待定参数。

则残余误差为

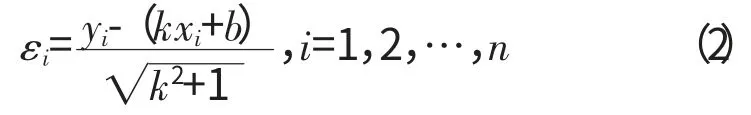
最小二乘法的目标函数为

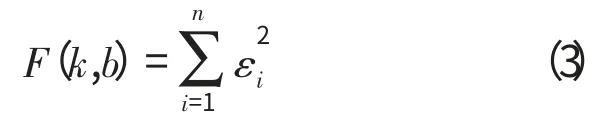
约束条件为

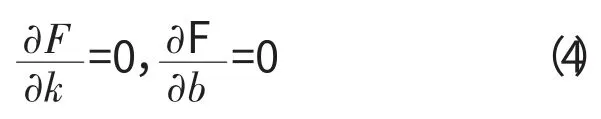
将式（3）带入式（4），化简后求解，得到k、b 的表达式。则直线度误差为

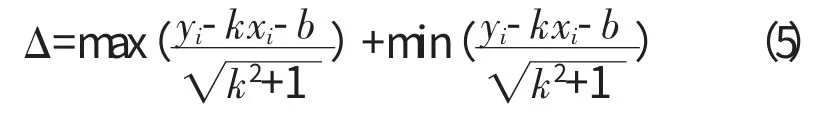
1.2 平面度

设（xi，yi，zi），i=1，2，…，n 为给定的空间测点坐标。设由以上测点拟合出的最小二乘平面方程为

式中：A、B、C 为待定参数。

则残余误差为

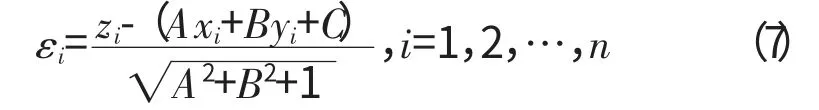
最小二乘法的目标函数为

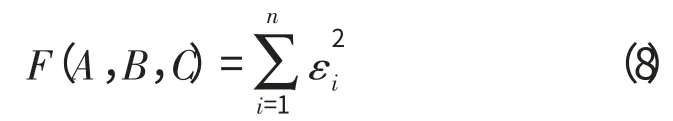
约束条件为

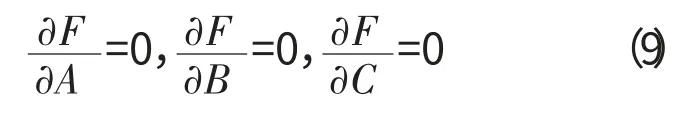
将式（8）带入式（9），化简后可以得到A、B、C 的表达式，从而平面度误差的最小二乘法结果为

1.3 圆度

设（xi,yi,zi）,i=1,2,…，n 为被测圆周上采样点坐标，由以上测点拟合出的最小二乘圆方程为

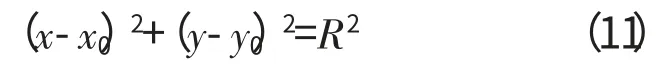
式中：（x0,y0）为最小二乘圆心；R 为最小二乘圆半径。

则残余误差为

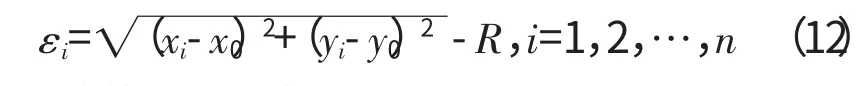
最小二乘法的目标函数为

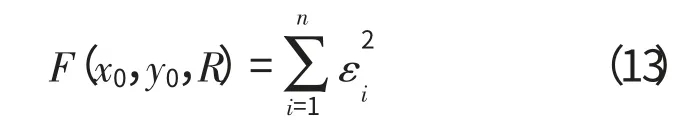
约束条件为

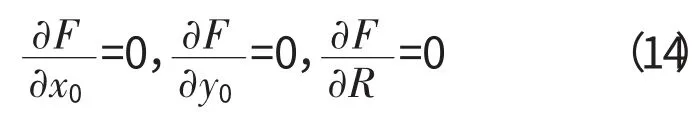
将式（13）带入式（14），化简后可以得到A、B、C的表达式，从而平面度误差的最小二乘法结果为

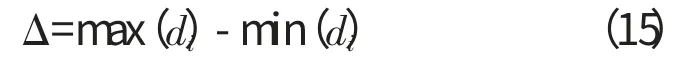
式中：di为各测点到最小二乘圆心的距离。

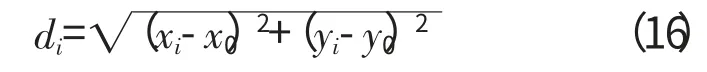
1.4 圆柱度

假设各横向测量截面上测点坐标为（xi,yi,zi）,i=1,2,…，n，设由以上测点拟合出的最小二乘圆柱的半径为R，则轴线方程为

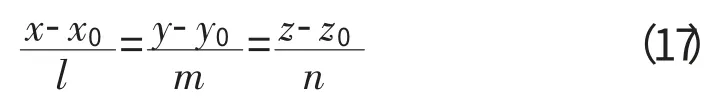
式中：x0、y0、z0、l、m、n、R 为待定参数。

则残余误差为

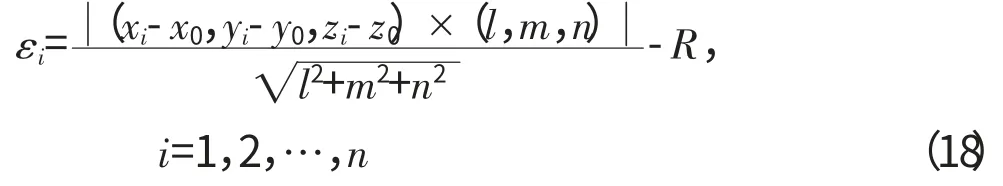
最小二乘法的目标函数为

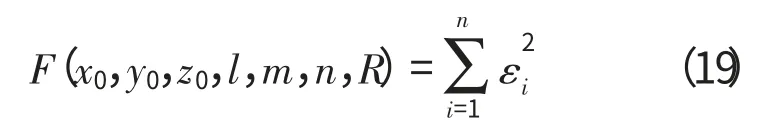
约束条件为

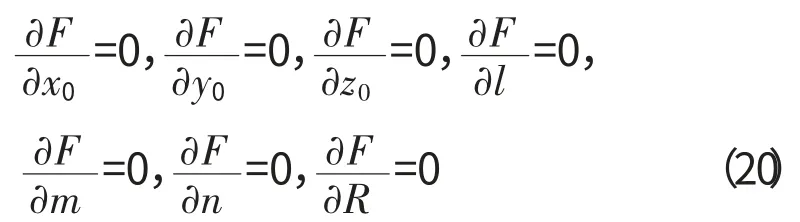
将式（19）带入式（20），化简后可以得到A、B、C的表达式，从而平面度误差的最小二乘法结果为

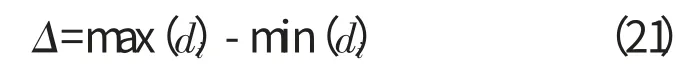
式中：di为各测点到最小二乘圆柱轴线的距离。

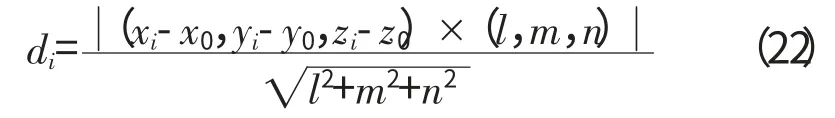
2 基于MATLAB的最小区域法优化的实现方法

MATLAB软件自带的优化工具箱(optimization toolbox)提供了诸如共轭梯度法、单纯法、牛顿法、序列二次规划等局部优化算法，一旦初值合理，收敛速度快，满足约束的精度高。合理利用优化工具箱可以很方便地求解一些有约束或无约束的非线性极小值问题，优化工具箱的GUI界面如图1所示。

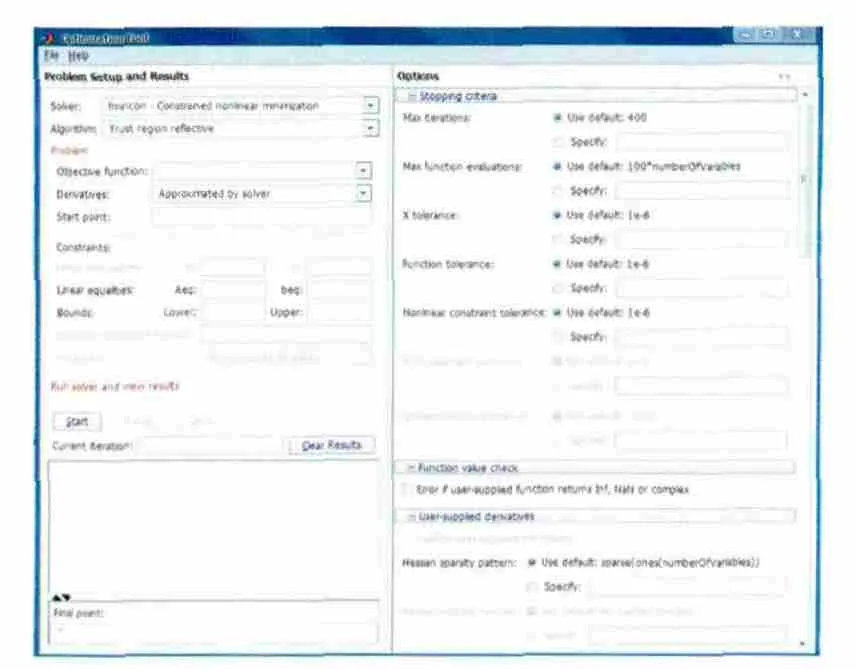
图1 MATLAB优化工具箱GUI界面

基于最小区域法的形位公差评定问题属无约束条件的非线性极小值问题，可用fminunc或fminsearch函数实现[10]，以fminunc函数为例：

[x,fval,exitflag,output]=fminun(fun,x0,options)其中：x 为最优解；fval 为返回目标函数在最优解处的值；exitflag为返回算法终止标志；output为返回优化算法信息的1个数据结构；fun 为目标函数；x0为初始值；options 为设置优化选项参数。

只要将式（5）、（10）、（15）、（21）作为目标函数，即可利用上述方法完成基于最小区域法的形位公差的评定。

3 逐次逼近算法的求解过程

3.1 算法的输入条件

逐次逼近算法，不像区域搜索法那样，要靠最小二乘法的计算结果来确定搜索范围，只需要给出测点数目、采用的测量坐标系、各个测点的坐标即可，将其以固定格式写入txt文件即可，程序运行时可自动获取这些信息。

通过一些简单的语句可以确定测点坐标的大致分布范围，以此确定初次计算域。以圆度计算为例，设xmin，xmax分别为各测点x 坐标的最小、最大值，ymin，ymax分别为各测点y 坐标的最小、最大值，则首次计算域可选为以(xmin，ymin)、(xmin，ymax)、(xmax，ymin)、(xmax，ymax)为顶点的矩形区域。然后将长和宽分别m、n 等分，则计算域内第i 行、j 列的节点坐标为

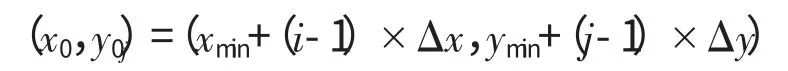
其中

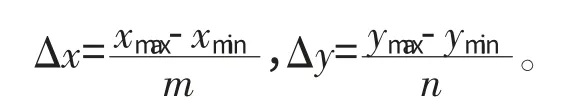
3.2 算法的求解过程

逐步逼近算法的具体实施步骤：

（1）按一定格式编辑测点信息，待程序运行后，根据测点信息确定了待定参数的初次计算域，并将每个优化参数的计算域n 等分。

（2）分别计算当优化参数位于各等分点上时的形位公差值，找出形位公差取最小值时对应的优化参数值。

（3）以上次计算找出的优化参数为中心，重新划分1个较小的计算域，再将每个优化参数的计算域n等分。

（4）再次计算当优化参数分别位于各自等分点上时的形位公差值，找出形位公差取最小值时对应的优化参数值。

（5）重复式（3）～（4），直到计算出的形位公差值与前1次的结果之差小于预定的偏差阈值ε。

将上述逐次逼近算法用于回转零部件的圆度计算，过程如图2所示。（1）根据测点坐标分布范围确定初次计算域；（2）以第1次找出的圆度最小值对应的坐标为中心，重新设定1个较小的计算域；（3）循环n次后，再次缩小计算域后得到的圆度值和圆心位置基本不变。

如上所述，假定每计算1次后就将每个待定参数的计算域减小一半，但等分的份数不变，这样每计算1次，计算步长就缩小1倍，因此，只要循环的次数足够多，就一定能得到准确的形位公差值。为了计算的可靠性，后1次循环的计算域比前1次的计算域不能缩小得太多。其算法流程如图3所示。

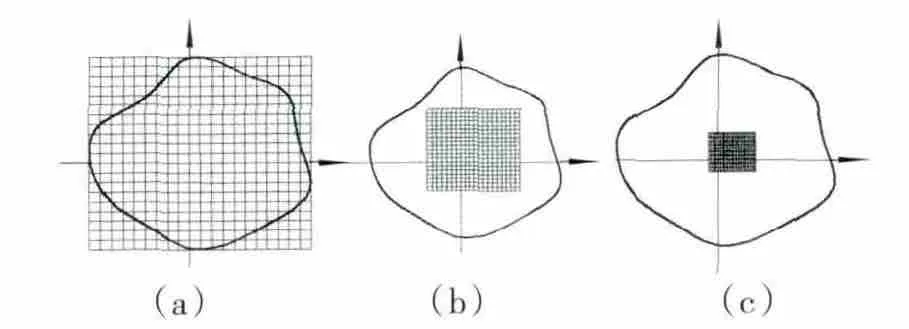
图2 利用逐次逼近算法的圆度计算过程

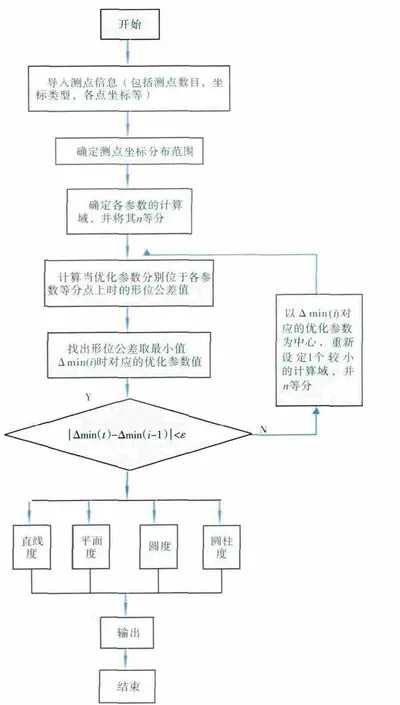
图3 逐次逼近算法流程

4 算法验证

选取直线度和圆度2种形位公差，分别选用最小二乘法、MATLAB优化算法以及逐次逼近算法进行求解，通过对比来验证逐次逼近算法的有效性。

4.1 直线度

1组等间距分布测点的直角坐标值如下：

分别利用3种方法计算得出的直线度误差以及相应的最优解斜率详见表1。

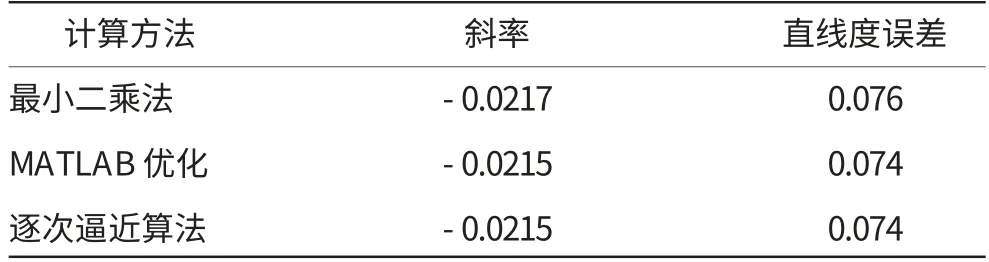
表1 直线度比较

4.2 圆度

对于下面1组周向均布的极坐标下的测点数据[41.0532,41.0527,41.0536,41.0072,41.0065,40.9982,41.0526,41.0538,40.9973,41.0026,40.9957,41.0546,41.0549,40.9995,40.9969,41.0439]，分别利用3种方法计算圆度和位置度偏差，见表2。

表2 圆度比较

4.3 分析

通过对比3种不同方法对直线度和圆度误差的评定结果，可见最小二乘法的评定结果不满足最小条件要求。除圆心坐标外，逐次逼近算法的评定结果与MATLAB优化结果一致，这是因为最小区域法求出的圆心不惟一，但圆度误差值惟一。MATLAB作为成熟的商业软件，其优化结果相对稳定，逐次逼近算法的计算结果与之一致，证明了该算法的有效性。

5 总结

（1）逐次逼近算法思路简单，易于编程实现，初始计算条件简单，并克服了最小二乘法的诸多不足，且无需特殊运行环境。

（2）通过与其他方法计算结果对比说明，逐次逼近算法可以精确高效地完成形位公差的评定，计算结果好于最小二乘法，符合最小条件要求。

（3）逐次逼近算法简单易行，计算正确有效，值得在工程实践中应用和推广。

[1]黄富贵，郑育军.基于区域搜索的圆度误差评定方法[J].计量学报，2008，29（2）：117-119.HUANG Fugui，ZHENG Yujun.A method for roundness error evaluation based on area hunting[J].Acta Metrologica Sinica，2008，29（2）：117-119.（in Chinese）

[2]全国产品尺寸和几何技术规范标准化技术委员会.GB/T 1182-2008产品几何技术规范(GPS)几何公差形状、方向、位置和跳动公差标注[S].北京：中国标准出版社，2008：1-48.National Technical Committee on Product Dimension and Geometric Element Specifications of Standardization Administration of China.GB/T 1182-2008 Geometrical Product Specifications(GPS)—geometrical tolerancing—tolerances of form，orientation，location and run-out[S].Beijing：China Standard Press，2008：1-48.（in Chinese）

[3]Cui Changcai，Che Rensheng，Ye Dong.Circularity error or evaluation using genetic algorithm [J].Optics and Pricision Engineering，2001，9（6）：499-505.

[4]岳武陵，吴勇.基于仿增量算法的圆度误差快速准确评定[J].机械工程学报，2008，44（1）：87-91.YUE Wuling，WU Yong.Fast and accurate evaluation of the roundness error based on quasi-incremental algorithm[J].Chinese Journal of Mechanical of Engineering，2008，44（1）：87-91.（in Chinese）

[5]田树耀，黄富贵，张彬.一种基于区域搜索的平面度误差评定方法 [J].华侨大学学报：自然科学版，2009，30（5）：506-508.TIAN Shuyao，HUANG Fugui，ZHANG Bin.An evaluation method for flatness error based on region searching[J].Journal of Huaqiao University：Natural Science，2009，30（5）：506-508.（in Chinese）

[6]张小萍，王君泽.基于测点分类的圆度误差精确评定[J].机械设计与制造，2010（9）：166-167.ZHANG Xiaoping，WANG Junze.Accurate evaluation of roundness error by classifying measured points[J].Machinery Design&Manufacture，2010（9）：166-167.（in Chinese）

[7]刘国光.基于MATLAB评定圆柱度误差[J].工程设计学报，2005，12（4）：236-239.LIU Guoguang.Cylindricity error evaluation based on MATLAB [J].Journal of Engineering Design，2005，12（4）：236-239.（in Chinese）

[8]周建平.基于MATLAB的圆度评定方法 [J].计量与测试技术，2005，32（2）：5-7.ZHOU Jianping.The method of roundness assessment based on MATLAB[J].Metrology&Measurement Technique，2005，32（2）：5-7.(in Chinese)

[9]全国产品尺寸和几何技术规范标准化技术委员会.GB/T 7235-2004产品几何技术规范(GPS)评定圆度误差的方法半径变化量测量[S].北京：中国标准出版社，2005：1-18.National Technical Committee on Product Dimension and Geometric Element Specifications of Standardization Administration of China.GB/T 7235-2004，Geometrical Product Specifications(GPS)—methods for the assessment of departure from roundness—measurement of variations in radius[S].Beijing：China Standard Press，2005：1-18.(in Chinese)

[10]刘国光.基于MATLAB评定圆柱度误差[J].工程设计学报，2005，12（4）：236-239.LIU Guoguang.Cylindricity error evaluation based on MATLAB [J].Journal of Engineering Design，2005，12（4）：236-239.(in Chinese)

[11]周建平.基于MATLAB的圆度评定方法[J].计量与测试技术，2005，32（2）：5-7.ZHOU Jianping.The method of toundness assessment based on MATLAB [J].Metrology& Measurement Technique，2005，32（2）：5-7.(in Chinese)

[12]龚纯，王正林.精通MATLAB最优化计算[M].北京：清华大学出版社，2009：169-171.GONG Chun，WANG Zhenglin.Proficient in MATLAB optimization calculation[M].Beijing:Tsinghua University Press，2009：169-171.(in Chinese)

[13]栾艳华.某型航空发动机机匣同轴度测量[J].航空发动机，2012，38（1）：44-46.LUAN Yanhua.Casing coaxiality measurement for an aeroengine[J].Aeroengine，2012，38（1）：44-46.(in Chinese)

[14]谢海峰.圆度误差测量中的多尺度算法研究[D].长春：吉林大学，2009.XIE Haifeng.Research on the multi-scale slgorithm used in measurement of roundness error[D].Changchun：Jilin University，2009.(in Chinese)