基于蒙特卡罗法的航空发动机稳态空气系统网络计算

胡肖肖，李育隆，吴 宏

（1.中国舰船研究设计中心，武汉430064；2.清华大学航天航空学院，北京100084；3.北京航空航天大学能源与动力工程学院，北京100191）

0 引言

在航空发动机空气系统设计中，稳态空气系统的参数值作为空气冷却系统设计中直接参考的关键参数，关系到空气系统设计是否有效和发动机能否安全可靠地工作，有着重要的研究价值。复杂的空气系统的影响因素较多，几乎不可能对其进行严格的几何求解。但可将稳态下空气在二次空气系统内的流动简单看作1维不可压缩流动，并离散为由不同元件和节点组成的网络系统[1-2]，进而开展计算。目前，在稳态空气系统的计算研究中，常使用流体网络法[3-6]，即数值求解网络系统的连续性方程组和能量方程组。流体网络算法相对成熟，但求解过程是否收敛、收敛速度及计算精度在很大程度上依赖于研究人员的求解经验，并且在求解复杂网络和复杂部件时难以获得收敛解。目前，空气系统稳态算法主要用于航空发动机典型设计点状态的计算。

经过文献调研发现，流体网络的研究不仅存在于航空发动机空气系统领域，在市政管网领域也有对供水及供燃气管网中1维不可压缩稳态流动的研究，其中蒙特卡罗法的应用引起了研究人员关注。例如，吉庆丰等[7]将蒙特卡罗法应用于供水管网分析，建立了相应的随机游动模型，结果表明：蒙特卡罗法计算简便、灵活，所需计算机内存少，便于对多水源的复杂管网进行水力计算。白建辉等[8]为求解天然气管网节点的数学模型方程组，将蒙特卡罗方法的计算结果作为牛顿法节点压力的初始值，高效率地实现了天然气管网稳态分析。结果表明：对于同一算例，用改进算法的计算效率比使用单一算法的明显提高。

为了解决目前稳态空气系统算法在求解复杂网络时不容易获得收敛解的问题，本文尝试引入蒙特卡罗方法[9-10]对航空发动机稳态空气系统网络进行计算，并用商业软件flowmaster验证了计算结果的可靠性。为航空发动机稳态空气系统网络计算提供了1种新方法，并为进一步研究及应用提供了参考。

1 计算方程及方法

1.1 方法原理

蒙特卡罗方法亦称为随机模拟[10]，基本思想是建立1个概率模型或随机过程，使其参数等于问题的解。通过对模型/过程的观察或抽样试验来计算所求参数的统计特征，最后给出解的近似值。本文以概率的思想表示流量的分配关系，通过模拟大量粒子的不断迁移来实现系统内的压力分配，从而求出空气系统内节点的压力，再计算流经各元件的流量。

1.2 基本方程

计算航空发动机空气系统时，依据气体动力学和传热学基础理论，一般将冷却空气系统抽象为由节流单元与腔室组成的流体网络。对于计算中的流热耦合[11-13]（大多是弱耦合[14]），可将温度作为已知条件，分别求解流体网络和热网络。

现采用蒙特卡罗法求解温度条件已知的流体网络。定义空气系统内任一节点m 处流进节点的流量为正，流出节点的流量为负，则节点处质量流量总和为0。连续性方程为

式中：mk为第k 段流动分支的流量。能量方程为

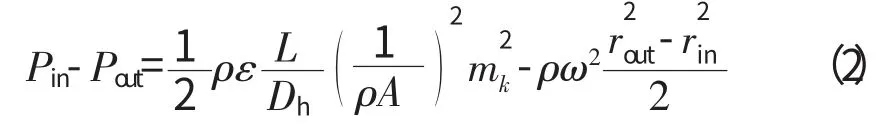
式中：Pin和Pout分别为第k 段分支两端节点处进、出口压力；ρ 为管内流动介质的密度；L、Dh、A 分别为管段的长度、直径、横截面积；ε 为管段的阻力系数（ε 的大小与雷诺数和粗糙度有关）；ω 为旋转角速度；rin、rout分别为进、出口半径。

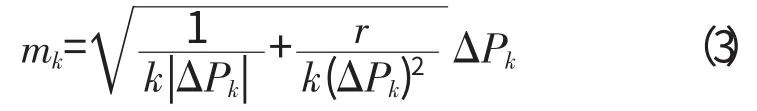
简单流体网络如图1所示，设节点Q1是流体网络中任意1个节点，与之相连的分支管路有n个，相邻的n个节点分别表示为Q11、Q12、…Q1n。

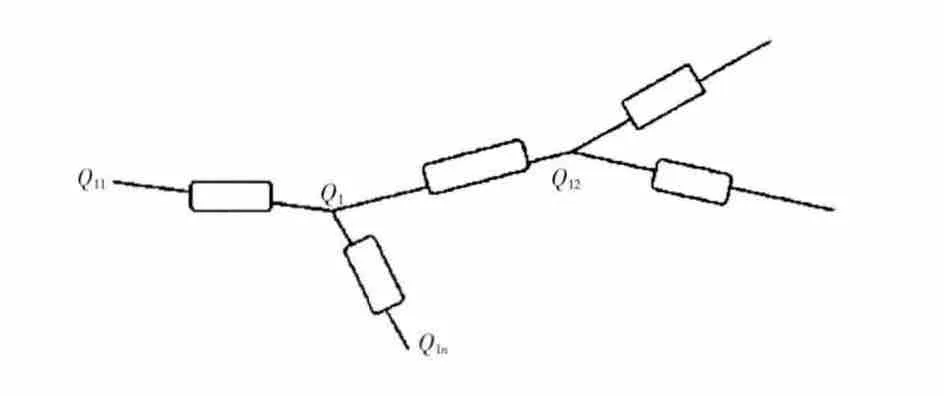
图1 简单流体网络

联立式（1）和式（3），可以化简得节点Q1处压力P（Q1）的方程为

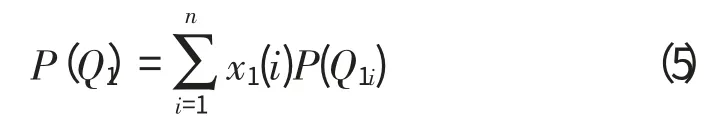
1.3 计算方法

求解空气系统问题即根据系统的流阻特性和几何特性，对空气系统进行流量分配和压力分配。把流体看作大量粒子组成的集合体，粒子从进口依次经过不同节点流至出口，遇到分叉处，粒子以不同的比例分别流入下游各节点。这个过程可以用概率的思想描述为：粒子以一定的概率迁移到相邻节点，不断迁移直至移动到压力已知点，从而实现全场的压力分配。其中，概率的大小由节点间元件的属性决定，也就是式（5）中的转移概率。

引入蒙特卡罗方法进行求解，求解过程为：构造随机游动模型，进行大量重复试验，可以得到不同的试验值，取其平均值作为待求节点的压力值，具体用Fortran语言编程实现。例如求解空气系统网络的某一节点Q1的压力值时，构造以下随机游动模型：某个粒子自Q1节点开始游动，按照转移概率x1（i）向与Q1节点相邻的节点随机移动一步，若粒子第一步到达的节点是Q1m，再按转移概率x1m（i）向与Q1m节点相邻的节点随机移动一步，如此重复下去，直至粒子迁移到压力已知节点结束。假设共有N个粒子进行N 次随机移动，就会获得N个随机变量值ε1，ε2，…εN，其平均值便可作为P（Q1）的近似值[15]。

2 计算算例与分析

2.1 计算算例

以如图2所示的某空气系统网络为例，元件1与进口相连，进口处压力为P1，元件6、10、17分别与3个出口相连，出口压力分别为P7、P11、P18。图中将不同的元件进行编号，已知流体进、出口的压力值，求旋转状态下空气系统中各节点的压力值。

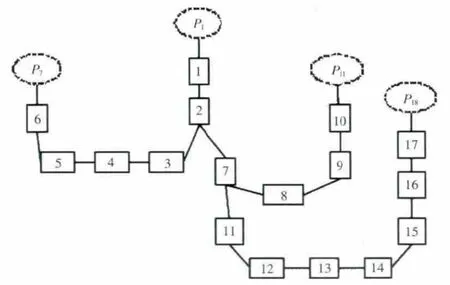
图2 某空气系统网络

空气系统内包含不同的元件，如不同形式的管、封严壁齿、小孔、腔等。为验证蒙特卡罗方法的可行性，把所有元件都当作阻力元件，只要给定阻力系数的值，就可以确定压力和流量的关系。

管道、孔、腔室满足式（2），可将其转化为如式（4）所示的压力和流量的线性关系式。

对于封严篦齿结构

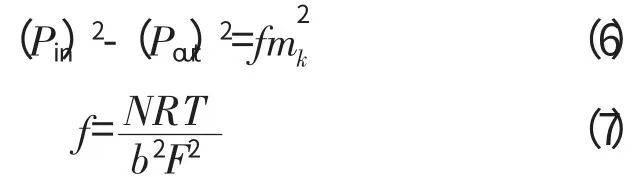
式中：N 为篦齿齿数；F 为侧面积；b 为经验系数；R 为理想气体常数；T 为温度。将封严篦齿公式化为线性形式

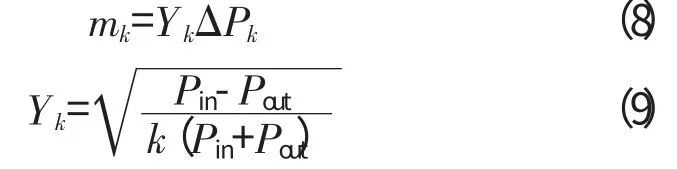
旋转阻力系数为

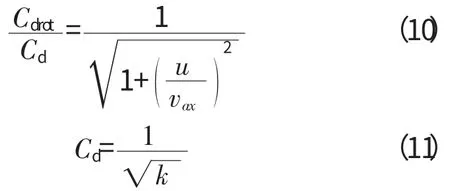
式中：u 为旋转切速度；vax为孔口的轴向流速；Cd为流量系数；Cdrot为旋转阻力系数；k 为阻力系数。

2.2 计算结果与分析

分别设定3组不同工况，即不同的进出口压力与旋转速度，计算得到空气系统各节点的压力，3组工况及计算结果如下：

（1）工况1：T=419.2K，P1=52619Pa，P7=52093Pa，P11=49408Pa，P18=20332Pa，n=0r/min。节点的压力计算结果如图3（a）所示。

（2）工况2：T=435.0K，P1=57488Pa，P7=56913Pa，P11=54718Pa，P18=22295Pa，n=20900r/min。节点压力计算结果如图3（b）所示。

（3）工况3：T=450.2K，P1=62077Pa，P7=61457Pa，P11=58434Pa，P18=24348Pa，n=22000r/min。节点压力计算结果如图3（c）所示。

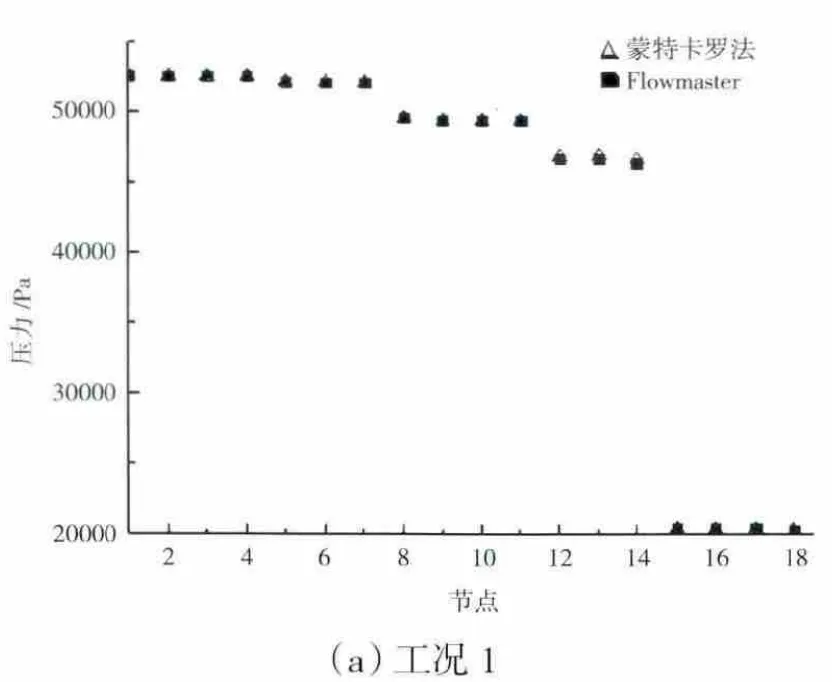
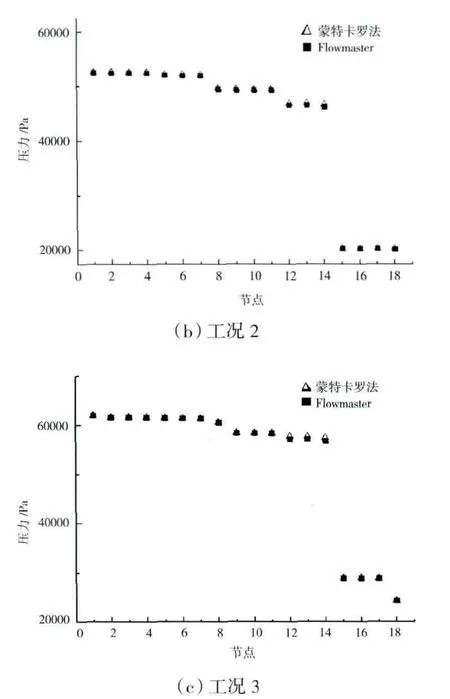
图3 蒙特卡罗法与flowmaster压力计算结果比较

蒙特卡罗方法通过大量的简单重复抽样进行计算，程序简单，不会出现不收敛的情况。计算发现，经过较少次游动，所得的压力值已经比较接近真实值。

从图3中可见，采用蒙特卡罗方法得到的空气系统的各节点压力值与参考结果相差较小，最大误差仅为0.628%。准确的压力计算可为空气系统设计提供重要依据，运用蒙特卡罗方法求得各节点的压力值后，再根据流量与元件两端压力值的关系，计算流经各元件的流体流量。

在工况1条件下，根据如图3（a）所示的压力值计算出流经各元件的流量值，如图4所示。从图4中可见，流经各元件的流量与flowmaster的结果基本一致，但流经元件12、15的流量与flowmaster计算结果有较大误差，最大为0.00367kg/s。这是由于蒙特卡罗方法是随机算法，其收敛是概率意义下的收敛,不能解决精确度要求较高的问题。在计算过程中，以压力为控制变量，经过不断迭代，得出误差较小的压力值，但无法避免误差。由于压力变化会引起较大的流量变化，因此流量计算结果也会有一定误差。

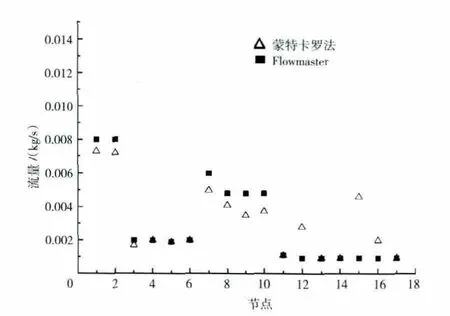
图4 蒙特卡罗法与flowmaster流量计算结果比较

3 结论

通过大量的简单重复抽样可实现运用蒙特卡罗方法求解稳态空气系统，该方法思路清晰、使用简便，对初值的设定不敏感，不会出现无法求解复杂空气系统的情况。在求解过程中发现，经过数次游动即可得到比较接近压力值的解。用flowmaster软件对该计算方法进行验证，压力计算结果最大偏差为0.628%，说明2种方法的计算结果吻合较好，也初步验证了蒙特卡罗方法求解航空发动机稳态空气系统网络的可行性。

根据压力值计算出的流量有一定误差，结合其他方法（如牛顿-拉夫逊法），有可能提高计算精度，这需要进一步研究优化。

[1]陆海鹰，杨燕生，王鸣.航空发动机空气系统特性的数值模拟[J].航空发动机，1997（1）：6-13.LU Haiying,YANG Yansheng,WANG Ming.The numerical simulation of the aeroengine air system [J].Aeroengine,1997（1）:6-13.(in Chinese)

[2]左承基，傅秋阳，欧阳明高，等.压缩空气发动机系统的数值模拟[J].合肥工业大学学报：自然科学版，2005，28（9）：985-988.ZUO Chengji,FU Qiuyang,OUYANG Minggao,et al.Numerical simulation of the compressed air engine system[J].Journal of Hefei University of Technology:Natural Science,2005,28（9）:985-988.(in Chinese)

[3]Majumdar A,Steadman T.Numerical modeling of pressurization of a propellant tank[J].Journal of Propulsion and Power,2001,17(2):385-390.

[4]Kritpiphat W,Tontiwachwuthikul P,Chan C.W.Pipeline network modeling and simulation for intelligent monitoring and control:a case study of a municipal water supply system[J].Industrial&Engineering Chemistry Research,1998,37(3):1033-1044.

[5]Obradovic D.Modelling of demand and losses in reallife water distribution systems[J].Urban Water,2000,2(2):131-139.

[6]陶智，侯升平，韩树军，等.流体网络法在发动机空气冷却系统设计中的应用[J].航空动力学报，2009，24（1）：1-6.TAO Zhi,HOU Shengping,HAN Shujun,et al.Study on application of fluid network into the design of air system in engine[J].Journal of Aerospace Power,2009，24（1）:1-6.(in Chinese)

[7]吉庆丰，周济人.应用蒙特卡罗法分析供水管网[J].灌溉排水，1998，17（4）：16-20.JI Qingfeng,ZHOU Jiren.Pipe network analysis with Monte Carlo method[J].Irrigation and Drainage,1998,17（4）:16-20.(in Chinese)

[8]白建辉，汪玉春，郜峰，等.天然气管网稳态分析综合方法[J].油气储运，2009，28（2）：37-39.BAI Jianhui,WANG Yuchun,GAO Feng,et al.Combination based algorithm for steady analysis of natural gas pipeline network[J].Qil&Gas Storage and Transportation,2009,28（2）:37-39.(in Chinese)

[9]徐钟济.蒙特卡罗方法[M].上海：上海科学技术出版社，1985：2-18.XU Zhongji.Monte Carlo method[M].Shanghai:Shanghai scientific&Technical Publishers,1985：2-18.(in Chinese)

[10]朱本仁.蒙特卡洛方法引论[M].济南：山东大学出版社，1987：30-42.ZHU Benren.Introduce of Monte Carlo method[M].Jinan:Shandong University Press,1987：30-42.(in Chinese)

[11]朱惠人，白洛林，张丽，等.多孔隔热壁温度场气动传热耦合计算方法[J].航空动力学报，2003，18（2）：230-234.ZHU Huiren,BAI Luolin,ZHANG Li,et al.Coupled method of flowheat transfer to calculate temperature field of multihole wall[J].Journal of Aerospace Power,2003,18（2）:230-234.(in Chinese)

[12]Miltiadis V P.Feed back control of thermal systems modeled via the network approach[J].Journal of Dynamic Systems,Measurement,and Control,2004,126（3）:509-519.

[13]Athavale M M,Ho Y H.Analysis of coupled seals,secondary and power stream flow fields in aircraft and aerospace turbomachines[R].NASA-CR-2005-212716.

[14]吴丽君，吴宏.流热网络耦合及局部3维计算方法研究[J].科学技术与工程，2011，11（3）：521-527.WU Lijun,WU Hong.Study of thermal flow network and local three dimensional calculation method[J].Science Technology and Engineering,2011,11（3）:521-527.(in Chinese)

[15]Spiegel M R,Schiller J J,Srinivasan R A.Probability and statistics[M].New York:McGraw-Hill,2009：23-74.