粒子群混合算法在变导向器面积计算中的应用

王 军，赵 肃

（中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

目前，航空发动机高精度稳态数学模型均按变比热计算方法[1]建立，具有高度非线性、基于部件特性的特点。模型一般采用迭代方法求解发动机共同工作方程，常用的迭代方法有Newton-Raphson（N-R）法、Broyden秩1法[2]、N+1点残量法[3]和最速下降法，上述方法具有严格的数理局部收敛性，且收敛性依赖初值的选取，虽通过采用阻尼因子、松弛因子、初值的有限域优化探索和迭代步长的线性探索与回溯[4]等改进方法可扩大其收敛范围，但一般改善程度都较小；鉴于发动机工作包线宽广及在特殊工作条件（如几何面积突变等）下，发动机各部件共同工作时，因初值偏离最优解较大导致模型出现不收敛的情况。

为了克服上述算法在收敛性方面的不足，粒子群算法（ParticleSwarmOptimization，PSO）等进化算法被引入发动机部件模型等非线性方程的求解[5-6]中，取得了较好效果。PSO具有全局收敛的能力，在进化初期收敛速度快，运算简单，易于实现，但其计算效率和收敛精度偏低，同时存在最优解不稳定的问题。结合常规迭代算法计算效率高和PSO全局收敛的优点的混合算法改善了发动机部件模型求解过程中的收敛性。

本文采用混合粒子群算法解决在改变发动机涡轮导向器面积对性能影响计算中迭代不收敛的问题，以满足稳态性能仿真的需要。

1 粒子群算法及其改进

1.1 基本的粒子群算法

基本的粒子群算法[7]以模拟鸟的群体智能为特征，以求解优化问题为背景。每只鸟被称为1个粒子，每个粒子用其几何位置和速度向量表示，参考各自的既定方向、个体所经历的最优方向和整个鸟群所经历的最优方向来确定飞行。假设在1个D 维的目标探索空间中有n个粒子，其中第i个粒子表示为1个D 维的向量，xi=（xi1，xi2，…，xiD）（i=1，2，…，n），表示第i个粒子在此探索空间中的位置，vi=（vi1，vi2，…，viD），表示第i个粒子的速度。假设第i个粒子迄今为止探索到的最优位置为pi=（pi1，pi2，…，piD），整个粒子群迄今为止探索到的最优位置为pg=（pg1，pg2，…，pgD），采用下列公式对粒子群进行速度和位置更新

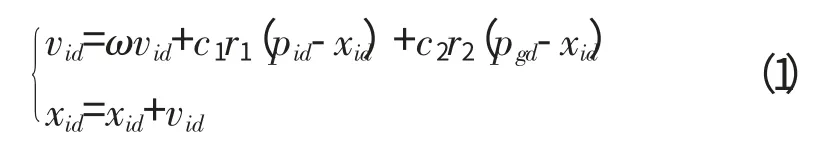
式中：i=1，2，…，n，d=1，2，…，D；c1，c2为非负常数的学习因子；r1，r2为 [0,1]间的随机数；vid=[vmin，vmax]，vmin/vmax为更新速度的最大/最小边界；ω 为惯性权重。

1.2 改进的粒子群算法

在基本粒子群算法的基础上，为提高粒子全局探索能力，发展了带“被动聚集压力”因子的PSO、自适应惯性权重的PSO[8]、混合探索粒子群算法（MSPSO）[9]及加速收敛的PSO（ACPSO）[10]等。

带“被动聚集压力”因子的PSO

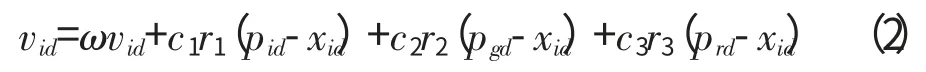
式中：c3为被动聚集压力因子；Prd为粒子群中随机选择的1个粒子；r3为[0,1]间的随机数。

自适应惯性权重的PSO

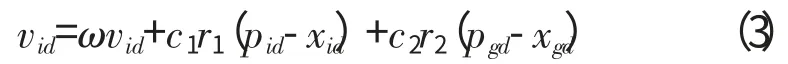
式中:ωi为惯性权重，根据适应度函数值或者迭代次数自动调整。

混合探索粒子群算法（MSPSO）

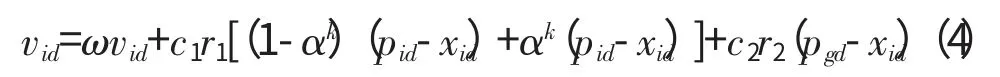
式中：α 为[0,1]之间的1个常数；k 为迭代次数；Pld是第k 代种群中粒子最好位置。

加速收敛的PSO算法（ACPSO）

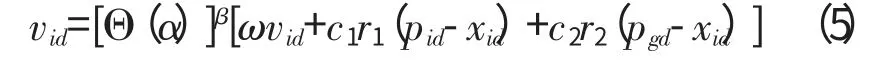
式中:Θ 为三角函数算子，一般取Θ=sin；α 为角度值，一般取α∈[0，π/8]；β 为大于零的常数，一般取β=3。

目前对PSO的改进主要集中在算法参数和粒子更新结构的调整上，目的是使粒子跳出局部最优，使其全局和局部探索能力达到最佳平衡，提高算法的性能。但从航空发动机部件模型求解实例来看，因部件模型高度非线性化，导致模型的收敛速度和精度均低于传统N-R等算法的收敛速度和精度，为进一步提高模型的收敛效率，在上述研究基础上发展了粒子群混合算法。

1.3 粒子群混合算法

为综合传统算法和粒子群算法的优点，提出了PSO-NR（粒子群-牛顿拉夫逊）和PSO-N+1（粒子群-N+1点残量法）[11]等混合算法。

以PSO-NR混合算法为例说明混合算法的工作原理：在该算法中，N-R法仍为求解发动机部件非线性模型的主体算法，在性能计算时对在设定循环迭代次数内不收敛的工作点采用PSO算法，变量初值采用N-R法最后1次循环获得的数值。当循环迭代次数达到设定值后（根据计算精度设置合适的迭代次数），再次采用N-R法进行迭代计算，达到后期快速收敛的目的。如果计算仍不收敛，考虑到PSO获得的最优解不稳定，再次采用混合算法，使用次数一般不大于10次，以免陷入死循环。

2 应用粒子群混合算法求解发动机部件模型

2.1 发动机部件模型的建立

以某型军用混合排气涡扇发动机为研究对象，按照输入的控制规律和变量初值及部件间遵循的流量、压力和功率平衡原则建立发动机共同工作方程[12]，并将其转换为误差方程（残差方程）

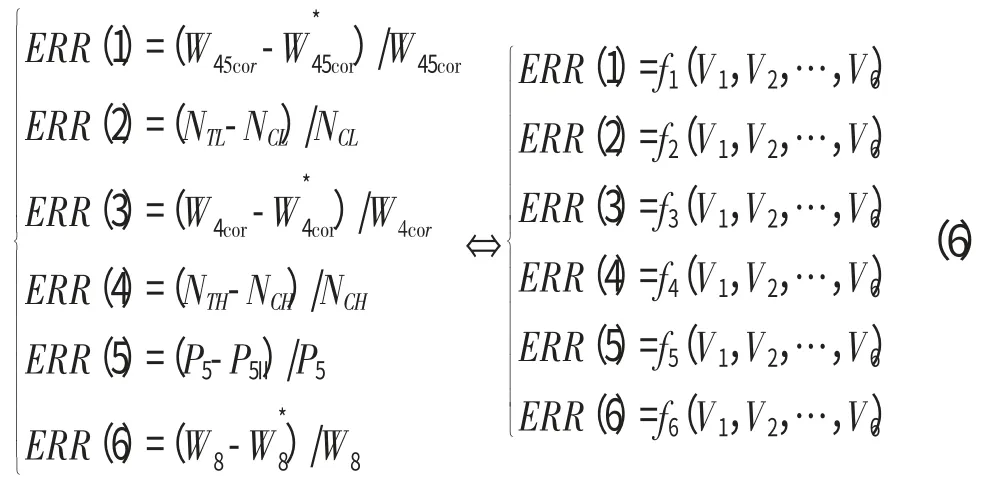
PSO是1种优化算法，采用PSO求解非线性方程组，需要将方程组的求解问题转化为函数的优化问题。应用无约束优化方法求解非线性方程组（式（6））时，通常将其转化为非线性最小二乘问题：

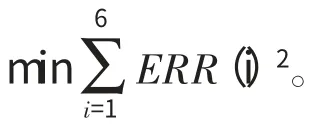
2.2 粒子群混合算法参数的设置

2.2.1 学习因子

对于学习因子c1和c2，关系到个体最优与全局最优对粒子的影响程度。数学研究显示，c1+c2>4且c1>c2时收敛性较好。学习因子对收敛性影响对比如图1所示，采用文献[10]中3组取值求解部件模型的收敛情况。

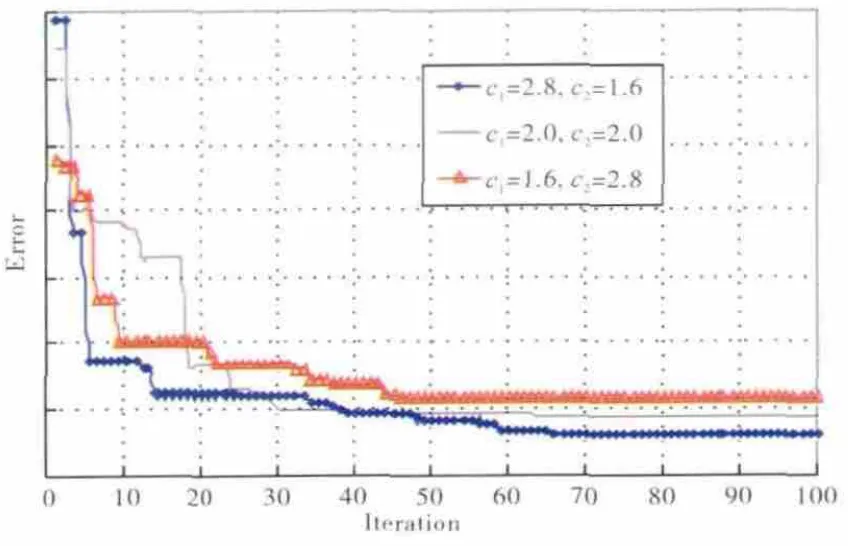
图1 学习因子对收敛性影响对比

2.2.2 惯性权重

随着迭代次数的增加，最优解的探索范围将逐渐缩小，对于惯性权重，变惯性权重的收敛效果要比定惯性权重的好。1种方法采用递减函数[10]来保证算法不会因粒子运动惯性过大而造成收敛缓慢，另1种方法是惯性权重随着粒子适应度的变化而变化，适应度值增大惯性权重也增大，反之随其减小而减小。

前者ω 函数定义为

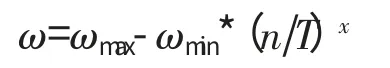
式中：ωmax、ωmin分别为惯性权重的上、下限；T 为迭代总次数；n 为当前迭代次数；x 为函数的凸凹形态。

后者ω 函数定义为

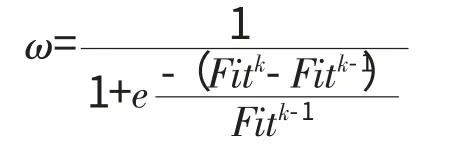
式中：Fitk为某个粒子第k 次迭代时的适应度值。

对于所研究的部件模型，2种变惯性权重方法的收敛性对比如图2所示。从图中可见，以适应度值为自变量的惯性权重的收敛速度更快、收敛精度更高。

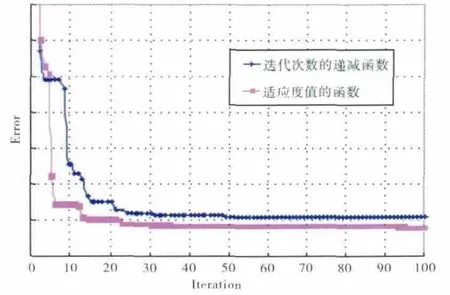
图2 惯性权重对收敛性影响对比

2.2.3 局部改进的PSO

利用第2.1节建立的发动机部件模型，测试基本PSO、带“被动聚集压力”因子的PSO、MSPSO和ACPSO等粒子群算法的收敛性，结果如图3所示。从图中可见，3 种改进的PSO收敛速度较基本PSO的快，收敛精度差别不大，本文采用混合探索粒子群算法（MSPSO）。

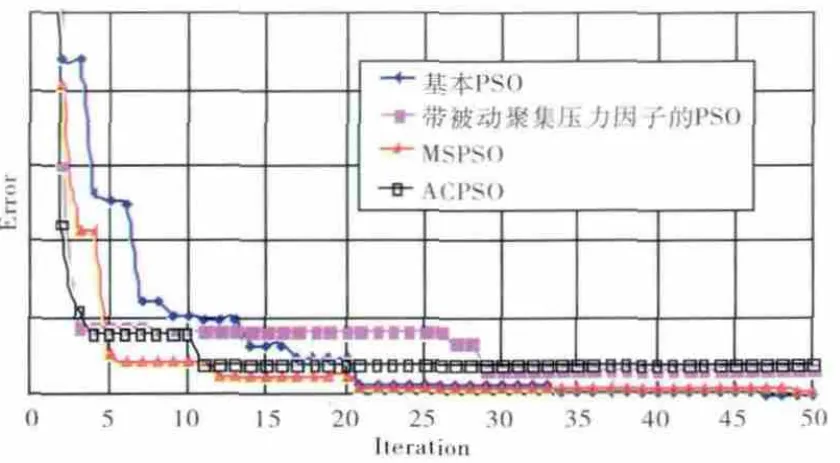
图3 局部改进方法对收敛性影响对比

2.2.4 迭代误差限

对于粒子群混合算法，需设置2个迭代误差限，即PSO和N-R 算法的迭代误差限。在一般情况下，PSO的误差限要大于N-R 算法的，主要因为PSO后段收敛缓慢，较小的误差限会导致迭代次数增加，计算效率下降，PSO的误差限可取收敛曲线的拐点。N-R 算法的计算精度较高，可以取目标误差限作为其误差限。本文PSO的误差限取0.03，N-R 算法的误差限取0.003。

3 变导向器面积计算实例与试验验证

一般来说，实际发动机很难完全满足设计要求，这就需要发动机在调试阶段为满足性能匹配和优化的要求，具备一定的调整能力。主要体现在风扇、压气机可调角度的优化，以及涡轮导向器排气面积、喷管喉道面积的微调上。压气机可调叶片角度及喷管喉道面积一般为发动机控制参数，其调节规律易于实现。涡轮导向器在固定涵道比的发动机上是不可调的，为了满足性能优化需求，需要生产不同组别的涡轮导向器供试验用，费用高、周期长。利用数值仿真可在发动机生产之前确定生产组别的数量和大小，指导调试方向，减少试制和试验费用。

现有的发动机稳态数学模型大多采用经典的N-R 算法，在进行涡轮导向器面积变化对发动机性能影响计算时，因特性图或折合流量差别较大，导致误差突变，出现迭代不收敛的现象，采用PSO-NR 算法能够很好地解决。

3.1 高压涡轮导向器面积变化

在调整某型发动机高压涡轮导向器面积的计算时，可采用小偏差流量不变或更换部件特性的方法。前者主要考虑在慢车转速以上，高压涡轮导向器处于临界状态，导向器面积的变化可以认为只是流过涡轮的折合流量的变化，且忽略涡轮效率变化的影响，在一定条件下能够满足精度需要；后者的计算精度较高，但需要部件提供精确的计算或试验修正特性。

在上述计算条件下，采用PSO-NR 算法计算高压涡轮导向器相对于基准值偏小3.5%对转差、低压涡轮出口排气温度T6和推力F 的影响，其计算和试验结果的对比如图4～6所示。

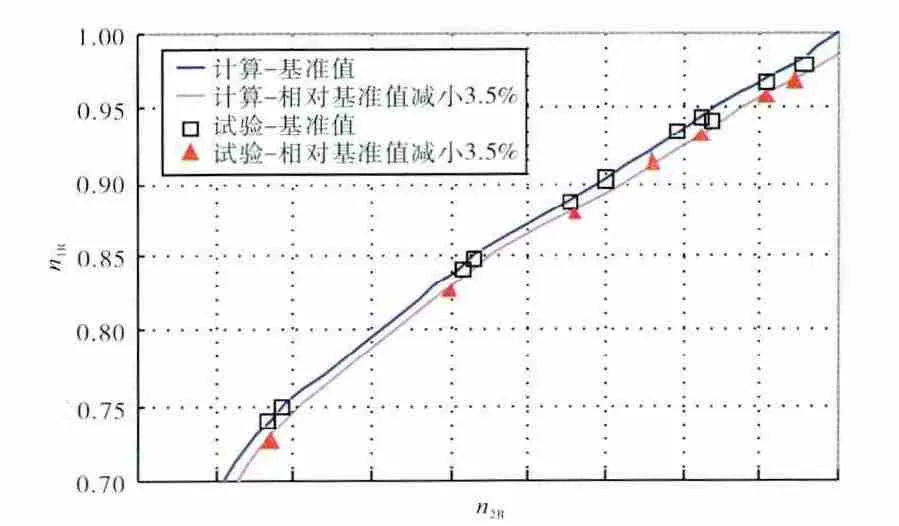
图4 高压涡轮导向器面积变化对转差的影响

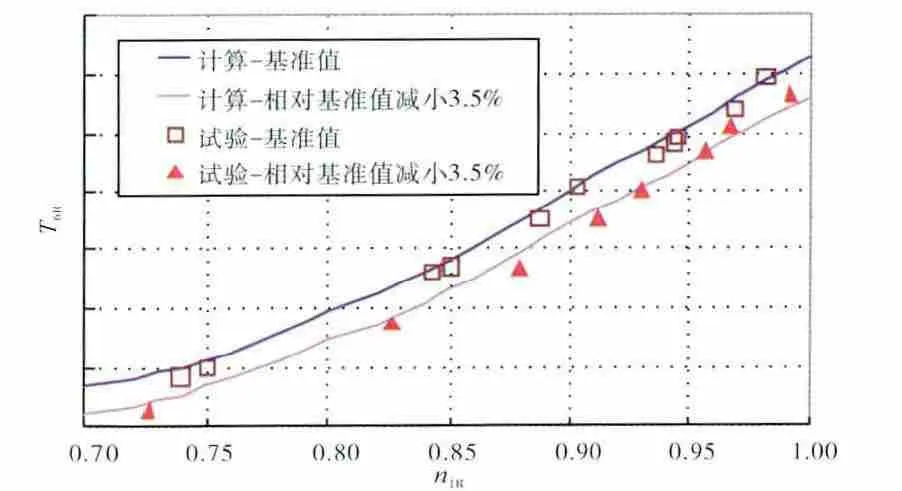
图5 高压涡轮导向器面积变化对排气温度的影响

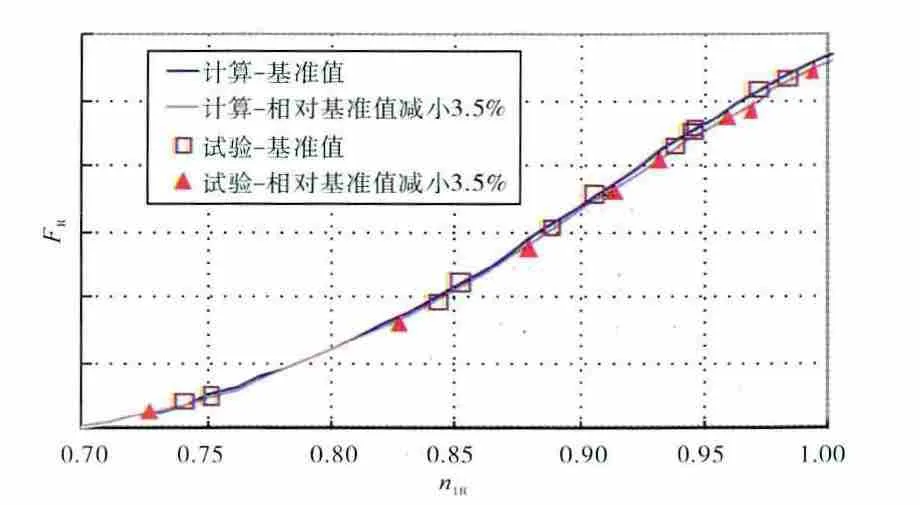
图6 高压涡轮导向器面积变化对推力的影响

从图中可见，当高压涡轮导向器面积减小3.5%时，发动机转差增大0.6%～1.0%，排气温度降低10～15K，推力减小1.2%～1.9%。

3.2 低压涡轮导向器面积变化

在进行调整某型发动机低压涡轮导向器面积的计算时，考虑到低压涡轮导向器仅在高转速范围内才能处于临界状态，采用更换部件特性的方法计算全转速特性。计算低压涡轮导向器相对基准值增大4%对转差、低压涡轮出口排气温度T6和推力F 的影响，其计算和试验结果的对比如图7～9所示。

从图中可见，当低压涡轮导向器面积增加4%时，发动机转差增大0.5%～0.7%，排气温度在低转速下略有降低，在高转速下基本一致，推力在全转速范围内一致。

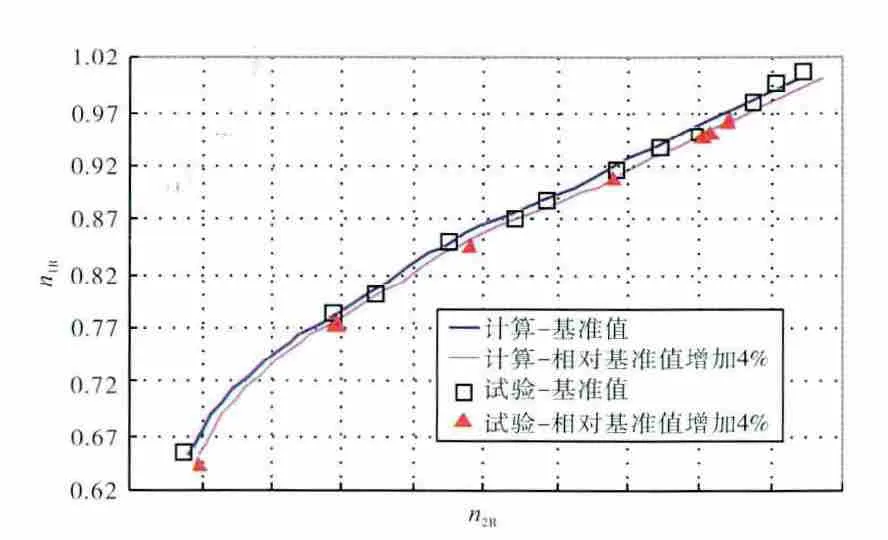
图7 低压涡轮导向器面积变化对转差的影响

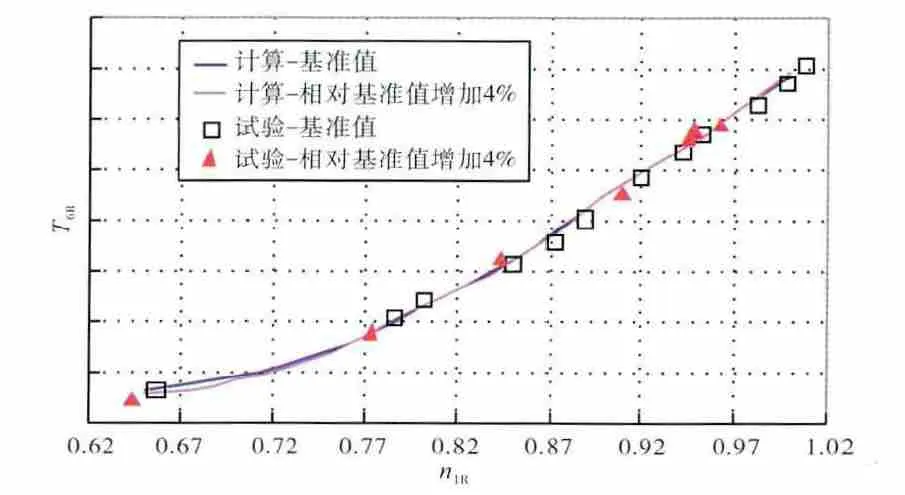
图8 低压涡轮导向器面积变化对排气温度的影响

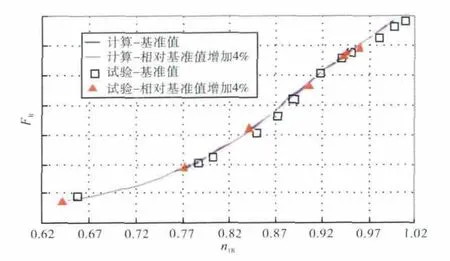
图9 低压涡轮导向器面积变化对推力的影响

4 总结

为满足快速收敛，提高收敛性和收敛效率的要求，设置适合的学习因子、惯性权重、迭代误差限及选择合适的粒子群改进算法，可改善粒子群算法的前段收敛速度和后段的收敛精度。

采用PSO-NR求解本文建立的发动机共同工作方程组，可有效解决高、低压涡轮导向器面积改变对性能影响计算不收敛的问题；采用换特性计算方法的计算结果与试验结果基本一致。改变涡轮导向器面积对发动机性能影响的仿真计算可为发动机调试提供技术支持。

[1]童凯生.航空涡轮发动机性能变比热计算方法[M].北京：航空工业出版社，1991：9-18.TONG Kaisheng.Calculation method of performance with variable specific heat for aviation turbine engine[M].Beijing：Aviation Industry Press，1991：9-18.(in Chinese)

[2]熊纯.航空发动机动态数学模型非线性方程组解法研究[J].长沙航空职业技术学院学报，2002，2（3）：39-42.XIONG Chun.Study on the solution of nonlinear equation group of dynamic mathematical model of aeroengine[J].Changsha Aeronautical Vocational and Technical Collegle Journal,2002，2（3）：39-42.(in Chinese)

[3]李家瑞，孙健国，张绍基.航空发动机总体性能数学模型的1种收敛算法[J].航空发动机，2005，31（4）：48-50.LI Jiarui,SUN Jianguo,ZHANG Shaoji.A convergence algorithm of aeroengine performance mathematical model[J].Aeroengine，2005，31（4）：48-50.(in Chinese)

[4]骆广琦,桑增产,王如根 等.航空燃气涡轮发动机数值仿真[M].北京：国防工业出版社，2007：6-8.LUO Guangqi，SANG Zengchan，WANG Rugen，et al.Numerical methods for aviation gas turbine engine simulation[M].Beijing：National Defense Industry Press，2007：6-8.(in Chinese)

[5]陈长忆，叶永春.基于粒子群算法的非线性方程组求解[J].计算机应用与软件，2006，23（5）：137-139.CHEN Changyi，YE Yongchun.Solving nonlinear systems of equations based on particle swarm optimization[J].Computer Application and Software,2006，23（5）：137-139.(in Chinese)

[6]苏三买，陈永琴.基于混合遗传算法的航空发动机数学模型解法[J].推进技术，2007，28（6）：661-664.SU Sanmai，CHEN Yongqin.Hybrid genetic algoritham in solving aeroengine nonlinear mathematical model[J].Journal of Propulsion Technology，2007，28（6）：661-664.(in Chinese)

[7]刘志雄，梁华.粒子群算法中随机数参数的设置与试验分析[J].控制理论与应用，2010，27（11）：1489-1496.LIU Zhixiong，LIANG Hua.Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm [J].Control Theory&Applications，2010，27（11）：1489-1496.(in Chinese)

[8]张强，李本威，马力.粒子群算法在航空发动机部件模型求解中的应用[J].系统仿真学报，2009，21（12）：3584-3587.ZHANG Qiang,LI Benwei,MA Li.Application of particle swarm optimization in solution to aeroengine component-level model[J].Journal of System Simulation (S1004-731X)，2009，21（12）：3584-3587.(in Chinese)

[9]连志刚，焦斌.一种混合探索的粒子群算法[J].控制理论与应用,2010，27（10）：1404-1410.LIAN Zhigang，JIAO Bin.A particle swarm algorithm based on hybrid exploration[J].Control Theory and Application，2010，27(10)：1404-1410.(in Chinese)

[10]任子晖，王坚.加速收敛的粒子群优化算法[J].控制与决策，2011，26（2）：201-206.REN Zihui,WANG Jian.Accelerate convergence particle swarm optimization[J].Control and Decision Making，2011，26（2）：201-206.(in Chinese)

[11]骆广琦，刘波，宋頔源.基于混合粒子算法的航空发动机数学模型解法[J].燃气涡轮试验与研究，2011，24（2）：5-8.LUO Guangqi，LIU Bo，SONG Diyuan.Hybrid particle swarm optimization in solving aeroengine nonlinear mathematical model[J].Gas Turbine Experiment and Research,2011，24（2）：5-8.(in Chinese)

[12]廉筱纯，吴虎.航空发动机原理[M].西安：西北工业大学出版社，2005：252-255.LIAN Xiaochun，WU Hu.Theory of aeroengine[M].Xi’an：Northwest Polytechnical University Press，2005：252-255.(in Chinese)