开关磁阻电动机的一种磁链建模方法研究*

宋小川，王家军

(杭州电子科技大学 自动化学院，浙江 杭州 310018)

0 引言

随着现代电力电子技术的发展和微处理器的不断更新换代，电动机控制技术也有了显著提高，继传统交、直流调速系统之后出现了新一代的开关磁阻电动机(SRM)调速系统。开关磁阻电动机具有结构简单、成本低廉、容错性高、调速范围宽以及控制灵活等诸多优良特性［1-4］，近年来已被广泛应用于各种驱动与调速系统领域。然而开关磁阻电动机高度的非线性性、特殊的双凸极结构以及通常工作于磁饱和状态等特点使得其运行特性难以被解析方程精确地描述［5-6］，因此，传统电动机的分析、建模方法难以应用到开关磁阻电动机的研究之中，尤其是体现开关磁阻电动机多变量耦合关系的磁链特性的获取相当困难。由于开关磁阻电动机磁链的变化不仅依赖于电流，同时还随着转子位置发生变化，难以得到磁链-电流-位置角之间的解析关系，这是开关磁阻电动机数学建模过程中较为突出的难点问题。

开关磁阻电动机磁链特性的获取有多种方法，较为常用的有:有限元分析法［7］、解析法［8］和实验测量法。虽然有限元分析法的结果精度较高，但需要测量精确的电动机元件的几何尺寸和详细的电动机基本参数，且计算量大，对于给定的电动机并不适用;解析法是先对一些特殊位置的磁链特性及相关参数进行测量，然后通过数学分析方法估算出完整的磁链特性，此方法虽能够反映磁化规律，但并非电动机实际的磁链特性，更适用于仿真研究;实验测量法既能够准确地测量出电动机的实际磁链特性，实现过程也较为简便，也没有繁琐的分析计算，因此，实验测量是一种较为理想的磁链特性获取方法。

基于实验法，本研究对一台四相8/6 极开关磁阻电动机的磁链特性进行测量，得到样机的磁链模型，给出实验方法和步骤，并和分析法所建立的模型进行对比，以验证本研究的建模方法的正确性和有效性。

1 开关磁阻电动机的数学模型

开关磁阻电动机作为一种典型的机电一体化装置，具有基本的电磁特性和机械特性，并可列写描述这些特性的电路方程、机械方程和机电联系方程。其电磁特性可由电压平衡方程描述，即:

式中:Ψ(θ，i)—电动机任意相的磁链;v(t)，i(t)，R—该相绕组的电压，电流和电阻值;θ—该相所对应的转子位置角。

开关磁阻电动机的机械特性可由其机械运动方程描述，即:

式中:ω—转子角速度;T(θ，i)，TL—开关磁阻电动机的电磁转矩和负载转矩;J，B—系统的转动惯量和摩擦系数;即:

与在N、S 磁场中受力而产生转矩的传统电动机不同，开关磁阻电动机的转子是沿着使磁路的磁阻最小的方向，由非对齐位置向对其位置转动。其电磁转矩T(θ，i)为磁共能的非线性函数，随着不同位置处磁共能的变化而变化，即:

式中:W'(θ，i)—电动机的磁共能，由各位置磁链对电流的积分得到，即:

从文化上讲，幼发拉底河和底格里斯河是美索不达米亚文化，后来的希伯来文化、阿拉伯文化的起源地，也是世界四大文明的发祥地之一。犹太人创立了犹太教，灭国以后，犹太人被掳到埃及，说是从摩西带领以色列人出埃及时开始撰写《摩西五经》，其实是犹太人被掳到巴比伦以后才开始写作《摩西五经》。犹太教义被传播，才有了基督教。如果承认西方文明的两“希”(希伯来、希腊)起源的话，更应该尊重“巴比伦”的称谓，不是连伯特曼也承认巴比伦的《汉谟拉比法典》是世界上第一部法典吗？

显然，方程(4，5)的解需要得到磁链Ψ、电流i和位置角θ 三者之间关系，即磁链特性Ψ(θ，i)。因此，开关磁阻电动机数学建模的关键在于获取磁链特性Ψ(θ，i)以求得各系统变量之间的关系。由式(1～5)可以得到开关磁阻电动机各系统变量之间的关系，如图1 所示。

图1 开关磁阻电动机模型结构

2 开关磁阻电动机磁链特性的测量

2.1 实验基本原理及电路

电动机的磁链特性若采用直接测量的方法需要昂贵的磁链传感器和复杂的安装调校过程，因此通常采用间接法。对式(1)变形可知，开关磁阻电动机的磁链可由绕组的电感压降对时间的积分得到，即:

由此可见，磁链特性可通过先测量电动机绕组电压v(t)和电流i(t)再进行积分计算间接获取。间接测量法又可分为交流法、交/直流法和直流法。交流法使用交流电源供电，在测量过程中需要给电动机绕组安装探测线圈，且测得磁链和电流均小于实际值，实验的可行性和结果并不理想。交/直流法将先使用整流滤波电路将交流电转化为直流电再进行实验，但交流电源的谐波分量仍然会影响实验结果，并造成不可忽略的误差。直流法使用直流电源直接供电，即无需加设探测线圈也可避免交流电源的谐波问题，与此同时，绕组中通入直流脉冲电压比交流正弦电压更接近于开关磁阻电动机的实际供电模式。因此，本研究采用一种简单便捷的直流方法。

假定开关磁阻电动机的各相绕组完全相同且相互独立，则只需对其中的任意一相进行测量。由于磁链Ψ(θ，i)是相电流i和转子位置角θ 的二元函数，需要对一个周期内各位置的磁化特性Ψ－i 分别进行测量。电动机转子将会被固定在某一特殊位置，通常从对齐位置或非对齐位置开始，并向电动机绕组供以直流脉冲电压，记录下整个过程绕组的电压v(t)和电流i(t)的变化，将数据导入计算机，再结合已知的绕组阻值R，由式(6)进行积分计算便可得到该位置的磁化特性Ψ－i。此时笔者将电动机转子向下一个位置转动一个角度再次进行上述实验过程，以此类推直到测完一个周期的磁化特性Ψ(θ，i)。

实验电路原理图及实物图如图2 所示。L和R2为待测电动机任意一相绕组的等效电路，分别代表相电感和相电阻。绕组经过功率开关元件IGBT 连接电源VCC。为了避免交流电源的谐波和电路中的RLC 振荡所引起的误差，本研究采用一种精密可调直流稳压电源供电，结合稳压电容C1，具有比需进行整流滤波的交流电源更好的稳压能力。本研究使用数字示波器测量并记录绕组电压v(t)，以及测试电阻R1的电压以间接计算电流i(t)，并将实验数据输入计算机进行数值计算。续流二极管的作用是在IGBT 关断时为所测绕组提供释放能量的通道。IGBT 的通断由信号发生器来控制。

图2 实验电路原理图及实物图

2.2 实验的基本步骤

本研究的实验对象为一台四相8/6 极开关磁阻电动机，被测样机基本参数如表1 所示。该实验将对电动机从对齐位置(30°)到非对齐位置(0°)之间各位置的磁化特性进行测量。测量时，电动机转子被分度卡盘固定在特定位置，并供给18 V 的直流脉冲电压。由于相绕组阻值很小(1.8 Ω)，且转子堵转无感应电动势，为了避免瞬间电流过高而烧坏绕组，功率开关元件的工作周期不宜过长，且导通时间应比关断时间小得多。与此同时，还应保证电流能够达到饱和，经过调试，将信号发生器输出的IGBT 触发信号频率设置为1 Hz，占空比设置为10%可满足实验要求。为了准确地找到实验初始对齐位置(30°)，本研究可对绕组供电并让转子自由转动，转子会最终停止在对齐位置。当测完对齐位置的数据，笔者将转子转动3°进行下一个位置的测量，以此重复，直到测完非对齐位置(0°)为止。至此，笔者将数据输入计算机进行积分运算便可得到半个周期的磁链特性。由于开关磁阻电动机对齐位置两侧的磁链特性是对称的，只需对半个周期的磁链特性进行测量。

表1 被测样机基本参数

3 实验结果与分析

本研究以3°为步距角进行了测量实验，得到0°，3°，6°，…，30°，共11个位置的实验数据。部分位置的绕组电压、电流波形如图3 所示。图象上方为绕组电压波形(10 V/格)，下方为描述绕组电流的测量电阻的电压波形(1 V/格)，示波器采样周期为1 ms。从图3 中可以看出，由于电动机绕组为感性负载，电流需要一定的时间达到稳态值，IGBT 关断后电压立即减为零，电流通过续流二极管释放。越接近对齐位置(30°)电流上升速度越慢，这是因为越接近对齐位置电路的电感越大，故时间常数越大。

式中:k—采样点的序列;k=1，2，3，…，Ts—采样周期，该实验中为1 ms。

图3 不同位置的绕组电压电流波形

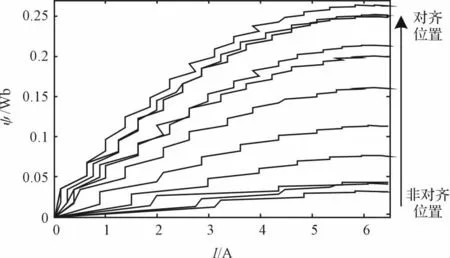
图4 未经滤波的磁链特性

由于开关磁阻电动机转子无永磁体，因此磁链的初始值Ψ(0)=0。未经滤波的磁链特性如图4 所示。若将原始数据直接进行积分运算，计算相对繁琐，所得到的磁链特性曲线会因为测量误差以及噪声等因素的干扰而存在较大的波动。因此，为了简化计算以及对原始实验数据进行滤波，本研究将使用Simpson 1/3 法则进行积分运算［9-10］，可将式(7)转化为:

式中:k=2，4，6，…;Ψ(0)=0;Ts=0.001 s。

将计算结果进行3 阶多项式拟合［11-12］，可得滤波处理后半个周期内不同位置下磁链特性曲线如图5所示。

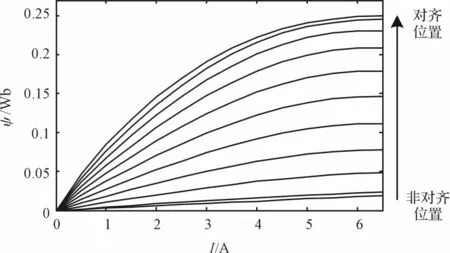
图5 滤波处理后的磁链特性

从图5 中可以看出在对齐位置和非对齐位置附近磁链特性曲线分布较为密集，中间位置分布较为平均。越接近对齐位置曲线弯曲程度越大，越接近非对齐位置曲线越接近直线。由此可见，开关磁阻电动机具有很强的非线性性，并且在越接近对齐位置处越显著。这是由于转子越靠近定子时电感值越大，当定转子完全对齐后电感达到最大值。由开关磁阻电动机电感与磁链的关系，可得到:

即得到电动机在不同电流值下的电感曲线，如图6 所示。可见在同一位置下，电感值越大电流越小，且越接近对齐位置电感对电流的影响越大。

图6 不同电流对应的电感曲线

最后，本研究将用文献［13］中提出的解析法建立磁链模型，与本研究建立的模型进行对比。文献［13］提出的方法首先需要确定非对齐位置和对齐位置的磁化特性的解析式Ψq和Ψd，再基于这两个特殊位置的磁化特性用非线性方程计算其余各位置的磁化特性。非对齐位置磁链与电流呈线性关系，即:

式中:Lq—非对齐位置电感。

对齐位置磁化特性由非线性方程描述，即:

式中:Ldsat—对齐位置饱和电感;A，B—常数，可由下式确定，即:

式中:Ld—对齐位置不饱和电感;Im、Ψm—最大电流及最大电流对应的最大磁链。

对齐位置和非对齐位置之间各角度处磁链与电流关系可由非线性函数Ψ(θ，i)确定，即:

式中:Nr为转子极数。

因此，本研究得到电动机Lq、Ld、Ldsat、Im、Ψm5个参数，便可由上式(14、15)得到磁链与电流和位置角之间的关系。基于该实验所测量数据，本研究可确定样机对应参数分别为Lq=0.003 H、Ld=0.092 H、Ldsat=1.79 mH、Im=6.5 A、Ψm=0.25 Wb，由此可计算得到电动机不同位置的磁链特性曲线如图7 所示。经过对比可以看出两种方法所建磁链模型较为吻合，磁化规律基本一致，解析法所得结果略低于实验法所得实际值，进一步验证了本研究使用方法的正确性和有效性。

图7 解析法所得磁链模型

4 结束语

本研究提出了一种基于实验测量的开关磁阻电动机磁链建模方法，详细介绍了实验原理和步骤以及实验数据处理方法，并对一台四相8/6 极开关磁阻电动机进行了实验，获取了样机的磁链模型，同时与采用解析的方法建立的样机的磁链模型进行了对比。

实验结果表明，本研究提出的方法易于实现、成本低，所建模型具有较高的精度，准确地获取磁链特性对于下一步开关磁阻电动机的分析、仿真以及控制策略的研究具有重要意义。

［1］MILLER T J E.Switched reluctance motors and their control［M］.Oxford:Magna Physics Publishing and Clarendon Press，1993.

［2］KRISHNAN R.Switched reluctance motor drives［M］.Florida:CRC Press，2001.

［3］MILLER T J E.Electronic control of switched reluctance machines［M］.Oxford:Newnes Press，2001.

［4］詹琼华.开关磁阻电动机［M］.武汉:华中理工大学出版社，1992.

［5］俞枭辰，王家军.开关磁阻电动机实验平台的开发与研究［J］.机电工程，2014，31(5):600-606.

［6］王洪诚，陈 刚，王钰涵，等.基于线性模型的开关磁阻电机控制系统［J］.兵工自动化，2012，31(6):70-73.

［7］PARREIRA B，RAFAEL S，PIRES A J，et al.Obtaining the magnetic characteristics of an 8/6 switched reluctance machine:from FEM analysis to the experimental tests［J］.IEEE Transactions on Industrial Electronics，2005，52(6):1635-1643.

［8］SHEN Lei，WU Jian-hua，YANG Shi-you，et al.Fast flux linkage measurement for switched reluctance motors excluding rotor clamping devices and position sensors［J］.IEEE Transactions on Instrumentation and Measurement，2013，62(1):185-191.

［9］TSENG C-C.Digital integrator design using simpson rule and fractional delay filter［J］.IEE Proceedings:Vision，Image and Signal Processing，2006，153(1):79-85.

［10］尚 涛，谢龙汉，杜如虚.Matlab 工程计算及分析［M］.北京:清华大学出版社，2011.

［11］NAKAMURA S.科学计算引论:基于Matlab 的数值分析［M］.梁恒译.北京:电子工业出版社，2002.

［12］MATHEWS J H，FINK K D.数值方法:Matlab 版［M］.周璐译.北京:电子工业出版社，2010.

［13］LE-HUY H，BRUNELLE P.A Versatile Nonlinear Switched Reluctance Motor Model in Simulink Using Realistic and Analytical Magnetization Characteristics［C］// Proceedings of the 31st Annual Conference of the IEEE Industrial Electronics Society.Raleigh:［s.n.］，2005:1556-1561.