基于顾客服务水平的物流网络优化问题

单而芳，孙广帅（上海大学 管理学院，上海 200444）

0 引言

物流网络设计问题是供应链设计中的一个主要问题。以往研究物流网络设计问题的文献主要将物流网络设计问题分为三个层面，即战略层面、策略层面和运营层面。从战略和策略层面上来研究，Miller[1]利用一个混合整数规划模型解决了铁路网络选址的最优化问题；Crainic[2]利用数学规划的方法做了一个内部服务网络的优化设计；Melkote和Daskin[3]使用混合整数规划将设施选址的问题和网络设计问题结合在一起；Drezner和Wesolowsky[4]运用启发式算法介绍了一种确定设施连接的网络设计问题；高阳和李雪[5]针对逆向物流网络的多目标和回收废旧品数量的不确定性，建立了随机多目标规划模型；廖伟和潘瑶[6]考虑碳的成本和环境双重因素，建立起碳交易下的低碳销售物流网络优化模型；伍星华和王旭[7]以再制造闭环物流网络设计为研究对象，以总运营收益最大为目标，建立了再制造闭环物流网络的同周期优化设计模型。然而，随着对于物流网络的逐渐深入的研究，学者们考虑更多的是将战略、策略层面与运营层面相结合，从单一的物流网络路线设计问题转为对物流网络设计和商品运输、加工处理、仓储以及销售相结合的问题上来。例如：Jayaraman[8]在FLP结构中加入了EOQ库存模型和采购成本（假设库存有确定的批量和确定的需求）；Nozick和Turnquisk[9]提出了一个关于完全库存成本的线性函数，并将其作为设置分配中心的函数；Daskin，Coullard和Shen[10]，Miranda和Garrido[11]发表了相似的FLP模型关于库存控制决策的文献；Miranda和Rarrido[12]提出了通过控制安全库存来解决物流网络设计的问题。最近Jiuh-Biing Sheu和Alex Y.-S.Lin[13]提出了利用分层的网络设施区解决全局物流网络设计的问题；周向红和高阳[14]考虑废品回收中心的处理能力限制和库存成本，以回收网络系统利润最大化和社会效益最大化为目标，建立了多周期多目标的废旧品回收网络模型；韩雪和张邻[15]通过考虑服务水平、物流成本以及产品价格之间的相互作用，建立了物流网络双层规划模型。

通过上述的文献可以看出，目前的物流网络设计的研究更多的在于将策略和战略层面同运营层面相结合，理论联系实际，在传统的选址问题的基础上，加大了对于商品运输、加工处理、存储以及销售等细节方面的研究。

本文主要是对供应链中商品在基于顾客服务水平下的物流网络设计的优化研究。通过将物流网络中策略和运营层面的问题相结合，将传统的选址问题、定价问题以及顾客的服务水平等问题结合起来去考虑，将原本静态的数学模型转变为动态模型。使其与现实问题更加契合。最后，通过将选址、定价以及顾客服务水平的结合，又找出了顾客服务水平与零售价格之间的关系，具有一定的现实意义。

1 背景介绍

如图1，供应商i经由配送中心j运输的商品数量为Yij，由配送中心j到零售商k运输的商品数量为Xjk，而零售商接收到订购的货物后，又需要将货物提供给顾客以满足顾客的需求。

在此研究背景下，对于供应商会有几个策略上的计划问题：

（1）决定挑选哪几个配送中心来加工和处理商品。

（2）确定由供应商经由配送中心j货物Yij的数量。

（3）确定经由配送中心j到达零售商k的货物Xjk的数量。

（4）确定商品的批发价格。

对于零售商会有运营上的计划问题：确定仓库库存的服务水平等级。

另外，在本问题中还要做出以下的几个假设：

（1）顾客的需求是不确定性的；

（2）零售商k与仓库之间的距离可以忽略为0；

（3）由于本文中研究的零售商与顾客是1对1的，所以根据Miranda[12]的研究中提出的假设：顾客的需求概率密度函数与仓库的库存概率密度函数相等。即用1-α表示顾客需求的概率（同时也表示仓库库存的概率），Z1-α表示仓库库存的安全系数。由于顾客的服务水平与顾客的需求概率呈正相关关系。顾客的需求概率等于仓库库存的概率，而根据库存安全系数的定义来看，仓库库存概率与仓库安全系数呈正相关。故可以推出：顾客的服务水平与仓库的安全系数是正相关关系。

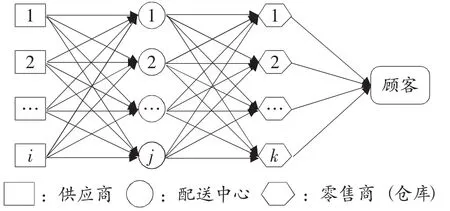
图1 运输配送网络

2 数学模型

2.1 参数和变量

Q*i：每个供应商i最大提供的商品量；

Qk：零售商k订购货物的量；

Dk：顾客k每日的平均需求量；

pk：供应商卖给零售商k的商品的批发价格；

Yij：供应商i经过配送中心j运输商品的数量；

Xjk：经由配送中心j到零售商k运输商品的数量；

ej：建设配送中心j所需要的固定成本；

bj：为0-1变量，0：j被选为配送中心，1：j不被选为配送中心；

αij：从供应商i经由配送中心j的单位的运输成本；

βjk：由配送中心j到零售商k的单位运输成本；

cj：配送中心j加工处理货物的单位成本；

dk：顾客k每日需求的不确定量；

Fk（q）：顾客k的需求量q的概率密度函数；

φk：零售商k的零售价；

hk：零售商k仓库商品的单位储存成本；sk：零售商k仓库商品的单位缺货成本；

LTk：零售商k的补货提前期；

（1-α ）k：零售商k对应顾客需求的概率；

Z（1-α）k：零售商k仓库的库存安全系数。

2.2 目标函数

由于供应商要确定在物流网络中得到最大的收益，他们需要考虑以下的几个因素：

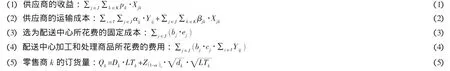
综上，供应商的目标函数可以写为：

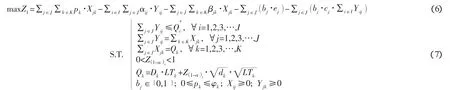
另一方面，零售商k的利润需要考虑以下几个因素：

（1）零售商k订购商品的成本：

（2）零售商k的销售收益：

（3）零售商k剩余商品的持有成本：

这里 ［Qk－ Dk］+=max｛ Qk－ Dk,0｝

（4）零售商k的缺货成本：

这里 ［Dk－ Qk］+=max｛ Dk－ Qk,0｝

通过上面这些因素，可以将零售商的利润目标函数写成：

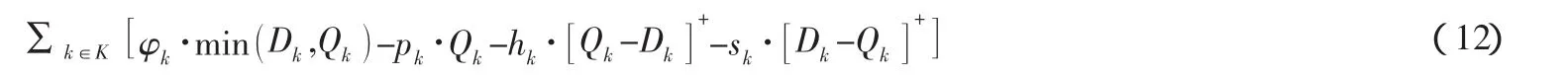
由于顾客的需求是不确定性的，所以我们只能确定零售商的期望利润。基于公式（12），零售商的利润目标函数可以表示为：

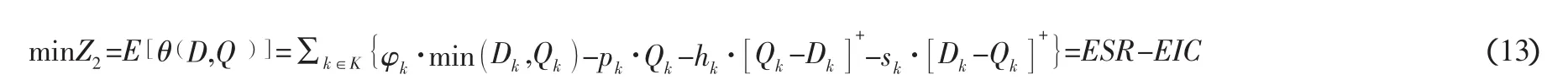
用ESR表示所有零售商销售利润，它可以表示为：

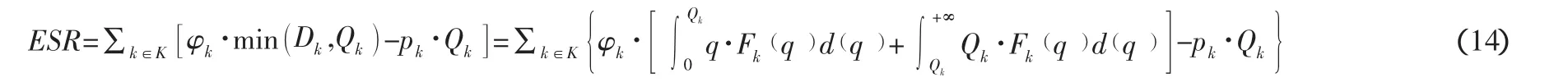
用EIC表示在顾客需求不确定性条件下的期望仓库成本，它可以表示为：

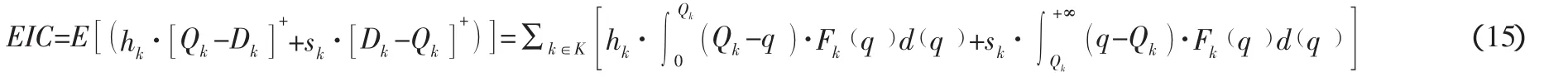
整理之后可以得到：

3 理论方法

对于供应商的数学模型来讲，它是一个非线性的混合整数规划的问题，本文是利用软件Lingo来对这一问题进行求解。

对于零售商的数学模型，首先Adelman[16]和Javid[17]证明它的目标函数是凹的（保证它的二阶导数是大于0的）。因此，如果我们认为E［ θ（ D,Q ）］是一个关于Qk的连续函数，那利润最大的点是可以通过来获得。

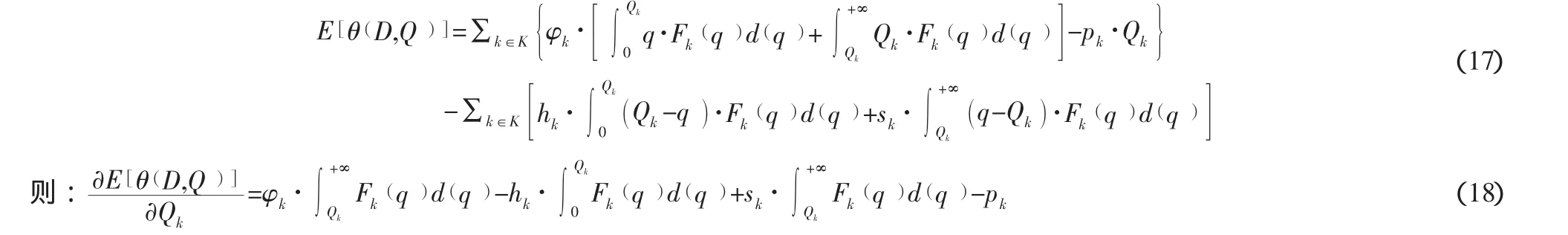
则可以得到：

另外，根据Pablo A.Miranda[10]在文献中得到的结果顾客需求的概率所以我们可以推导出1-α

基于上述的分析，我们分别得到供应商利润最大和零售商利润最大的数学模型。但是，要同时求得两者利润最大的结果，本文使用到遗传算法。算法的步骤如图2所示：

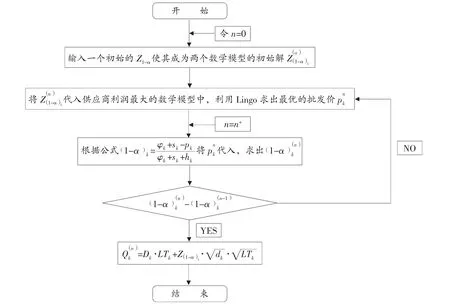
图2

4 实证分析

由于文章中数学模型中的变量和参数比较多，在现实中难以获得全部的真实数据，所以文章用随机数来对模型进行模拟，并验证是否能求得最优解。

4.1 首先根据顾客需求概率1-α的未知和已知，我们可以将数学模型分为两种情况：

4.1.1 当顾客需求概率1-α为已知时，那可以直接根据公式，来求得订货量Qk和供应商的批发价pk。

模型中各参数取值如表1、表2：

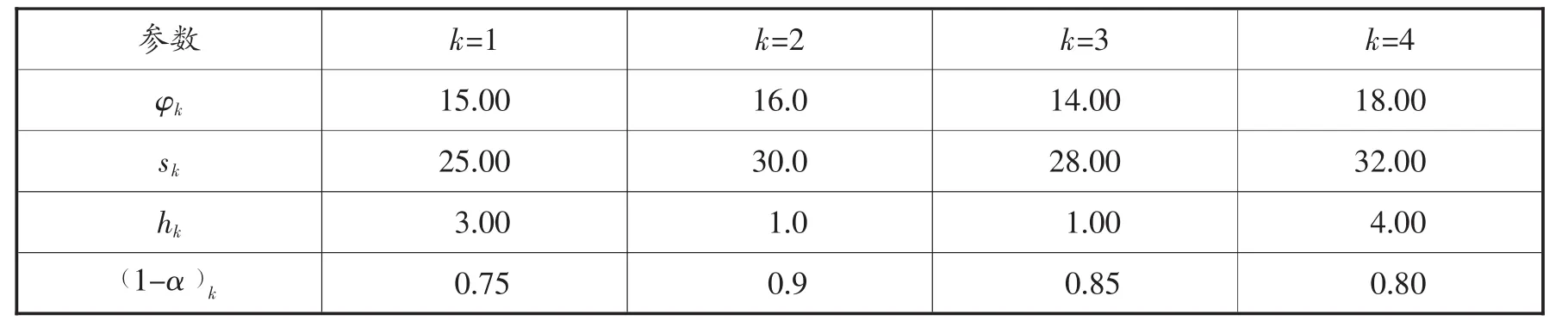
表1

表2

经过计算可以得出：

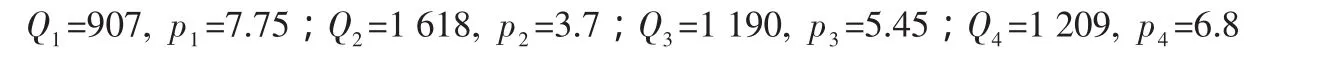
4.1.2 当顾客需求概率1-α未知时，则需要根据图2的算法进行迭代和计算从而得出最后的最优解如表3～表7：

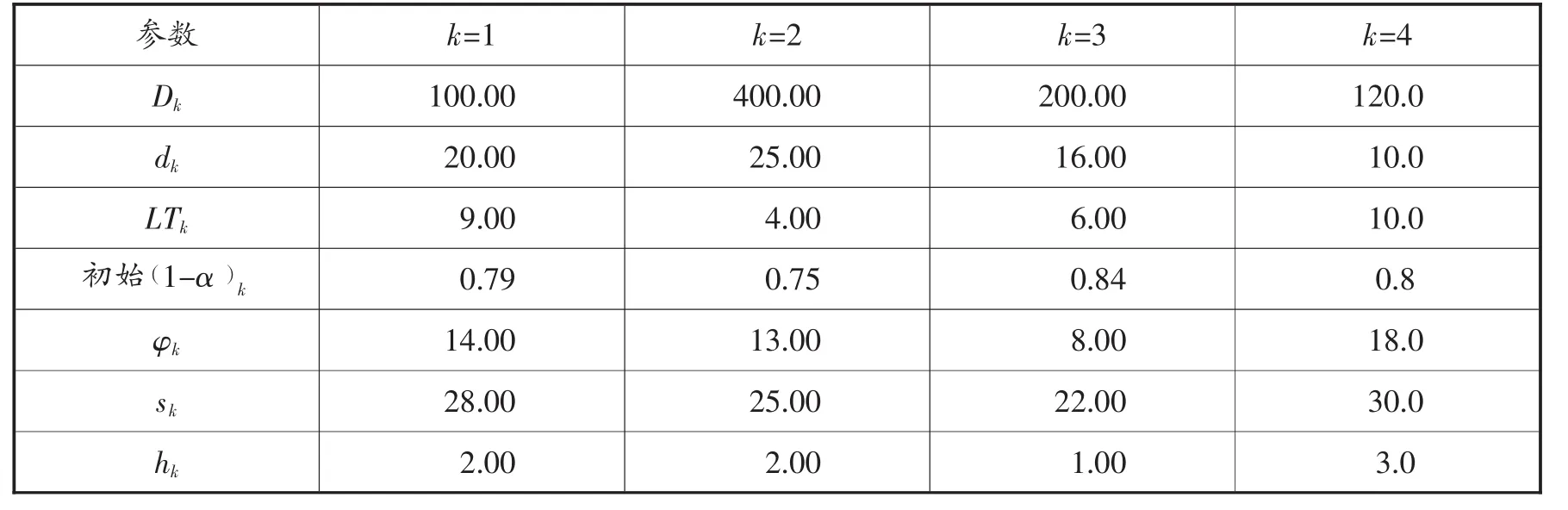
表3

表4

表5

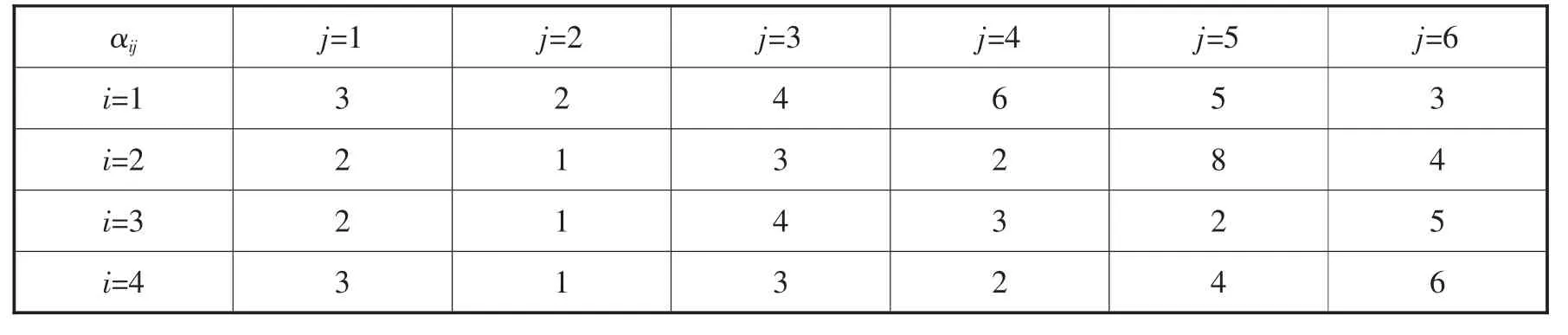
表6

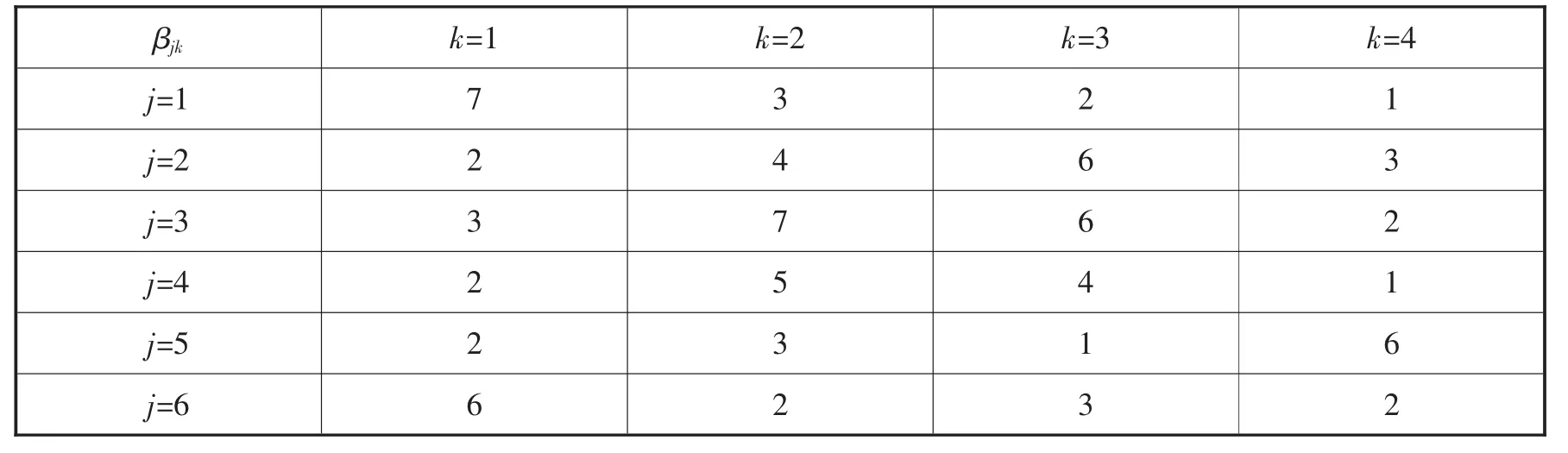
表7

求解得：Q1=909,p1=9；Q2=1 606,p2=9；Q3=1 207,p3=7；Q4=1 208,p4=10。

以上求解得到的都是局部最优解，由于此问题是NP-难问题[18]，所以无法得到全局最优解。

4.2 本文除了求得最优解之外，还将对1-α和φk之间的关系进行分析

首先，在讨论1-α和φk的关系时，前提是以供应商的利益作为主体。所以根据公式，由于供应商的利益为主体，使其利益最大化。即令pk无限接近于φk，可以得到：

由于sk和hk为固定值，所以我们可以看出顾客需求的概率1-α和零售商的零售价φk是呈反函数的关系。同时顾客需求概率1-α和顾客服务水平是呈正相关关系。所以：当sk和hk一定，零售价φk越大，则顾客需求概率1-α越小，相应的顾客服务水平（安全库存系数）也越小；反之零售价φk越小，则顾客需求概率1-α越大，相应的顾客服务水平（安全库存系数）也越大。（如图3所示）

5 结论

本文主要研究基于顾客服务水平下的物流网络的优化设计问题。通过考虑物流运营管理中库存管理以及顾客服务水平的因素，优化了以供应商到配送中心再到零售商的物流网络。解决了供应商与零售商收益最大化的物流设计方案。另外，在考虑供应商为主体，即实现供应商利益最大化的前提下，得到顾客需求概率与零售价之间的函数关系，并且又推导出顾客服务水平与零售价呈负相关关系这一结论。对于现实中满足顾客需求同时保证零售商利益最优情况，有着一定的借鉴作用。现实中，由于涉及服务水平的因素是多方面的，因此考虑更多与服务水平相关的因素并且寻找它们与服务水平之间的变化关系是需要进一步探索的重要问题。

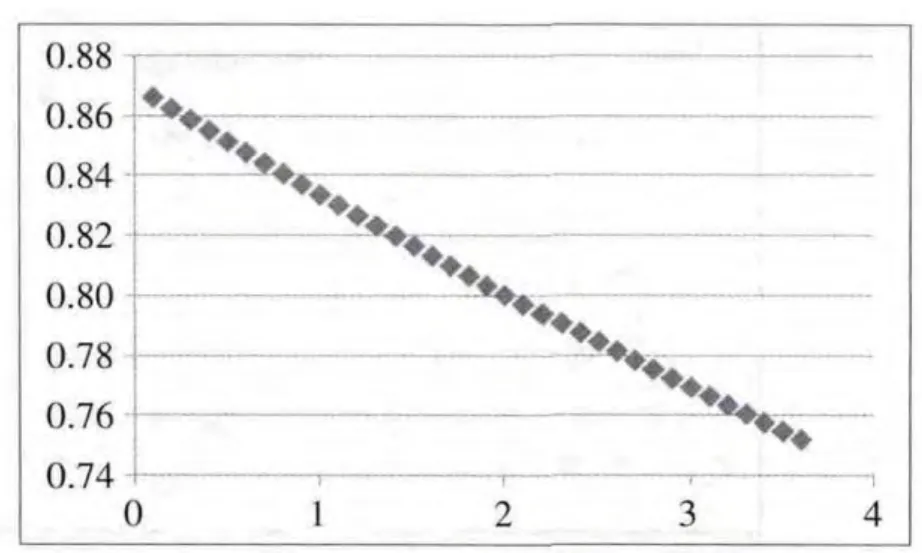
图3 sk为20，hk为3的顾客需求的概率1-α和零售商的零售价φk的关系图

[1] T.Miller,D.Wise,L.Clair.Transport network design and mode choice modeling for automobile distribution:a case study[J].Location Science,1996(4):37-48.

[2] T.G.Crainic.Service network design in freight transportation[J].European Journal of Operational Research,2000,122:272-288.

[3] S.Melkote,M.S.Daskin.Capacitated facility location/network design problems[J].European Journal of Operational Research,2001,129:481-495.

[4] Z.Drezner,G.O.Wesolowsky.Network design:selection and design of links and facility location[J].Transportation Research Part A,2003,37:241-256.

[5] 高阳，李雪.随机环境下再制造逆向物流网络选址研究[J].数学的实践与认识，2013(16):27-34.

[6] 廖伟，潘瑶，贺政纲.考虑碳交易的销售物流网络优化[J].统计与决策，2013(12):176-179.

[7] 伍星华，王旭，代应.再制造闭环物流网络的多周期优化设计模型[J].计算机集成制造系统，2011(9):2015-2021.

[8] V.Jayaraman.Transportation,facility location and inventory issues in distribution network design[J].International Journal of Physical Distribution&Logistics Management,1998,18(5):471-494.

[9] L.K.Nozick,M.Turnquist.Integrating inventory impacts into a fixed-charge model for locating distribution centers[J].Transportation Research Part E,1998,34(3):173-186.

[10] M.S.Daskin,C.Coullard,Z.-J.M.Shen.An inventory-location model:Formulation,solution algorithm and computational results[J].Annals of Operations Research,2002,110(1):83-106.

[11] P.A.Miranda,R.A.Garrido.Incorporating inventory control decisions into a strategic distribution network design model with stochastic demand[J].Transportation Research Part E,2004,40(3):183-207.

[12] P.A.Miranda,R.A.Garrido.Inventory service-level optimization within distribution network design problem[J].International Journal of Production Economics,2009,122:276-285.

[13] J.B.Sheu,A.Y.S.Lin.Hierarchical facility network planning modelfor global logistics network configurations[J].Applied Mathematical Modelling,2012,36:3053-3066.

[14] 周向红，高阳.基于动态定价的多周期多目标产品回收网络设计[J].系统工程，2013(91):93-97.

[15] 韩雪，张邻.客户价值导向的竞争性物流网络双层规划模型[J].公路交通科技，2013,2(30):140-146.

[16] D.Adelman.A price-directed approach to stochastic inventory/routing[J].Operations Research,2004,52:499-514.

[17] A.A.Javid,N.Azad.Incorporating location,routing and inventory decisions in supply chain network design[J].Transportation Research Part E,2010,46:582-597.

[18] P.A.Miranda,R.A.Garrido.e-Work based collaborative optimization approach for strategic loaistic network design problem[J].Computer&Industrial Engineering,2009,57:3-13.