基于鲍摩-瓦尔夫模型及算法在木材仓储中心选址中的应用

豆佳梅，孟利清，钱良辉，潘 祥（西南林业大学 机械与交通学院，云南 昆明 650224）

在木材仓储中心的选址规划过程中，如何确保总的木材仓储成本和运输成本最优化，是非常重要的问题。由于木材生产的地域性、季节性与需求的分散性、广泛性之间的矛盾，使得木材物流相当复杂，随着木材物流运输仓储等问题的不断出现，不少林产企业已经充分认识到木材物流的重要性，迫切希望通过木材仓储选址的优化提高木材物流管理水平以及降低木材的运输成本，以开发木材行业的第三利润源，目前我国对于木材物流研究仍不很深入，相关研究报道较少，而鲍摩－瓦尔夫模型及算法的应用发展为之提供了切实可行的实现途径，在这种背景下，研究木材仓储中心选址优化并加以应用是十分及时和必要的。

对于拟定的木材仓储中心选址，要能确保一定区域内木材运输、仓储过程中的最佳方案，以达到总运输费用和仓储费用最小化的目的。

1 问题描述及模型建立

有m个伐区楞场，经过木材仓储中心发售给n个地区的需材点。其中楞场伐区的生产能力已知，每个需材点的需求量已知。模拟建立若干个木材仓储中心，候选地点有S个，问题是如何从S个候选地点中选择若干个地点作为木材仓储中心，使木材物流费用达到最小。上述问题可以简单表述为：在伐区楞场、需材点一定的情况下，在若干个备选地址中，找出木材物流节点的数量和位置，使得通过木材物流节点所运送的木材的固定成本和可变成本在下列约束条件下最低：（1）不能超过每个伐区楞场的供货能力；（2）所有需材点的需求必须得到满足；（3）每个木材仓储中心的总进货量等于总出货量。

式中：i为楞场伐区（i=1,2,…,m ）；j为木材仓储中心（j=1,2,…,s）；k为需材点（k=1,2,…,n ）；Ai为楞场伐区i的供应量（i=1,2,…,m ）；Bk为需材点k的需求量（k=1,2,…,n ）；Cij为从楞场伐区i到木材仓储中心j的单位运输成本；Djk为从木材仓储中心j到需材点k的单位运输成本；Zj为木材仓储中心j的产品通过量；Vj为木材仓储中心j的固定费用；r（ Zj）为Zj=0时取0，否则取1；Wj为木材仓储中心j每单位通过量的变动成本（在考虑变动成本时，引进指数p，满足条件0＜p＜1，以便考虑木材仓储中心的规模经济性，木材仓储中心j的变动费用为WjZjp，如果不考虑规模的经济性，可令p=1）；Xij为伐区楞场i到木材仓储中心j的运量；Yjk为木材仓储中心j到需材点k的运量。

2 模型求解

由于木材物流总成本函数是非线性的，因此，上述问题是一个非线性规划问题，可以先求出初始解，然后迭代计算，主次逼近最优解。步骤如下：

第一步，求初始解，首先对伐区楞场与需材点之间的所有组合（i,k），求每单位运输成本最小值。即求出从伐区楞场i到需材点k的运输成本最低的路线，其运输成本为：C0ik=min｛ Cij+ Djk｝

注意式中左边下标（i,k ）对应于某一个j值，引入变量Uik，表示从伐区楞场i经过某一个木材仓储中心j到需材点k的流通量。解如下线性规划（运输）问题：

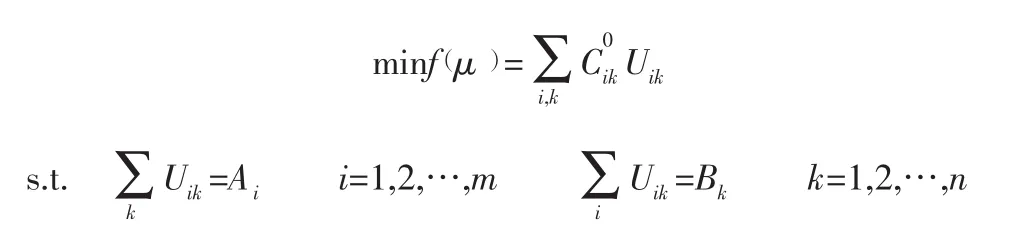
所有 Uik＞0

求出Zj的初次解Z0i。

第二步，求二次解，设经过木材仓储中心j的所有（i,k）组成的集合为G（j），那么：

以运输成本和变动费的合计最小为目标，求得最优路线，即令：上式是由配送总成本函数微分所得的每单位的总成本。解如下线性规划问题：

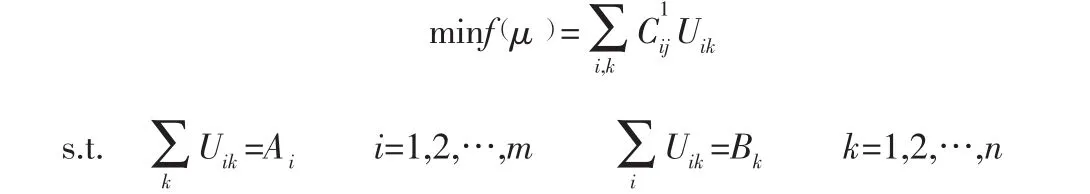
所有 Uik＞0

利用所求的解Uik，求出对应的Z1j。

第三步，求最优解，按第二步方法反复计算，将（n－1）次解的木材仓储中心通过量与n次解的木材仓储中心通过量Znj进行比较，如果相等则终止计算，所得的解就是最优解。

3 算法分析

本例中有两个伐区楞场A1,A2，故i=2；两个伐区楞场向8个地区供应木材，在每个地区各有一个需材点，故k=8。现有5个木材仓储中心候选地D1,D2,D3,D4和D5，选择哪几个木材仓储中心使得总的运输成本最小，故j=5。在此，要考虑规模经济量，即运输费用与木材通过量呈非线性关系。已知条件如伐区楞场到木材仓储中心候选地的单位运输成本（Cij）见表1，木材仓储中心候选地的变动费（WjZpj）见表2，木材仓储中心候选地的变动成本（Djk）见表3。

表1 伐区楞场到木材仓储中心候选地的单位运输成本（Cij）

表2 木材仓储中心候选地的变动费（W jZ p j ）

3.1 初始解。对于伐区楞场到需材点的所有组合，找出使运输成本和配送成本之和为最小的木材仓储中心，见表4。解运输问题得到初始解，见表5。

表3 木材仓储中心候选地的变动成本（Djk）

表4 最小运输成本

表4 最小运输成本

注：括号内的Dj表示通过的仓储中心

需材点伐区楞场A1 B1 B2 B3 B4 B5 B6 B7 B8（D1）17（D1）10（D2）15（D2）20（D2）27（D2）43（D2）37（D2）47 A2（D1）37（D2）26（D3）17（D3）12（D3）16（D4）20（D4）24（D5）22

表5 初始解

3.2 第二次解。利用初始解，可以求出各木材仓储中心候选地的通过量Z0j，进而求出C1ik。由于取p=0.5，所以木材仓储中心单位量费用（变动费）按公式计算。各数据结果见表6和表7。

表6 木材仓储中心通过量和变动费用

表7 最小运输成本

表7 最小运输成本

需材点伐区楞场A1 B1 B2 B3 B4 B5 B6 B7 B8（D1）32（D1）25（D1）33（D3）40.5（D3）44.5（D4）55（D3）54.5（D4）59 A2（D1）52（D3）44.5（D3）32.5（D3）27.5（D3）31.5（D4）30（D4）34（D4）34

再对伐区楞场到需材点的所有组合，选择运输成本、配送成本与变动成本之和的最小值，对应的流动路线为最省路线，然后求解运输问题，得到第二次解，见表8。

表8 第二次解

3.3 第三次解。利用第二次解，求出各木材仓储中心候选地的通过量Z1j，进而求出C2ik。由于D2和D5没有通过量，为了以后讨论中除掉这两个木材仓储中心候选地，设D2和D5的变动费为无穷大，见表9。以此为基础，对伐区楞场到需材点的所有组合，求出总成本最小值，然后求解运输问题，得到第三次解，见表10和表11。

表9 木材仓储中心第二次通过量和变动费用

表10 最小运输成本

表10 最小运输成本

需材点伐区楞场B1 B2 B3 B4 B5 B6 B7 B8 A1 A2（D1）27.6（D1）47.6（D1）20.6（D1）40.6（D1）28.6（D3）32.5（D1）37.6（D3）27.5（D1）45.6（D3）31.5（D4）53.5（D4）28.5（D3）54.5（D4）32.5（D4）57.5（D4）32.5

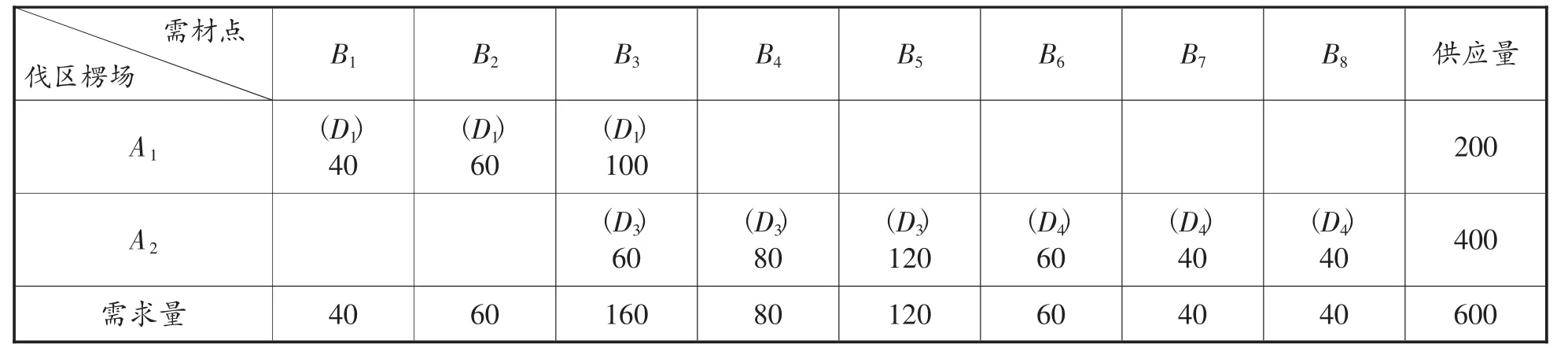
表11 第三次解（最终解）

由于第三次解的通过量与第二次解的通过量相同，所以第三次解便是最终解。由最终解可以看出，在五个候选地中，选取D1,D3,D4三处设置木材仓储中心为宜。

4 结论

木材仓储中心的选址布局对木材物流系统的合理化和经济效益有重要影响。许多数量化、模型化的方法被加以应用并在实际中得到改进。计算较容易，可用物流总成本评价，目标是以最优解木材仓储中心的通过量，决定设施规模，可根据木材仓储中心的变动费，考虑规模的经济性。本文在将鲍摩-瓦尔夫模型用于解决运输费用和木材仓储中心经济规模费用仓储中心选址问题时，表面看来只考虑了经济效益，但是在经济效益中运输成本是由众多因素决定的，木材仓储中心规模的影响在模型中也得到了体现，所以此方法比较综合和客观地反映了木材仓储中心的合理位置。实例分析表明，该方法能方便直观地解决选址问题，是求解此类问题的有效方法。

[1] 李云清.物流系统规划[M].上海：同济大学出版社，2004.

[2] 冯耕中.物流配送中心规划与设计[M].西安：西安交通大学出版社，2004.

[3] 莫海熙，郜振华，陈森发.基于AHP和目标规划的物流配送中心选址模型[J].公路交通科技，2007(5):150-153.