5052铝合金板材的应变硬化行为模型探讨
2014-11-13蔡辉
蔡 辉
(西南铝业(集团)有限责任公司,重庆 九龙坡 401326)
0 前 言
5052铝合金为Al-Mg系热处理不可强化型防锈铝合金,具有良好的成形性、可焊性及中等强度等特性,已广泛地应用于国防军工和民用领域[1~3]。铝合金在加工过程中不可避免的产生加工硬化,了解合金的加工硬化特性,对于确定合金变形工艺有着重要的意义[4、8]。
目前, 5052铝合金不同加工状态下的加工硬化行为的数学模型尚未统一。众所周知,幂函数关系模型即Hollomon方程是描述金属及其合金材料应变硬化应用最为广泛的数学模型[5、6],其数学表达式为:σ=BεN。其中,B、N为材料常数,此时应变硬化指数n=N=dlnσ/dlnε。由于Hollomon方程中n值为常数,其对应的lnσ~lnε曲线为直线,而实际情况中不同组织、不同变形条件下的lnσ~lnε曲线并非恰好如此。因此,为了提高应变硬化数学模型的精度,通过Hollomon方程衍生出式(1)、式(2)和式(3)等经验关系模型,数学表达式如下:

其中,B、ε0、N、C均为常数,式(3)为上(1)、(2)式组合统一后所得。
周维贤[7]通过计算分析了以上三种经验模型的适用范围,得出它们只适合于材料的应变硬化指数n值变化趋势呈单调增加或者单调减小的情况,不能完全描述n值出现拐点情况,故具有较大的局限性。为了解决以上矛盾,周维贤提出了描述硬化曲线的一种新经验关系模型(4),此模型已成功地描述了08Al钢应变硬化指数先增大后减小的硬化特性:

本文利用以上四种模型对不同加工状态(F、O、H1n、H2n、H3n)5052铝合金应变硬化行为进行非线性拟合,通过拟合结果残差平方和、相关系数的平方值R2检测法和应变指数n值的变化趋势检测法来共同评判应变硬化行为数学模型的准确性,从而能够更深入了解5052铝合金变形过程中应变硬化的变化规律。
1 实验材料及方法
实验材料采用西南铝业提供的5052 铝合金热连轧板材,两种厚度H规格分别为2.5mm和4.0mm,合金的化学成分为(质量分数,%):0.25Si,0.40Fe,0.10Cu,0.10Mn,2.2~2.8Mg,0.15~0.35Cr,0.10Zn,Al余量。
试验样品在西南铝业的单机架双卷取不可逆式轧机上进行冷轧工艺实验。冷轧后的样品采用气垫式退火炉、44T退火炉进行不同制度的退火工艺实验,从而获得不同加工状态下的合金板材。本文中的合金板材均通过控制冷轧与退火工艺制度(压下率、退火温度及退火时间等)以获得F-2.5、F-4.0、H16、H22、H24、H26、H34和O共8种强度级别,工艺流程如图1所示。注:“F-2.5”和“F-4.0”中的数字代表板材的厚度,未附带数字的板材厚度均为2.5mm。
依据GB/T228-2002标准,将试样板材加工成为标距50mm的标准试样,采用微机控制电子万能试验机(CMT5105)在室温下进行拉伸力学性能测试,应变速率έ=5×10-3/s,采集真应力和真应变等数据,再根据采集的数据找出表征材料加工硬化特性的参量。

图1 不同加工状态下的工艺流程图 (n=2,4,6)
2 实验结果及分析
2.15052 铝合金的应变硬化特征
图2为不同加工状态下5052铝合金板材应变硬化阶段的真应力-真应变曲线。从σ~ε图2a中可以看出不同加工状态下5052合金板材的硬化性能,其真应力水平H26>H16>H24>H34>H22>F2.5>O,F4.0。而在lnσ~lnε图2b中曲线的斜率即应变硬化指数n值随应变的增大呈先增加后减小的变化趋势,这与 Hollomon模型中n值为常数不相符,因此Hollomon模型并不能准确的描述该5052铝合金板材的应变硬化行为。

图2 不同加工状态下5052铝合金板材应变硬化阶段的真应力-真应变曲线
2.2 残差及相关系数平方和检验法
利用拟合结果的残差平方和Chi2/DoF值和相关系数平方R2值来检验(1)、(2)、(3)和(4)经验关系模型的参数拟合结果的准确性,当Chi2/DoF值越小,R2值越大,其拟合结果就越好。表1~表4列出了四种经验模型非线性拟合结果、残差平方和及相关系数平方R2值。对比表1~表4可知,模型(4)的残差平方和趋近于零,明显低于前三种经验模型;R2平均值模型(4)稍微高于另三种经验模型,模型(4)相对来说比较精确。但四种经验关系模型的参数拟合结果都具有较低的残差平方和及较高的相关系数平方值,因此若只考虑Chi^2/DoF值和R2值的大小,上述四种经验关系模型描述5052铝合金板材的应变硬化行为均已足够精确。

表1 模型σ=B(ε+ε0)N参数的非线性拟合结果及其残差平方和的均值与相关系数的平方值

表2 模型σ=B+CεN参数的非线性拟合结果及其残差平方和的均值与相关系数的平方值
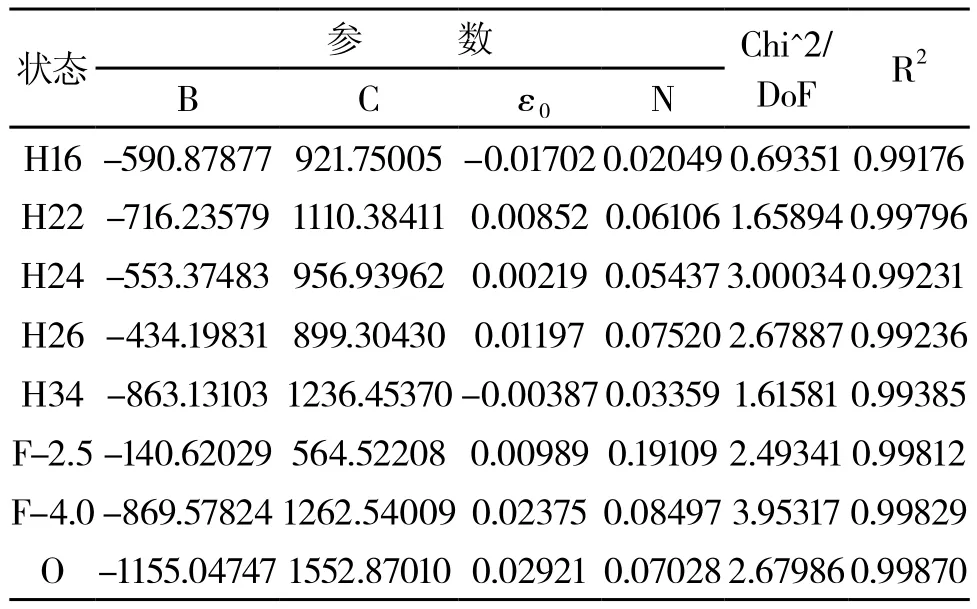
表3 模型σ=B+C(ε+ε0)N参数的非线性拟合结果及其残差平方和的均值与相关系数的平方值
表4 模型σ=参数的非线性拟合结果及其残差平方和的均值与相关系数的平方值
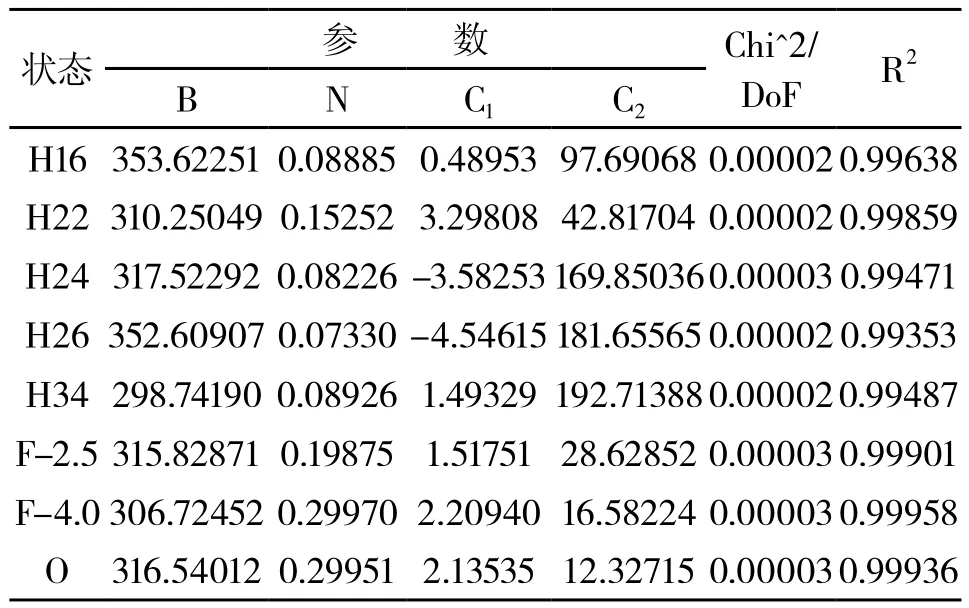
表4 模型σ=参数的非线性拟合结果及其残差平方和的均值与相关系数的平方值
状态 参 数 Chi^2/DoF R2 B N C1 C2 H16353.622510.088850.4895397.690680.000020.99638 H22310.250490.152523.2980842.817040.000020.99859 H24317.522920.08226-3.58253169.850360.000030.99471 H26352.609070.07330-4.54615181.655650.000020.99353 H34298.741900.089261.49329192.713880.000020.99487 F-2.5315.828710.198751.5175128.628520.000030.99901 F-4.0306.724520.299702.2094016.582240.000030.99958 O 316.540120.299512.1353512.327150.000030.99936
2.3 n值变化趋势检测法
通过文献[7、9、10]可以得知,材料的硬化特性是有差异的,有些材料的应变硬化指数n值随应变ε单调增加,有些则是单调减小的,有些则是先增后减亦或反之。因此,有必要通过n值的变化趋势来检测经验关系模型的准确性。由于模型(3)是模型(1)和(2)归纳统一后所得的通式:B=0时,即为(2)式;而ε0=0时,则对应(3)式。模拟结果准确性相对较高,所以这里只对模型(3)和模型(4)进行n值变化趋势检测来比较模型的准确度。
对表达式(3)求一阶导数得到:

应变硬化指数n随lnε的变化即为:
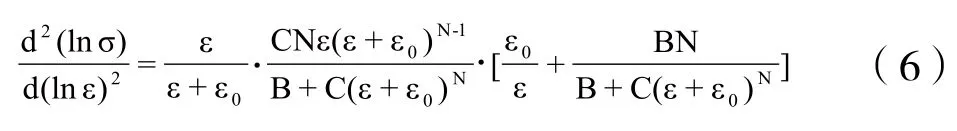
对表达式(4)求一阶导数得到:
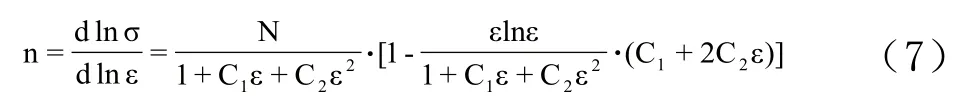
应变硬化指数n随lnε的变化即为:
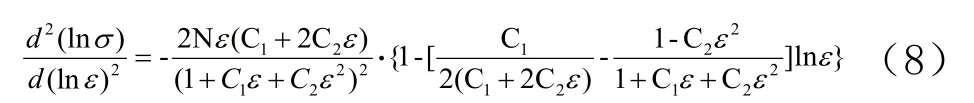
结合表3和表4中非线性拟合结果利用Origin软件对(5)~(8)式进行拟合得到不同加工状态下5052铝合金板材应变硬化曲线的一阶与二阶导数,即应变硬化系数n值及其随应变ε的变化规律,如图3和图4所示。由图2b可知,不同加工状态下合金板材的lnσ~lnε曲线的斜率并不是常数,而是随着应变ε增大而变化。当应变量较小时,lnσ~lnε曲线呈下凹特征;应变量达到一定值后lnσ~lnε曲线呈上凸特征,lnσ~lnε曲线的斜率(即应变硬化指数n值)表现出随着应变ε的增加表现出先增大后减小的变化趋势。此外,其一阶导数dlnσ/dlnε~lnε(或ε)曲线的峰值或二阶导数d2(lnσ)/d(lnε)2~lnε(或ε)曲线的零值应与双对数坐标下lnσ~lnε曲线的拐点相对应。
由图3可见,经过通式的经验模型(3)模拟后,5052合金板材只有在F-4.0和O状态下其一阶和二阶倒数能够反映出应变硬化指数n值出现拐点情况,其它状态下则不能够全面反映,故具有较大的局限性。而图4中则可以看到,所有加工状态下5052铝合金板材的应变硬化指数n值随应变ε的增大呈先增加后减小的变化趋势,并且dlnσ/dlnε~ε曲线的峰值与二阶导数d2(lnσ)/d(lnε)2~ε曲线的零值能够相对应。这说明了经验关系模型(5)可描述不同加工状态下5052铝合金板材应变硬化指数n值的变化趋势,可视为该合金应变硬化特征的最优模型。因此,不同加工状态下5052铝合金板材应变硬化方程如下所列:



图3 不同加工状态下5052铝合金板材应变硬化曲线的一阶与二阶导数特征
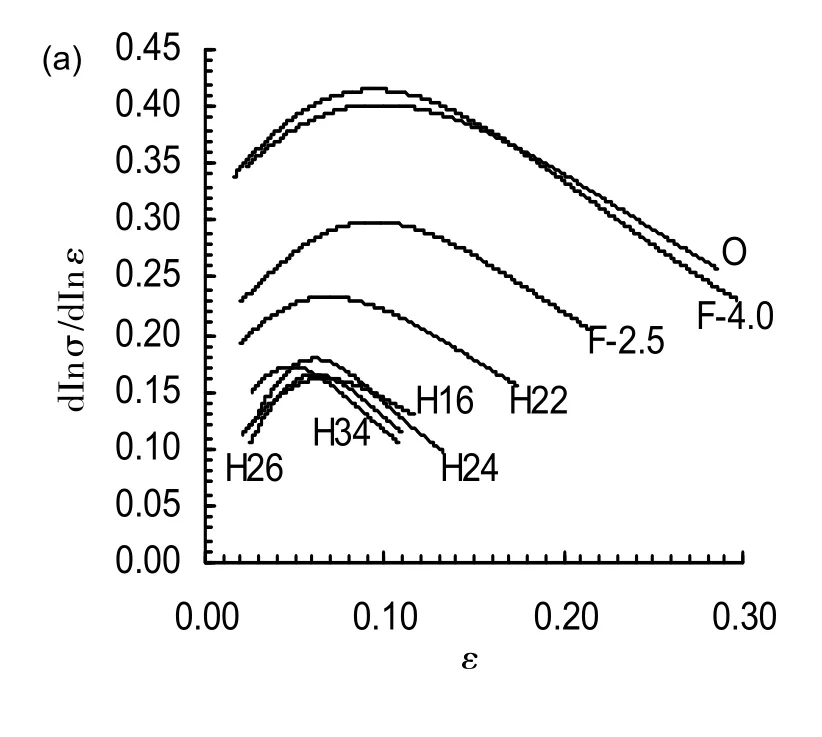

图4 不同加工状态下5052铝合金板材应变硬化曲线的一阶与二阶导数特征
3 结 论
(1)不同加工状态下5052铝合金板材应变硬化指数n随着应变的增加呈抛物线式曲线变化,并非恒定不变。
[1]肖亚庆主编.铝加工技术实用手册[M].北京: 冶金工业出版社, 2005.1, 第1版
[2]易成,关绍康,卢广玺,等.退火工艺对铸轧5052铝合金组织和性能的影响[J].材料热处理学报, 2011(32),4:52-57
[3]胡常云.5052H19合金薄板中间退火工艺研究[J].铝加工,2003(148),1:12-14
[4]莫德锋,何国求,胡正飞,等.铸造铝合金微观组织对应变硬化指数预测的影响[J].金属学报,2010(46),2:184-188
[5]黄明志, 骆竞晞, 贺保平.金属硬化曲线的阶段性和最大均匀应变[J].金属学报, 1983, 19 (4): A291-A299
[6]张旺峰, 陈瑜眉, 朱金华.亚稳态材料的应变硬化曲线与硬化参量[J].中国有色金属学报, 2000, 10 (Suppl.1): 236-238
[7]周维贤.描述钢板硬化曲线的一个新数模[J].材料科学进展, 1989, 3 (4): 325-330
[8]边舫,苏国跃,等.Inconel 718合金的加工硬化行为[J].有色金属,2005,57(1):1-3
[9]杨瑞成,夏渊,胡天雷.几种不锈钢的拉伸应变硬化行为[J].兰州理工大学学报,2011,37(1):5-9
[10]余海燕.金属薄板应变硬化模型比较分析[J].锻压技术,2012,37(5):1-6
