内压作用下圆柱壳周向斜接管结构设计分析

徐心怡，贺小华

(南京工业大学机械与动力工程学院，江苏南京 211816)

0 引言

圆筒形压力容器由于不同工艺操作的要求，常常需要在筒体上开设各种型式的接管。对于径向和轴向斜接管，国内外学者已经开展过大量研究工作［1－5］。薛明德等［6－8］基于精确的圆柱薄壳理论，给出了带径向接管圆柱壳的薄壳理论解并研究了该结构的弹性应力分析设计方法。周向斜接管结构应用广泛，但相对于径向和轴向斜接管结构，尚缺乏系统的设计方法研究。江楠［9］的试验结果表明，周向斜接管的应力集中系数随着非径向度的增加而增加，周向斜接管的最大应力大于径向接管。雷小刚等［10］采用三维有限元应力分析方法，计算带切向接管的圆筒形压力容器，并用电测试验对计算结果进行了验证，表明切向接管的最大应力集中系数低于相同尺寸径向接管的最大应力集中系数。王海峰等［11－12］对周向斜接管圆柱形容器进行了有限元分析，研究结果与RODABAUGH［13］的结论一致，即 ASME美国锅炉压力容器规范Ⅲ［14］中周向斜接管相对于径向接管的应力计算公式过大地估计了周向斜接管的最大弹性应力，是非常不准确的。

文中采用有限元法较为系统地计算了不同结构参数下受内压圆柱壳周向斜接管结构的弹性应力，绘制了不同开孔率 ρ(ρ=d/D)、开孔参数λ及接管壳体壁厚比 δet/δe下的等效薄膜及等效薄膜加弯曲应力集中系数Km，K图，并与GB 150—2011［15］中相应参数的径向接管结果进行对比，为周向斜接管结构设计和研究提供参考依据。

1 分析结构设计参数

1.1 几何模型结构

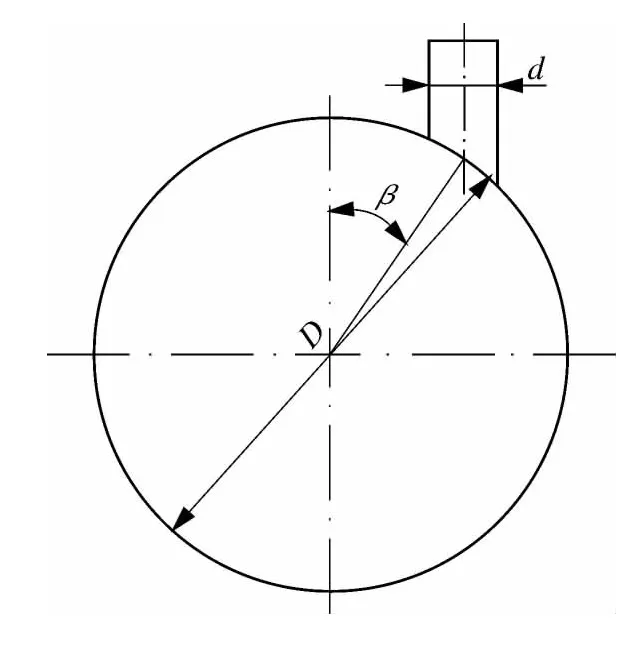
图1 几何模型结构

文中研究的是工程上较为常见的β=30°(β为周向斜接管倾角)的圆柱壳周向斜接管开孔结构，考虑到开孔造成的不连续效应的影响，模型壳体及接管具有足够长度，几何模型结构如图1所示，模型中考虑了实际焊接结构，焊接结构尺寸参照 HG/T 20583—2011［16］，见图2(图1，2中，D，d分别为壳体和接管的平均直径;δe，δet分别为壳体和接管的有效厚度)。

图2 壳体与接管焊接结构

1.2 材料性能

壳体材料选用压力容器专用钢板Q345R，接管材料选用20#钢。忽略温度的影响，弹性模量E=2.01 ×105MPa，泊松比 μ =0.3。材料的设计应力强度极限参照标准GB 150—2011《压力容器》［15］。

2 有限元分析

2.1 有限元模型

30°周向斜接管分析结构有限元的实体模型见图3。

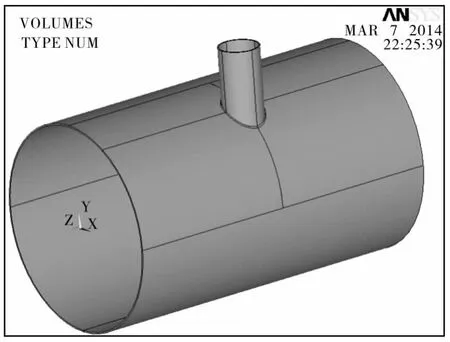
图3 30°周向斜接管结构有限元模型

单元选择20节点实体单元Solid 95，沿壳体及接管厚度3等分及以上，开孔接管处单元密度高。有限元模型的相贯区附近网格如图4所示。所有模型开孔区远离壳端边缘效应区。载荷及边界条件为:壳体一端施加全约束，结构内表面施加设计压力，壳体另一端面及接管端面施加轴向平衡力。

图4 有限元模型相贯区网格与线性化路径

2.2 计算方案

参照 GB 150—2011《压力容器》［15］圆柱壳径向接管的设计图6－13，考虑到接管与壳体相切时，其极限倾角 β=arcsin(1－d/D)，当 β=30°时，最大开孔率ρ=0.5，文中各分析模型选取开孔率 ρ=0.1，0.2，0.3，0.4;接管壳体壁厚比 δet/δe=0.5～2，开孔参数 λ =0.7～12，与 GB 150—2011［15］中图6－13 保持一致。

2.3 有限元计算结果

对β=30°圆柱壳周向斜接管开孔结构在内压作用下进行了弹性应力分析，找出分析结构各计算模型的应力最大值点，针对各线性化路径A－A，B－B及C－C进行应力线性化处理，得出最大等效薄膜应力Sm及最大等效薄膜加弯曲应力S，根据等效应力计算公式，得到等效薄膜应力集中系数Km及等效薄膜加弯曲应力集中系数K:

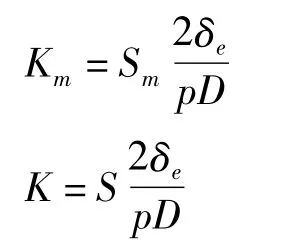
表1列出了部分开孔率为0.1时β=30°圆柱壳周向斜接管结构Km，K的三维有限元解。开孔率为0.2～0.4的应力强度有限元数值解见文中所绘制的等效应力集中系数曲线图。

表1 部分模型等效薄膜应力集中系数Km和等效薄膜加弯曲应力集中系数K的三维有限元解

(续)

根据三维有限元计算结果，作出不同开孔参数ρ，λ及壁厚比 δet/δe下的等效应力集中系数Km，K 图，如图5～8所示。

图5 ρ=0.1的等效薄膜应力集中系数Km图和等效薄膜加弯曲应力集中系数K图

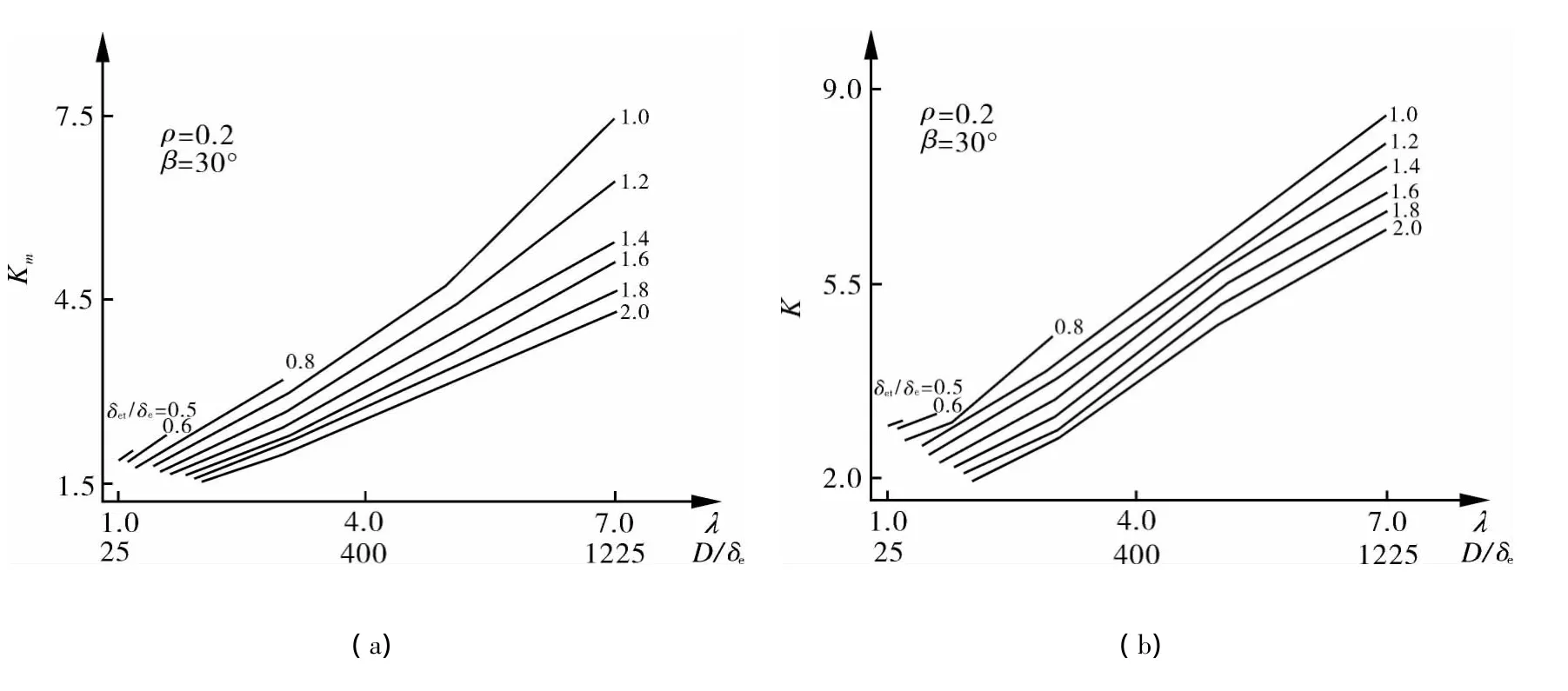
图6 ρ=0.2的等效薄膜应力集中系数Km图和等效薄膜加弯曲应力集中系数K图

图7 ρ=0.3的等效薄膜应力集中系数Km图和等效薄膜加弯曲应力集中系数K图

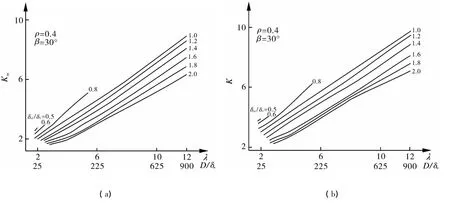
图8 ρ=0.4的等效薄膜应力集中系数Km图和等效薄膜加弯曲应力集中系数K图

3 分析讨论

3.1 分析结果验证

为验证文中分析模型所得等效应力集中系数曲线的可信度，取某开孔率及壁厚比参数下本文径向接管(β=0°)三维有限元计算解，并分析得到各参数下的等效应力集中系数，与GB 150—2011中的薄壳理论解对应的设计曲线进行比较，比较结果如图9所示。可以看出，基于本文有限元解的等效薄膜应力集中系数Km与基于GB 150—2011薄壳理论解的结果吻合得非常好;等效薄膜加弯曲应力集中系数趋势一致，在开孔系数λ较小及较大时，两者存在一定差异。其原因可能是薄壳理论解分析的接管对象没有考虑真实焊缝结构，理论解简化的假设与有限元解的差异导致而成。薛明德等［17］在其文中列举的部分有限元模型解与薄壳理论解也存在一定差异。图9的分析比较结果表明，文中各分析模型的计算结果是较为可靠的。

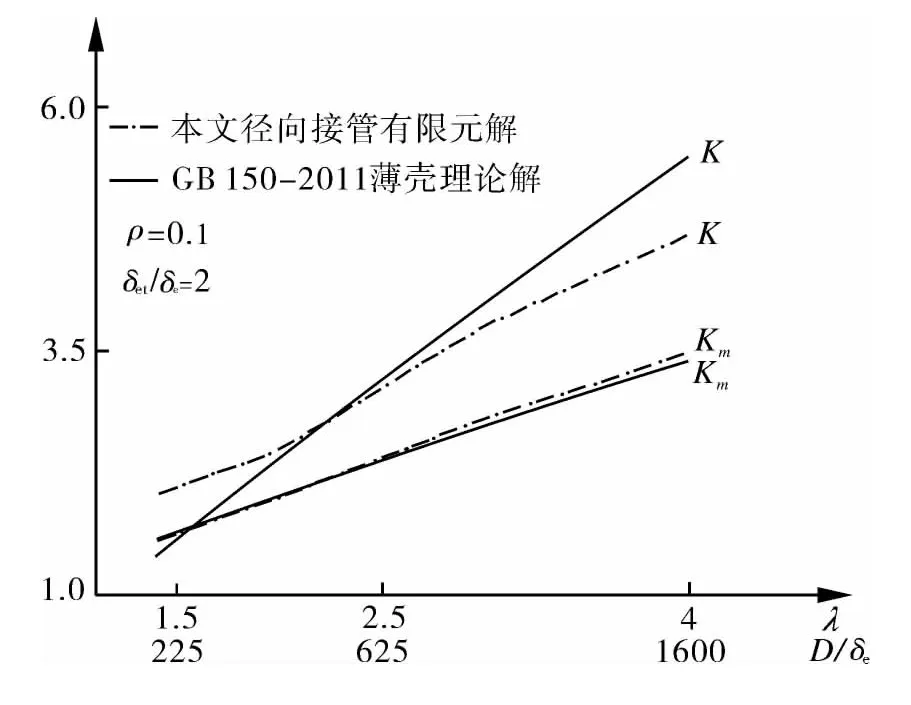
图9 径向接管Km，K曲线比较

3.2 周向斜接管与径向接管分析结果比较

图10示出了开孔率ρ=0.1，接管壳体壁厚比δet/δe=1.0下径向接管及周向斜接管结构的Km，K 曲线，虚线为基于 Mershon 公式［18］Sβ=S0(cosβ)0.5(式中，Sβ和 S0分别为周向斜接管结构与径向接管结构的最大弹性应力)得出的曲线。由图10可以看出，与径向接管相比，周向斜接管结构的等效薄膜应力集中系数及等效薄膜加弯曲应力集中系数均偏小，等效薄膜加弯曲应力集中系数的差异较之于等效薄膜应力要小得多。开孔参数λ较小时，Mershon公式得到的Km，K与本文有限元解较为接近，而随着开孔参数 λ的增大，二者差异逐渐显著。

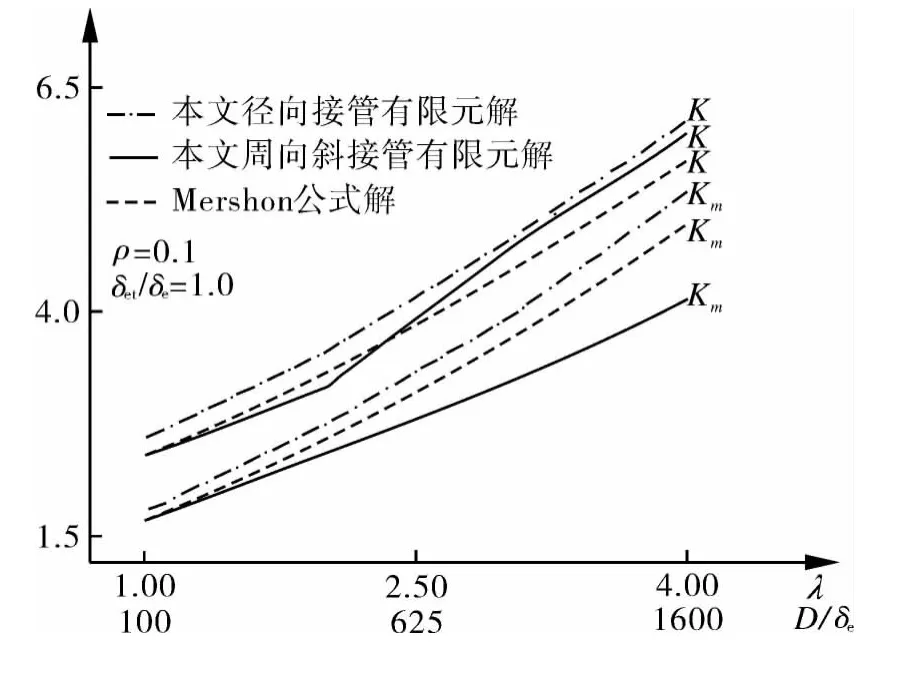
图10 Mershon公式解与本文径向及斜接管解曲线

4 结论

(1)本文计算参数范围内，内压下圆柱壳周向斜接管结构的等效薄膜应力及等效薄膜加弯曲应力集中系数均低于同参数时的圆柱壳径向接管结构，等效薄膜应力的差异较为显著。

(2)当开孔参数λ较小时，基于有限元的周向斜接管等效应力集中系数解与Mershon公式较为接近，随着λ增大，二者差异逐渐显著。

(3)绘制了β=30°周向斜接管结构的等效应力集中系数曲线，可为该种结构的工程设计提供依据。

［1］BIJLAARD P P.Stresses form radial loads and external moments in cylindrical pressure vessels［J］.Welding Research supplement，1995，34(12):608－617.

［2］KOVES W J，SANGER R J.Evaluation of pressure design criteria foe nozzles［C］//International Conference on Pressure Vessel Technology，Dusseldorf，Canada，Kent，1996:271－279.

［3］UPDIKE D P，KALNINS A.Tensile plastic instability of axisymmetric pressure vessels［J］.ASME Journal of Pressure Vessel and Technology，1998，120(2):6－11.

［4］林杨杰，桑芝富.具有30°斜接管内压容器极限载荷的有限元分析［J］.压力容器，2000，17(3):24－28.

［5］SANG Z F.Limit and burst pressure for a cylindrical shell intersection with intermediate diameter ratio［J］.International Journal of Pressure Vessels and Piping，2002，79(4):341－349.

［6］杜青海，薛明德.内压下带径向接管圆柱壳的薄壳理论解［J］.清华大学学报(自然科学版)，2008，48(2):264－269.

［7］薛明德，杜青海，黄克智.圆柱壳开孔接管在内压与接管外载作用下的分析设计方法［C］//压力容器先进技术——第七届全国压力容器学术会议论文集.江苏无锡，2009:302－312.

［8］薛明德，杜青海，黄克智.内压作用下圆柱壳开孔接管的分析设计方法［J］.压力容器，2007，24(6):17－24.

［9］江楠.圆筒形压力容器上不同接管型式的实验研究［J］.化工设备设计，1995(1):8－11.

［10］雷小刚，黄克敏.圆筒形压力容器切向接管的三维有限元分析［J］.石油化工设备，1993(1):13－17.

［11］王海峰，桑芝富.周向斜接管内压容器的有限元分析［J］.压力容器，2005，22(5):16－19.

［12］王海峰，桑芝富.周向斜接管内压圆柱形容器的应力集中［J］.石油机械，2005，33(11):11－14.

［13］RODABAUGH E C.Code Rules for Internal Pressure Design of Isolated Nozzles in Cylindrical Vessels with d/D≤1.0［R］.Welding Research Bulletin No.451，2000.

［14］ASME Boiler and Pressure Vessel Code.Section Ⅲ，Division 1［S］.American Society of Mechanical Engineers，New York，1998.

［15］GB 150—2011，压力容器［S］.

［16］HG/T 20583—2011，钢制化工容器结构设计规定［S］.

［17］薛明德，黄克智，李世玉，等.GB 150—2011中圆筒开孔补强设计的分析法［J］.化工设备与管道，2012，49(3):1－11.

［18］MERSHON J L.Interpretive Report on Oblique Nozzle Connections in Pressure Vessel Heads and Shells under Internal Pressure Loading［R］.Number 153，Welding Research Council Bulletin，Aug 1970.