ANSYS极限载荷分析法在压力容器设计中的应用

白海永，方永利

(哈尔滨电气股份有限公司，黑龙江哈尔滨 150046)

0 引言

基于不同的失效形式，压力容器设计分为常规设计和分析设计。其中分析设计又有基于弹性应力分析的应力分类法、极限载荷分析法和弹－塑性应力分析法。在分析设计法进入工程设计实践以来，已被广泛应用的设计方法是基于弹性应力分析的应力分类法。

1 弹性应力分析法

压力容器应力分析设计规范ASMEⅧ－2和JB4732—1995(2005 年确认)［1］要求将应力进行分类，分为:一次总体薄膜应力Pm，一次局部薄膜应力PL，一次弯曲应力Pb，二次应力Q和峰值应力F。然后分别应用不同的安全限值对以上应力分类或其组合进行应力评定。但在应用有限元方法分析计算中只能给出结构中各处总应力的计算结果，如何将总应力分解成上述5类应力是国内外压力容器研究的热点，并已经取得了重要的进展。对于一次总体薄膜应力Pm，一次局部薄膜应力PL，一次弯曲应力Pb，峰值应力F的判别已基本达成了统一的规范性建议。然而对于如何将等效线性化处理得到的薄膜加弯曲应力进一步分为一次应力或二次应力，则是国内外压力容器领域关注的热点。如果简单地将其定性为一次应力，则会保守的将二次应力成分定性为一次应力成分，这种保守的处理方法有时会导致结构应力评定不合格，从而非常保守地改变设计结构与设计尺寸，造成经济上的浪费;相反，如果将其定义为二次应力，则冒进地将一次应力成分定义为二次应力，这样的设计结构有可能会造成灾难性的后果。那么如何处理薄膜加弯曲应力中的一次成分和二次成分，从而平衡设计的经济性和安全性，就成为了分析设计中的重要问题。

对于以上情况，有学者提出了几种解决方案，如一次结构法［2－7］:该方法的基本思想是认定机械载荷引起的二次应力与总体结构不连续性有关，不连续位置通过变形协调来保证结构的连续性，由此导致二次应力。一旦此约束解除，相应的二次应力就会消失，同时结构将会出现不连续性。如果该约束解除后的新结构还能继续承载，则证明消失的那部分应力不属于平衡外部机械载荷所需要的一次应力，可以归入二次应力。如果新结构中还有高应力，重复上述解除相应约束的过程。如此继续，直到新结构变成不能承受外部机械载荷的可动机构或新结构内的应力已能满足一次应力强度的评定准则为止，这就是一次结构法的基本思想，这些解除约束后得到的新结构统称为“一次结构”。一次结构法可以对薄膜加弯曲应力成分进一步进行区分，将经过检验确定是二次应力成分的逐一剔除，剩余部分作为一次应力，从而应力分类问题可以得到很好地解决。然而一次结构法在实际应用过程中相对较复杂，增加了设计过程的复杂性与不确定性。

2 极限载荷分析法

ASMEⅧ－2—2010中对应力分类法与极限分析法的使用进行了详细说明，通过应力分类法确定的总体薄膜应力、局部薄膜应力以及一次薄膜加一次弯曲应力应满足规范的限值要求，可防止塑性垮塌，此方法是一种近似解。而极限分析法是应力分类法的一种替代方法，可以得到较为精确的判断，即:满足极限分析的要求时，不需评定一次应力，一次应力的限值自动满足。

极限载荷分析涉及塑性破坏的失效模式以及结构的总体塑性变形(塑性垮塌)的开始。它适用于以任何规定的顺序施加的单一或多种静载荷。

极限载荷分析是基于极限分析理论，旨在防止塑性垮塌，对结构的极限载荷规定一个下限值，并结合以下性能，作为数值模型解:(1)材料模型:采用规定屈服强度的全塑性(应以屈服强度等于1.5Sm来确定塑性极限)，应用von Mises函数和关联流动法则;(2)应变—位移关系:小位移理论的应变—位移关系;(3)在不变形的结构形状中满足平衡关系［8］。

极限载荷分析采用数值分析技术(如有限元方法)并结合弹性－全塑性材料模型以及小位移理论，以求得极限载荷。极限载荷是引起总的结构失稳的载荷，在有限元分析中，此值可以通过多个载荷步、小的载荷增量来确定。达到极限载荷的特征是:结构的某个截面失去了平衡，即发生了塑性垮塌［9］。

3 极限载荷分析法的ANSYS实现

图1 结构三维图

以某压缩空气储罐为例，设计压力1.2 MPa，设计温度70℃，介质为压缩空气，封头有φ103 mm接管开孔。受内压载荷的封头组件为轴对称结构，简化为二维轴对称模型。封头和接管内侧施加内压载荷，接管端部施加等效压力载荷，筒体模型下侧施加轴向位移约束。有限元单元类型为Plane 183单元，结构形式如图1所示，有限元模型载荷施加如图2所示。

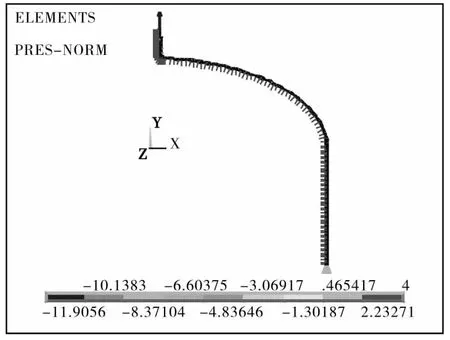
图2 有限元载荷施加图

文中通过3种方法求解结构的极限载荷，并对3种方法进行对比，从而确定最优的设计方法。

3.1 第1种方法

极限载荷分析为材料非线性［10］问题，因此，为了保证数值解的稳定性，对网格划分要求较高。分析材料设置BISO(双线性各向同性强化材料选项)，屈服准则为von Mises准则。根据ASME规范，要求数值分析中使用全塑性材料模型，因此设置切向模量为0。材料属性如图3所示。

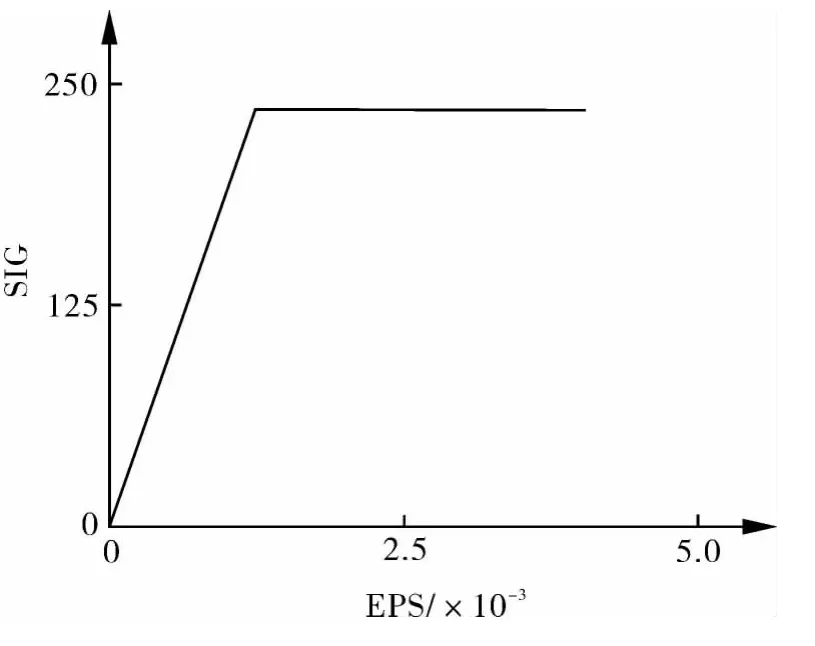
图3 BISO材料属性曲线

根据ASME规范，可以通过小载荷增量，确定不能满足平衡的解，以确定极限载荷。当载荷使结构达到极限载荷时，结构变为几何可变结构，几何可变结构可能是整体的也可能是局部的。通常在接近极限载荷时，将载荷增量设置得足够小，以保证求解精度。ANSYS处理非线性问题包括多载荷步、自动时间步长等技术。随着计算机软硬件的快速发展，以及高性能多线程计算方法的出现，大大简化了设计工作，因此本案例每个载荷步的增量取0.001 MPa。

在求解过程中，当载荷达到极限载荷值时，模型变成几何可变结构，求解发散，ANSYS会出现错误提示，这些错误提示可帮助用户判断结构的极限载荷。

通过ANSYS时间历程后处理模块POST26，可获得载荷—应变曲线及其函数关系。通过PRVAR命令可以获得极限载荷值为2.692 MPa，塑性极限载荷的2/3(1.79 MPa)大于给定载荷(1.2 MPa)，符合规范的要求，不需要评定一次应力。

对确定的极限载荷的验证:将内压设置为2.692 MPa时，结构可以获得有限元解;而将内压增大0.001 MPa，即设置为2.693 MPa 时，结构有限元解不收敛，因此，结构的塑性极限载荷为2.692 MPa。

3.2 第2种方法

当载荷以小增量增大到极限载荷时，结构变为可变结构，对于常规求解方法，有限元解将发散，如第1种方法计算过程。ANSYS提供了多种用于求解不稳定问题的技术，弧长法便是其中一种方法，该方法可以处理整体不稳定问题;更重要的是，可以模拟负载荷位移斜率曲线。弧长法可以得到许多物理不稳定结构的数值稳定解。

应用弧长法需要注意以下几点:(1)弧长法仅限于比例结构载荷(斜坡载荷)的静力分析;(2)程序根据第一个子步的第一次迭代的载荷(或位移)增量计算参考弧长半径;(3)应用弧长法时，线性搜索、预测、自适应下降、自动时间步长及时间积分效应均无效;(4)弧长法可能会得到负的刚度。

弧长法可以将分析扩展到后屈曲范围。使用该特征可以跟踪“载荷—变形”曲线发生“阶跃”或“回跃”响应的区域。

图4示出，当载荷增大到极限载荷后，结构变为可变结构，即:载荷不变、位移无限增大，得到极限载荷为 2.690 MPa。

应用弧长法需要注意，只有当作用载荷上的解收敛或达到ARCTRM命令设定的限值时，弧长法求解才会终止。因此对于可变结构，需要通过ARCTRM设置终止求解条件。

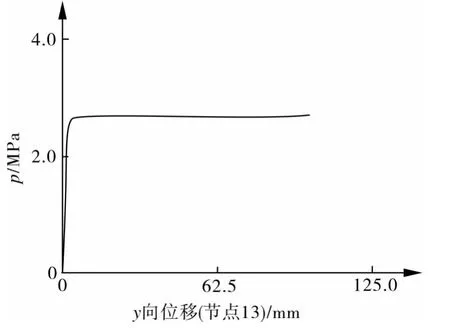
图4 弧长法节点位移—载荷曲线

3.3 第3种方法

通过给定切变模量，可以使载荷增量达到极限载荷后继续求解，即结构经过弹塑性变形阶段后并不表现为理想全塑性。

图5示出弹塑性分析法节点位移—载荷曲线，图6示出结构经过弹塑性变形阶段局部放大位移—载荷曲线。使用清华大学提出的0曲率法［11］确定极限载荷为 2.69 MPa。

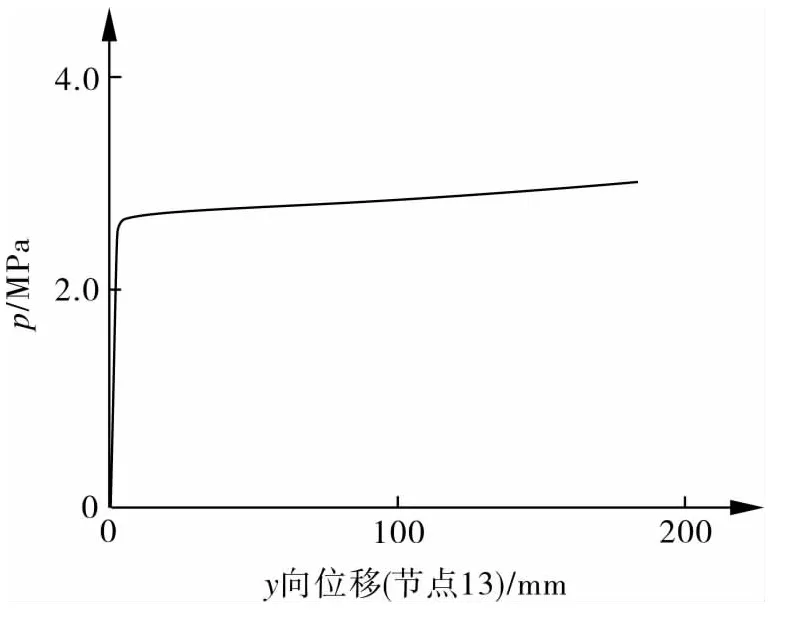
图5 弹塑性法节点位移—载荷曲线1

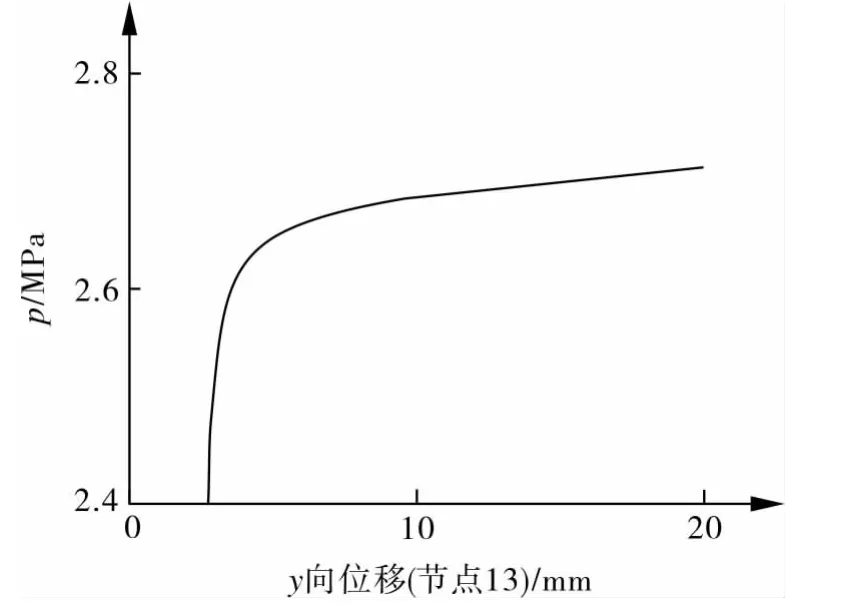
图6 弹塑性法节点位移—载荷曲线2

由以上3种方法可以看出:

(1)弧长法需要设定载荷步数NSBSTP来改变参考半径;弹塑性法需要给定相对小的切变模量，且极限载荷的确定有不精确性;

(2)与另两种方法比较，第1种方法计算结果准确，且操作简单，建议采用。

4 结语

极限载荷分析法是对基于弹性分析的应力分类结构评定法的合理补充，从而有效地弥补了应力分类结构评定法的不足，必将在以后的压力容器设计工程实践中得到充分的发展和广泛的应用。

［1］JB 4732—1995，钢制压力容器——分析设计标准(2005年确认)［S］.

［2］李建国.JB 4732—1995《钢制压力容器——分析设计标准》培训教材［M］.全国压力容器标准化技术委员会.

［3］陆明万，徐鸿.分析设计中若干重要问题的讨论(二)［J］.压力容器，2006，23(2):28－32.

［4］陆明万，寿比南，杨国义.压力容器分析设计的塑性分析方法［J］.压力容器，2011，28(1):33－39.

［5］LU Mingwan，LI Jianguo.Primary structure－an important concept to distinguish primary stress，Seismic Engineering［C］.ASME PVP，1996.

［6］LU Mingwan，CHEN Yong，LI Jianguo.Two－step approach of stress classification and primary structure method［C］.Journal of PV Technology，2000.

［7］李建国.压力容器设计的力学基础及其标准应用［M］.北京:机械工业出版社，2004.

［8］ASME Boiler ＆ Pressure Vessel Code－2010，Ⅷ Division 2，Alternative Rules，Rules for Construction of Pressure Vessels［S］.

［9］沈鋆.极限载荷分析法在压力容器分析设计中的应用［J］.石油化工设备，2011，40(4):35－38.

［10］同济大学航空航天与力学学院基础力学教学研究部.材料力学［M］.上海:同济大学出版社，2005.

［11］ZHANG W M，LU M W，ZHANG R Y.A zero－curvature criterion to determine the practical collapse load［C］.PV Technology，Voll.ICPVT6，Beijing，1988.