舰船壳体模块感应磁场的等效计算

张安明，陈文涛，虞伟乔，郭成豹

1 海军驻大连船舶重工集团有限公司军事代表室，辽宁大连 116005

2 中国人民解放军91656部队，上海 200231

3 海军工程大学电气与信息工程学院，湖北武汉 430033

0 引 言

舰船大多由钢材建造，在地球磁场的作用下将被磁化，其周围会产生感应磁场。为提高舰船的磁性防护能力，需正确获得感应磁场的数值，以设计出优良的舰船消磁系统。

在舰船建造之前，很难得到舰船的感应磁场，主要采取两类手段：建造磁性物理模型和数学模型。建造磁性物理模型可以得到较准确的舰船磁场，但由于机械加工等方面的原因，建造过程很长，并且无法灵活地修改模型结构。因此，目前发展了很多种数值化技术以建立舰船磁性的数学模型，主要包括有限元法（FEM）［1］、边界元法（BEM）［2］以及磁矩量法（MMM）［3-8］等。应用MMM法计算舰船磁场，其主要优点在于所需剖分的场源能够做到单元数比FEM少，而算法又比BEM容易实现，计算结果最直观。但该方法的最大缺点就是所需计算机资源会随着单元数目的增长而呈指数增加［8］，限制了该方法的推广应用。虽然有些文献［3-7］采用等效体积磁化率的概念将舰船结构等效为钢质实心体进行了计算，但也只能得到一些较为粗略的计算结果，误差较大。随着计算机硬件和磁场计算技术的发展，已经可以实现较大复杂度的磁矩量法计算［8］，只是鉴于舰船结构的复杂性，仍然需要采取一定的磁等效技术来简化舰船结构。

本文主要针对舰船结构的最基本元素——舰船壳体模块，采用横截面积与磁化率乘积相等的原则，将由薄钢板和肋骨组成的结构复杂的舰船壳体模块等效、简化为一个各向异性的薄钢板结构，并采用MMM法分别计算简化前、后结构的感应磁性，通过对计算结果的对比，分析这种等效方法的可行性。

1 舰船壳体模块的磁性等效

1.1 舰船壳体模块的磁化特点

如图1所示，一个舰船壳体模块，其磁导率很高（μr＞0），厚度t远小于它的宽度w和长度L，以至于从局部来看（例如，数值计算中剖分单元尺度范围），舰船壳体的磁场决定于磁化率 χ与厚度t的乘积 χ t［9-11］。严格来说，铁磁材料的磁化率χ不是常数，而是磁场H的函数，即 χ=f(H)。由于引起舰船磁化的外界磁场主要是地磁场，在这种弱磁场的作用下，舰船壳体所用铁磁材料的磁化率 χ可以认为是常数，从而可以认为舰船感应磁场的幅值与地磁场的大小成线性关系。

1.2 横截面积与磁化率乘积相等的磁性等效

舰船壳体主要由薄钢板和肋骨构成，其结构和铁磁物质分布复杂，难以适合数值计算上的数据处理，尤其不适合MMM等对剖分单元数目具有严格限制的计算方法。

由于要计算的舰船磁场离船体较远，因而采取磁性等效的措施以简化数据处理是可行的［12］。由于舰船壳体的磁场决定于其磁化率与厚度的乘积，因此，可以采用横截面积与磁化率乘积相等的原则，将由薄钢板和肋骨组成的结构复杂的舰船壳体模块等效，简化为一个各向异性的薄钢板结构。

根据相似性定理，磁化情况相同、几何结构相似的铁磁物体产生的磁场相同，因此要建立舰船壳体的磁性等效关系，需要建立如下两个相似性条件：

1）横截面积相等。如果等效后舰船壳体的横截面积为Sm，横截面积相似表述方程为

式中，Sf为等效前舰船壳体的横截面积。

2）横截面积与磁化率乘积相等。如果等效后舰船壳体的横截面积为Sm，磁化率为χm，那么它们的乘积可以表述为相似性方程：

式中，χf为等效前舰船壳体的磁化率。

图2所示为一个舰船壳体垂直于肋骨方向的横截面。由于肋骨部分的长度尺度是高度和厚度尺度的10倍，甚至是100倍，因此肋骨在长度方向容易磁化，而在高度和厚度方向则不容易磁化。因此在进行磁性等效时，在肋骨长度方向上需要考虑肋骨的影响，而在肋骨高度和厚度方向则不需考虑肋骨的影响。假设：薄钢板部分的横截面积为Sf1，磁化率为χf1；肋骨部分的横截面积为Sf2，磁化率为χf2；等效后的薄钢板结构的横截面的厚度为e，宽度为w，等效后的横截面积为Sm=ew。那么，按式（2）所示的磁化率与横截面积乘积相等的条件，可以得到平行于肋骨方向的舰船壳体长度方向的等效磁化率 χm为

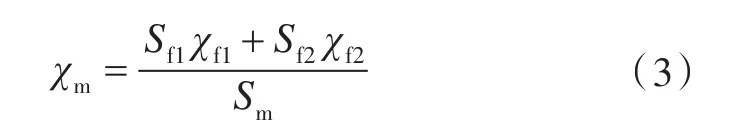
而垂直于肋骨长度方向的舰船壳体宽度方向、厚度方向的等效磁化率则仍取薄钢板部分的磁化率值，即 χm=χf1。

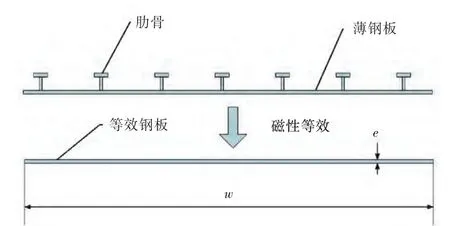
图2 等效前、后的舰船壳体横截面Fig.2 A ship hull section before and after equivalent

2 磁矩量法三维磁场计算原理

场域中的铁磁物体，在激励磁场作用下被磁化，通过磁化物质的标量位可以求得磁化物质产生的磁场强度

将铁区分为小块单元，则单元内的磁化强度可视为常数，各单元的磁场强度为

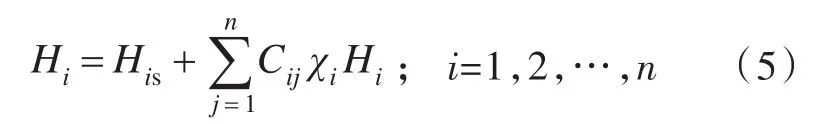
式中：Hi｛Hix，Hiy，Hiz｝为各单元磁场强度的分量；His｛Hisx，Hisy，Hisz｝为磁化磁场在i单元位置处产生的磁场强度的分量；Cij为j单元对i单元的耦合张量，磁场强度只与单元的几何尺寸以及单元与场点之间的距离有关。

3 数值算例

3.1 算例参数

如图3所示，一个舰船壳体模块由1块薄钢板和5根肋骨组成。其中，薄钢板长500 mm，宽500 mm，厚2 mm，磁化率为150；间隔124 mm均匀分布在薄钢板上的5根肋骨尺寸相同，长500 mm，宽4 mm，高10 mm，磁化率为100。

图3 舰船壳体模块的横截面Fig.3 The cross section of a ship hull module

按照上述磁性等效方法，假设等效钢板的厚度为2 mm，那么在长度方向的等效磁化率为170，宽度方向的等效磁化率为150，厚度方向的等效磁化率为150。

3.2 计算结果

假设上述舰船壳体模块处于长度方向的磁场在Bx=34300 nT的作用下，采用磁矩量法进行磁性建模，并计算外部一条计算线上的感应磁场。如图4所示，计算线长2000 mm，位于模块x方向的对称平面上，与模块的垂直距离为500 mm（垂直方向为z方向）。

图4 计算线的位置Fig.4 The position of the calculation line

计算按照磁性等效前与等效后两种模式进行。其中等效前的单元划分方案如图5所示，包括150个单元；等效后的单元划分方案如图6所示，包括100个单元。两种计算模式的计算结果分别如图7和图8所示。

图5 等效前的单元划分Fig.5 The element partition before equivalent

图6 等效后的单元划分Fig.6 The element partition after equivalent

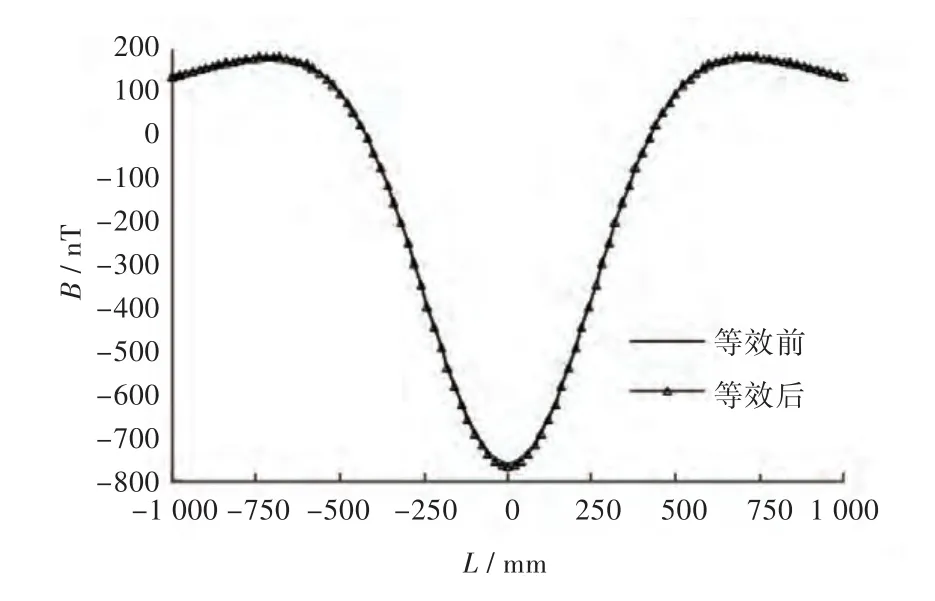
图7 x分量计算值Fig.7 The x component of the calculation result

图8 z分量计算值Fig.8 The z component of the calculation result

3.3 分 析

从图7和图8可以看出，等效前、后的磁场计算结果具有很好的一致性，峰值误差不超过1.5%。等效后的计算所需要的单元数目少于等效前的（减少1/3），并且简化了舰船壳体的结构建模工作量，这对于磁矩量法计算非常有意义。

需要特别指出的是，本例中垂直于肋骨方向的舰船壳体宽度方向、厚度方向的等效磁化率因仍取薄钢板部分的磁化率值150，且其对于舰船壳体感应磁场的影响亦不大于1.5%，因而可忽略不计，在此不再详述。

4 结语

本文采用横截面积与磁化率乘积相等的原则，将由薄钢板和肋骨组成的结构复杂的舰船壳体模块等效，简化为一个各向异性的薄钢板结构，并采用磁矩量法分别计算了简化前、后结构的感应磁场。通过对比计算结果，可以发现这种磁性等效具有很高的计算精度。这种等效技术有利于简化数据准备工作，并且可以减少单元数目，是计算舰船壳体感应磁场的一条切实可行的途径。

［1］BRUNOTTE X，MEUNIER G，BONGIRAUD J P.Ship magnetizations modeling by the finite element method［J］.IEEE Transactions on Magnetics，1993，29（2）：1970-1975.

［2］RIOUX-DAMIDAU F，BANDELIER B，PENVEN P.A fast and precise determination of the static magnetic field in the presence of thin iron shells［J］.IEEE Transactions on Magnetics，1995，31（6）：3491-3493.

［3］倪振群，蔡雪祥，翁行泰.舰船主甲板模型感应磁场的计算［J］.上海交通大学学报，1996，30（7）：83-88.NI Zhenqun，CAI Xuexiang，WENG Xingtai.Computation of inductive magnetic field induced by vessel's main deck model［J］.Journal of Shanghai Jiaotong University，1996，30（7）：83-88.

［4］蔡雪祥，倪振群，翁行泰.舰船上层建筑模型的等效磁化率研究［J］.上海交通大学学报，1996，30（7）：89-94.CAI Xuexiang，NI Zhenqun，WENG Xingtai.The study of equivalent susceptibility of the superstructure model of a vessel［J］.Journal of Shanghai Jiaotong University，1996，30（7）：89-94.

［5］蔡雪祥，翁行泰，倪振群.舰船主甲板模型感应磁场计算中等效磁化率的应用［J］.上海交通大学学报，1996，30（9）：81-85.CAI Xuexiang，WENG Xingtai，NI Zhenqun.Application of equivalent susceptibility in the computation of inductive magnetic field of the main deck model of a vessel［J］.Journal of Shanghai Jiaotong University，1996，30（9）：81-85.

［6］郭成豹，何明，周耀忠.积分方程法计算舰船磁场［J］.海军工程大学学报，2001，13（6）：71-74.GUO Chengbao，HE Ming，ZHOU Yaozhong.The Calculation of induced magnetic fields of ships by integral equation method［J］.Journal of Naval University of Engineering，2001，13（6）：71-74.

［7］郭成豹，刘大明，朱宝成.潜艇感应磁场的三维积分方程法数值计算研究［J］.海军工程大学学报，2002，14（3）：41-44.GUO Chengbao，LIU Daming，ZHU Baocheng.Research on the numerical calculation of submarine induced magnetic fields by integral equation method［J］.Journal of Naval University of Engineering，2002，14（3）：41-44.

［8］郭成豹，刘大明.薄钢壳物体磁特征建模研究［J］.兵工学报，2012，33（8）：912-915.GUO Chengbao，LIU Daming.Modeling of magnetic signatures of thin sheet objects［J］.Acta Armamenta-rii，2012，33（8）：912-915.

［9］ESKOLA L，PURANEN R，SOININEN H.Measurement of magnetic properties of steel sheets［J］.Geophysical Prospecting，1999，47（4）：593-602.

［10］ESKOLA L，JOKINEN T，SOININEN H，et al.Some remarks on static field thin sheet models［J］.Journal of Applied Geophysics，1993，30（3）：229-234.

［11］CHADEBEC O，COULOMB J L，LECONTE V，et al.Modeling of static magnetic anomaly created by iron plates［J］.IEEE Transaction on Magnetics，2000，36（5）：667-671.

［12］AURIAULT J L.Heterogeneous medium：Is an equivalent macroscopic description possible？［J］.International Journal of Engineering Science，1991，29（7）：785-795.