减摇鳍与船体的适配性数值模拟

吉明，叶青云，袁聪

哈尔滨工程大学自动化学院，黑龙江哈尔滨 150001

0 引 言

目前，国内的很多研究都只讨论了孤立的减摇鳍在敞水中（或称在均匀流场中）的水动力性能［1］，或者只研究了孤立的船体（即不带任何附体）在静水中航行时的水动力特性［2］。而实际减摇鳍是在船体的两侧工作，以让减摇鳍和船体成为一个系统，因此两者之间必然存在相互作用。这种相互作用表现为船体所形成速度场与减摇鳍所形成速度场之间的相互影响［3］。在船体两侧工作的减摇鳍受船体的影响，作用于鳍翼表面的水流速度及其分布情况与敞水者不同，为了研究两者之间的异同以及减摇鳍与船体的适配性问题，本文将利用商业 CFD软件 FLUENT［4］，采用 SIMPLE算法和二方程湍流模型RNG k-ε数值模拟静态时敞水条件下的减摇鳍与受船体约束减摇鳍的水动力特性，以及动态时中、高航速和零航速敞水条件下减摇鳍与受船体约束减摇鳍的水动力特性。并通过计算对比分析加了船体后对减摇鳍升力、阻力及力矩的影响，分析敞水条件下减摇鳍与加了船体后的减摇鳍所表现出的水动力特性差异的原因。

1 计算流体力学数值模拟

1.1 几何模型的建立

本文采用低航速水翼的几何参数，水翼面积为4 m2，翼型为NACA64系列。为了简化模型，船体采用的是某型驱逐舰0～17站的船型型值表数据，并且只将一对减摇鳍安装在了船体两侧，具体建模模型如图1所示。

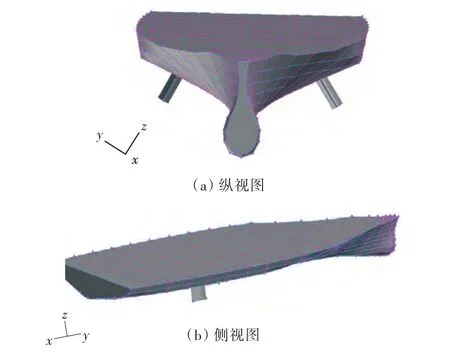
图1 GAMBIT建模Fig.1 GAMBIT modeling

依据减摇鳍的几何参数以及船体的船型型值表，利用FLUNET前处理软件GAMBIT建立数值模拟模型［4］。坐标系的选取为x指向下游，y指向右舷，z垂直向上，坐标原点设置在鳍轴的圆点处，计算域的建模如图2所示。整个计算域包括：

图2 计算域建模Fig.2 Computational domain modeling

1）上游边界：距船艏2倍船长；

2）下游边界：距船艉1倍船长；

3）侧面边界：距船体1/2倍船长；

4）船体壁面以及减摇鳍壁面。

计算域的边界条件包括：

1）进口边界条件，在计算域的进口处，给定速度大小和方向。

2）出口边界条件，使用压力出口条件，即给定静压。

3）壁面边界条件，在船体表面上满足无滑移条件。

4）对称面边界条件，在对称面上满足对称边界条件。

1.2 网格划分

在CFD计算中，网格的划分是十分关键的一步，会对FLUENT的仿真产生很大影响，而且在FLUENT仿真中，70%的精力要花在几何模型的建立以及网格的划分上［4］。由于带附体的舰船模型非常复杂，要对如此复杂的几何形状进行流场计算相当困难，因此网格生成的任务就显得异常重要。要想得到质量好的网格，首先需做好几何的建模工作，保证几何体上没有小的缝隙和碎面，这是将来网格生成成功与否的关键。对于如此复杂的几何形状，已不适合使用单块结构网格，多块网格生成方法在处理形状复杂物体的网格划分上具有相当的优越性。多块网格生成的第一步就是根据船舶结构的复杂性以及几何特点进行网络拓扑结构的建立，即将计算区域分成一定数量的子块，然后划分网格。这种网格划分方法为不同子块之间使用不同的网格分辨率提供了可能，同时还减少了网格划分所花费的精力。这种网格划分方法在研究船体与附体之间的相互影响上具有很大的潜力，因此，本文将采用多块网格生成方法［5-6］。

1.3 数值求解

在前处理软件GAMBIT中建立好几何模型并划分出质量好的网格后，就可以将模型导入FLUENT中进行数值计算了。在FLUENT中，设置的关键是要设置好压力与速度的耦合迭代。为了建立求解方程的有效算法，必须考虑一些特殊的情况，即连续性方程和压力没有直接联系，也即压力在连续性方程中不起作用。针对以上问题，目前已经出现了采用许多不同的解法来进行速度和压力的耦合求解，本文使用的是SIMPLE方法［7］，即求解压力耦合方程的半隐式方法，该算法是使用压力与速度之间的相互校正关系来强制质量守恒并获取压力场。另外一个重要的步骤就是湍流模型的选取。湍流模型是以雷诺平均运动方程和脉动运动方程为基础，依靠理论和经验的结合，引进一系列的模型假设而建立起来的一组描写湍流平均量的封闭方程组。最早的模型化思想是用涡粘性系数模拟雷诺应力，此后，在此基础上又逐渐建立了各种关于雷诺应力的模型假设，使雷诺应力方程得以封闭。FLUENT中提供了多种湍流模型，本文选用的是RNG k-ε湍流模型，其中k为湍动能，ε为耗散率。RNG k-ε模型与标准k-ε方程之间有相似的形式，其中湍流动能生成项的计算与标准k-ε模型完全相同。湍流粘性为

RNG k-ε湍流模型与标准k-ε模型的主要区别在于增加了以下项：

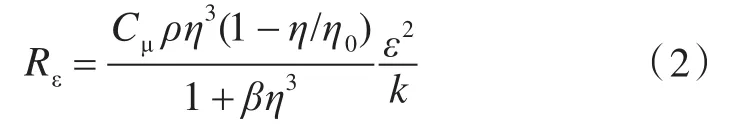
式中：η=Sk/ε；η0=4.38；β为热膨胀系数，β=0.012；Cμ为经验常数，Cμ=0.0845。模型常数 C1ε和C2ε由RNG理论可得：C1ε=1.42 ，C2ε=1.68；σk，σε为湍流普朗特数 σk=1.0，σε=1.3。由于使用的是三维动态仿真方法，所以必须利用FLUENT动网格技术，编写UDF函数设置鳍翼绕转轴摆动，并设置鳍翼为刚体运动，即摆动过程中鳍翼的外形没有变化。在中、高航速下，鳍翼绕鳍轴转动的角度的运动方式为正弦函数：

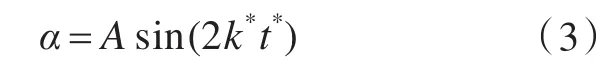
式中：A为鳍摆动的最大角度幅值，A=40°；k*为缩减频率，k*=，其中ω为角频率，ω=；t*=。仿真参数设置来流速度U=9.26 m/s，即为18kn航速转化而来；雷诺数

而在低航速的仿真中，由于航速低时流过鳍表面的水流速度小，无法产生足够大的升力，主要是靠驱动鳍快速挥摆而产生升力，因而鳍的运动方式与中、高航速不同。为此，在低航速的半个周期内，鳍角速度采用了匀加速、匀速、匀减速停顿的运动方式。除与前述动态所设置的UDF函数不同外，其余设置均相同。接着，设定收敛参数及欠松弛因子，显示残差图，并定义计算域中的变量监视图。设置升力、阻力及力矩的变量监视图，最后，取远场参数初始化整个流场，迭代计算并保存。

2 仿真模拟结果与分析

2.1 静态仿真分析

首先，通过FLUENT数值计算得到在高航速下的静态敞水条件下，减摇鳍与受船体约束减摇鳍的升力、阻力及力矩系数对比［8-9］，如图3所示。图中，线条1为受船体约束的减摇鳍，线条2为敞水条件下的减摇鳍。

由图3可以看出，受船体约束的减摇鳍的升力、阻力以及力矩均比敞水条件下的减摇鳍大。图4显示了减摇鳍在各个攻角下的受力云图和压力轮廓。由图可以看出，在0°～35°攻角间，减摇鳍的最大受力位置是不断变化的，且在同样的角度下，受船体约束的减摇鳍的受力更大。

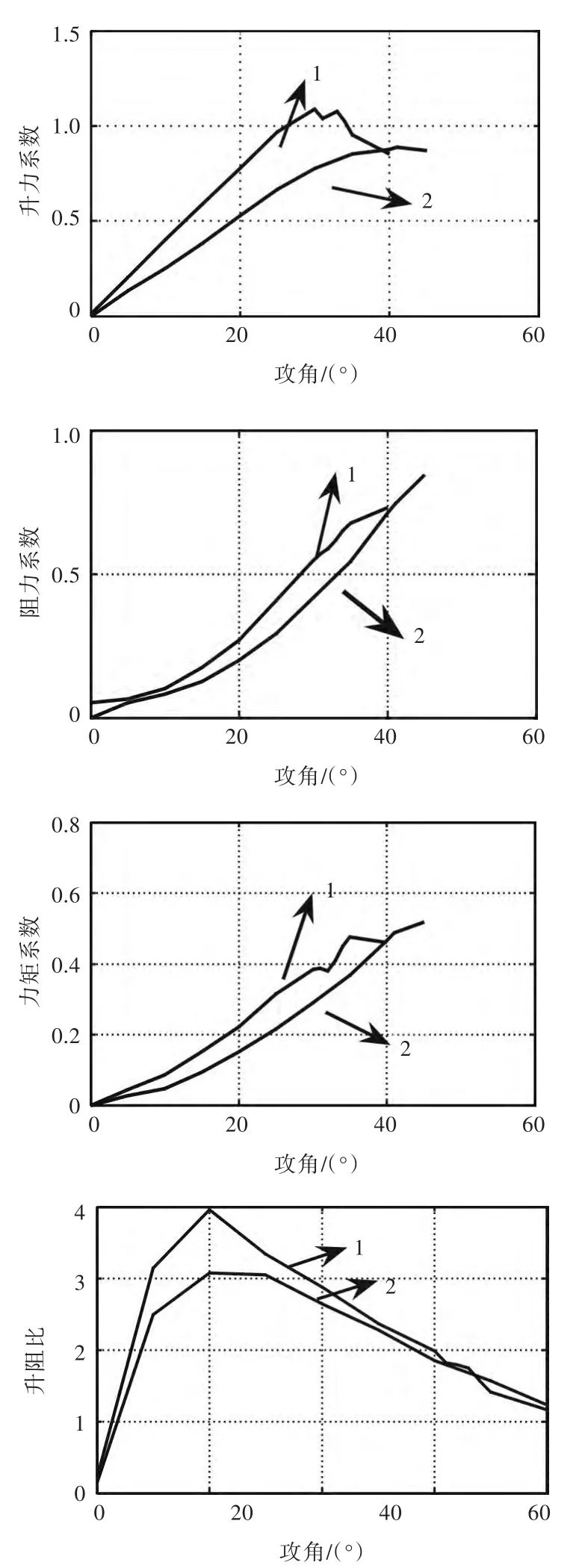
图3 受船体约束减摇鳍与敞水条件下减摇鳍的升力、阻力及力矩系数对比Fig.3 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin

图4 受船体约束减摇鳍（左）与敞水条件下减摇鳍（右）在各攻角下的受力云图Fig.4 The stress contours under different angles of attack between the fin added on the hull（left）and the isolated fin（right）

2.2 高航速动态仿真分析

若要充分分析减摇鳍与船体之间的相互影响，仅分析减摇鳍的静态水动力特性远远不够，因为减摇鳍无论是对船舶进行减摇还是操纵船体，在大部分情况下，减摇鳍都是运动的，因此对减摇鳍的动态仿真就显得尤为重要。为了得到较有说服力的试验结果，利用FLUENT进行数值计算，将减摇鳍的运动方式设置为传统的正弦运动方式［8］，在船舶航行速度为18 kn的情况下，对减摇鳍的正弦运动周期为4，6，8 s的情况进行了仿真，得到了高航速下动态敞水条件下的减摇鳍与受船体约束减摇鳍的升力、阻力及力矩系数对比，如图5～图7所示。图中，线条1为受船体约束的减摇鳍，线条2为敞水条件下的减摇鳍。

由图5～图7可以看出，两个完全相同的减摇鳍在同样的海况下，受船体约束减摇鳍的升力、阻力以及力矩系数均比敞水条件下的减摇鳍大。图8所示为仿真的横截面受力云图，从中可观察到敞水条件下减摇鳍与受船体约束减摇鳍运动时周围流场的受力云图。由图中可看出，在减摇鳍向上拍动的过程中，由于船舶的运动速度，以及运动的水流与鳍面的相互作用，在鳍上的压力比较大。另仔细观察受力云图不难发现，受船体约束的减摇鳍因船壁对水流的阻挡作用，必然会使鳍快速拍动时产生的漩涡与船壁发生挤压作用，从而使鳍拍动时产生更大的压力。

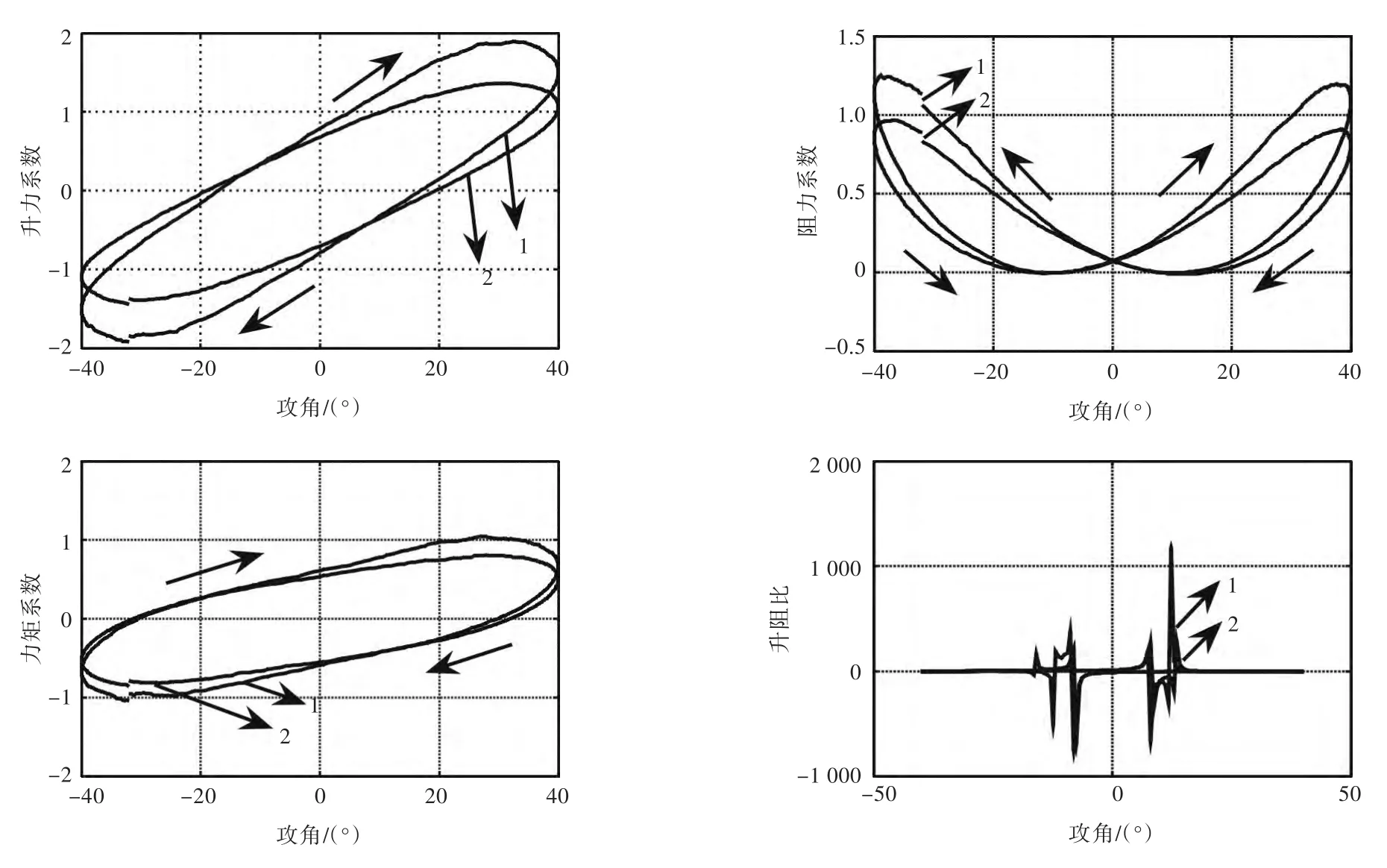
图5 受船体约束减摇鳍与敞水条件下减摇鳍在周期为4 s时的升力、阻力及力矩系数对比Fig.5 Comparisons of fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin at T=4 s

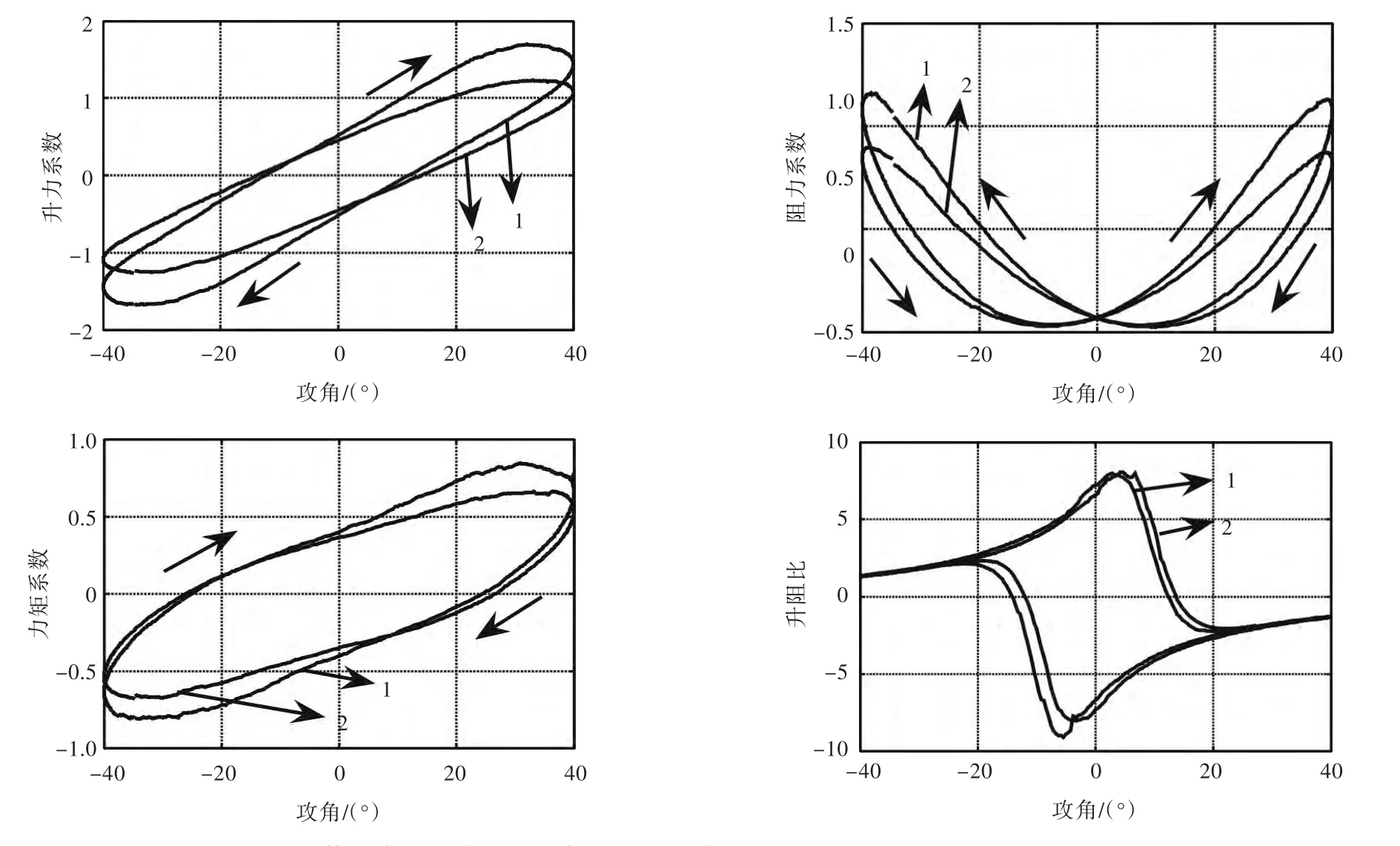
图6 受船体约束减摇鳍与敞水条件下减摇鳍在周期为6 s时的升力、阻力及力矩系数对比Fig.6 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin at T=6 s

图7 受船体约束减摇鳍与敞水条件下减摇鳍在周期为8 s时的升力、阻力及力矩系数对比Fig.7 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin T=8 s

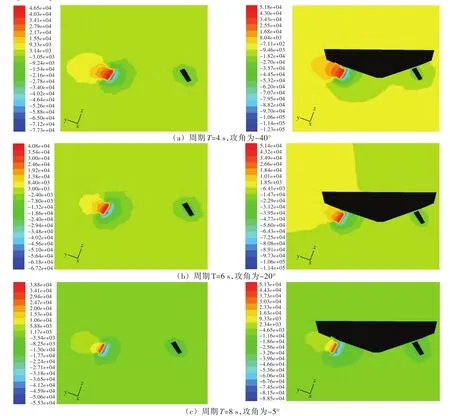
图8 敞水条件下减揺鳍（左）与受船体约束减揺鳍（右）的运动压力轮廓对比图Fig.8 The outline pressure figure between the isolated fin（left）andthe fin added on the hull（right）

综上所述，在高航速下，无论减摇鳍是在静止或是运动状态下，受船体约束减摇鳍的升力系数、阻力系数以及力矩系数均比敞水条件下减摇鳍的大。另外，由于带附体船体的复杂性，船体周围的流场也极其复杂，因此出现这种情况的原因也是多方面的。本文对这种情况的原因分析如下：

1）由于船体是一个在水中运动的壁面，所以不可避免地会在壁面附近产生边界层。所谓的边界层，就是大雷诺数流动问题中贴近物面的一个粘性薄层，即定常绕流中流体粘性只在贴近物面极薄的一层内主宰流体运动的薄层［10］。雷诺数Re表示Navier-Stokes方程中惯性力与粘性力的比值，大雷诺数流动就意味着粘性应力相对于惯性力很小，这时，可将粘性流体近似为理想流体。当水流从入口以均匀定常的高速绕流过减摇鳍时，流动的雷诺数很大，按照理想流体无粘流动，流体会在鳍面均匀地滑移过去。而实际上鳍面的流速为零，离开平板很小的距离后，流体速度开始迅速增大至均匀流动，由于减摇鳍的升力与水流速度有关，所以在一定程度上受船体约束减摇鳍在边界层的影响下升力会有所下降。而且当减摇鳍距离船艏越远，离船体越近时，这种边界层的效应对升力的影响也越大，会使鳍翼升力减小，流体机械效率降低，螺旋桨性能下降等，因此一般希望避免或尽量推迟分离的发生。但有时也可以利用分离，如小展弦比尖前缘机翼的前缘分离涡可以导致很强的涡升力［11］。而本文所使用的鳍翼就是小展弦比的尖前缘翼型，前缘分离涡的涡升力也许就是导致这种现象发生的原因。

2）船舶航行时，其附近的水受船体的影响会产生伴随在船体周围流动的水流，这种追随船体运动的水流即为伴流。由于伴流的存在，使得减摇鳍与其附近水流的相对速度与船速不同，在舷侧处，水流具有向后的速度，故为负伴流。由此而形成的伴流即称为形势伴流或势伴流。因流线离船身不远处即迅速分散，故在船体略远处其作用不甚显著，亦即离船体愈远，形势伴流的数值便愈小。因水具有粘性，故当船运动时，沿船体表面会形成界层，界层内的水质点具有向前的速度，而形成正伴流，通常称为摩擦伴流。摩擦伴流在紧靠船身处最大，由船身向外便急剧减小，离船体不远处即迅速消失。由于减摇鳍紧靠船体侧面，故既存在势伴流，又存在摩擦伴流，而由伴流的成因可知，伴流是一股极其复杂的水流，故伴流作用对上述情况的出现也有一定的作用。

2.3 零航速动态仿真分析

在航行状态下，由减摇鳍产生的稳定力矩大部分由鳍转到某一固定角度，由水流的作用产生升力来对抗海浪干扰力。而在船舶静止状态下，即零航速状态下，由于没有来流速度，因而零航速减摇鳍主要由鳍绕鳍轴在水平面内主动拍动来产生升力，而稳定力矩则仅由减摇鳍的快速拍动与静止的水之间的相互作用来产生［12］。这就意味着，零航速状态下减摇鳍的设计规律、操纵规律，以及液压系统和控制系统的设计规律与航行中减摇鳍的区别很大。零航速状态下减摇鳍的操纵规律与划桨的操纵规律类似［13］。

减摇鳍在静水中快速拍动所产生的用于稳定漂浮船舶所需的水动力的力矩来自流体的反应，而这些流体的反应则来自两方面的物理作用：

1）与减摇鳍的角加速度成比例的理想流体的惯性力，也称附加惯性力；

2）与减摇鳍的角速度的平方成比例的粘性流体阻力。

通常，航行中减摇鳍拍动的最大攻角即是最重要的性能参数，因此鳍的最大攻角是船舶航行时应慎重考虑的因素。但在船舶静止状态下，也即零航速状态下，鳍的摆动速率便取而代之成为所应考虑的重要参数。

为进一步研究敞水条件下减摇鳍与加在船体上减摇鳍的水动力特性的差异，本文再次利用FLUENT模拟了减摇鳍在低航速（如0 kn）状态下的受力情况。由于减摇鳍在零航速与高航速状况下的区别较大，故本文所采用减摇鳍的运动方式便不再是传统的正弦方式，而采用梯形的运动方式。这种升力产生机制的工作过程如下：当船舶从左横倾最大角开始向右舷方向运动时，鳍在伺服系统的驱动下，在恰当时刻开始产生一个抵抗海浪干扰力矩的稳定力矩，此力矩会维持一段时间直至快要达到右横倾最大角度。接着，船体会从右横倾最大角处向左舷运动，然后停顿一段时间，在这一过程中，减摇鳍控制器将再次控制伺服系统以驱动鳍面进行转动，进而产生抵抗海浪的稳定力矩来减小船体横摇。直至到达左横倾最大角度，并在最大攻角处再停留一段时间，至此，便完成了一个船舶横摇周期。通常，在半个周期内，鳍的运动可以分为加速起动、匀速运动、减速制动及停顿4个阶段。为此，本文利用FLUENT的UDF功能，用C语言对梯形运动方式进行设置。为充分研究，依然设置了3组试验，分别为周期T=4，6，8 s，并且在拍动过程中，其在加速、减速、匀速以及停顿部分的比例相同。周期T=4 s时的加速、匀速、减速以及停顿在半个周期内分别为0.2，0.5，0.3和1 s。为了对比不同周期下的不同情况，在周期T=6 s时，设置加速、匀速、减速以及停顿在半个周期内分别为0.3，0.75，0.45和 1.5 s，在周期T=8 s时，设置加速、匀速、减速以及停顿在半个周期内分别为0.4，1，0.6和2 s，由此可得梯形运动方式拍击所产生的升力、阻力与力矩对比图，如图9～图11所示。图中，线条1为船体约束的减摇鳍，线条2为敞水条件下的减摇鳍。

图9 受船体约束的减摇鳍与敞水条件下减摇鳍在周期为4 s时产生的升力、阻力及力矩对比Fig.9 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin at T=4 s

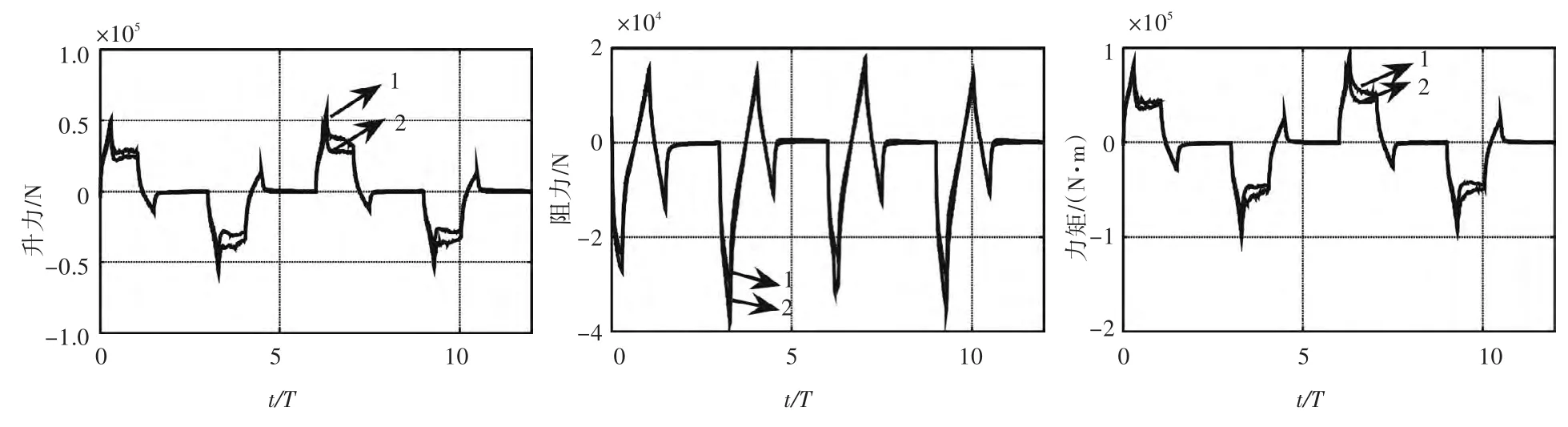
图10 受船体约束的减摇鳍与敞水条件下减摇鳍在周期为6 s时产生的升力、阻力及力矩对比Fig.10 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin at T=6 s

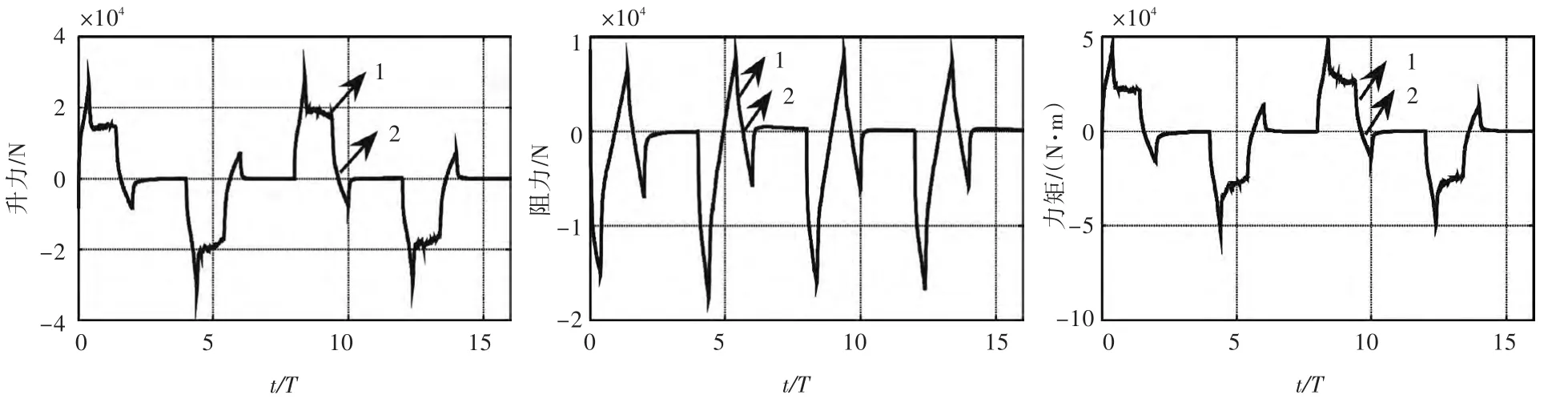
图11 受船体约束的减摇鳍与敞水条件下减摇鳍在周期为8 s时产生的升力、阻力及力矩对比Fig.11 Comparisons of the fins'lift，resistance and moment coefficients between the fin added on the hull and the isolated fin at T=8 s

对比图9～图11不难发现，在零航速状态下，以梯形运动方式拍动的减摇鳍虽然周期越短产生的升力越大，减摇效果也越好，但其阻力以及力矩也相应地有大幅的增加，由此，相应的能量消耗必然也大。考虑到经济效益，不能一味追求减摇效果，因此应选择适当的拍动周期。另外还发现，在零航速状态下，受船体约束的减摇鳍所产生的升力和力矩均比敞水条件下的减摇鳍高，而阻力却基本不变，可见在船舶航行过程中，水流速度是船舶航行阻力的一个重要因素。此外，对比3个周期的图形可以发现，在周期T=4，6 s情况下，受船体约束的减摇鳍产生的升力、阻力和力矩均比敞水条件下减摇鳍的大，而在周期T=8 s时，两者基本不变。

为了更形象地显示仿真结果，图12和图13显示了敞水条件下减揺鳍与加在船体上减揺鳍的横剖面和纵剖面的压力轮廓云图，图14显示了敞水条件下减揺鳍与加在船体上减揺鳍的纵剖面的速度轮廓云图，图15为敞水条件下减揺鳍与加在船体上减揺鳍的三维立体流线图。

从图12的横剖云图和图13的纵剖云图（左图为敞水条件下的减揺鳍）可以看出，在零航速状态下，由于没有水流流速的作用，而仅仅是减揺鳍在水中快速拍动，当鳍绕鳍轴在水中快速拍动时，鳍会排开周围的流体迫使流体向四周运动，而受船体约束的减揺鳍由于有了船体的阻挡作用必然会受到一定的阻力，所以从压力云图中不难发现，受船体约束的减揺鳍拍动时所承受的压力要比敞水条件下的减揺鳍大得多。

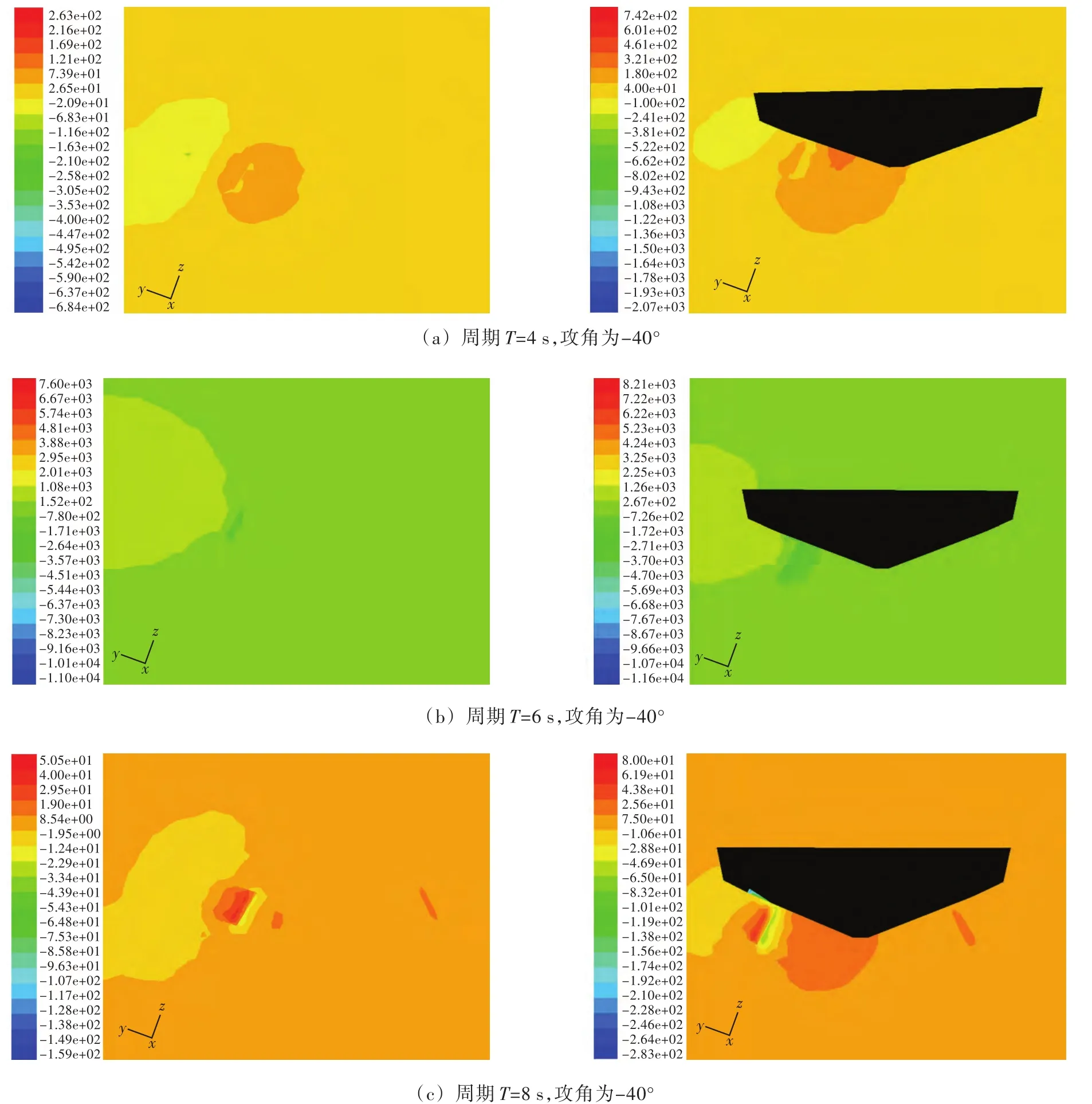
图12 敞水条件下减揺鳍（左）与受船体约束减揺鳍（右）的运动压力轮廓对比图（横剖面）Fig.12 Comparisons of outline pressure figure（transverse section）between the isolated fin（left）and the fin added on the hull（right）

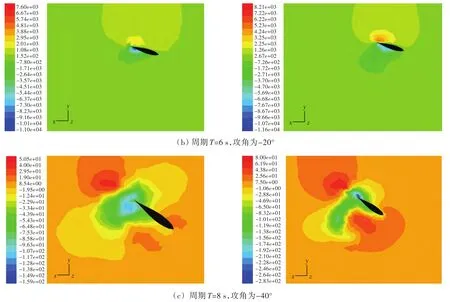
图13 敞水条件下减揺鳍（左）与受船体约束减揺鳍（右）的运动压力轮廓对比图（纵剖面）Fig.13 Comparisons of outline pressure figure（longitudinal section）between the isolated fin（left）and the fin add on the hull（right）

从图14的速度轮廓对比云图（左图为敞水条件下的减揺鳍）中不难发现，在零航速情况下，减揺鳍拍动时尾缘涡对诱导速度的作用要比前缘涡大，并且受船体约束的减揺鳍在尾缘由尾缘涡所产生的速度要比敞水条件下的减揺鳍大得多。

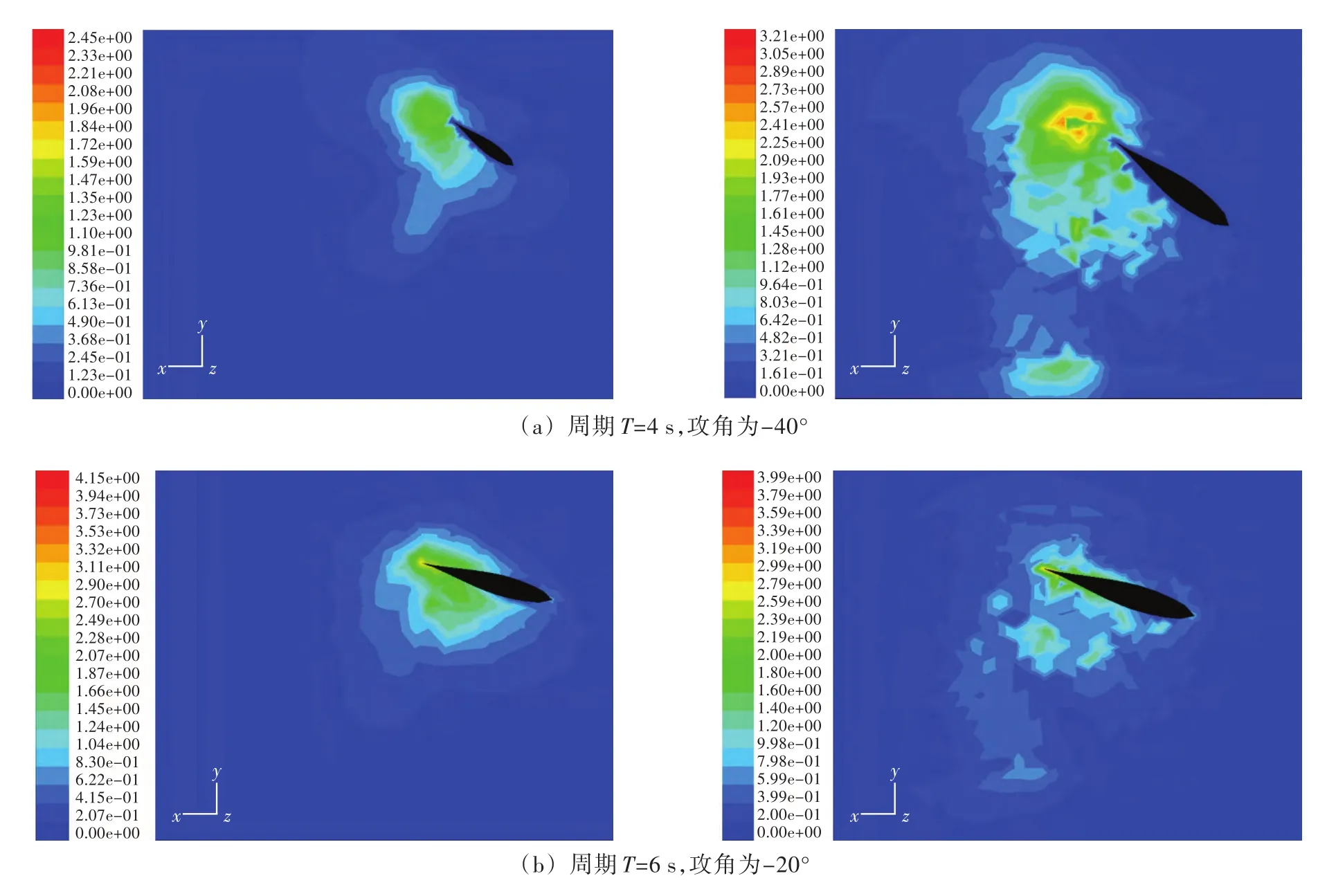
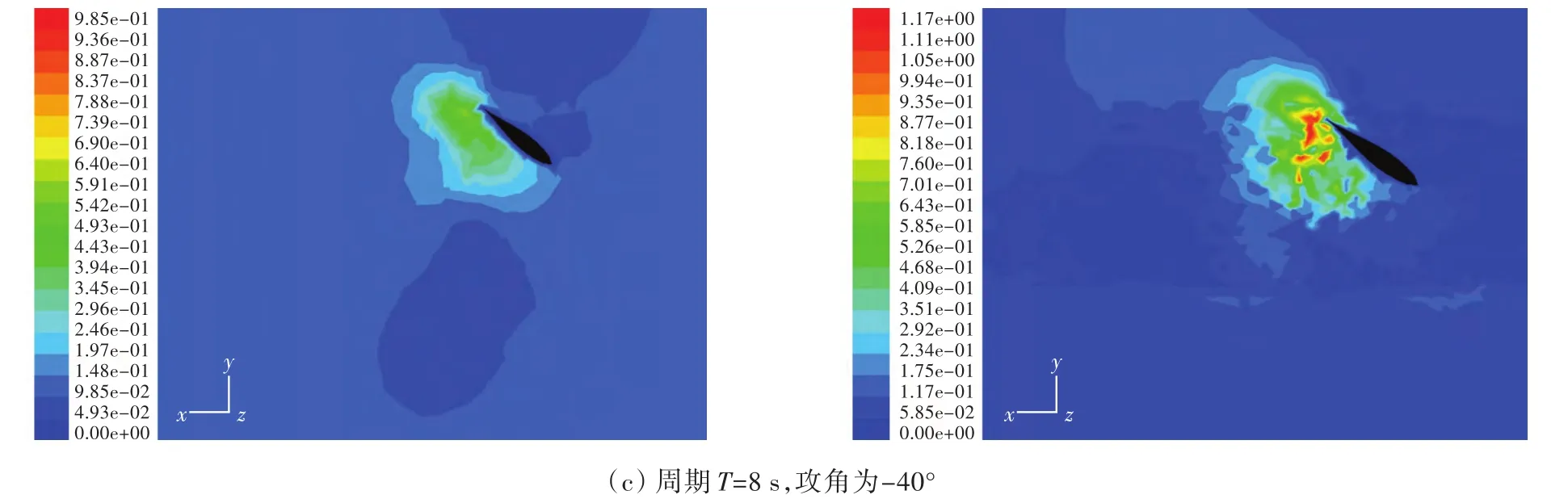
图14 敞水条件下减揺鳍（左）与受船体约束减揺鳍（右）的速度轮廓云图Fig.14 The speed profile figure between the isolated fin（left）and the fin added on the hull（right）

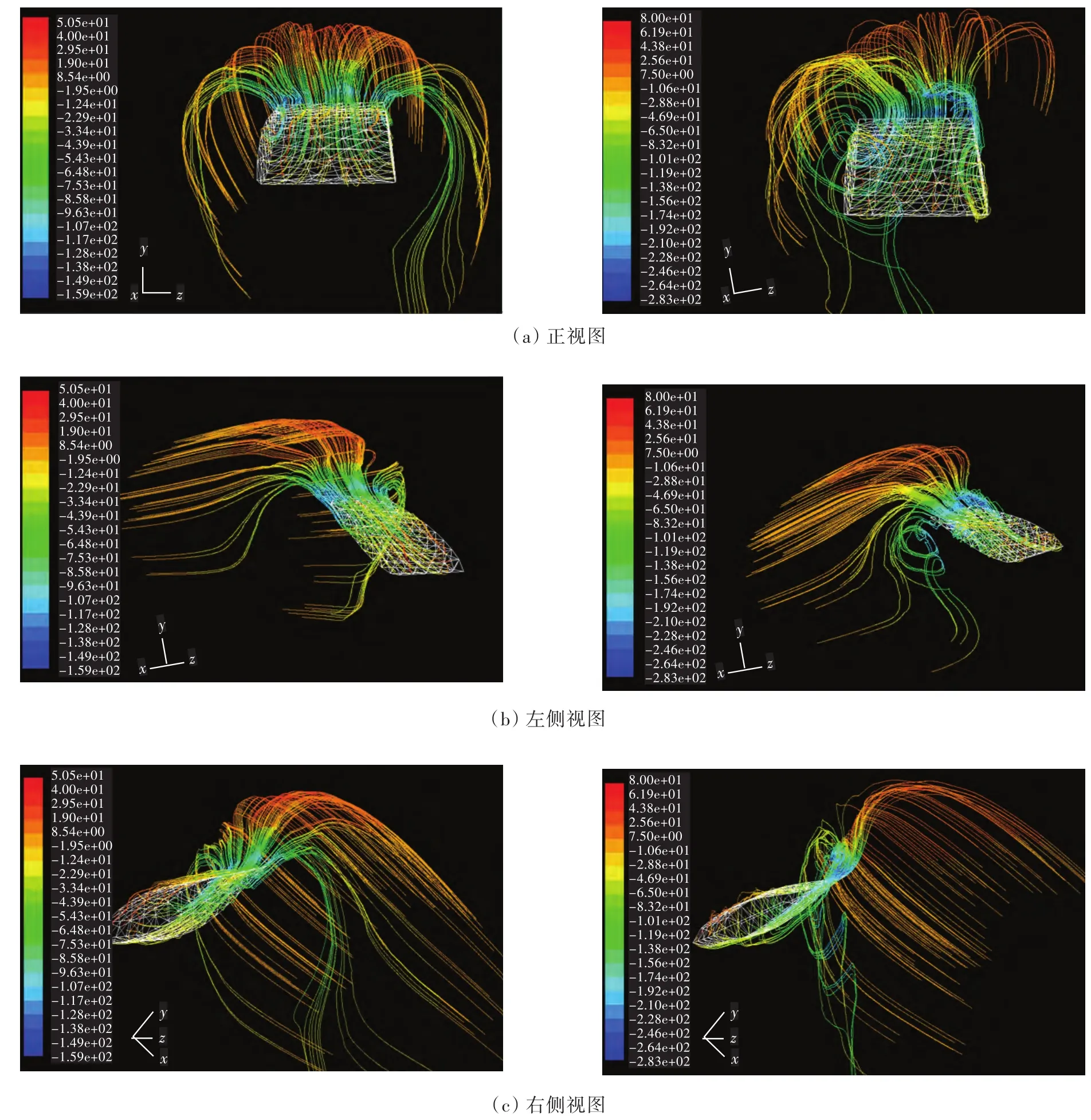
图15 敞水条件下减揺鳍（左）与受船体约束减揺鳍（右）的水流流线图Fig.15 The flow chart between the isolated fin（left）and the fin added on the hull（right）

图15所示的流线云图是周期T=8 s，当拍动至8 s时减揺鳍周围的水流流线图。由图中不难发现，在零航速状况下，受船体约束的减揺鳍由于船体的壁面效应，当减揺鳍向上拍动时，周围流体会向船体产生挤压，水流会由于船壁的阻挡作用而在尾缘产生漩涡，鳍面在非定常的流体中转动时旋涡的影响不容忽略［14］。前缘涡和尾缘涡将分别在鳍面形成诱导速度，使鳍面两侧产生压力差，这种压力差会使升力得到增加，即敞水条件下的减揺鳍相对来说升力更小的原因所在。

为了表示它们的水动力特性差异，综合以上动态仿真结果，表1给出了不同航速下动态仿真情况的数值表。

由表1可知：

1）在18 kn航速下，虽然周期越小，升力、阻力以及力矩越大，但无论周期是4，6 s还是8 s，受船体约束减摇鳍的升力均比敞水条件下减摇鳍的约大30%，阻力和力矩的增加也约为30%。

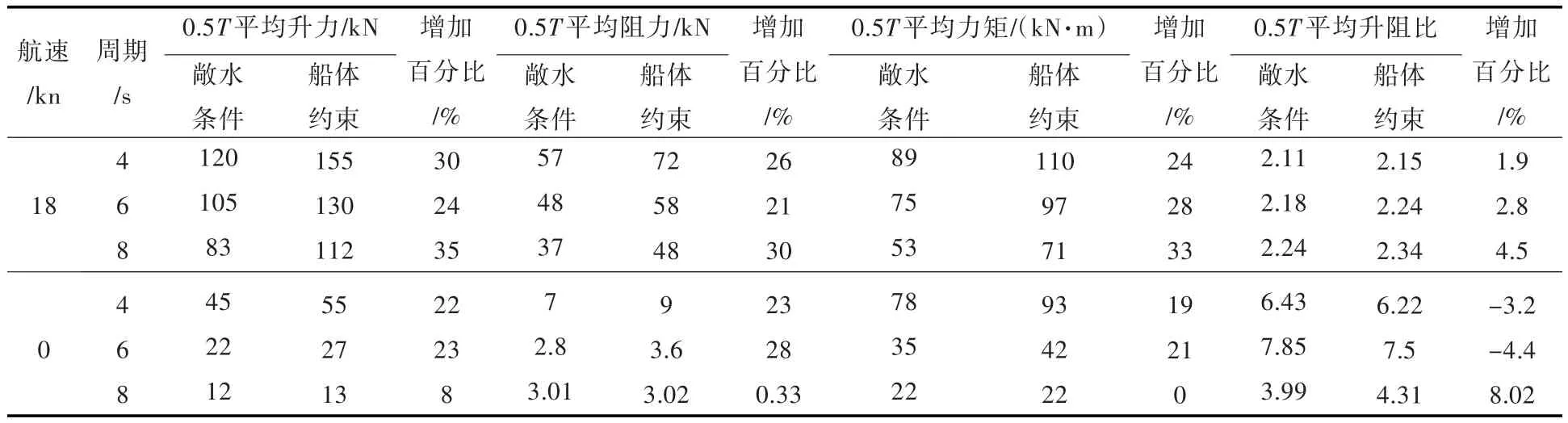
表1 动态仿真结果Tab.1 Dynamic simulation results

2）在0 kn航速下，同样也是周期越小，升力、阻力以及力矩越大。在周期为4，6 s时，受船体约束减摇鳍的升力、阻力以及力矩比敞水条件下减摇鳍的约增加了20%，但在周期为8 s时，无论是升力、阻力还是力矩，都基本无变化。

3）可以发现，在零航速状态下阻力均得到了大幅减少，其约为升力的15%，而在中、高航速状态下，阻力则约为升力的50%，但在零航速状态下驱动减揺鳍的力矩却比中、高航速状态下在产生同等升力的情况下大得多，这也就意味着在零航速状态下减揺鳍主动拍击的方式需要更多的能量。

4）可以发现在18 kn航速下，无论周期为4，6或是8 s，受船体约束减揺鳍的升阻比均比敞水条件下的大，而且周期越大增大的幅度越大。但在0 kn航速情况下，周期为4，6 s时受船体约束减揺鳍的升阻比比敞水条件下的要小，只有在8 s周期情况下受船体约束减揺鳍的升阻比要比敞水条件下的大。

综上所述，无论是中、高航速还是低航速，与敞水条件下的减摇鳍相比，受船体约束的减摇鳍有更加理想的减摇效果，说明减摇鳍与船体有很好的适配性。

3 结 论

本文应用FLUENT软件对受船体约束减摇鳍和敞水条件下减摇鳍的静态水动力特性与动态水动力特性进行了数值模拟，得出了它们在静态时的升力、阻力以及力矩系数的对比图和在动态时航速分别为18 kn和0 kn下升力、阻力和力矩的对比图，并对产生这种结果的原因进行了分析，通过分析以上数值模拟结果，得出以下结论：

1）由于球鼻艏对船速的提速作用，边界层分离的前缘分离涡的强涡升力，或者是船体周围复杂水流运动所产生的极其复杂的伴流，使得受船体约束的减摇鳍的升力、阻力以及转鳍力矩均有大幅提高，但相对来说是利大于弊，减摇效果可以得到大幅提升。

2）受船体约束减摇鳍的升力、阻力以及力矩比敞水条件下减摇鳍的大，因此减揺鳍与船体无论是在中、高航速还是低航速均有较好的适配性。

［1］KARTIKEYA M.Cavitating flow over oscillating hydrofoils and hydrofoils-based ship stabilization system［D］.Ohio：University of Cincinnati，2008.

［2］GAILLARDE G.Pitch reduction in transit by using stabiliser fins［C］//The Model Yacht Conference，Royal Institution of Naval Architects，2008.

［3］READ D A，HOVER F S，TRIANTAFYLLOU M S.Forces on oscillating foils for propulsion and maneuvering［J］.Journal of Fluids and Structure，2003，17（1）：163-183.

［4］韩占忠.FLUENT——流体工程仿真计算实例与分析［M］.北京：北京理工大学出版社，2009.

［5］綦志刚.船舶零航速减摇鳍升力机理及系统模型研究［D］.哈尔滨：哈尔滨工程大学，2008.

［6］陈材侃，刘华.解三维水翼绕流的下潜涡环栅格法［J］.船舶力学，2005，9（2）：41-45.CHEN Caikan，LIU Hua.A submerged vortex lattice method for calculation of the flow around a three-dimension hydrofoil［J］.Journal of Ship Mechanics，2005，9（2）：41-45.

［7］江帆，黄鹏.FLUENT高级应用与实例分析［M］.北京：清华大学出版社，2008.

［8］金鸿章，姚绪梁.船舶控制原理［M］.哈尔滨：哈尔滨工程大学出版社，2001.

［9］DALLINGA R P.Roll stabilisation of motor yatchs：use of fin stabilizers in anchored conditions［J］.Project，1999，99：5.

［10］张亮，李云波.流体力学［M］.哈尔滨：哈尔滨工程大学出版社，2001.

［11］TRIANTAFYLLOU M S，TECHET A H，HOVER F S.Review of experimental working in biomimetic foils［J］.IEEE Journal of Oceanic Engineering，2004，29（3）：585-594.

［12］金鸿章，王龙金.零航速下变鳍型减摇鳍升力模型研究［J］.中国造船，2010，51（2）：1-9.JIN Hongzhang，WANGLongjin.Research on lift model of transmutative finstabilizer at zero speed［J］.Shipbuilding of China，2010，51（2）：1-9.

［13］张晓飞.船舶零航速减摇鳍建模及控制策略研究［D］.哈尔滨：哈尔滨工程大学，2008.

［14］代钦，赵莉莉.自由表面对小攻角翼型流动分离特性的影响［J］.水动力学研究与进展：A辑，2009，24（3）：259-265.DAI Qin，ZHAO Lili.Influence of free surface to the flow separation of an airfoilwith a small angleof attack［J］.Journal of Hydrodynamics（Ser.A），2009，24（3）：259-265.