规则波六自由度回转运动预报
2014-11-12徐静顾解忡马宁
徐静,顾解忡 ,马宁
1 中国舰船研究设计中心,湖北武汉 430064
2 上海交通大学海洋工程国家重点实验室,上海 200240
0 引言
在设计阶段,研究船舶在静水中的操纵运动旨在为评估船舶的操纵性能提供可靠依据。然而,船舶在海上航行时总会遇到波浪,且其影响往往不可忽略。此时,船体运动除水平面内的操纵运动外,还伴有铅垂面内的横摇、纵摇和垂荡运动,波浪作用会导致船舶操纵性能变差,推进效率降低,带来耐波性问题,甚至对船舶的航行安全产生重大影响。
有关船舶在波浪中的操纵运动的研究,最早Hirano等[1]提出了一种在三自由度 MMG(ship manoeuvring mathematical model group)模型中直接加入二阶波浪漂移力的建模方法,并据此计算了规则波中的回转运动轨迹,其中二阶波浪漂移力由模型试验获得。随着数值模拟方法的发展,研究者开始意识到摇荡运动和一阶波浪力对船舶操纵性的影响。Kijima等[2]考虑了一阶波浪力和横摇运动对船舶操纵性的影响,建立了四自由度运动模型,并分析了不同波浪条件对船舶回转运动的影响。安川宏纪[3]则进一步提出了波浪中操纵—耐波六自由度全耦合运动模型,计算了一艘集装箱船在不规则波下的回转运动,并与水槽试验结果进行了对比,虽然和前人相比有了很大的改进,但该模型未考虑垂荡和纵摇对船舶操纵运动的影响。Skejic等[4]也考虑了船舶操纵与耐波运动的耦合,建立了六自由度的统一模型对船舶操纵运动进行时域数值模拟,模拟结果通过与静水中的自航模试验结果进行对比,验证了其准确性。其中一阶波浪力采用STF切片法计算,二阶波浪漂移力采用了3种势流理论方法计算,但其波浪力的计算还只局限于频域,计算结果也只强调了船舶水平面的运动情况,没有给出摇荡运动时历。
本文提出了该模型综合考虑船体兴波作用、记忆效应以及二阶波浪漂移力的影响的六自由度操纵运动数学模型,并利用该模型对一艘S175集装箱船在规则波中的回转运动进行了时域数值模拟,在验证模型适用性的基础上讨论了操纵—耐波运动耦合作用的影响。
1 六自由度操纵运动数学模型
1.1 坐标系和船体运动方程
如图1所示,取空间固定坐标系O0-X0Y0Z0,使O0-X0Y0与静水面重合,O0Z0轴则垂直于静水面,取向下为正;取随体坐标系G-xbybzb,Gxb轴与基线平行,指向船艏为正,Gyb轴则垂直于船舯剖面,以指向右舷为正。
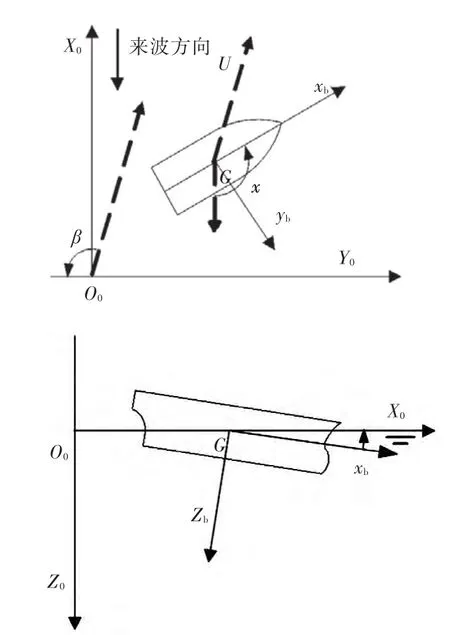
图1 坐标系Fig.1 Coordinate system
船舶在O0-X0Y0Z0中的重心坐标(x0,y0,z0)和船体姿态(ϕ,θ,ψ),与在 G-xbybzb中重心处的线速度(u,v,w )及角速度 (p,q,r) 之间有如下变换关系:

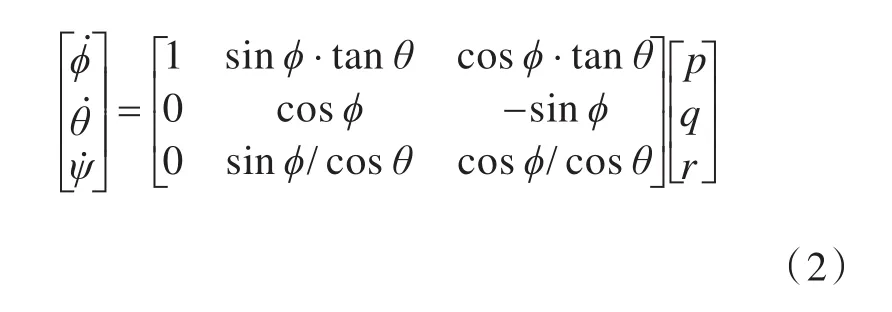
在G-xbybzb中,六自由度操纵运动方程可表示为式(3)形式:
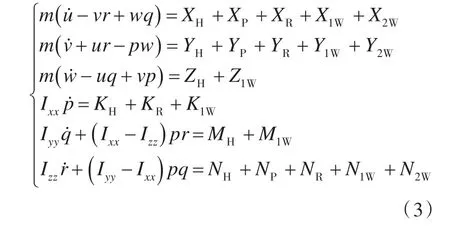
式中:m为船体质量;Ixx,Iyy,Izz分别为绕x轴,y轴和 z轴的惯性矩;下标H,P,R,1W,2W 分别表示船体力、螺旋桨力、舵力、一阶波浪力及二阶波浪漂移力;X,Y,Z为作用于重心处合力的3个分量;K,M,N为绕重心合力矩的3个分量。
1.2 船体力
作用在船体上的作用力可以分为惯性力和粘性力两类,FH=FHI+FHV。
所谓惯性类流体动力及力矩,即船舶在理想流体中作非定常运动时所受到的水动力,其大小与船体运动的加速度成比例,方向与加速度方向相反,其比例常数也称为附加质量(惯性矩)系数,用Ajk表示。考虑到船体的左右对称性并忽略量级较小的量,惯性类流体动力可表示为
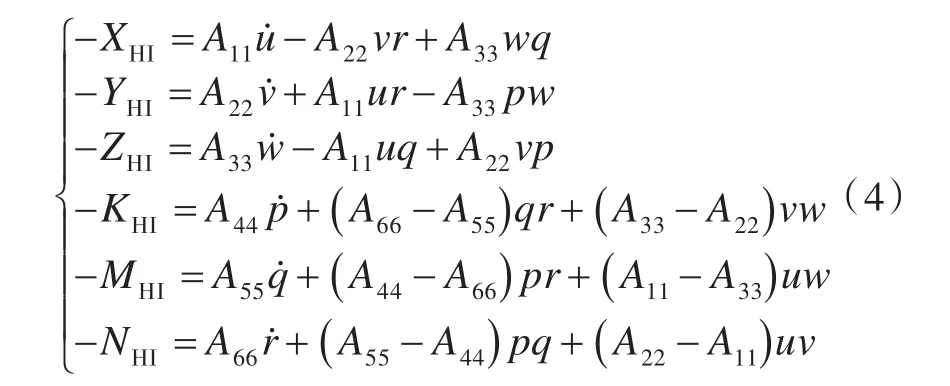
粘性类流体动力及力矩可近似为

式中的系数可采用经验公式估算。其中:zH,xc分别为船体动力YHV作用中心对xb轴和zb轴的力臂;Xuuu2为纵向阻力,包含摩擦阻力和剩余阻力,摩擦阻力系数可以采用ITTC-1957公式计算,剩余阻力系数则可参考泰勒图谱;Xvv,Xvr,Xrr采用松本方法[5]计算;Yv,Yr,Nv,Nr采用 Inoue等[6]的近似公式计算;而Yvv,Yrr,Yvvr,Yvrr,Nvv,Nrr,Nvvr,Nvrr则采用周昭明等[7]根据井上图谱得到的回归公式计算;Kp=,其中μ=0.0384,为横摇阻尼系数,根据自由横摇试验结果确定,GM 为横稳性高;MHV,NHV中的流体动力采用Tasai[8]提出的经验公式计算。
1.3 桨 力
桨力项用式(6)表示:
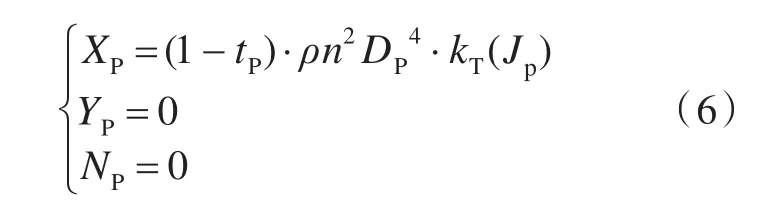
式中:YP=0,NP=0,这是因为常规螺旋桨产生的横向力和船舶转艏力矩通常都很小,可以通过修正舵力和舵力矩加以考虑;n为螺旋桨转速;DP为螺旋桨直径;tP为桨推力减额系数,采用汉克歇尔公式[9]估算,对于单桨标准型商船(方形系数Cb=0.54~0.84),取 tP=0.50CP-0.12,CP为棱形系数。

1.4 舵 力
舵力项用下式表示:
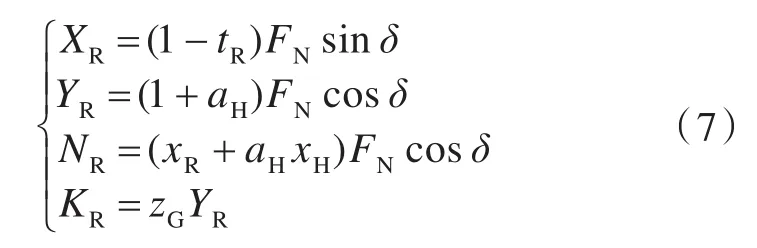
式中:tR为舵阻力减额系数,有1-tR=0.7382-0.0539Cb+0.1755;aH为操舵诱导的船体横向力的修正因子,aH=0.6784-1.3374Cb+1.8891;xH为操舵诱导的船体横向力作用中心至船舶重心的距离,xH=-L(0.4+0.1Cb);δ为舵角,取决于操舵指令;zG为舵力作用中心对xb轴的力臂。
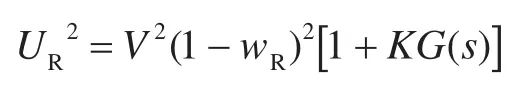
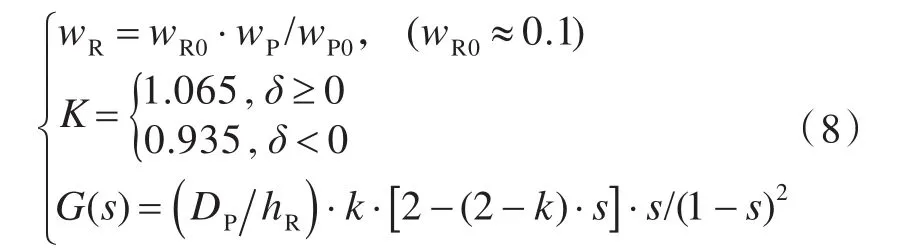
式中:wR为舵伴流分数;k为增速系数;s为滑脱比。
1.5 波浪力
根据无限水深线性势流理论,本文计入时域一阶波浪力及二阶波浪漂移力并建立了数学模型。其中,一阶波浪力可分为入射波力、绕射波力及辐射波力。本文建立的网格模型如图2所示,采用三维面元法软件计算出了零航速下ω=0.1~12 rad,浪向角 χ=0°~350°范围内的运动和波浪力响应数据。

图2 S175网格模型Fig.2 S175 mesh model
根据需要,也可简单采用Daidola等[10]的经验公式估算二阶波浪漂移力。
一阶波浪力是遭遇频率的函数,利用Cummins[11]的脉冲响应函数,辐射波力和入射、绕射波力分别为:
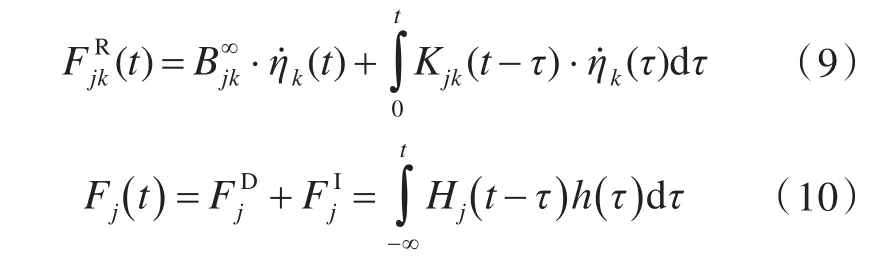
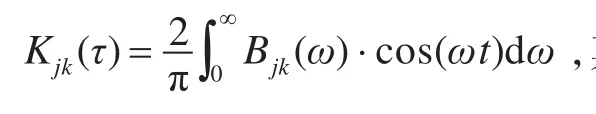
在船模运动过程中,遭遇频率会不断发生变化,遭遇圆频率可表达为
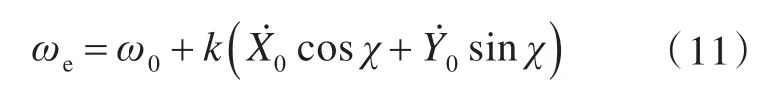
式中:ω0为入射波圆频率;k为波数;χ为浪向角。
2 船舶回转运动数值模拟
2.1 计算对象
本文的研究对象为S175集装箱船,自航模试验[12]在某大学的风浪流水池实施,船模缩尺比为57.686。该船的主要参数如表1~表3所示。
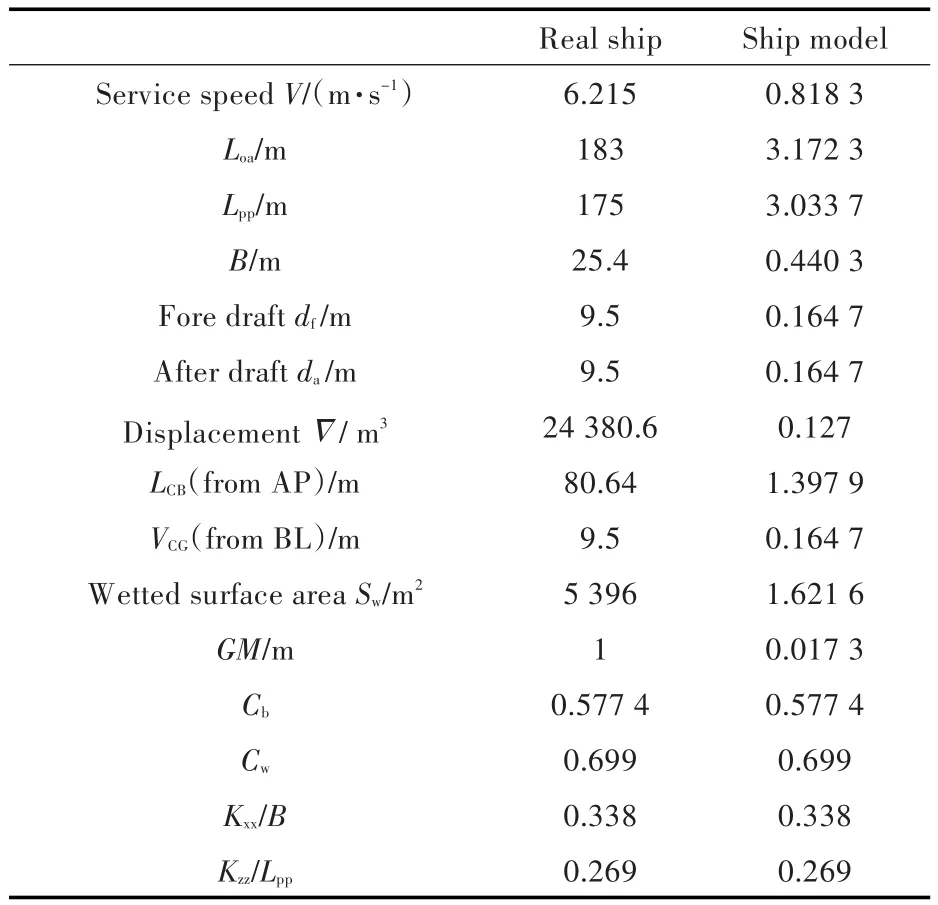
表1 S175船主要参数Tab.1 Main parameters of S175

表2 S175船螺旋桨的主要参数Tab.2 Main parameters of S175 propeller
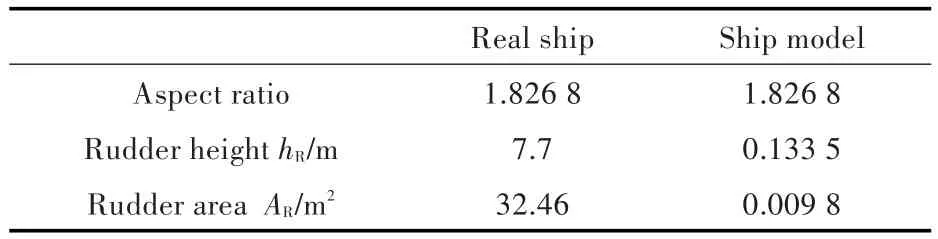
表3 S175船舵的主要参数Tab.3 Main parameters of S175 rudder
2.2 静水回转运动数值模拟
应用提出的数学模型,在不考虑波浪力的情况下对S175集装箱船进行回转运动的模拟计算,并与自航模试验结果进行了对比。图3所示为舵角±35°时的回转运动轨迹。从中可看出,模拟与试验结果大致吻合,说明静水中的操纵运动数学模型是合理的。
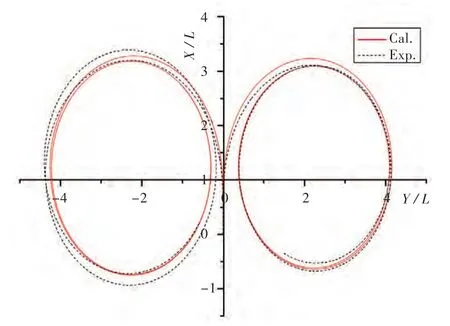
图3 静水回转运动轨迹模拟和试验对比图Fig.3 Comparison of turning circle trajectory between simulation and test in still water
2.3 规则波回转运动数值模拟
应用提出的数学模型,以迎浪、λ/L=1.4及波幅13.5 mm工况为例来模拟左舵35°时的回转运动情况。其中,初始航速(0.72m s)和波幅均依据试验记录设置。
图4所示为计算工况(迎浪规则波)下该集装箱船的回转运动轨迹。从中可看出,试验回转直径(4Lpp)与模拟回转直径(3.85Lpp)基本一致,回转直径的计算误差约为4%。回转运动漂移方向一致,均在回转经过240°方向处发生向X负方向和Y正方向的漂移。
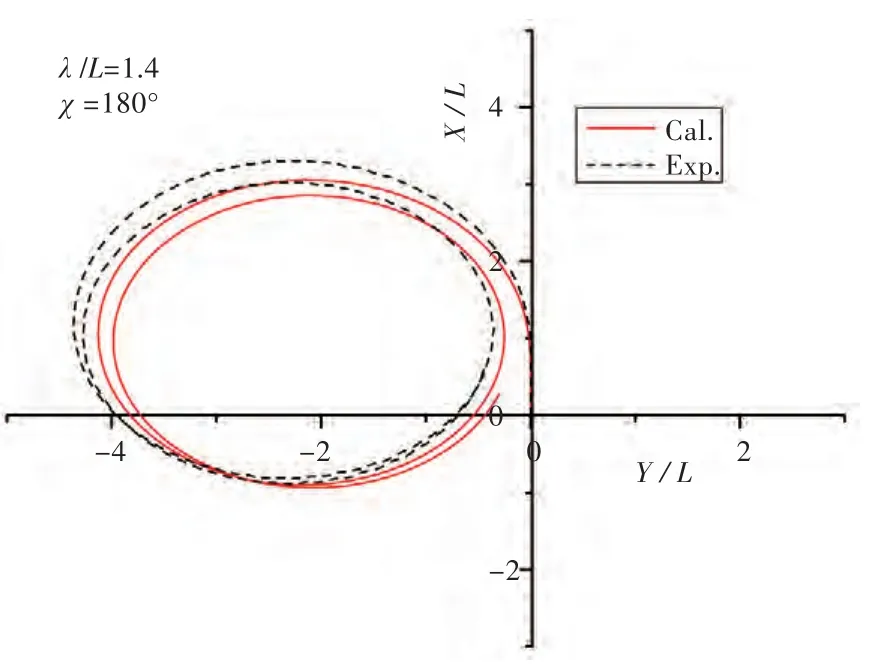
图4 规则波回转运动轨迹模拟和试验对比图Fig.4 Comparison of turning circle trajectory between simulation and test in regular wave
图5所示为规则波下该集装箱船的回转摇荡结果。
对于图5(a)所示的回转横摇时历曲线,横摇角的最大幅值为11°,其计算结果和试验结果相比大10%,但总体变化趋势一致。浪向角约为270°时的横摇幅值比浪向角为90°时的略小,究其原因,可能是因初稳性高和相对相位发生了改变,也有可能是受到了水池端部反射波的影响。从迎浪到横浪的变化过程中有10 s的小幅振荡,这是由船模运动的初始横倾造成的。
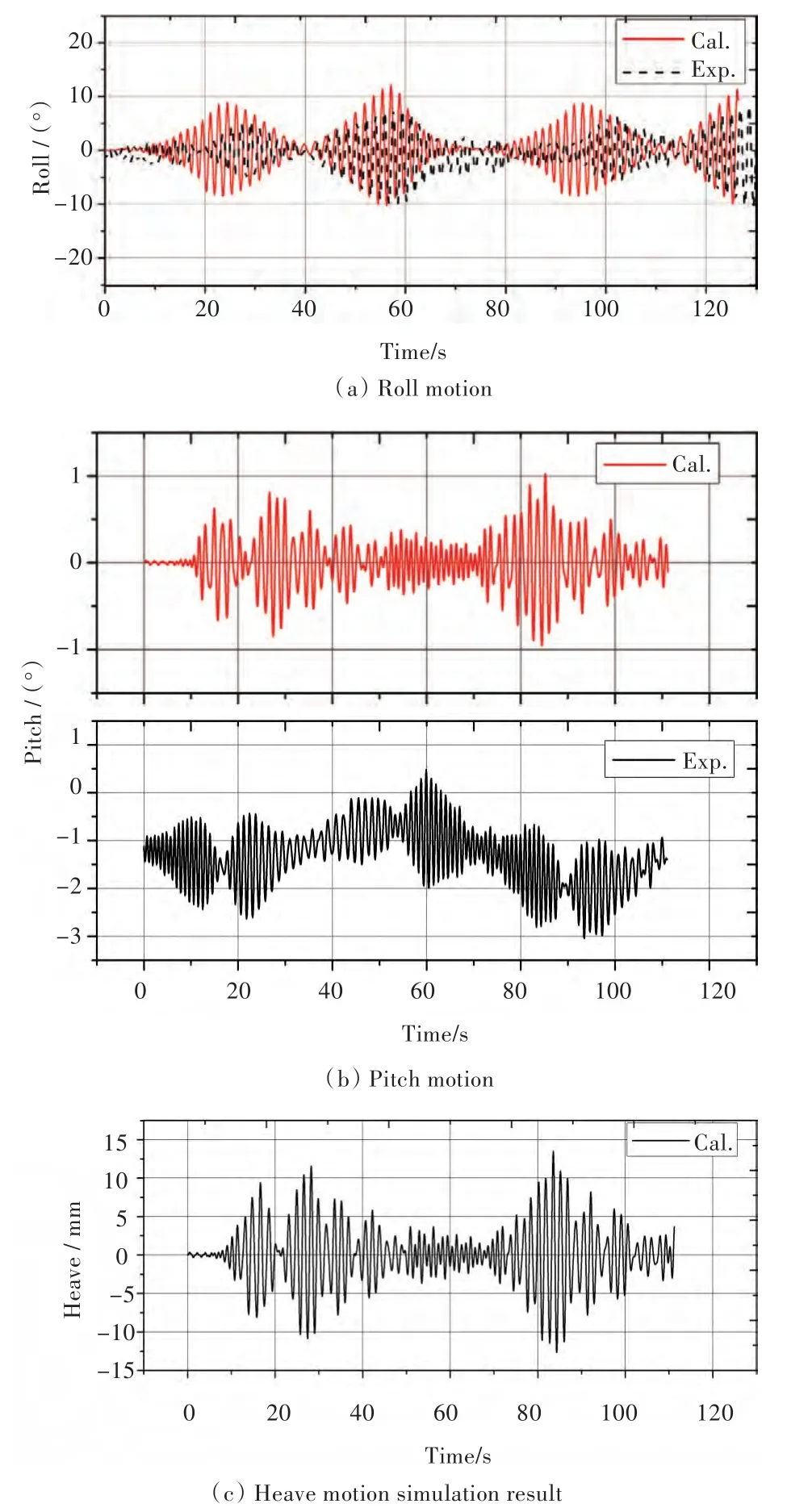
图5 回转摇荡运动模拟和试验结果对比图Fig.5 Comparison of turning circle oscillation motion between simulation and test results
对于图5(b)所示的回转纵摇时历曲线,纵摇角的最大幅值约为1.2°,试验记录的纵摇角最大幅值为1.1°,两者基本一致。在变化趋势方面,两者的振荡周期一致,试验结果为纵摇和垂荡的线性叠加时历,显示的是长周期的振荡,而模拟结果则只考虑了纵摇摇荡运动情况,故显示的是围绕0点的振荡运动。对于图5(c)所示的回转垂荡时历曲线,垂荡最大幅值约为10 mm,与试验情况相符。
纵摇和垂荡运动的幅值较小,对其他自由度的计算结果影响不大,故此处的计算精度已能满足总体精度需求。
图6给出了回转运动过程中重心处的瞬时波高时历、速度时历和遭遇波频时历。
综上所述,规则波中的六自由度操纵运动数学模型也是合理的。
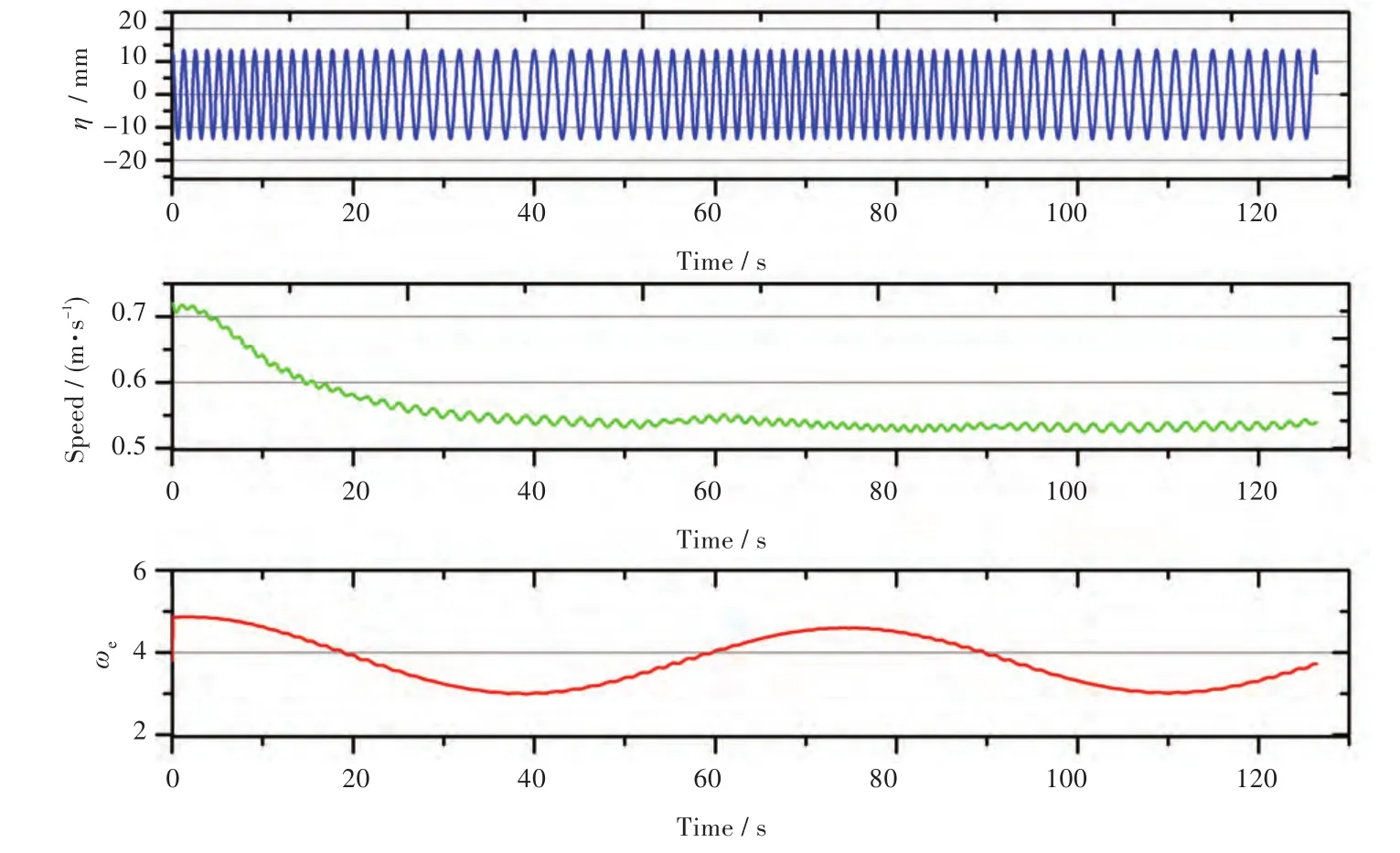
图6 回转运动模拟结果Fig.6 Turning circle simulation results
2.4 操纵—耐波耦合作用分析
应用提出的数学模型,讨论操纵—耐波耦合作用的影响。提出分别以六自由度的数学模型和三自由度的数学模型(基于MMG模型,考虑时域一阶波浪力和二阶波浪漂移力)讨论不同波浪条件下摇荡运动对操纵运动的影响,以分析考虑回转漂移和不考虑回转漂移的波浪条件下水平面运动对摇荡运动的影响,结果如下。
表4给出了工况情况,其中浪向角180°代表迎浪,T1代表高频波浪,T7代表低频波浪。
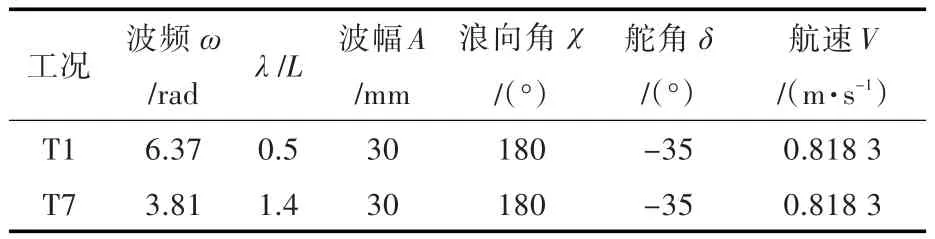
表4 工况表Tab.4 Case sheet
2.4.1 摇荡运动对操纵运动的影响
摇荡运动对操纵运动的影响如图7和图8所示。
由图7可看出,在高频波浪条件(T1)下,三自由度模型和六自由度模型模拟的回转轨迹一致,回转速降时历也基本吻合,差异在1%以内。
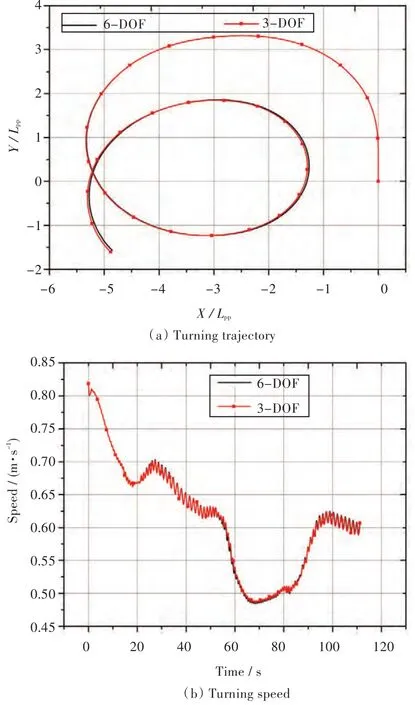
图7 T1工况下三自由度和六自由度模拟结果对比Fig.7 Comparisons of 3-DOF&6-DOF turning circle simulation results in case T1
由图8可看出,在低频波浪条件(T7)下,三自由度模型和六自由度模型模拟的回转轨迹相差较大。从出发到船舶艏向角达到90°时,两种模型的模拟结果吻合度很高,之后出现偏差。三自由度模型的模拟战术直径(4.35Lpp)和六自由度的(4.6Lpp)相比,小5%。对于回转速降时历,在出发后20 s内及60~80 s之间,速降时历吻合良好,此时,回转运动处于迎浪向横浪的转化过程中;在出发后20~60 s之间及80 s之后,三自由度的模拟回转速度较六自由度的大,特别是80 s之后,两者的差距达0.03 m/s,相对六自由度模拟的回转,稳定后航速差异达5%。
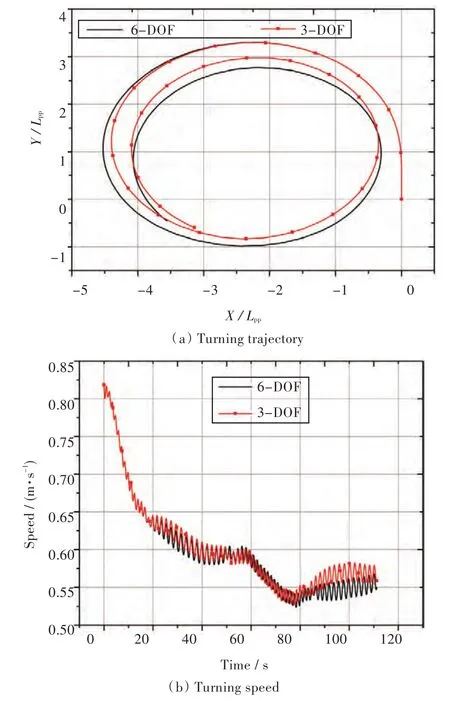
图8 T7工况下三自由度和六自由度模拟结果对比Fig.8 Comparisons of 3-DOF&6-DOF turning circle simulation results in case T7
2.4.2 水平面运动对摇荡运动的影响
下面,以回转横摇运动为例讨论水平面运动对摇荡运动的影响,如图9、图10所示。
由图9可以看出,在高频波浪条件(T1)下,有、无二阶波浪漂移力对回转横摇运动影响很大。在有漂移力的情况下,由于受横摇二阶波浪漂移力和船舶位置变化的双重作用,横摇平均值长周期变化相对的正弦曲线幅度约为1.5°,和无漂移力情况下的结果相比大1°;在有漂移力的情况下,回转横摇运动幅值比无漂移力情况下的结果大0.7°,在无漂移力情况下计算得到的回转横摇幅值差异更高,达20%;在有漂移力的情况下,迎浪回转横摇运动振荡比无漂移力情况下的结果更剧烈。究其原因:一是横摇二阶波浪漂移力的作用;二是在高频波浪条件作用下,一阶波浪力小,船舶摇荡运动幅度不大,受干扰影响大,二阶波浪漂移力大,船舶漂移运动剧烈,回转运动轨迹差别大,此时,两种情况下的船舶实时遭遇波情况和自身运动状态均不同,导致回转横摇运动结果差距较大。

图9 T1工况下有、无二阶波浪漂移力模拟结果对比Fig.9 Turning circle simulation results in T1 with or without drift force
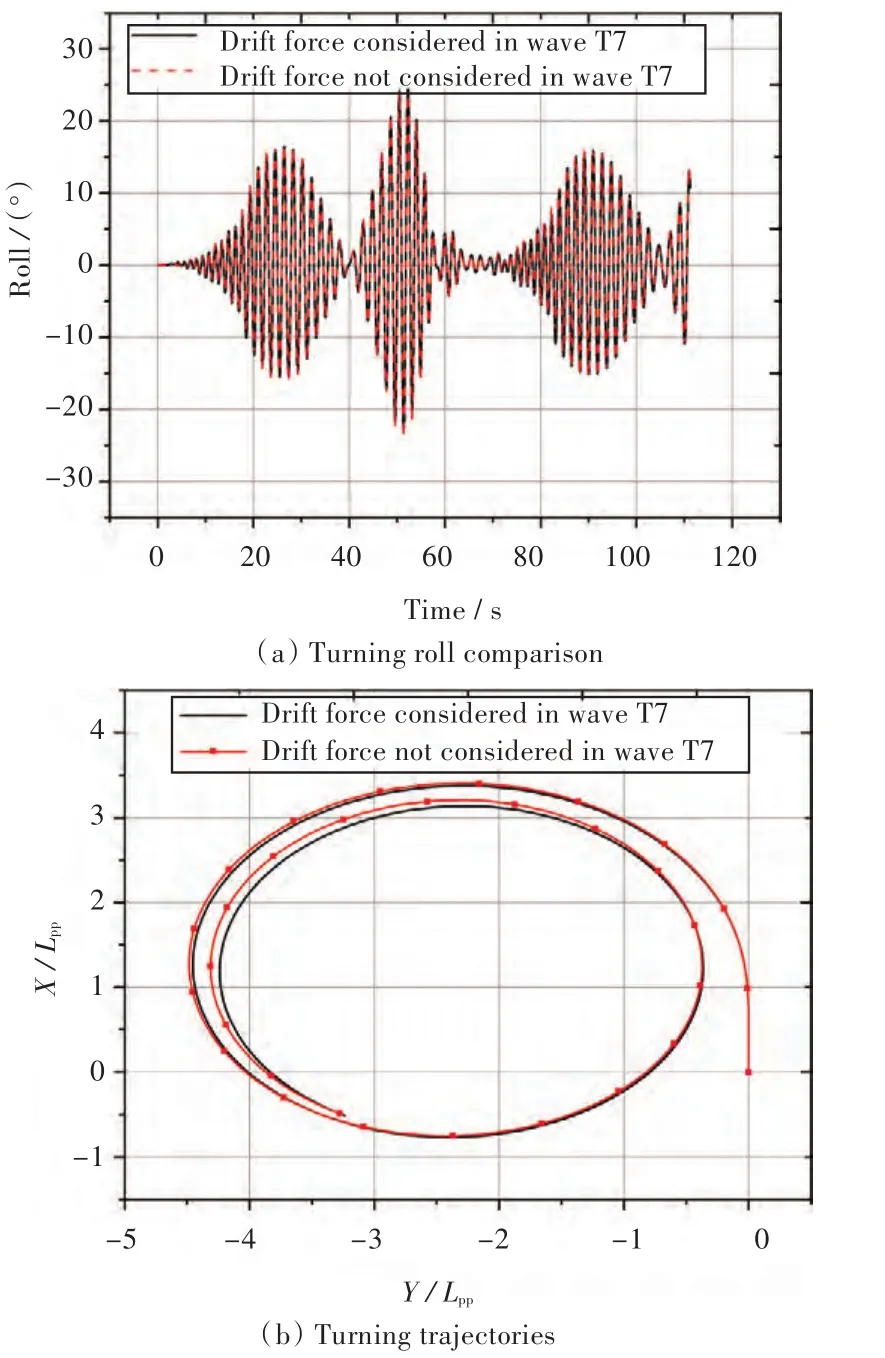
图10 T7工况下有、无二阶波浪漂移力模拟结果对比Fig.10 Turning circle simulation results in T7 with or without drift force
由图10可以看出,在低频波浪条件(T7)下,有、无二阶波浪漂移力对回转横摇运动影响不大,两种情况下的回转横摇运动时历曲线重合度很高,回转运动轨迹也基本吻合。
综上所述,以设置的工况条件为标准,在低频波浪条件下,摇荡运动对操纵运动的影响效果约为5%;而在高频波浪条件下,操纵运动对摇荡运动的影响效果则高达20%。
3 结 语
本文提出适用于船舶在波浪中运动的六自由度操纵运动模型,该模型能准确预报船舶六自由度的操纵和摇荡运动。对S175集装箱船在静水和规则波中的回转运动进行了数值模拟,计算结果表明,操纵运动与摇荡运动的耦合作用效果显著,六自由度的操纵运动模型十分必要。由于提出的波浪力模型是线性的,GM也是作为定值考虑,从理论上讲,此模型只适用于微幅波的情形。
[1]HIRANO M,TAKASHINA J,TAKAISHI Y,et al.Ship turning trajectory in regular waves[J].West Japan Society of Naval Architects,1980,60:17-31.
[2]KIJIMA K,FURUKAWA K Y.Ship maneuvering performance in waves[C]]//3rd International Stability Workshop,1997.
[3]安川宏纪.波浪中における船の操縦運動シミュレーション[C]//日本船舶海洋工学会論文集,2008:163-170.
[4]SKEJIC R,FALTINSEN O M.A unified seakeeping and maneuvering analysis of ships in regular waves[J].Journal of Marine Science Technology,2008,13(4):371-394.
[5]小濑邦治,汤室彰規,芳村康男.操縦運動の数学モデリの具體化[J].第三回操縦性シンポウム,1983:27-80.
[6]INOUE S,HIRANO M,KIJIMA K.Hydrodynamic derivatives on ship maneuvering[J].Inetrnational Shipbuilding Progress,1981,28(321):112-125.
[7]周昭明,盛子寅,冯悟时.多用途货船的操纵性预报计算[J].船舶工程,1983(6):21-29,36.
[8]TASAI F.On the damping force and added mass of ships heaving and pitching[R].California University Berkeley Institute of Engineering Research,1960.
[9]贾欣乐,杨盐生.船舶运动数学模型-机理建模与辨识建模[M].大连:大连海事出版社,1999:145-162.
[10]DAIDOLA J C,GRAHAM D A,CHANDRASH L A.A simulation program for vessel's manoeuvring at slow speeds[C]//Ship Technology and Research Symposium(STAR),1900.
[11]CUMMINS W E.The impulse response function and ship motions[R].Washington DC:David Taylor Model Basin,1962.
[12]苏威,马宁,顾解忡.VLCC波浪中操纵性数值预报与自航模试验验证[J].中国造船,2012,53(3):9-17.SU Wei,MA Ning,GU Xiechong.Numerical prediction of maneuverability in waves and free running model test for VLCC[J].Shipbuilding of China,2012,53(3):9-17.
