基于互相关的高精度多普勒频率变化率测量方法

何晓明，吴 琳

(中国电子科技集团公司第51研究所，上海 201802)

0 引言

在现代电子战中，近年兴起的机载单站无源快速定位技术所采用的是测向结合测距的定位方法。而利用多普勒频率变化率实现测距是一种快速高精度的无源定位技术。该技术的潜在优势在于，当受目标辐射源限制，机载单站无源系统截获次数很低时，依然可以通过较少的测量次数达到较高的测距精度。该技术对多普勒频率变化率的测量精度提出了较高的要求，并且成为影响定位精度的主要因素之一。传统的实现多普勒频率变化率测量的信道化、瞬时测频等测频方法需要大量的脉冲数据，再经过时间的积累处理得到的，耗费大量的硬件资源，同时计算量大、时间长、且测频精度不理想，离单站无源定位与跟踪技术的要求还有较大的差距。

有鉴于此，为克服上述现有技术存在的不足，提出了基于互相关的高精度多普勒频率变化率测量方法，以提高测量精度，减小运算量，同时简化系统设计，降低工程应用难度。

1 实现方法

1.1 数学模型

假定对方的雷达是PD雷达或高精度的相参雷达。

设雷达于0时刻发射信号，发射的信号为

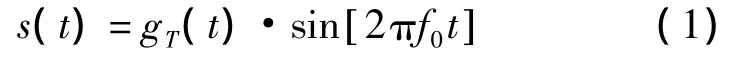
式中，f0为载频;gT(t)为周期为T的方波周期函数，方波的宽度为τ。

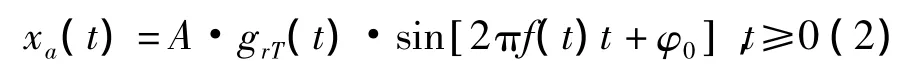
现对式(2)进行AD采样。假定采样间隔为ts，采样率为fs=1/ts，满足Nyquist带通采样定理。假定存在 N1，使

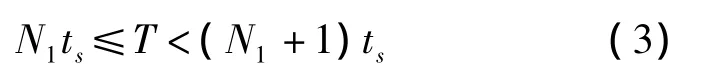
相应的采样的数据也写成K段，第k段数据为

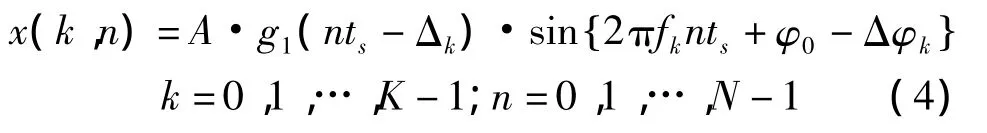
设ti时刻的脉组频率ft为

式中，f0为辐射源发射频率;fd，t为在 ti时刻由观测器和辐射源之间的相对运动引起的多普勒频移。设T为测量周期，则在ti+1=ti+T时刻的脉组频率ft+1为

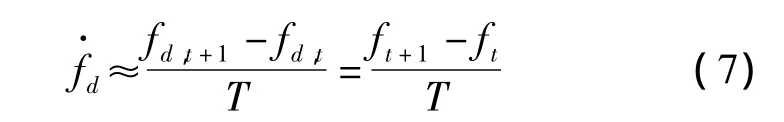
由式(7)可见，通过精确测量相邻脉组间信号频差(ft+1－ft)即可实现的高精度测量。

1.2 算法步骤

针对机载单站无源定位与跟踪这一特定的应用领域，提出了一种基于互相关的脉组间多普勒频率变化率的测量方法。具体实施步骤，如图1所示。

下面，结合具体实施方式详细介绍多普勒频率变化率的测量方法的各步骤。

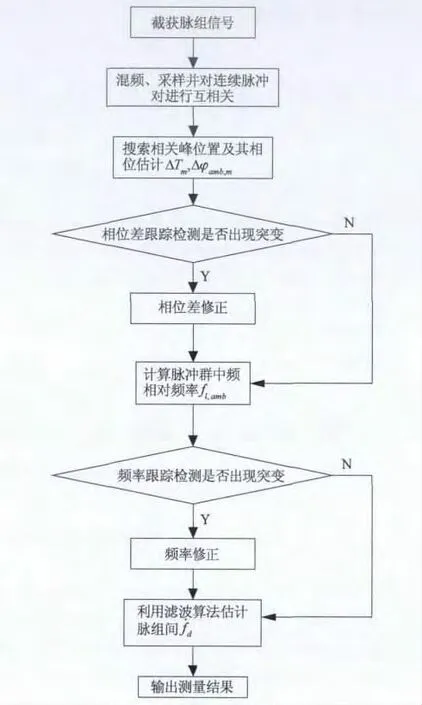
图1 多普勒频率变化率测量方法流程图

步骤1:截获雷达信号脉组。

利用数字干涉仪系统截获雷达信号脉组，具体是采用数字干涉仪系统中的宽带平面螺旋天线和接收机以一定的测量周期截获一系列脉组。此时，脉组间多普勒频率变化率等同于信号的相对频率变化率，故可用其频率变化率的测量值代替多普勒频率变化率的测量值。

步骤2:对所截获的脉组进行混频、采样处理并对脉组中的连续脉冲对进行互相关处理。

通过对脉组中的连续脉冲信号进行互相关处理，并构造同一脉组内各相邻脉冲间的互相关函数。定义第m个脉冲与第m+1个脉冲中频采样信号间的互相关函数为

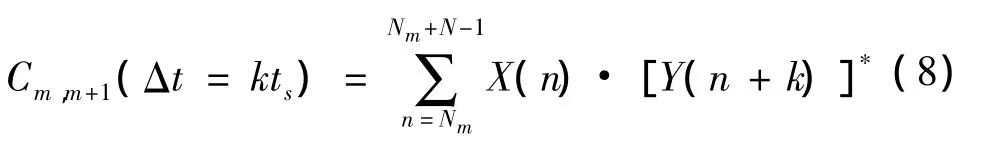
式中

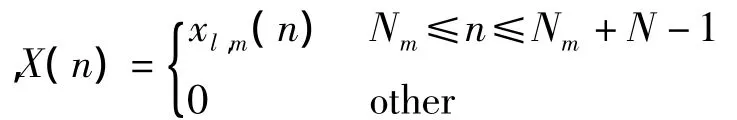
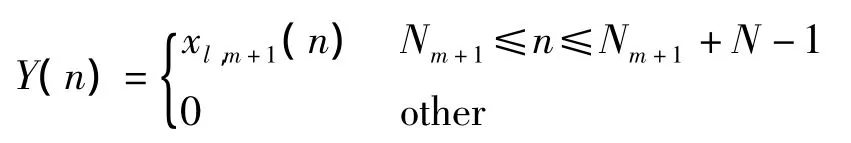
［］*表示求共轭。由两个脉冲间的相参性易知，互相关函数的模在时移Δt=kts=Tm+1－Tm时出现峰值，且峰值处 Cm，m+1(Δt)的相位即为这两个脉冲间的相位差。

步骤3:对互相关处理后的数据进行相关峰搜索，并记录相关峰的位置和相位估计值 ΔTm，Δφamb，m。

步骤4:进行相位差跟踪，并检测相位差是否存在突变，如果存在突变则对发生突变的脉冲对的相位差进行修正，如果不存在突变，则直接进入步骤5。

实际上，由于相位差以2π为周期，所以由上述互相关函数法测得的两个脉冲间相位差通常是包含模糊的。两个脉冲间的实际相位差为Δφm，可表示为 Δφm=(Δφm)mod2π +2kmπ(m=1，2，…，M －1)，Δφamb，m就是互相关函数的峰值得到的模糊相位，km是未知的模糊整数。

步骤5:基于脉冲对的相位差，计算脉组的中频相对频率 fl，amb。

由脉冲对间的相参性，中频频率可表示为

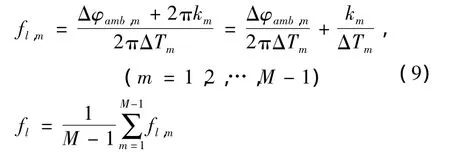
定义:

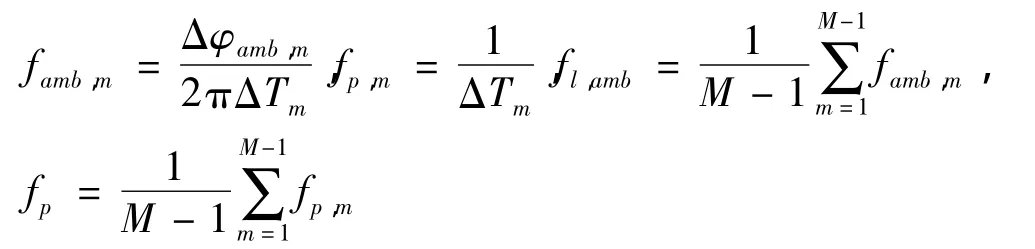
基于上述定义，可利用同一脉组内测得的M－1个时移和模糊相位差直接求得脉组的中频相对频率

步骤6:对脉组的中频相对频率fl，amb进行跟踪并检测是否存在突变，如果存在突变则对发生突变的中频相对频率进行修正。否则进入步骤7。

步骤7:基于脉组的中频相对频率 fl，amb，利用滤波算法估计脉组间多普勒频率变化率f·d，并输出结果。

在具体工程实施中，可利用Kalman滤波算法提取多普勒频率变化率。然后利用式(10)计算与目标的距离R，为

式中，d为天线阵元间距;φ·为相位差变化率;β信号到达角;f·d为频率变化率;(xi，yi)为载机在i时刻的位置坐标。

通过求得与目标辐射源的距离再结合到达方位角即可实现高精度的机载单站定位。

2 仿真分析结果

设辐射源的信号频率为9.5 GHz，脉冲重复周期为 50 μs，脉冲宽度为 1 μs，多普勒频率变化率为f·d，侦察设备测向精度为1°(r.m.s)，平台速度200 m/s，姿态误差为 0.1°(r.m.s)。利用该方法通过100次蒙特卡洛实验得到的多普勒频率变化率测量结果，见表1、表2。在信噪比在10 dB的情况下，t=30 s时根据测得多普勒频率变化率情况进行定位的结果，见表3、表4。

表1 多普勒频率变化率仿真测量结果(SNR=0 dB)

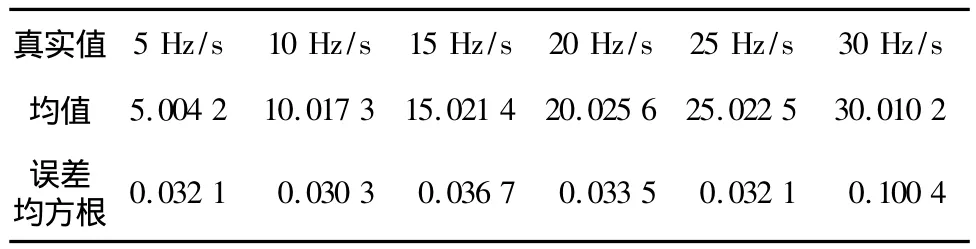
表2 多普勒频率变化率测量结果(SNR=10 dB)

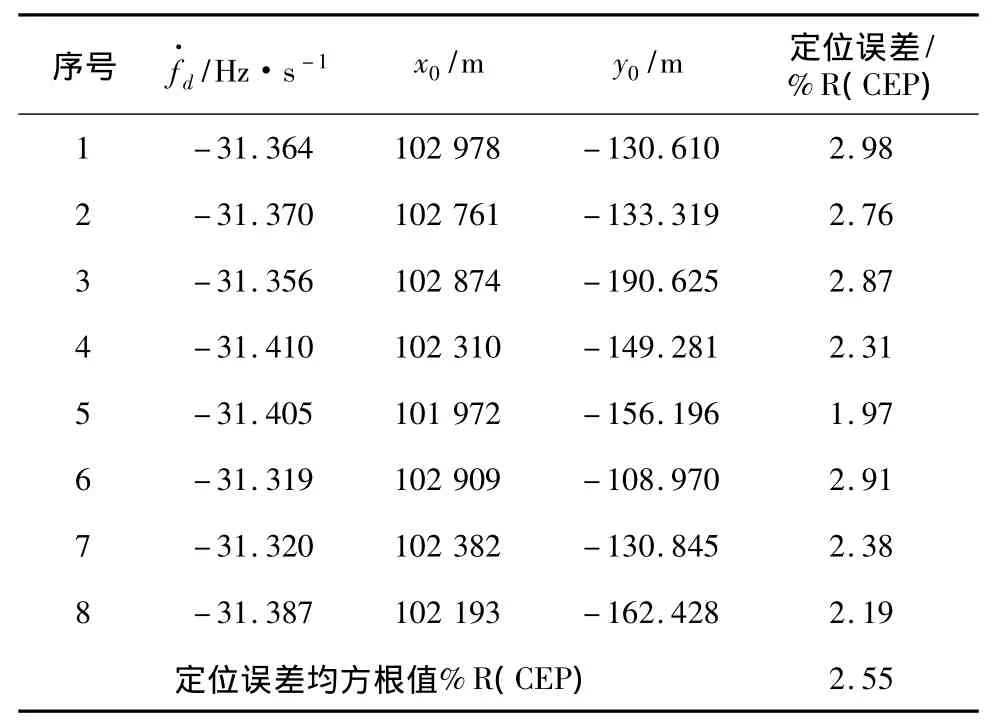
表3 距离100 km时的定位结果

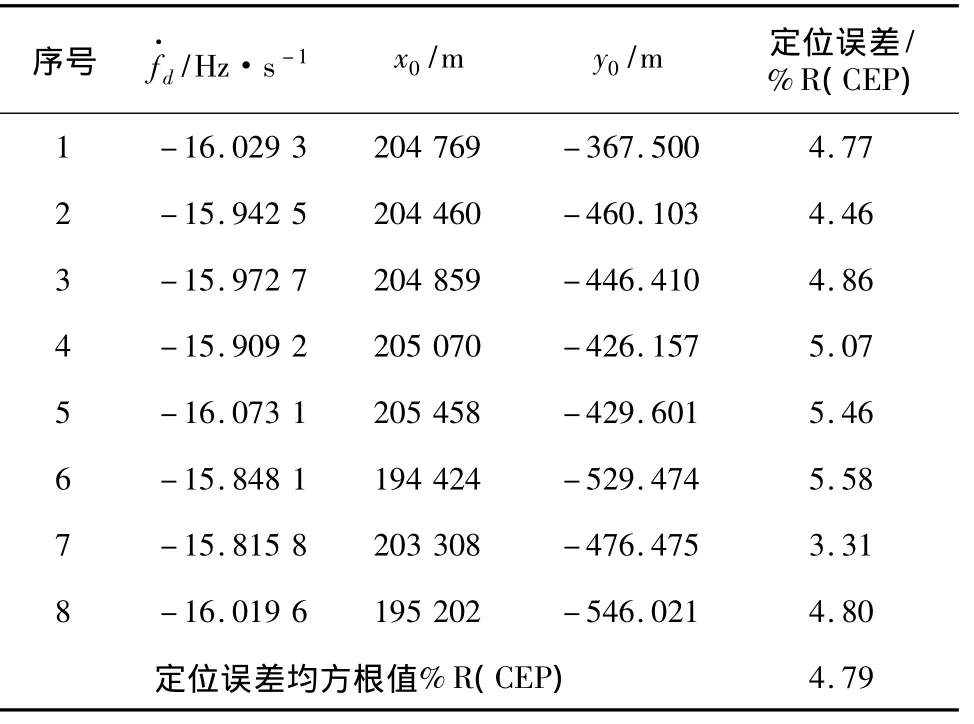
表4 距离200 km时的定位结果

利用该方法进行定位的GDOP示意图，如图2所示。从中可以看出各个点的定位精度分布情况，沿运动航迹的法线方向定位精度最高，其它方向逐渐降低。定位误差收敛曲线，如图3所示。

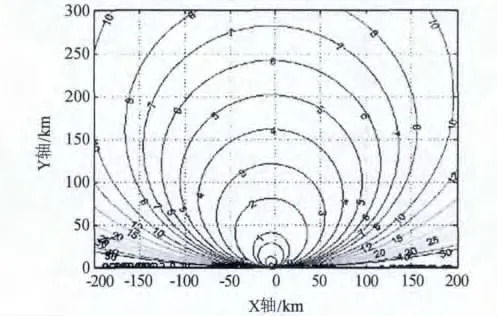
图2 定位GDOP示意图

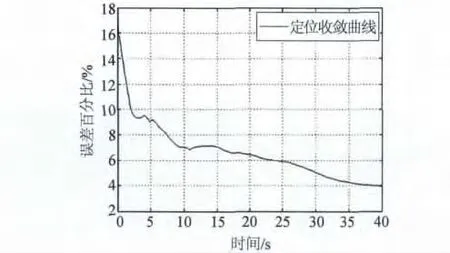
图3 定位百分误差收敛曲线图

通过以上的仿真分析，可以看出通过该多普勒频率变化率测量方法在测向精度达到指标为1°(RMS)的情况下，能够在30 s内对在航迹的法线方向200 km的辐射源实现5%的定位精度，通过适当增加观测时间和测向精度可收敛到更高的定位精度。

3 结语

提出了基于互相关的脉组间多普勒频率变化率测量方法，较直接测量信号频率的方法可以大幅度提高测量精度;同时，该方法还使系统的设备量和复杂程度大幅度降低，不仅简化了系统设备，所需的计算量也大大减小，实用性强。解决了传统的信道化、瞬时测频法等测频方法的测量精度难以满足单站无源快速定位系统要求的问题，为今后的工程应用和能力升级及扩展提供了良好的技术基础。

［1］安玮，孙仲康.利用多普勒变化率的单站无源定位测距技术［C］//雷达无源定位跟踪技术研讨会论文集，2001:41-45.

［2］郭福成，孙仲康.一种高精度测量脉冲序列频率的新方法［J］.制导与引信，2001(3):45-48.

［3］周亚强，曹延伟，程翥，等.脉冲群间多普勒频率变化率的高精度测量算法［J］.国防科技大学学报，2005(3):34-39.