数字端射阵列栅瓣抑制研究

常 仁，王小谟，刘姜玲，薛正辉

(1.北京理工大学信息与电子学院，北京 100081;2.中国电子科学研究院，北京 100041)

0 引言

端射天线结构简单，风阻小、成本低，作为雷达的发射和接收天线，可以大幅度缩减尺寸，实现雷达天线与载体的完美结合［1，2］。但是端射天线相比较于各种口径天线其增益不高，这一缺点制约了它在需要窄波束、高增益的雷达天线方面的应用。解决这一问题的办法就是以端射天线为阵元组成端射天线阵列。但是端射天线阵列由于本身体制问题引入阵元间复杂的互耦问题，导致端射天线组阵很难获得预期组阵高增益。通过拉大端射天线阵元间距组阵可以获得组阵高增益，但是又引入了栅瓣问题［3］。

下面对数字端射阵列(主要研究天线单元侧射组阵的情况，天线单元为平板端射天线，简称端射阵列)中栅瓣问题进行研究，提出一种基于最小二乘估计的虚拟内插阵元的方法，使虚拟阵列的阵元间距减小到(或者小于)0.5λ，从而使阵列栅瓣得到抑制。这对研究数字端射组阵有着重要意义。

1 最小二乘估计基本原理

最小二乘估计是一种很古老的估计方法［4，5］。这种方法可以追溯到1795年，当年高斯使用这种估计方法研究了行星的运动。在线性观测的情况下，由于它不需要任何先验知识，就可实现信号参量的估计，且易于实现，并能使误差平方和达到最小，所以最小二乘估计仍然是应用很广泛的一种估计方法［6］。

若被估计的参量有 p 个，用 β1，β2，…，βp表示，其观测数据 y与参量 β1，β2，…，βp之间服从如下的线性关系为

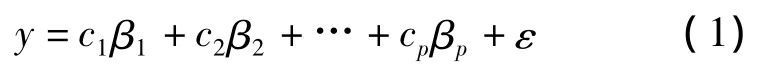
式中，c1，c2，…cp是已知的常系数;ε是观测噪声。若做了q次观测，则可以得到q个类似的线性方程，用向量和矩阵表示，可以写成

式中，

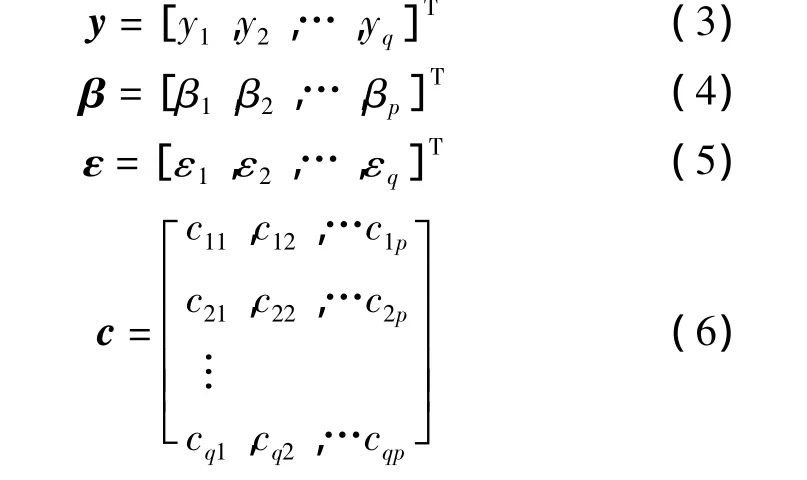
式中，[]T表示矩阵的转置。

此时，可以根据y来估计β。假定β的估计为β∧，为确定参数估计向量β∧，选择这样一种准则:使误差的平方和 R(β∧)=(y－cβ∧)T(y－cβ∧)最小。所求得的估计称为最小二乘估计。记作

当cTc为非奇异时，可得最小二乘估计量为

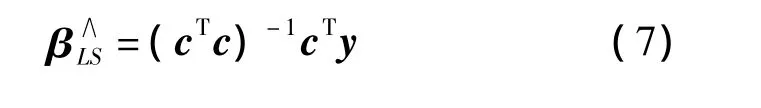
2 虚拟内插阵元算法

以下介绍如何基于最小二乘估计构建虚拟内插阵元算法。

在远场平面波假设条件下，以阵元数为N，阵元间距为d的等间距均匀线阵为例，实际阵列模型，如图1所示。在加性噪声背景下，入射信号为窄带信号s(t)，信号入射方向与阵列的法线方向夹角为θ。通过虚拟内插阵元的方法，在实际阵列间插入M个虚拟阵元形成均匀虚拟阵列，虚拟阵列阵元间距为dt;虚拟阵列模型，如图2所示。实际存在的阵元编号为 1，2，3，…，N。虚拟内插阵元的编号为 b1，b2，…，bM。

图1 实际阵列模型

以1号阵元为参考阵元，则j号实阵元的测量接收信号可表示为

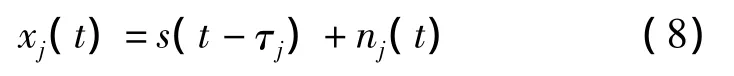
式中，τj=－(j－1)dsinθ/c为信号从参考阵元到达第j号阵元所需的时延;nj(t)为第j号阵元上的加性噪声，j=1，2，3，…，N。

对于窄带信号，用解析形式代替式(8)中的原始信号，阵元之间的延迟可以用相移来等效表示，所以可得到采样信号的解析表示为

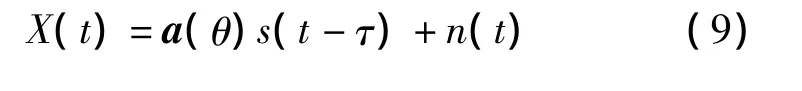
式中，

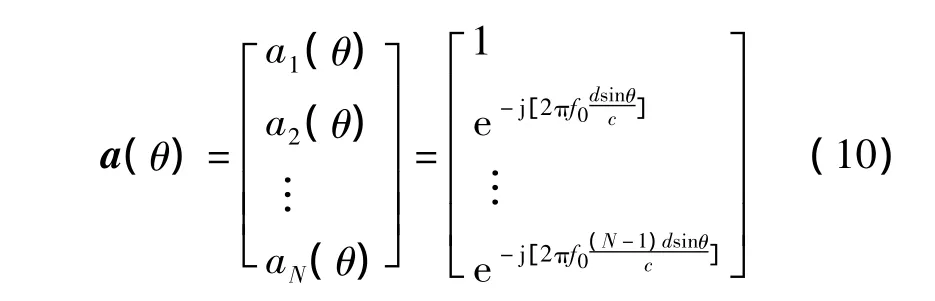
是均匀线阵对θ方向的响应向量。

现在以虚拟阵列的b1号阵元为例，推导基于最小二乘估计的虚拟内插阵元算法。假设观测模型是线性的，使参量 β=［β1，β2…βN］T满足

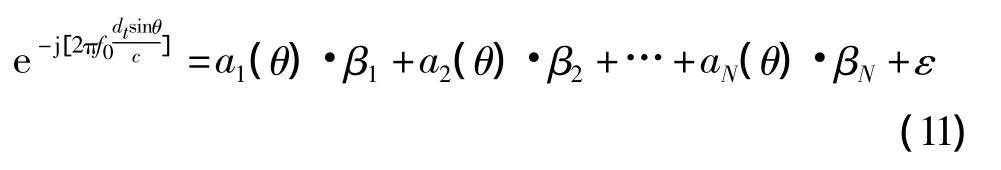
期望入射方向为θ，在θ两侧取q次观测值(q＞N)，分别为{θ1，θ2，…，θq}，则可以得到 q 个观测方程，写成向量形式为

式中，

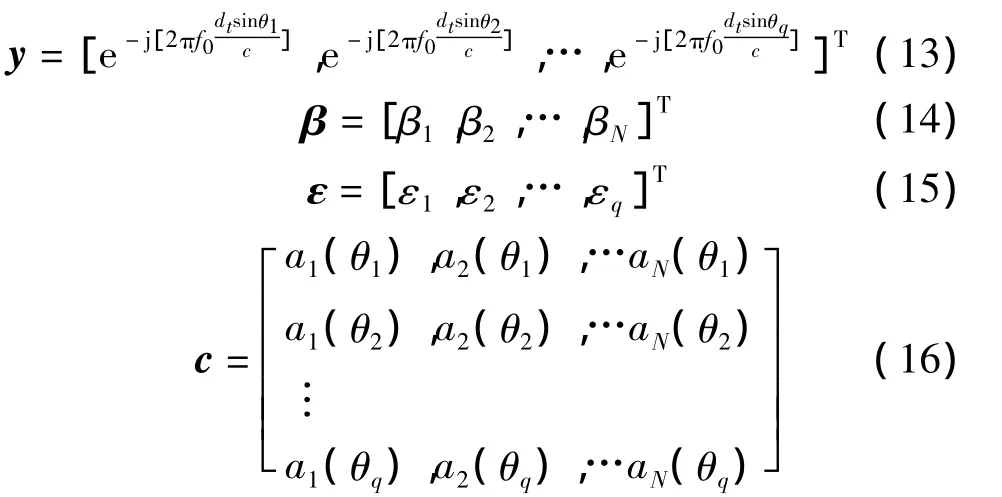
根据最小二乘理论，可以计算出最小二乘估计量为

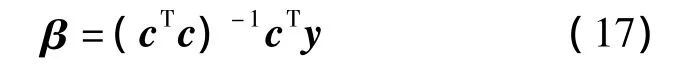
则b1号虚拟阵元上的接收数据为

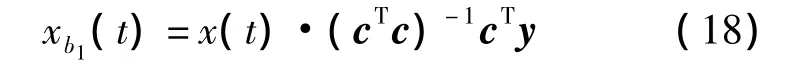
同理，可继续分别求出对应于这个采样时刻虚拟的b2，b3，…，bM号阵元上的接收的采样数据。假设在相邻实际存在的阵元间插入虚拟阵元，使虚拟阵列的阵元间距等于或者小于0.5λ，理论上虚拟阵列不会出现栅瓣。

3 虚拟端射阵列试验验证

在微波暗室开展测试，采用1个发射天线和4个接收端射天线组成接收阵列进行验证，通过对不同入射角的回波信号进行数字波束合成得到波束方向图。发射天线发射信号频率为3.2 GHz，为了实现不同入射角的效果，采用发射天线不动，接收阵列放置在转台上，－180°～180°旋转。发射天线和接收转台间距满足远场测试要求。

3.1 测试1

期望波束方向 θ0为 0°。实阵元编号:［1，2，3，4］，实阵元间距为1.5λ，虚拟内插3个阵元;虚拟阵元编号:［5，6，7］，虚拟阵元间距:0.75λ。实阵列模型，如图3所示;虚拟阵列模型，如图4所示。根据实测回波数据，对实阵列进行波束合成得到实阵列方向图。利用基于最小二乘估计的虚拟内插阵元算法计算出虚拟阵元的接收数据，然后进行波束合成得到虚拟阵列方向图称为仿真值。利用虚拟阵元在阵列各个位置的回波数据进行波束合成形成的虚拟阵列方向图称为实测值。实阵列方向图，虚拟阵列方向图仿真值和实测值对比，如图5所示。

图3 实际阵列模型

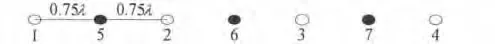
图4 虚拟阵列模型

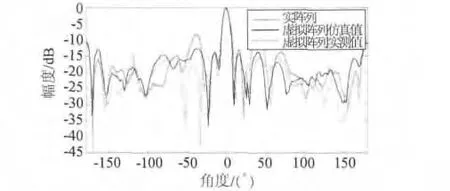
图5 归一化实阵列，虚拟阵列方向图仿真值与测试值对比

从图5中可以看出，实阵列栅瓣位置在±44°位置，栅瓣电平为－8.35 dB。在栅瓣位置，虚拟阵列仿真值为 －12.21 dB，下降了 3.86 dB，栅瓣得到有效抑制。

3.2 测试2

为了研究内插不同的虚拟阵元数对栅瓣的影响，开展试验。期望波束θ0为0°，实阵元编号:［1，2，3，4］，实阵元间距为 1.5λ，虚拟内插 6 个阵元;虚拟阵元编号:［5，6，7，8，9，10］，虚拟阵元间距为0.5λ，实阵列模型。如图3所示，虚拟阵列模型如图6所示。实阵列方向图，虚拟阵列方向图仿真值和实测值对比，如图7所示。

图6 虚拟阵列模型

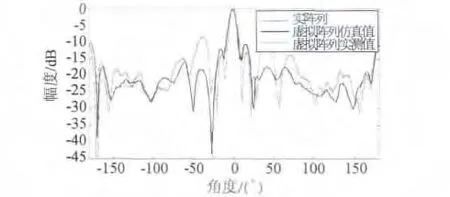
图7 归一化实阵列，虚拟阵列方向图仿真值与测试值对比

3.3 测试3

期望波束 θ0为0°，实阵元编号:［1，2，3，4］，实阵元间距为1.5λ，虚拟内插9个阵元;虚拟阵元编号:［5，6，7，8，9，10，11，12，13］，虚拟阵元间距为0.375λ。实阵列模型如图3所示;虚拟阵列模型如图8所示;实阵列方向图，虚拟阵列方向图仿真值和实测值对比，如图9所示。

图8 虚拟阵列模型

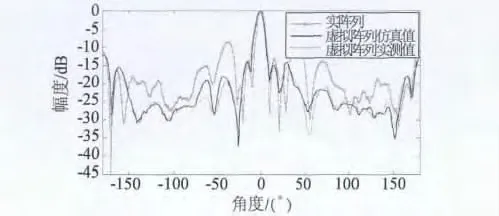
图9 归一化实阵列，虚拟阵列方向图仿真值与测试值对比

3.3 测试结果分析

不同虚拟内插阵元个数方向图对比，如图10所示;峰值副瓣电平对比结果见表1。随着虚拟内插端射天线阵元个数的增加，栅瓣明显被抑制，峰值副瓣电平降低越多。在相邻两个实阵元间内插3个虚拟阵元，虚拟端射阵列保持了实端射阵列高增益，而实阵列峰值副瓣电平为－8.35 dB，下降到虚拟阵列峰值副瓣电平为－18.25 dB，栅瓣得到有效抑制。

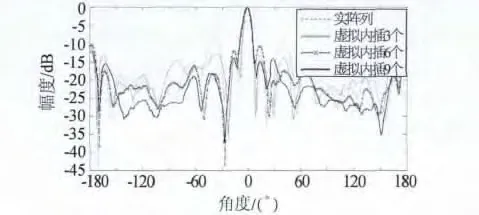
图10 不同虚拟内插阵元个数方向图对比

表1 峰值副瓣电平对比结果

从图5，图7和图9可知，测试值和仿真值大体一致。造成误差的原因有三个:(1)天线位置的误差，由于接收天线间距精度为0.1 mm，而测试时天线布置的刻度精度为1 mm;(2)回波数据误差，由于转台自动采集的方式造成;(3)算法误差，随着虚拟阵元数目的增多，虚拟阵元的数据误差越来越大。在误差允许的范围内，测试结果验证了基于最小二乘估计的虚拟内插阵元算法的可行性和正确性。

4 结语

通过拉大端射天线阵元间距组阵可以获得组阵高增益，但是引入栅瓣问题。提出了一种基于最小二乘估计的虚拟内插阵元算法来实现栅瓣抑制，使虚拟端射阵列的阵元间距减小到(或者小于)0.5λ，这样栅瓣得到抑制。试验结果表明:随着虚拟内插端射天线阵元个数的增加，栅瓣明显被抑制，峰值副瓣电平降低越多。在相邻两个实阵元间内插3个虚拟阵元，虚拟端射阵列保持了实端射阵列高增益，而实阵列峰值副瓣电平为－8.35 dB，下降到虚拟阵列峰值副瓣电平为－18.25 dB，栅瓣得到有效抑制。试验结果验证了基于最小二乘估计的虚拟内插阵元算法的可行性和正确性。在以后的工作中，如何减小算法误差和更好的虚拟内插算法是下一步的研究重点。

［1］刘忠凯.端射天线辐射机理和辐射高增益的研究［D］.北京:北京理工大学电子工程系，2008.

［2］姚国伟.高增益端射天线阵列研究［D］.北京:北京理工大学信息与电子学院，2010.

［3］刘姜玲，刘姜涛，王小谟.平板端射阵列栅瓣抑制研究［J］.微波学报，2011，10:149-151.

［4］胡鹏，杨士莪，杨益新.基于最小二乘估计的虚拟单元波束形成仿真［J］.计算机仿真，2007，24(1):323-325.

［5］吕峰洁，张永瑞，杨刚.基于最小二乘法的气体传感器精度的研究［J］.电子科技，2007，20(6):40-42.

［6］胡鹏.虚拟单元波束形成方法研究［D］.西安:西北工业大学，2006.