主应力轴旋转对黄土动模量和阻尼比的影响
2014-11-09胡孝彭
胡孝彭
(重庆水利电力职业技术学院,重庆 402160)
在我国的中西部地区,黄土分布较为广泛。统计显示,2008年,我国5级以上地震累计发生97起,大部分集中在中西部地区,2012年全国地震累计发生19次5级以上地震,其中中西部地区最为频繁。由于黄土地区地震多发且烈度较大,地震作用给当地人民的生命财产安全屡屡带来灾难性的破坏。为此,动荷载作用下黄土地区的工程问题引起了国内诸多专家学者的关注,并开展了一系列的研究工作[1,2]。
在实际的岩土工程中,地震荷载、交通荷载和波浪荷载等都会涉及到主应力轴旋转[3],而常规的振动三轴试验无法模拟该状态下土体的工程动力特性。鉴于此,本文采用DTC-199型周期扭转荷载三轴仪,对不同初始状态下的黄土进行动扭剪试验,模拟由主应力轴旋转引起的复杂应力状态,以期更好地研究非饱和黄土的动剪模量和阻尼比的变化规律,为黄土地区工程的设计和动力稳定分析提供可靠依据。
1 试样仪器与方案
1.1 试样的制备
试验所用黄土土样含水率为19%,比重为2.7,孔隙比为1.02,液限为 29%,塑限为 17.5%,干密度为 1.52 g/cm3,最大干密度为1.67 g/cm3,其中粘粒含量为20.7%,粉粒含量为62.8%,砂粒含量为16.5%。
试样为空心圆柱形,外径70 mm,内径30 mm,高100 mm,高径比为1.43,将块状土样放在橡皮板上用木碾碾散后过2 mm筛,将过筛后的土样或风干或使用喷雾器喷洒一定量的水分使其达到目标含水率,先用相应的三轴压样器分4层压制而成圆柱形,再用刀具掏空制成空心圆柱形试样,套上保鲜膜放入密闭缸中以备使用。
1.2 试验仪器
本试验采用DTC-199型周期扭转荷载三轴仪,由主机、压力系统、动力控制系统和测量系统四大部分组成,可以施加轴力W、扭矩M、内室压力pi和外室压力p0并自动采集试验数据。参照土工试验规程[4]以及文献[5]中空心扭剪三轴试验进行操作。先在不排水条件下,缓慢施加内侧压力、外侧压力和轴力至目标值,然后上下排水固结。如需施加扭矩,待固结完成后施加扭矩至目标值。试验采用的动荷载频率为1 Hz,在试样顶端逐级施加周期水平动剪应力,直至试样破坏为止。
1.3 试样应力状态
为分析试样的应力状态,取试样上一小单元,如图1所示,W产生 σz,M 产生 τzθ,pi和 p0引起 σr和 σθ。为方便试验控制,定义以下四个控制参数:主应力方向角α、中主应力系数b、平均主应力p、广义剪应力q和偏应力比η。

图1 应力状态分析
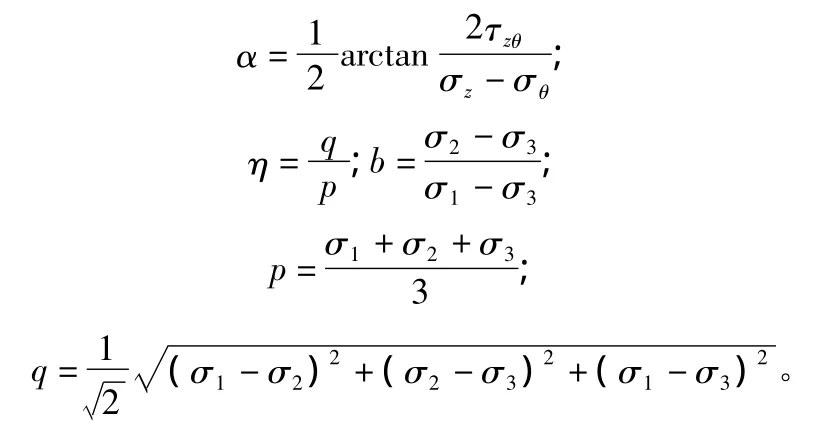
为实现由主应力轴旋转引起的复杂应力状态,可先确定控制参数 α,b,p,η 的值,然后通过进一步的换算[10],从而整理得出要施加的轴力W、扭矩M、内室压力pi和外室压力p0的大小。具体的试验方案如表1所示。

图2 W—G0关系曲线(α=45°,η=0.43,b=0.5)

图3 ρd—G0关系曲线(α=45°,η=0.43,b=0.5)

表1 试验方案
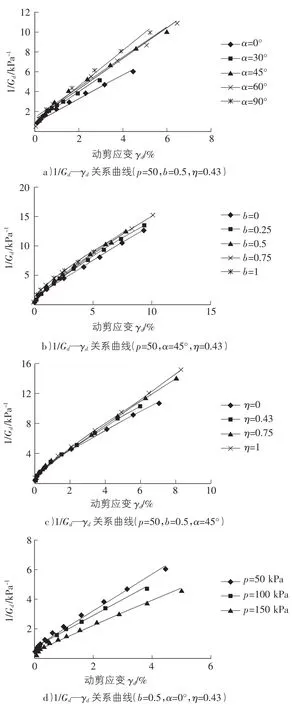
图4 1/Gd—γd关系曲线图
2 试验结果分析
2.1 主应力轴旋转对黄土动剪切模量的影响
动剪切模量Gd是指土体产生单位动剪应变所需的动剪应力,即τd/γd。大量研究表明,在动荷载作用下黄土的应力应变关系曲线呈现双曲线型[6]:
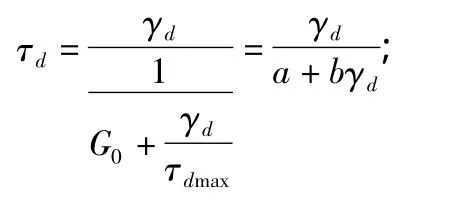

其中,τd为动剪应力;τdmax为最大动剪应力;γd为动剪应变;Gd为动剪切模量;a,b分别为1/Gd—γd关系曲线的纵轴截距和斜率;G0为最大动剪切模量,可以从1/Gd—γd关系曲线求得。
图2为不同含水率下黄土最大动剪切模量的变化曲线,从图中可以看出,在其他条件相同的情况下,含水率越大,黄土的最大动剪切模量越小,说明含水率与最大动剪切模量息息相关,这主要是因为含水率直接关系到黄土颗粒之间的联结强度,决定着黄土的结构性,含水率较低时,抵抗剪切变形的能力相应较强,图3为不同干密度下黄土最大动剪切模量的变化曲线,由图3中可知,黄土的最大动剪切模量随试样干密度的增大而增大。综合图2,图3可以看出,同一含水率(干密度)下,黄土的最大动剪切模量随初始平均主应力(固结应力)的增大而增大。
图4a)~图4d)分别是非饱和黄土在不同α,b,p,η下的关系曲线。从图中可以看出:不同的 α,b,p,η下的1/Gd—γd关系曲线都能较好用直线拟合,说明试验结果与上述双曲线模型的吻合较好。同时,在动剪应变幅较小的范围内,不同 α,b,p,η下的1/Gd—γd关系曲线区别不大,即 α,b,p,η 对 1/Gd—γd关系曲线的影响很小或影响程度较小。然而在大应变幅(≥1%)下,动剪切模量随着α,p的增大而减小。
2.2 主应力轴旋转对黄土阻尼比的影响
土体在周期动荷载作用下的应力应变关系曲线表现出一定的滞后性,阻尼比实际上反映了能量在土体内部受阻力影响而损失的动力特性。
土体的阻尼比λ的计算公式为:

其中,ΔW为滞回曲线所包围的总面积;W为图5中阴影部分的面积。

图6 不同干密度下γd—λ关系曲线
图6,图7为非饱和黄土在不同干密度与含水率下阻尼比和动剪应变的关系曲线,从图中可以看出,总体上,阻尼比随着动剪应变的增大表现出不断增大的趋势,值得注意的是,动剪应变较小时曲线走势较陡,至某一动剪应变幅值后,曲线趋于平缓,阻尼比的大小趋近于某一定值,还可以发现,黄土的阻尼比一般在0.15~0.30之间。同时,随着动剪应变的变化,表现出干密度越小,含水率越大,阻尼比越大的趋势。

图7 不同含水率下γd—λ关系曲线
图8a)~图8d)分别为半对数坐标中不同α,b,p,η下非饱和黄土的γd—λ关系曲线。从图中可以看出,不同的α,b,p,η下的黄土的阻尼比随动剪应变的增加总体呈现出不断增大的趋势,并且表现出较好的相关性(相关系数 R2≥0.809),这说明 α,b,p,η对非饱和黄土的阻尼比基本没有影响。
3 结语
本文采用DTC-199型周期扭转荷载三轴仪,对不同初始状态下的黄土进行动扭剪试验,研究主应力轴旋转对黄土的动剪切模量和阻尼比的影响规律,结果表明:
1)使用动扭剪三轴仪可以有效模拟地震荷载中主应力轴旋转现象研究该状态下黄土的工程动力特性。

图8 γd—λ关系曲线图
2)黄土的最大动剪切模量随含水率的减小而增大,随着干密度的增大而增大;在剪应变幅较大的范围(≥1%),黄土的动模量随平均主应力p和主应力方向角α的增大而增大,随中主应力系数b和偏应力比η的增大而减小。
3)黄土的阻尼比随含水率增大而增大,随干密度的增大而减小,其值大小在0.15~0.30之间,随动剪应变增大趋于稳定。在半对数坐标系中,不同p,α,η和b下的阻尼比与动剪应变之间具有良好的线性关系。
[1]王兰民,石玉成,刘 旭,等.黄土动力学[M].北京:地震出版社,2003.
[2]骆亚生,谢定义.黄土破坏动应力和初始动模量的一种经验估算公式[J].西北水资源与水工程,2000,11(3):6-10.
[3]Ishihare K.Soil response in cyclic loading induced by earthquakes,traffic and waves[C]//Proceedings of the 7th Asian Regional Conference on Soil Mechanics and Foundation Engineering.Haifa,Israel:International Academic Publishers,1983:42-66.
[4]SL 237-1999,土工试验规程[S].
[5]朱思哲,刘 虔,包承纲,等.三轴试验原理与应用技术[M].北京:中国电力出版社,2003.
[6]HARDIN B O,DRNEVICH V P.Shear modulus and damping in soils:design equation and curves[J].Journal of Soil Mechanics and Foundation Division,ASCE,1972,98(7):667-692.
