辊子压带式带式输送机的动态特性
2014-11-08周广林韩瑞飞
周广林,韩瑞飞
(黑龙江科技大学机械工程学院,哈尔滨150022)
辊子压带式带式输送机的动态特性
周广林,韩瑞飞
(黑龙江科技大学机械工程学院,哈尔滨150022)
为提高设备运行的可靠性及安全性,利用Pro/E对辊子压带式带式输送机进行建模,通过ADAMS对模型进行不同工况下的动态特性分析。讨论了输送带刚度、阻尼系数、压辊分布、带速以及输送机对辊子压带式带式输送机动态特性的变化规律。分析结果表明,适当的增大输送带的刚度和阻尼系数,可以有效地减小启动过程中输送带的波动幅度;带速的增加,输送机系统的不稳定性增大;输送带的最大张力值与输送量近似成线性关系;输送距离与输送机系统的振动特性关系显著;适当地加大压辊的间距,还可以在一定程度上降低成本。虚拟样机技术对辊子压带式带式输送机进行动态分析的方法是可行的,为高带速、长运距辊子压带式带式输送机的发展提供了理论的依据。
带式输送机;辊子压带式;动态特性; ADAMS
收稿日期: 2013-12-10
第一作者简介:周广林( 1961-),男,吉林省怀德人,教授,博士,研究方向:机械电子及基于声强测量的宽带声全信息技术,E-mail: guanglinzhou@163.com。
0引言
压带式带式输送机是为增大带式输送机输送倾角而设计的。根据压紧方式的不同,主要有自重压带式、刮帘压带式、加载压带式、张紧环压带式等[1]。它与普通带式输送机相比有以下特点: ( 1)输送倾角大,甚至可以实现90°倾角的输送,在垂高一定的情况下,缩短了输送机的整体长度,降低了设备成本; ( 2)密闭输送,避免散状物料在输送过程中出现洒落、泄漏、扬尘等现象; ( 3)运行速度高,输送能力大。
其低运量、短运距的带式输送机的设计,利用常规的静态设计方法所得的结果及运动特性可以满足其要求。但是,对于长距离、大运量、高带速及工作环境相对复杂的大型带式输送机,输送机的动态性能对整个系统的安全性及可靠性影响较大,成为输送机设计的关键问题[2-5],必须考虑带式输送机的动态特性,进行准确的动态分析与设计。
笔者利用多体动力学分析软件ADAMS,对辊子压带式带式输送机的运行过程进行动态分析,旨在找到对输送机动态性能影响较大的运行参数、性能参数,并通过调整这些参数,改善输送机的动态性能,提高设计效率和设计精度,节约生产成本,提高设备运行的可靠性及安全性。
1动力学建模
1. 1 工作原理
压带式带式输送机由上、下两条闭环输送带系统组成。压带式带式输送机是靠物料与输送带之间的摩擦力作用来防止物料下滑,保证物料的稳定输送。下带为承载带,起承载作用;上带为覆盖带,主要是产生夹持作用力,以夹紧物料,阻止物料的下滑和滚动,实现物料与输送带同步运行,完成物料的输送。辊子压带式带式输送机,是在覆盖带上加上压辊,通过压辊的压力作用增加物料与输送带之间的正压力,从而使物料与输送带之间的摩擦力增加,有效地防止物料的下滑。
对辊子压带式带式输送机的虚拟样机模型进行动态分析,主要是为了研究运行速度较高时输送带的振动、张力波动问题。当运行速度较高时,整个输送机系统的动态特性会表现的越来越明显,对输送带及机架的损坏也大幅度地增加。输送带成本约占整机成本的一半,是辊子压带式带式输送机的关键部件。输送带本身的黏弹特性,再加上多种因素的共同作用,在加减速等不稳定工况下运行时,使其张力波动比较大,严重时会造成输送机系统损坏,所以对输送机动态特性的研究显得非常重要。
1. 2 模型的尺寸及参数
经过简化,所建立的辊子压带式带式输送机的虚拟样机模型,主要包括传动滚筒、改向滚筒、滚筒轴、承载带、覆盖带、托辊、压辊等部件。图1为经过简化后所建立的辊子压带式带式输送机的虚拟样机模型,具体参数为:传动滚筒与改向滚筒的直径D均为300 mm,定义为刚体,托辊直径Dt=60 mm,压辊直径Dy= 120 mm,输送倾角为45°,输送带宽度b =1 m,输送带线密度ρl= 7. 29 kg/m,带厚d = 10 mm,输送带的刚度系数k =1.25×107N/m,阻尼系数δ=1.0×105Ns/m;传动滚筒、改向滚筒分别采用附胶面和光面,它们与输送带间的摩擦系数μ分别为0. 4、0. 35;承载带与覆盖带上所施加的预紧力均为18 kN,压辊产生的压紧力为1 kN。由于输送距离越长,带块数越多,运算时间越长,为了提高运算效率,这里设输送长度L =8 m,启动时间t =4 s。
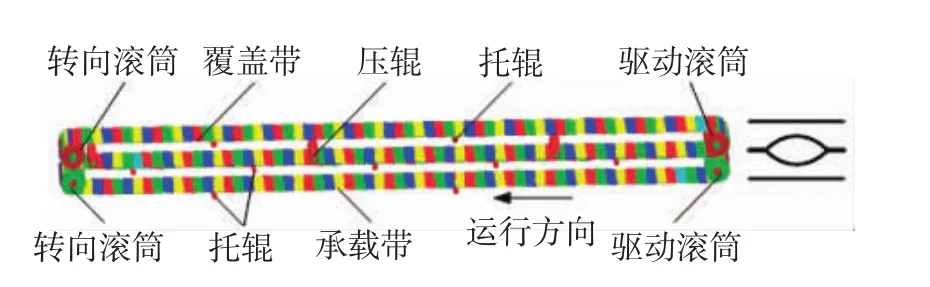
图1 辊子压带式带式输送机的虚拟样机模型Fig.1 Virtual prototype model of roller sandwich belt conveyor
输送带本身的黏弹性,使得在建模时必须对输送带进行柔性化处理。ADAMS中对柔性体的处理主要有两种方法:一种是基于有限元思想,将输送带离散成多个小带块,然后在带块与带块之间建立柔性连接,以模拟带的柔性。另外一种方法是利用ADAMS软件本身所提供的柔性体理论来实现输送带的柔性化。第一种方法简单,但它是第二种方法的基础,由于第二种方法的精度高,这里选择第二种方法。
文中所建的辊子压带式带式输送机模型由多个柔性化的带块所组成,各个带块之间通过柔性连接建立约束关系。利用ANSYS软件生成带块的模态中性文件,将其输入到ADAMS中,以取代所建立的刚性体带块,并将其与其他构件之间建立约束关系,从而达到将输送带柔性化的效果。
1. 3 模型的建立
辊子压带式带式输送机比较复杂,在实际应用中,布置方式、张紧方式以及驱动方式也是多样化的,如倾角大小、压辊数量与分布等也不相同。因此,要完成对辊子压带式带式输送机虚拟样机系统的建模,就必须在CAD软件的基础上,建立起输送机系统中不同部分的模块图库,如压辊与托辊的设计、过渡段的设计、提升段的设计、机架设计等。建立参数化的图库模块,能够使用户根据各自的需要组合成不同的输送机的样机模型。
辊子压带式带式输送机是一个比较复杂的机械系统,如果按照实际尺寸建立模型,其几何尺寸将非常大,这样将会在很大程度上延长计算所需的时间。因此,文中对所建模型进行了一定程度的简化。
在对辊子压带式带式输送机进行几何建模时,主要是借助Pro/E软件,即在Pro/E软件环境下完成对辊子压带式带式输送机系统的三维实体建模。在Pro/E中完成建模后,将文件另存为.xt格式,然后利用ADAMS和Pro/E之间的标准图形接口,将文件输入到ADAMS中,对仿真结果进行分析,然后在ADAMS中完成对各构件质量属性的设置,以及对输送带的柔性化处理。
1. 4 接触副的建立
接触力是一种特殊的力。它产生于两构件表面发生接触时的接触位置,包括间断性接触和连续性接触两种。ADAMS/View主要是通过补偿法和冲击函数法来计算接触力[6-7]。当构件间发生接触后,就会产生法向和切向上的作用力与反作用力,在切向力的作用下,会使构件间产生摩擦力。摩擦力的计算可运用库仑定律获得。
两构件间的接触是通过其几何元素来实现的,文中所建模型的接触副是采用Solid-Solid的类型,通过接触副来模拟带块与滚筒、托辊以及压辊之间的摩擦力。
2动态特性分析
2. 1 启动方式
带式输送机在启动过程中,带的张力变化复杂,启动速度影响整个系统的稳定性和安全性。常用的有HARRSION曲线、NORDELL曲线和余弦曲线等,其中HARRSION速度启动曲线是最常用的一种[8]。
2. 2压辊间距、输送带刚度及阻尼对输送机动态特
性的影响
2. 2. 1 压辊间距
如何在保证物料安全输送的同时,又能保证压辊布置不会对输送机的动态特性造成负面影响,这是辊子压带式带式输送机必须研究的问题。输送机运行速度v =4 m/s。图2为不同压辊间距下输送带的张力曲线,用曲线ceshidian1-Force.Mag( F1)、ceshidian2-Force.Mag( F2)分别表示测试点1、2所在位置的张力变化。(测试点1为覆盖带进入承载段的起始点,测试点2为承载带进入承载段的起始点,带块1、2分别为覆盖带与承载带上即将进入与滚筒接触段的同步带块。)
如图2所示,对于覆盖带上的测试点1,压辊间距ly= 2. 5 m时,张力在t = 1. 6 s时达到最大值13. 0 kN;压辊间距ly=3 m时,张力在t =1. 9 s时达到最大值12. 1 kN;压辊间距ly= 3. 5 m时,张力在t =1. 8 s时达到最大值11. 7 kN。从数据上看,随着压辊间距的增加,启动过程中测试点1的最大张力值及其变化幅度减小,最大张力值的变化与压辊间距的变化不成线性关系。
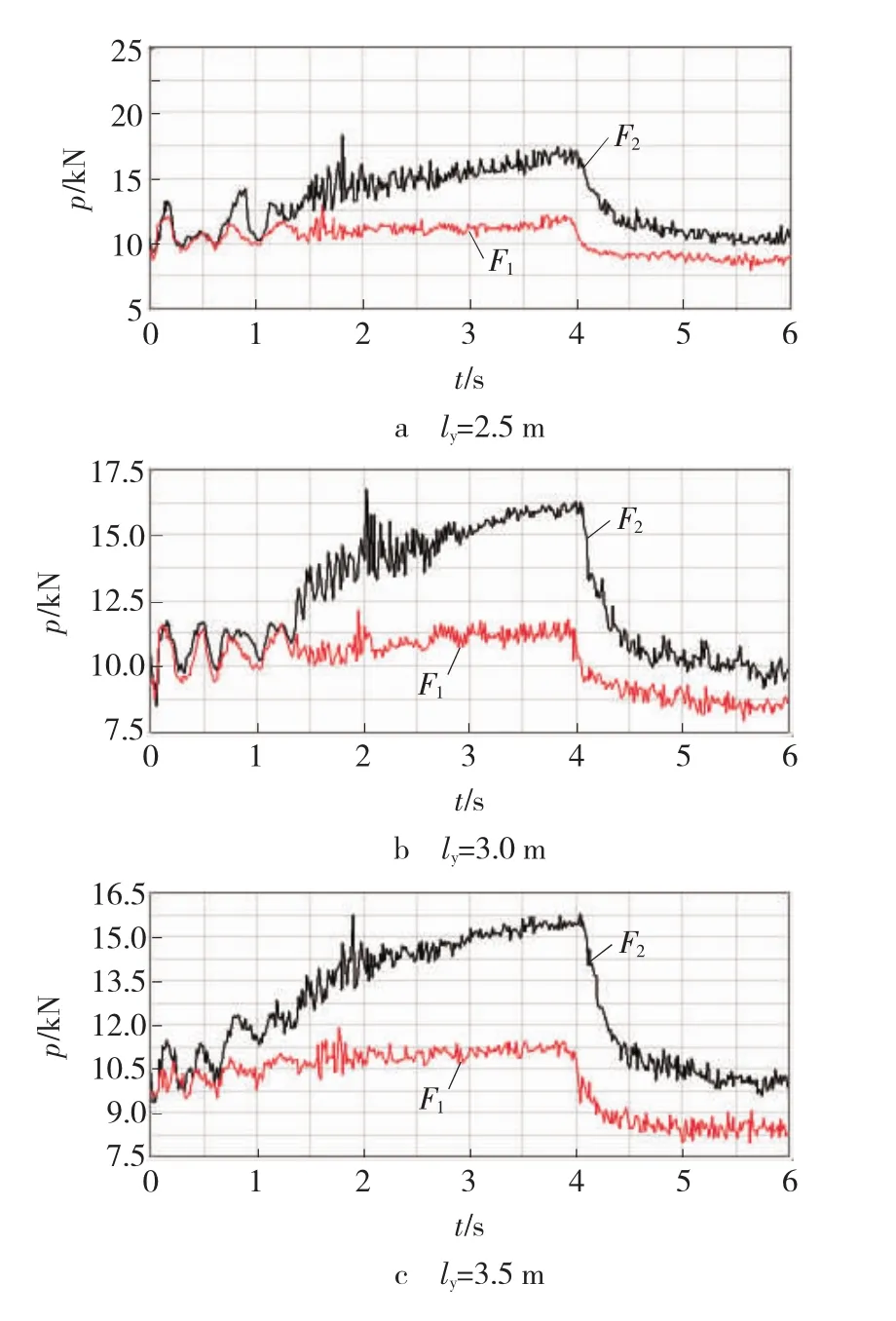
图2 不同压辊间距时的张力曲线Fig.2 Tensile force curve of different calender roll displacement
对于承载带上的测试点2,当压辊间距ly=2. 5 m时,张力在t =1. 8 s时达到最大值18. 2 kN;压辊间距ly= 3 m时,张力最大值为16. 7 kN;压辊间距ly=3. 5 m时,张力的最大值为15. 8 kN。从数据上看,随着压辊间距的增加,启动过程中测试点2处的最大张力值及其变化幅度减小,张力的波动性降低,说明最大张力值的变化与压辊间距的变化不成线性关系。同时,测试点1的最大张力值及其变化幅度小于测试点2。
2. 2.2 输送带刚度
图3 为运行速度v = 4 m/s时不同输送带刚度下张力的变化规律。曲线ceshidian1-Force.Mag ( F1)、ceshidian2-Force.Mag( F2)分别表示测试点1、2所在位置在运动过程中输送带的张力变化。由图3可见,覆盖带上的测试点1,在输送带刚度k = 1. 25×107N/m时,张力在t = 1. 9 s时达到最大值12. 1 kN;输送带刚度k =1. 25×106N/m时,张力在t =1. 9 s时达到最大值13. 3 kN;输送带刚度k = 1. 25×105N/m,张力在t = 1. 8 s时达到最大值15. 0 kN。故随着输送带刚度的降低,测试点1的最大张力值及其变化幅度均增加。
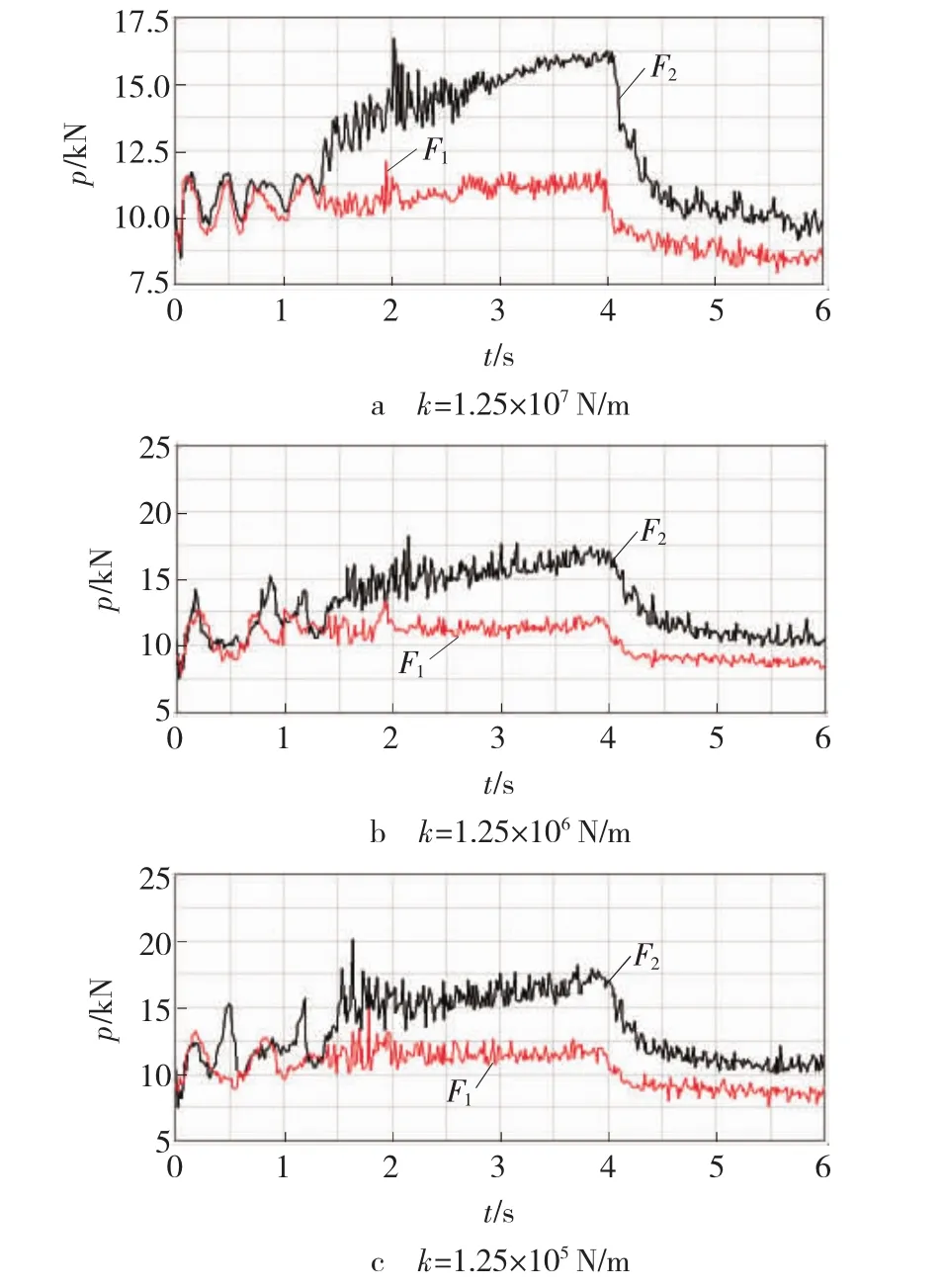
图3 不同刚度时的张力曲线Fig.3 Tensile force curve of different stiffness
承载带上的测试点2,在输送带刚度k =1. 25× 107N/m时,最大张力值为16. 7 kN;输送带刚度k = 1. 25×106N/m时,最大张力值为18. 2 kN;当输送带刚度k =1.25×105N/m时,最大张力值为20.1 kN。故随着输送带刚度的降低,测试点2的最大张力值及其变化幅度均增加。同时,测试点2的最大张力值及其变化幅度大于测试点1。
2. 2. 3 输送带阻尼
阻尼系数是影响输送带黏弹特性的重要因素之一,所以必须对不同阻尼系数下输送机的动态特性进行分析。图4为输送机运行速度v = 4 m/s时不同输送带阻尼系数时的张力曲线。曲线ceshidian1-Force.Mag( F1)、ceshidian2-Force.Mag( F2)分别表示测试点1、2所在位置的张力变化。对于覆盖带上的测试点1,当阻尼系数δ=1. 0×105Ns/m时,张力在t = 1. 9 s时达到最大值12. 1 kN;阻尼系数δ=1. 0×104Ns/m时,张力的最大值为13. 0 kN;阻尼系数c = 1. 0×103Ns/m时,张力的最大值为14. 3 kN。数据表明,随着输送带阻尼系数的降低,测试点1的最大张力值及其变化幅度增加。

图4 不同阻尼时的张力曲线Fig.4 Tensile force curve of different damping
对于承载带上的测试点2,当阻尼系数δ=1. 0× 105Ns/m时,张力在t =2. 0 s时达到最大值16. 7 kN;阻尼系数δ= 1. 0×104Ns/m时,张力的最大值为17. 9 kN;阻尼系数δ=1. 0×103Ns/m时,张力的最大值为19. 4 kN。数据表明,随着输送带阻尼系数的降低,测试点2的最大张力值及其变化幅度增加。同时,测试点2的最大张力值及其变化幅度大于测试点1。
数据表明,随着阻尼系数的降低,输送带运行过程中受到的阻力减小,削减振动的效果降低,导致输送带的振动加强,输送带的张力波动幅度增加。较大的阻尼系数在输送机的运行过程可以起到削弱振动强度的效果,所以实际应用中,应在满足要求的情况下尽量选取较大的阻尼系数,以减小整个输送机系统的振动。
2. 3输送带带速、输送量对输送机动态特性的影响
2. 3. 1 运行速度
图5 表示不同速度下的张力曲线,用曲线ceshidian1-Force.Mag( F1)、ceshidian2-Force.Mag ( F2)分别表示测试点1、2所在位置的张力变化。如图5所示,对于覆盖带上的测试点1,当速度v = 4 m/s时,张力在t =1. 9 s时达到最大值12. 1 kN;速度v = 5 m/s时,最大张力值为13. 0 kN;速度v = 6 m/s时,最大张力值为14. 5 kN。数据表明,随着带速的提高,测试点1的最大张力值及其变化幅度增加。

图5 不同速度时张力的曲线Fig.5 Tensile force curve of different velocity
对于承载带上的测试点2,当速度v =4 m/s,张力在t =2. 0 s时达到最大值16. 7 kN;速度v =5 m/s时,张力的最大值为17. 8 kN;速度v = 6 m/s时,张力的最大值为19. 6 kN。数据表明,随着带速的增加,测试点2的最大张力值及其变化幅度增加,并且测试点2的最大张力值及其变化幅度均大于测试点1。
由此表明,随着带速的增加,输送机系统的动态特性表现的越来越明显,运行过程中输送带及整个输送机系统的的振动加强,不稳定性增加,导致输送带(包括承载带和覆盖带)的张力增大,并且增大幅度更加明显。承载带上输送有物料,故其最大张力值及变化幅度要大于覆盖带。因此,要提高带速就必须改善输送机的动态性能,在张力增加幅度较小的范围内合理选择运行速度,以其提高运行速度且避免启动过程中的张力过大,提高输送机运行的稳定性与安全性。
2. 3. 2 输送量
图6 为输送机运行速度v = 4 m/s时不同输送量下输送带的张力曲线,ceshidian1-Force.Mag ( F1)、ceshidian2-Force.Mag( F2)曲线分别为测试点1、2所在位置处的张力变化。如图6所示,对于覆盖带上的测试点1,当输送量Q =200 t/h时,张力的最大值为12. 1 kN;输送量Q =400 t/h时,张力的最大值为12. 4 kN;输送量Q =600 t/h时,张力的最大值为12. 6 kN。数据表明,随着输送量的增加,测试点1的张力值略有增加,但变化较小。
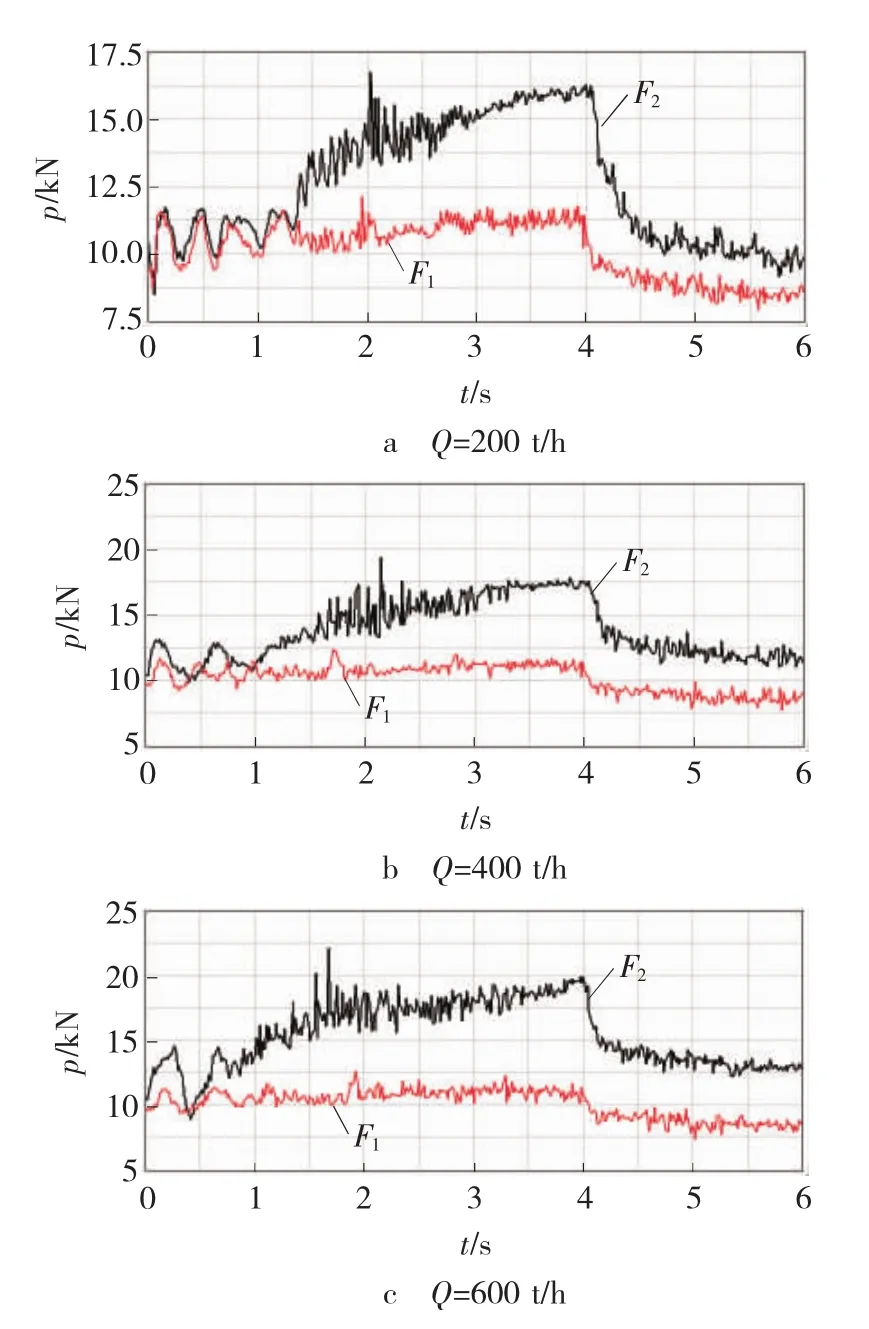
图6 不同输送量时的张力曲线Fig.6 Tensile force curve of different load
对于承载带上的测试点2,当输送量Q =200 t/h时,最大张力为16. 7 kN;输送量Q = 400 t/h时,张力最大值为19. 3 kN;输送量Q =600 t/h时,张力的最大值为22. 1 kN。数据表明,随着输送量的增加,测试点2的最大张力值增加,但增加的幅度比较稳定,说明最大张力值的变化与输送量的变化近似成线性关系,并且测试点2的最大张力值及其变化明显大于测试点1,说明由于输送量的增大,主要导致承载带张力增大。
数据分析表明,随着输送量的增加,启动过程中带式输送机的动态性能表现的越来越明显。输送机系统的振动加强,两输送带的速度波动变大,在物料的作用下,使得输送量的变化对承载带张力的影响更加明显,而对覆盖带张力的影响较小。承载带的最大张力值与输送量近似成线性关系,由此,根据已知输送量的张力曲线,估算某一未知输送量下的张力变化,以选择合理的安全系数。
3结论
( 1)随着压辊间距的增大,输送带的张力减小,且变化幅度降低。在保证夹持力的情况下,适当地加大压辊的间距,减少压辊数量,可以在一定程度上降低成本。
( 2)输送带的刚度与阻尼系数对输送带自身的黏弹特性有很大的影响。相同条件下,适当的增大输送带的刚度和阻尼系数,可以有效地减小启动过程中输送带的波动幅度。
( 3)在启动时间相同的条件下,随着带速的增加,输送带的张力波动范围加大,最大张力值增加,输送机系统的不稳定性增大。因此,在提高输送机运行速度时,应对输送机的动态特性进行分析,并采取合理的控制策略。
( 4)随着输送量的增加,启动过程中系统的不稳定性增加。因此,应在大运量时对输送带的动态特性进行分析。输送带的最大张力值与输送量近似成线性关系,据此可以通过已知输送量下的张力曲线,近似求得某未知输送量下的张力变化。
( 5)随着输送距离的增加,输送机系统的振动特性显著,输送带的黏弹特性也越来越明显。
[1] 杜月波.垂直带式输送机[J].建筑机械化,2000 ( 5) : 26-28.
[2] 周亚东.长距离矿用带式输送机启动过程的动态仿真研究[J].机械工程与自动化,2012( 1) : 31-35.
[3] 胡 坤,郭永存,王鹏彧,等.一种包含内摩擦的输送带动态特性研究[J].中国矿业大学学报,2012,41( 4) : 669-674.
[4]孙文涛.多点直线摩擦驱动带式输送机动态分析[D].哈尔滨:黑龙江科技学院,2012.
[5] 牛春水.基于虚拟样机技术的火电厂带式输送机动态特性分析[D].北京:华北电力大学,2012.
[6]葛正浩.ADAMS2007虚拟样机技术[M].北京:化学工业出版社,2010.
[7] 周广林,孙广涛.中间驱动装置对线摩擦带式输送机动态特性的影响[J].黑龙江科技学院学报,2012,22( 1) : 47-51.
[8]韩瑞飞.辊子压带式带式输送机的动态特性分析[D].黑龙江科技大学,2013.
(编辑 晁晓筠)
Dynamic characteristics analysis of roller sandwich belt conveyor
ZHOU Guanglin,HAN Ruifei
( School of Mechanical Engineering,Heilongjiang University of Science&Technology,Harbin 150022,China)
Aimed at improving the reliability and safety of the equipment operation,this paper is focused on using Pro/E to develop a model for the roller sandwich belt conveyor and analyzing the dynamic characteristics of the model under different conditions by ADAMS.The paper also discusses the law governing the effect of conveyor belt stiffness,damping coefficient,roller pressure distribution,belt speed and conveyor on the dynamic characteristics of the roller sandwich belt conveyor.The analysis suggests that the appropriate increase in the stiffness and damping coefficient of the belt results in an effective reduction in belt fluctuations due to start-up procedure; increased belt speed means an increase in the instability of conveyor system; there occurs an approximately linear relationship between the conveyor belt maximum tension value and the amount of the conveyor belt; there is a significant relationship between conveying distance and conveyor systems vibration characteristics; and an appropriate increase in the space of the press rollers enables a somewhat lower cost.It follows that the demonstrated feasibility of analyzing the dynamic characteristics of roller sandwich belt conveyor using virtual prototyped technology may serve as a theoretical basis for developing high-speed and long-distance roller sandwich belt conveyors.
belt conveyor; roller sandwich belt; dynamic characteristics;ADAMS
10. 3969/j.issn.2095-7262. 2014. 01. 019
TD528
2095-7262( 2014) 01-0085-06
A
