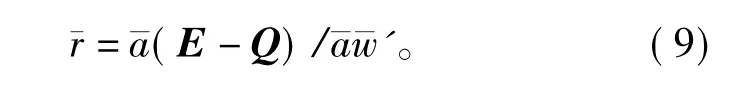马尔可夫链的离散人口预测模型及其应用
2014-11-08蔡吉花唐光平
蔡吉花,唐光平,姚 君
( 1.黑龙江科技大学理学院,哈尔滨150022; 2.湖南大学信息科学与工程学院,长沙410082)
马尔可夫链的离散人口预测模型及其应用
蔡吉花1,唐光平2,姚 君1
( 1.黑龙江科技大学理学院,哈尔滨150022; 2.湖南大学信息科学与工程学院,长沙410082)
为准确预测我国未来人口发展趋势,以我国近10年来人口数据为依据,对中国人口老龄化进程加快的问题进行统计分析。利用绝对分布的马尔可夫链人口预测模型,预测了未来中国人口结构,建立了基于模糊权马尔可夫链人口预测模型,对人口出生率和死亡率以及人口总数进行了预测,同时检验了这些预测模型的可靠性。最后讨论了基于平稳分布的人口结构控制问题。
人口结构;马尔可夫链;模糊权;人口预测
收稿日期: 2013-12-18
基金项目:黑龙江省教育厅科学技术研究项目( 12521479)
第一作者简介:蔡吉花( 1963-),女,黑龙江省尚志人,教授,硕士,研究方向:微分方程与随机过程,E-mail: caijh2003@163.com。
0引言
马尔可夫链模型是一种随机预测模型,与其他统计方法不同,它不需要从复杂的预测因子中寻求各因素之间的相互规律,只需考虑事件本身历史状况的演变特点,通过计算状态转移概率预测未来状态的变化趋势[1]。国内学者运用马尔可夫链模型对我国各地区的人均GDP的变化趋势及房价指数、人均旅游消费进行了预测分析。2011年,郭嗣琮等进一步对模糊马尔可夫链预测模型作了探讨。通过分析人口数据及历史状况的演变特点,马尔可夫链模型可以应用于建立离散人口预测模型。笔者利用我国近10年来人口数据,通过选取适当的状态变量,建立相应的离散人口模型,并用Matlab软件计算分析,修正模型,较准确预测了我国未来人口问题的发展趋势,分析了人口老龄化发展进程及控制问题。
1基于马尔科夫链的人口预测模型
1. 1绝对分布马尔科夫链预测模型
定义1[1]设{ X}是随机序列,状态空间E =
n{ 1,2,…,N},若P{ Xm + k=j Xm= i} = P(ijk)与m无关,称{ Xn}为时齐的Markov链。其中p(ijk)叫由状态i出发经k步到达状态j的转移概率。P( k)= ( p(ijk))N×N叫k步转移概率矩阵;当k =1时,P( 1)简记为P,P为一步转移概率pij所组成的矩阵,称为一步转移概率矩阵。k步转移概率矩阵由一步转移概率矩阵得到,即P( k)= Pk。
定义2 Markov链{ Xn}初始时刻各状态的概率P{ X0= i} = pi( i∈E),称为初始分布;在时刻n ( n≥0)取各状态的概率P{ Xn= i} = p(in)( i∈E),称为绝对分布,且
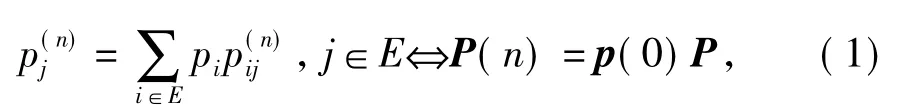
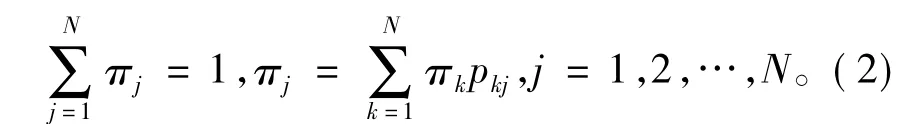
称π= (π1,π2,…,πN)为平稳分布,式( 2)也可写成矩阵形式:π=πP。
定理1对状态有限的马尔可夫链,如果存在k>0,使pij( k)>0,i,j =1,2,…,N,则此马尔可夫链是遍历性的[2]。
通过构造马尔可夫链的转移概率矩阵及初值分布,计算绝对分布及平稳分布,对未来各状态的结构进行预测的模型称为绝对分布马尔科夫链预测模型。
1. 2 人口生灭模型
定义4设齐次马尔可夫过程{ X( t),t≥0}的状态空间为E = { 0,1,2,…},转移概率为pij( t),如果则称{ X( t),t≥0}为生灭过程,λi为出生率,μi为死亡率。
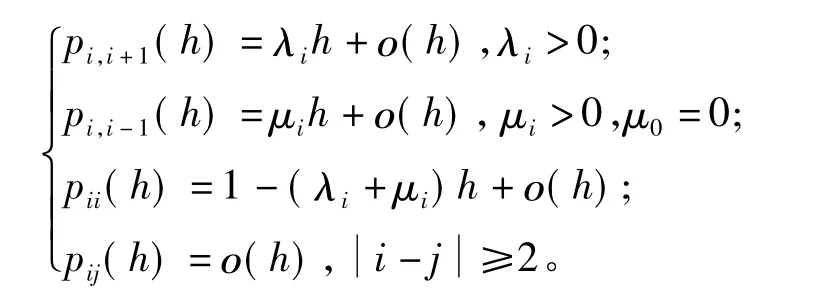
运用生灭过程建立的人口生灭模型可以简单地描述:
设λi为第i年的人口出生率,μi为第i年的人口死亡率,Si为第i年的人口数,S^i为第i年的预测人口数,用生灭链推导的人口数,有如下关系成立:

其中,λi和μi都不为0,式( 3)可用于中国人口总量的中长期预测。
1. 3模糊权马尔可夫链预测模型
模糊权马尔可夫链是改进的马尔可夫链模型,其基本求解步骤:
( 1)马尔可夫链的权重
首先计算指标样本序列的各阶自相关系数
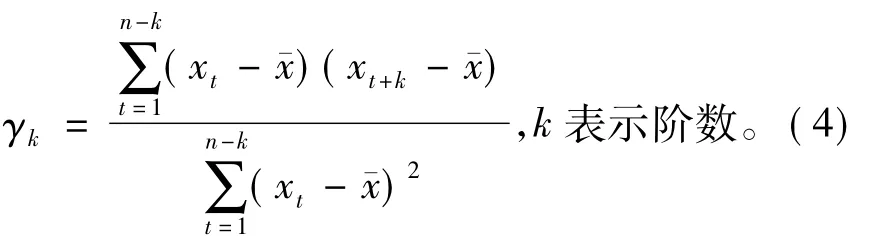
再将自相关系数规范化

并将其作为各阶马尔可夫链的权重( m为需要计算的时滞数)。
( 2)状态的划分
分五个步骤进行:
①选择统计指标和标定方法
设U = { u1,u2,…,un}为待分类的全体,ui表示第i个指标,用rij表示指标ui和uj的相似系数,0≤rij≤1 ( i,j =1,2,…,n)。rij计算常用绝对值减数法:
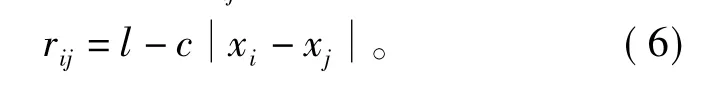
其中c适当选取,使rij在[0,1]中且尽量分散,记模糊矩阵R = ( rij)。
②模糊聚类
对模糊矩阵R,用逐次平方法求出其传递闭包珚R为模糊等价矩阵,再选择阀值λ,对U进行分类[3]。在选择一个阀值λ后,对传递闭包做如下处理:
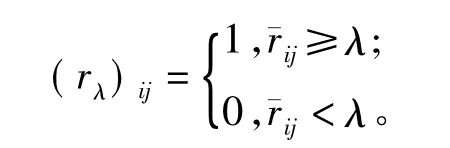
③状态划分
U的分类数就是马氏链的状态数,同时还得到各指标所对应的状态及具体划分范围。
④计算转移概率矩阵
根据各指标所对应状态进行统计,计算出一步以及多步转移概率矩阵。
⑤预测和检验
利用马尔可夫链权重ωk,结合k转移概率矩阵,预测某年处于状态i的概率值pi,
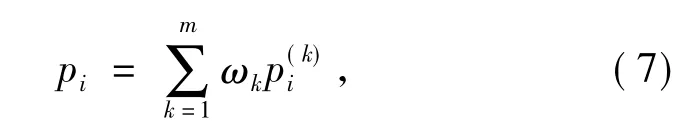
取max{ pi}的状态i作为某年预测状态[4]。通过对已知样本进行预测,检验预测的效果。
2 模型应用
将马尔可夫链的预测模型应用于中国人口指标的预测,包括人口结构、死亡率与出生率、人口总数预测及人口的控制。文中数据均来源于中国统计年鉴人口各项指标数据[5]。
2. 1绝对分布马氏链的人口结构预测
将人口按照0~14、15~34、35~49、50~64、65岁以上(对应于1~5状态)来划分,由2004~2009年各年龄段人口数据计算出各年龄段的人口所占比例,如表1所示。65岁及以上人口比例走势图如图1所示。
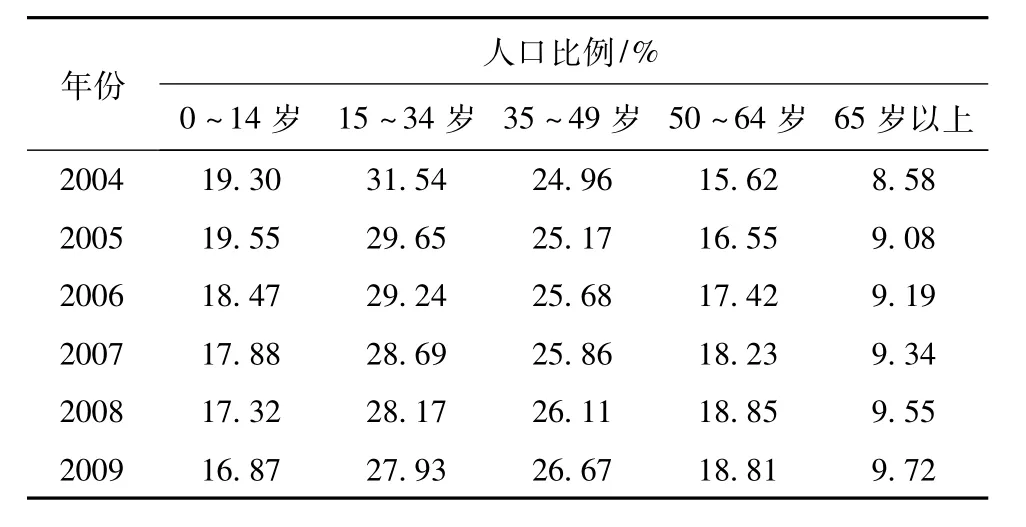
表1中国2004~2009年人口年龄结构数据Table 1 2004~2009 data of Chinese population age structure

图1 各年份65岁及以上人口所占比例Fig.1 Each year proportion of population for 65 years old and above 65
2.1.1转移概率矩阵
每相邻两年为一步,状态转移概率的计算方法如下[6]:
( 1)一步状态转移只会发生于其本身和相邻状态之间,且是状态i向状态j( j≥i)转移;
( 2)在相同状态i下,若n + 1年比n年的数据比例升高了,则记为pii= 1,而pij= 0,j = 1,2,…,5 ( j≠i) ;
( 3)在相同状态i下,若n + 1年比n年的数据比例下降了,则pii应该为n + 1年的比例与n年的比例的商值,而pi,i +1的值恰等于1-pii,pij= 0,j = 1,2,…,5( j≠i,i +1) ;
( 4)在n年到n +1年的过程中,若有状态i-1转移到状态i的数据发生,则计算状态i的转移概率时,应考虑加进状态i-1转移到状态i的数据部分,并加到计算比值的分母部分;
( 5)若状态5转移的部分不是全发生在本状态,且同年状态1的比例比前一年增加了,则记状态1增加的比例为状态5转移出的数据部分,依此类推。
按此转移概率计算方法,则2004~2005年的状态转移概率矩阵为

同样,计算2005~2006、2006~2007、2007~2008、2008~2009年的状态转移概率矩阵分别记为P2、P3、P4、P5。为了消除样本随机性影响,更好地描述状态规律,在此取P1、P2、P3、P4、P5的平均值作为状态转移概率矩阵P:

2.1.2遍历性与平稳分布
利用Matlab软件计算P14,其所有元素p(ij1
4)都大于0,该过程具有遍历性。
设{πj,j∈I}是该马尔可夫链的平稳分布,则由一步转移概率矩阵式( 8),可建立如下方程组,
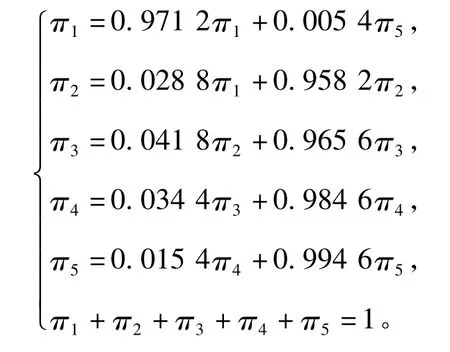
解上述方程组,得平稳分布:
π1=0. 102 8,π2=0.070 8,π3=0.086 0,π4=0.192 2,π5=0.548 2。
说明按照现行人口政策长此以往,中国人口的年龄结构比例中老年人口将达到54. 82%。
2.1.3人口年龄结构预测
采用2007~2009年这三年各年龄段所占比例的均值作为初始概率分布:
P( 0) = ( 17. 356 7 28. 263 3 26. 213 3 18. 630 0 9. 536 7)λ0。
利用式( 1)求绝对分布律,即把2009年作为初始年份,经过n年的人口结构分布记为
λn=λ0Pn。
2010~2012年的人口年龄构成进行预测:
λ2010=λ0P( 16. 908 3 27. 581 8 26. 493 0 19. 244 8 9. 772 1),
λ2011=λ0P2= ( 16. 474 1 26. 915 8 26. 734 5 19. 859 8 10. 015 7),
λ2012=λ0P3= ( 16.053 8 26.265 2 26.939 9 20.473 6 10.267 5)。
这个计算结果与2010、2011、2012年人口年龄构成实际值基本吻合。
同理,经过20年、30年、50年、100年的人口年龄构成如下:
λ20=λ0P20= ( 10.713 2 17.317 7 26.464 8 29.826 7 15.677 7),
λ30=λ0P30= ( 8.830 5 13.630 5 24.199 6 33.721 6 19.617 9),
λ50=λ0P50= ( 6.918 2 8.817 1 18.635 3 37.496 8 28.132 6)。
图2 可以直观地看出各年龄段人口比例变化趋势。从预测值分析得到,按照现行的人口政策,20、30年后,我国老年人口比例分别接近15%、20%; 50年后,老年人口比例占到近30%。我国人口老龄化进程在不断加快,这样必然造成社会抚养系数过大,不利于社会经济的持续发展。政府应适当调整人口政策,使人口结构趋向合理。
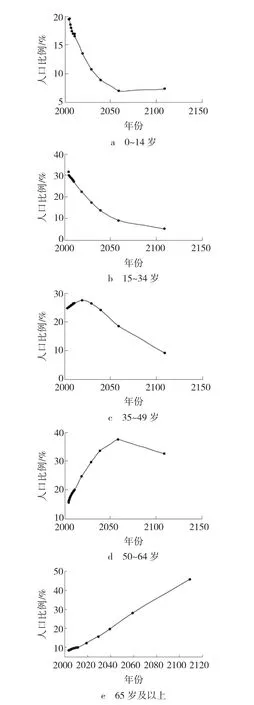
图2 2012~2112年各年龄段人口比例预测情况Fig.2 2012~2112 proportion of population forecast for all ages
2. 2模糊权马尔可夫链的人口死亡率与出生率预测
利用表2数据对人口死亡率作模糊权马尔可夫链的相关分析[7]。出生率预测方法类似得到。
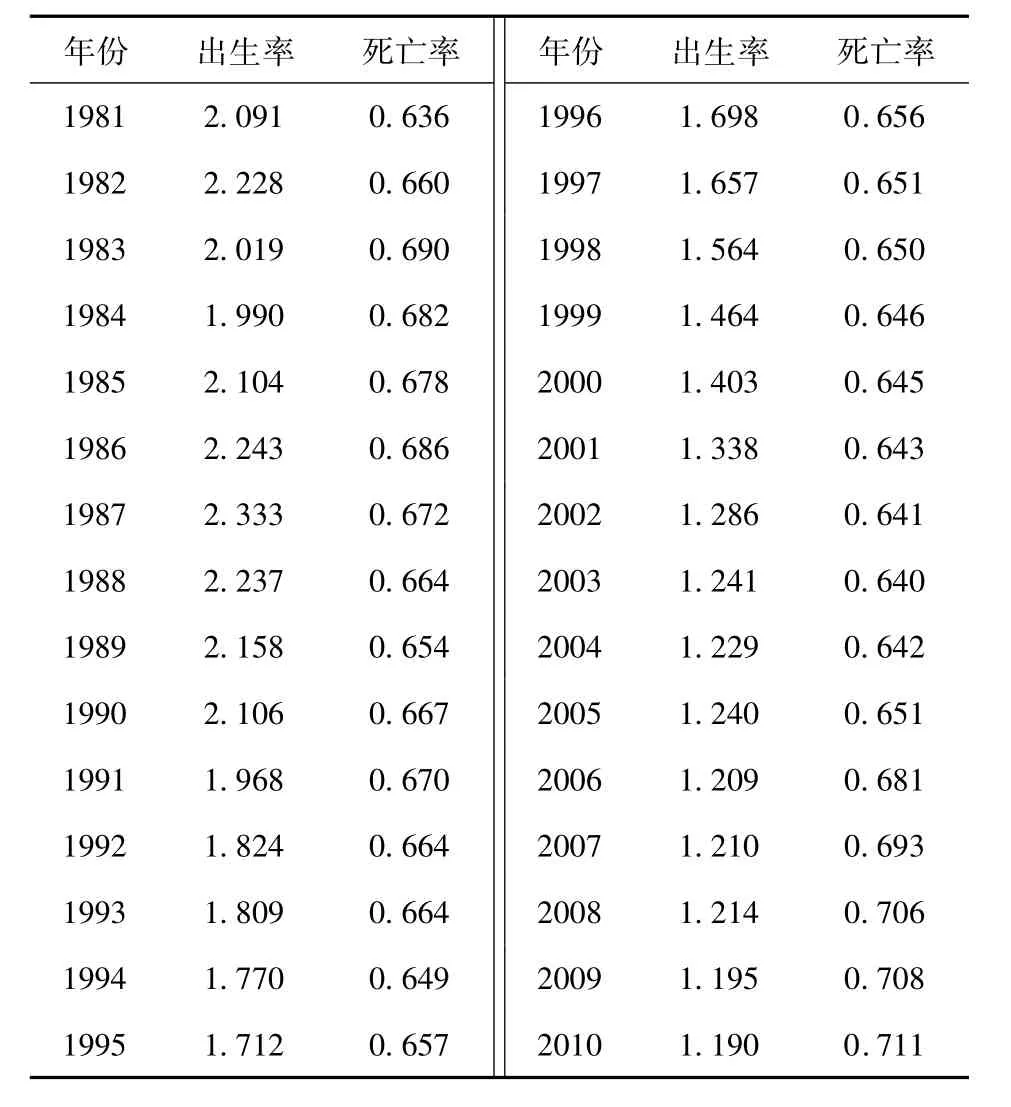
表2 1981~2010年人口出生率和死亡率Table 2 1981~2010 birth rate and mortality rate %
2.2.1人口死亡率预测
人口死亡率的基本求解步骤为:
( 1)马尔可夫链的权重
由表2和式( 4)求得人口死亡率序列的1~4阶自相关系数:
γ1=0.883 4,γ2=0.655 8,γ3=0.404 0,γ4=0.028 9。再由规范化式( 5)得到各阶马尔可夫链权重:
ω1=0.447 9,ω2=0.332 5,ω3=0.204 9,ω4=0.014 7。
( 2)模糊聚类
设U = { u1,u2,u3,…,u28,u29,u30}表示1981~2010年死亡率。由绝对值减数法( 6),取l = 1,c = 1.3,有rij=1-1.3× xi-xj,得到30阶模糊相似矩阵R = ( rij)30×30,再计算R的传递闭包珚R,得

选择阀值λ,求矩阵Rλ,并按Rλ将U分成若干个等价类。当λ= 0.80,将U分为一类;当λ= 0.92,将U分为两类,即{ u1,u2,u3,…,u25,u26,u27} 和{ u28,u29,u30} ;当λ= 0.94,U分为三类,即{ u1,u2,u7,u8,u9,u10,u11,u12,u13,u14,u15,u16,u17,u18,u19,u20,u21,u22,u23,u24,u25}、{ u3,u4,u5,u6,u26, u27}、{ u28,u29,u30} ;当λ= 0.96时,可将U分为七类。经计算分析后可以得到,当λ=0.94,将U分为三类时比较合理。
( 3)状态划分
U分为三类时对应的马尔可夫链取1、2、3三个状态,由表2的数据,可以划分各状态对应的死亡率区间分别为ui<0.675%、0.675%≤ui≤0.700%和ui>0.700%。
( 4)计算转移概率矩阵
根据各年份对应状态,求得死亡率的1步到4步转移概率矩阵

( 5)预测和检验
首先预测2011年的人口死亡率。由以上各步转移概率及式( 7),预测情况如表3。

表3 2011年死亡率的加权预测值Table 3 2011 weighted prediction of mortality rate
表3的最后一行是加权求和的结果,其中状态3的概率最大为0. 991 3,说明2011年人口死亡率状态等级为3,死亡率≥0.700%与2011年实际人口死亡率0.714%相符合。由这个预测值进一步预测2011年之后的死亡率情况表4,可以得到未来三年死亡率都在0.700%以上。
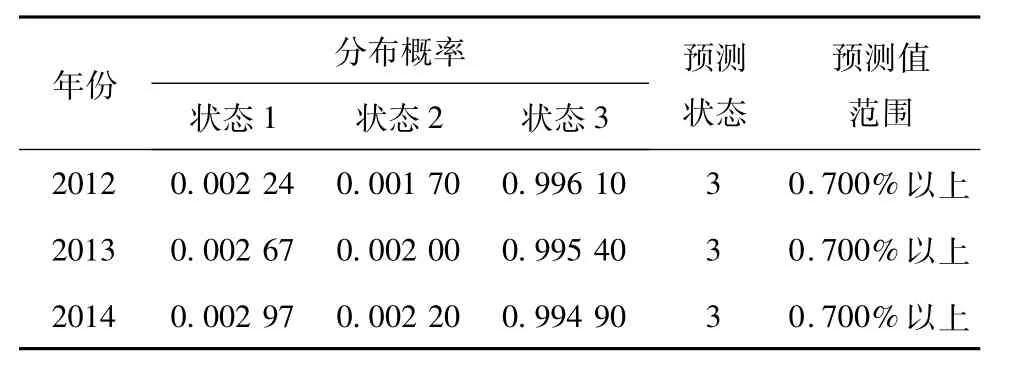
表4 2011年之后三年内死亡率预测值Table 4 Predictive value of mortality rate within three years after 2011
2.2.2人口出生率预测
类似死亡率预测方法,计算得到: ( 1)出生率的各阶马尔可夫链权重
ω1=0.266 7,ω2=0.254 6,ω3=0.245 1,ω4=0.233 6。
( 2)模糊聚类
记V = { v1,v2,v3,…,v28,v29,v30}表示1981~2010年人口出生率。利用rij= 1-0. 08× xixj,求得珚R = R16。经计算,当λ= 0. 94时,V分为五类,即{ v7}、{ v1,v2,v3,v4,v5,v6,v8,v9,v10,v11}、{ v12,v13,v14,v15,v16,v17}、{ v18}和{ v19,v20,…,v29,v30}。
( 3)状态的分类及转移概率矩阵
对应的马尔可夫链的五个状态记为1、2、3、4、5,根据表2得到各状态出生率对应区间分别为vi>2.250%、1.950% ( 4)预测和检验 利用出生率的各步状态转移概率矩阵及式( 7),预测2011、2012、2013、2014年的人口出生率均为≤1.500%,处于状态5,与2011、2012年人口出生率实际值相符。 2. 3生灭链的人口总数预测 运用人口生灭模型( 3) : S^i +1= Si( 1 +λi +1-μi +1),预测2010年和2011年人口总数为: S^ 2010=134 090万人,S^2011=134 730万人。而人口调查实际值为S2010= 134 091万人,S2011= 134 735万人,误差率分别为1. 323×10-5( 2010 年),1. 265×10-5( 2011年),预测效果较好。根据前面预测的2012、2013年死亡率μi≥0.700%,出生率λi≤1.500%相关数据[8],预测2012年、2013年人口总数值为: S^ 2012≤135 810万人,S^2013≤135 816万人。 按照此方法,可以继续预测2014年之后的人口数范围。利用预测的人口总数及结合2. 1中预测的人口结构比例,可得到相应各年龄段的人口数。 人口结构的自我控制是指既要抑制人口增长过快的趋势,又要使人口的年龄结构有一个合理的分布,使未来人口年龄结构珔a*更合理且稳定的增长趋势。从现在的人口结构出发[9],让各状态每年进入下一状态的人数在总进入人数中的比例珋r依赖于时间t年,希望从现在的人口结构出发,逐步调控珋r( t)尽快达到合理的人口结构珔a*。人口年龄结构的合理控制分析(不妨设人口状态为五个),得到控制方程 其中r珋 = ( r1,r2,…,r5),ri( i = 1,2,…,5)为每年进入第i状态的人数在总进入人数中的比例,ri≥0且为合理的年龄结构; E为单位矩阵; Q = ( qij)为准转移阵( qij表示每年从i级转到j级人数在i级总人数中的百分比) ; w珔 = ( w1,w2,…,w5),wi为每年从第i级退出的比例,于是 。由于要求ri≥0,所以a珔( EQ)中的每一项即,因此对于珔a∈,j∈I},由式( 9)找到r珋,可见合理的稳定分布必须在集合A中。 取理想的人口结构珔a = ( 0. 18,0. 24,0. 26,0. 24,0. 08),由表1和表2数据及式( 9)计算得到: 珋r = ( 0. 236 8,0. 236 3,0. 228 2,0. 196 8,0. 083 3)。这表明目前我国应适当加大生育比例,使0~14岁的人口比例要逐步增加到23. 6%。为使人口结构能够维持一个合理的稳定水平,先从控制珋r = ( r1,r2,…,r5)开始。2013年国家出台生育二胎的政策会使未来中国人口结构更趋于合理。 [1]孙荣恒.随机过程及其应用[M].北京:清华大学出版社,2004: 74-76. [2]刘次华.随机过程[M].4版.武汉:华中科技大学出版社,2008: 89-92. [3]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004: 68-73. [4] 徐 娟,康 宁,张希娜.权马尔可夫链在人口死亡率时序误差预测中的应用[J].数学理论与应用,2008,28 ( 1) : 121-125. [5]中华人民共和国国家统计局.中国统计年鉴[M].北京:中国统计出版社,2004~2011. [6] 张 雯,靳军会,翟 彬.Markov链在中国人口年龄结构预测中的应用[J].河南商业高等专科学校学报,2008,21( 4) : 45-48. [7] 张 宸,林启太.模糊马尔可夫链状模型及其工程应用[J].武汉理工大学学报,2004,26( 11) : 63-66. [8] 卞焕清,夏乐天.基于灰色马尔可夫链模型的人口预测[J].数学的实践与认识,2012,42( 7) : 89-94. [9] 蒋远营,王 想.人口发展方程模型在我国人口预测中的应用[J].统计与决策,2011,15( 339) : 52-56. [10]彭志捌.AR( p)模型在中国总人口预测中的应用[J].河北工程大学学报:自然科学版,2007,24( 4) : 109-112. (编辑 晁晓筠) Markov chain-based discrete population prediction model and its application CAI Jihua1,TANG Guangping2,YAO Jun1 ( 1.School of Sciences,Heilongjiang University of Science&Technology,Harbin 150022,China; 2.School of Information Science&Engineering,Hunan University,Changsha 410082,China) Aimed at accurately predicting future demographic trends in China,this paper draws on population data in recent 10 years in our country and presents a statistical analysis of the accelerating process of China’s aging population,and a prediction of the future structure of China’s population using the population prediction model based on the absolute distribution Markov chain.And coupled with these is the development of a population projection model based on Fuzzy weighted Markov chain,the birth and death rates,on which to predict the total population and test the reliability of these prediction models.The paper ends with the discussion of the demographic control problem based on stationary distribution. population structure; Markov chain; Fuzzy weights;population forecast 10. 3969/j.issn.2095-7262. 2014. 01. 024 O211. 6 2095-7262( 2014) 01-0108-07 A3基于理想人口结构的人口控制