水平定向钻进铺管地表工后沉降分析
2014-11-08石朋飞
石朋飞,泮 伟,周 林
(1.中交第二公路勘察设计研究院有限公司,湖北 武汉430056;2.湖北水利水电职业技术学院,湖北 武汉430070)
水平定向钻进铺管技术由于具有对环境污染、交通影响、地层破坏较小,且施工周期短、成本低、社会和经济效益显著等优点,目前已广泛应用于市政给排水、天然气、煤气、通讯、电力等领域的管线建设中[1]。根据水平定向钻进铺管的施工工艺特点,该技术不可避免地会导致地表产生沉降变形,且变形主要产生在铺管完成以后阶段,即地表工后沉降[2—3]。本文基于随机介质理论,对水平定向钻进铺管导致的地表工后沉降问题进行了分析,建立了非均匀收敛的地表工后沉降理论计算模型,并利用MATLAB强大的数据计算和图像处理功能,基于MATLAB GUI编写了相应的程序计算软件,可定量地分析评价水平定向钻进铺管引起的地表工后沉降变形程度,可为水平定向钻进铺管工程施工和设计提供指导,具有很强的工程实用价值。
1 基于随机介质理论的水平定向钻进地表工后沉降模型
1.1 随机介质理论
波兰学者李特威尼申(Litwiniszyn)在研究采煤岩层与地表移动问题时提出了随机介质理论,他认为土粒、砂粒、破碎矿岩、岩块体等都属于随机介质范畴。自随机介质理论被提出后,先后经过很多学者的研究完善,特别是经我国学者刘宝琛和廖国华等的研究发展,其应用领域已经从最开始的预测煤矿地下开采引起的地表移动变形问题,发展到近地表地下工程开挖、边坡和基坑开挖等引起的地表变形预测等[4]。在近地表工程开挖问题研究中,对开挖引起的单个岩土体颗粒运动情况进行分析是难以实现的,但大量的研究结果表明,总的岩土体运动趋势具有明显的规律性,对其进行分析可行性较强[5]。根据随机介质理论,水平定向钻孔钻进的岩土体可视为随机介质,因而钻孔施工所引起的地表沉降变形适宜采用随机介质理论进行分析。
1.2 水平定向钻进地表工后沉降模型的建立
如图1所示,设水平定向钻进钻孔开挖断面深度为H,开挖初始断面为Ω,对于地表采用坐标系xoz,对于开挖单元土体采用坐标系ξoη。依据统计学的观点,可以将整个钻孔开挖分解成无限多个小单元开挖,则整个开挖对地表造成的影响就等于构成这一开挖的无限多个小单元开挖影响的总和。如果钻孔开挖断面全部发生坍塌,则上覆地层经过长时间移动变形后,在单元开挖dξdη的影响下,引起距离开挖单元中心x的地表点的最大下沉值We(x)为[6]

式中:r(η)为开挖单元在z方向上的主要影响半径(cm),r(η)=η/tanβ;β为上覆土体的主要影响角(°),其值取决于开挖所处的土层条件[7],可根据地质勘测资料选取。

图1 水平定向钻孔开挖示意图Fig.1 Excavation diagram of horizontal directional drilling
应用叠加原理,则整个开挖范围Ω完全坍塌导致的该点地表下沉值为

实际上,水平定向钻进铺管完成以后钻孔断面不会全部坍塌,其坍塌的范围是钻孔和铺设管道之间的间隙。如图2所示,当管道铺设完成后,铺设的管道与钻孔不是同心的,而是下沉到钻孔底部,最终的钻孔断面由Ω非均匀收缩为ω,则由叠加原理可知,地下钻孔开挖所引起的地表最终下沉值应等于开挖范围Ω与开挖范围ω两者引起的地表最终下沉值的差值,即

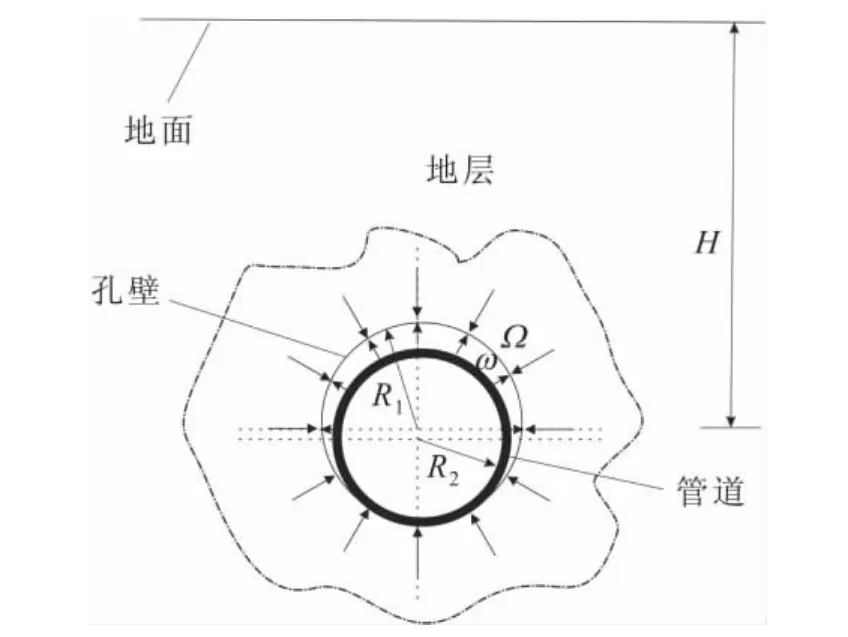
图2 水平定向钻进铺管断面示意图Fig.2 Cross-section diagram of horizontal directional drilling
设钻孔半径为R1,管道半径为R2,则铺管施工完成后引起的地表最终沉降值计算公式为

其中:

对该理论模型进行求解涉及到复杂的数学计算,为了便于计算分析,编写了基于MATLAB GUI的计算程序界面[8],如图3所示。

图3 水平定向钻进铺管地表工后沉降计算程序Fig.3 Calculation program of surface settlement caused by horizontal directional drilling after pipeline construction
2 沿水平定向钻孔轨迹地表工后沉降分析
水平定向钻孔轨迹一般是由造斜段和直线段构成的,其具体的轨迹形式有多种,但是无论哪种轨迹形式,沿钻孔轨迹方向各点的埋深不是一成不变的,且入土端和出土端的埋深较浅。图4为某水平定向钻进铺管工程的钻孔轨迹,水平距离全长100m,入土角为-15°,出土角为15°,最后一级扩孔直径为1 000mm,铺设管道的直径为820mm。根据此水平定向钻进铺管工程的钻孔轨迹,利用建立的理论计算模型,计算分析了沿水平定向钻孔轨迹方向地表工后沉降的分布形态和规律,其结果见图5和图6。

图4 某水平定向钻进铺管工程的钻孔轨迹Fig.4 Drilling trajectory of horizontal directional drilling in pipeline construction engineering
由图5和图6可以直观地查看沿钻孔轨迹一定范围内的地表各点的工后沉降值和沉降等值线分布,通过分析得出:
(1)沿钻孔轨迹横断面上,钻孔轴线正上方地表工后沉降值最大,随着距钻孔轴线水平距离的增加,地表工后沉降值逐渐减小,沉降等值线分布也逐渐变疏。
(2)沿钻孔轨迹纵断面上,入土端和出土端由于钻孔埋深浅,地表工后沉降值较大,且沉降等值线分布密,随着钻孔埋深的增加,地表工后沉降值逐渐减小,沉降等值线分布逐渐变疏。
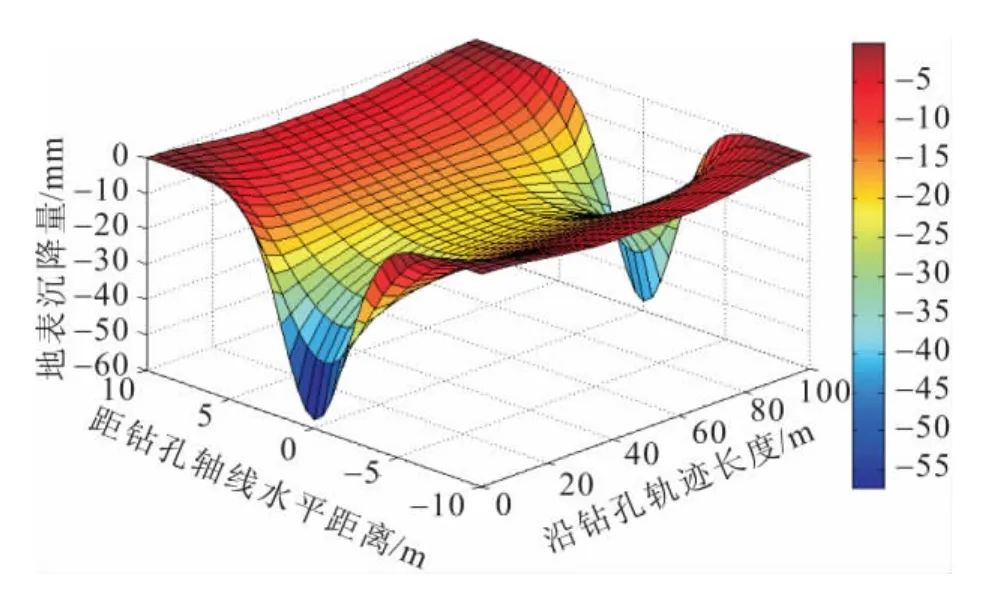
图5 沿钻孔轨迹地表工后沉降分布图Fig.5 Surface settlement distribution along the drilling trajectory after pipeline construction

图6 沿钻孔轨迹地表工后沉降等值线分布图Fig.6 Surface settlement contours along the drilling trajectory after pipeline construction
3 工程实例分析
上海某电力管道工程采用水平定向钻进铺设2根φ180MPP管道,长度为110m。施工段地质条件较为简单,表层为人工回填土,随着深度的增加地层分布依次为粉质黏土、淤泥质粉质黏土和淤泥质黏土,铺管穿越地层主要在粉质黏土和淤泥质粉质黏土中进行。水平定向钻进铺管入土角为-18°,出土角为18°,管线最大埋深为5.9m,最终扩孔直径为φ400,在导向孔施工完成后,采用φ400回扩器反拉旋转一次扩孔成形。现场使用Vermeer-D33×44水平导向钻机,其最大回拖力为25t。
为了监测铺管完成后的地表沉降,在管线上方地表处设置了沉降监测点(见图7),并使用DS03型水准仪对地表工后沉降进行现场监测,测量精度为0.01mm。具体监测点的布置情况见表1。

图7 地表沉降监测点平面布置图Fig.7 Floor plan of surface settlement monitoring points

表1 地表沉降监测点布置情况Table 1 Arrangement of surface settlement monitoring points
取铺管完成后不同监测点10d、30d、60d和90d的地表工后沉降实测数据绘图,其结果见图8。把监测点A、B、C所在断面定义为横断面1,把D、E、F和G、H、I所在断面分别定义为横断面2和横断面3,取90d的地表工后沉降实测值与理论计算的最大工后沉降值进行对比,其结果见图9。
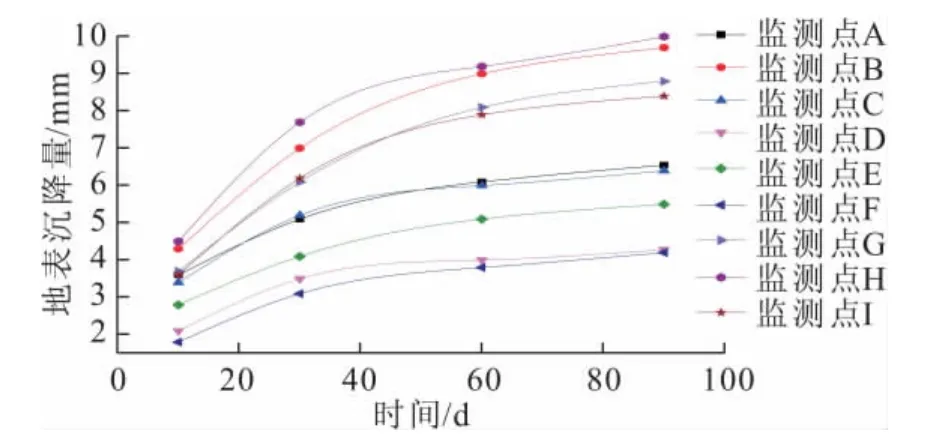
图8 不同监测点地表工后沉降实测曲线Fig.8 Measured data of surface settlement
由图8和图9可以看出:铺管完成10d后地表工后沉降值已经达到理论计算的最大工后沉降值的50%左右,随着时间的发展,沉降速度逐渐变小;铺管完成后90d时地表工后沉降值已经达到了理论计算的最大工后沉降值的90%左右,且沉降已趋于稳定;埋深浅时横断面地表工后沉降曲线趋势较陡,埋深大时其沉降曲线趋势较缓。

图9 横断面地表工后沉降实测值与理论计算的最大工后沉降值的对比曲线Fig.9 Contrast of measured settlement with theoretical value
4 结 论
本文基于随机介质理论,建立了适用于分析计算水平定向钻进铺管地表工后沉降的非均匀收敛理论模型,并编写了相应的计算程序,通过实例计算分析,得出以下结论:
(1)钻孔轴线正上方地表工后沉降值最大,随着距钻孔轴线水平距离的增加地表工后沉降值逐渐减小;入土端和出土端钻孔埋深小,地表工后沉降值较大,沉降等值线分布密,随着钻孔埋深的增加,地表工后沉降值变小,沉降等值线分布变疏。
(2)铺管完成初期地表工后沉降发展较快,随着时间的增加,地表工后沉降发展速度逐渐变缓,铺管完成90d时地表工后沉降已趋于稳定,其值为理论计算值的90%左右。
(3)水平定向钻进铺管入土端和出土端地表工后沉降变形较大,若超出地表工后沉降变形控制标准,则需要采取有效控制措施。
[1]乌效鸣,胡郁乐,李粮纲,等.导向钻进非开挖铺管技术[M].武汉:中国地质大学出版社,2004.
[2]李俊.水平定向钻铺管工程潜在安全隐患及对策研究[D].北京:中国地质大学(北京),2011.
[3]刘大金.土体中水平钻孔孔壁稳定性分析及试验研究[D].长春:吉林大学,2006.
[4]阳军生,刘宝琛.城市隧道施工引起的地表移动及变形[M].北京:中国铁道出版社,2002.
[5]高盼,郭广礼.基于随机介质模型的隧道施工地表沉降预计[J].金属矿山,2010(9):166-169.
[6]黎新亮.浅埋暗挖隧道地层变位随机介质理论分析及控制技术研究[D].北京:北京交通大学,2008.
[7]袁杰.地铁隧道开挖诱发的地表沉降与变形预测分析[D].北京:北京交通大学,2010.
[8]罗华飞.MATLAB GUI设计学习手记[M].北京:北京航空航天大学出版社,2009.
