基于粒子群优化的WA-SVM 模型在滑坡位移预测中的应用
2014-12-05吴北平陈美华李前云
杨 虎,吴北平,陈美华,李前云
(1.海南水文地质工程地质勘察院,海南 海口 570100;2.中国地质大学信息工程学院,湖北 武汉 430074;3.湖南有色测绘院,湖南 长沙 410129;4.重庆市208水文地质工程地质队,重庆 400700)
我国滑坡灾害非常严重,加强对典型滑坡体的地质调查、监测和治理,对可能发生的滑坡进行预测,具有重大的经济和社会意义[1]。滑坡体受到岩土类型、地形地貌、气候及人类活动等因素的影响,是一个复杂的非线性系统,目前仅用物理方法或数学方法还难以对滑坡进行完全描述,需要借助数理统计及其他一些不确定方法来加以描述,以弥补物理方法等存在的不足。目前各种借助于时间序列分析的方法在揭示滑坡位移时间序列规律中起着很重要的作用,其中混沌分析法在滑坡位移序列中获得了较广泛的应用,如李端有等[2]通过对滑坡位移序列进行混沌识别,结果表明滑坡位移序列中存在混沌特性。而基于嵌入定理和相空间重构理论可以从单变量的滑坡位移序列中恢复其原动力学系统,并在此基础上建模预测,常用的混沌预测模型主要有灰色模型[3]、最大Lyapunov指数模型[4]、人工神经网络模型[5]、支持向量机模型[6]等。
小波分析(Wavelet Analysis,WA)具有较好的时频局部化特点,能提取出滑坡位移序列的趋势性、周期性和随机性等多时间尺度的信息,对具有混沌特性的滑坡位移序列可起到平滑消噪的作用,近来也用于滑坡位移预测的研究中,其物理实质就是在重构相空间时,混沌吸引子向小波滤波器向量所张的空间中投影,与F.Takens提出的相空间重构理论在本质上是一致的[7]。支持向量机(SVM)采用结构风险最小化原则,能有效解决小样本、非线性等回归问题,具有较强的泛化能力[8]。宋星原等[9]将WA-SVM 耦合模型用于流域月降水预测研究,获得了较好的预测效果。然而,SVM 模型预测性能在很大程度上依赖于其参数的选择,而SVM 模型参数选取均采用穷举法等人工反复试算的方法,不仅效率低且得到的未必是全局最优解[6,10]。针对这一问题,可采用具有全局最优搜索能力且实现简单的粒子群优化(PSO)算法选取SVM 模型参数。为此,本文结合WA 能降低噪声影响、SVM 模型预测精度高以及PSO 算法参数寻优能力强的优点,提出了基于粒子群优化的小波分析-支持向量机的滑坡位移预测模型(即WA-SVM 模型),并将该模型应用于滑坡位移序列实例中,以期为滑坡位移预测研究探索出一种新的方法。
1 滑坡位移序列相空间重构和混沌识别
滑坡是一种既普遍存在又极其复杂的现象,它不是通常概念下确定性运动的三种定常状态:静止、周期运动和准周期运动,而是一种始终限于有限区域且轨道永不重复、性质复杂的运动。从滑坡系统的运动轨迹也可以看出,滑坡位移序列既表现出了一定的规律性,又表现出随机性,可能具有混沌特性。
传统的低维坐标系无法揭示混沌系统的复杂动力学特征,所以需要结合混沌理论中的相空间重构技术。Tanks嵌入定理认为,对于决定性系统长期演化的任一变量的时间演化过程,均包含了系统所有变量长期演化的全部信息。重构系统的相空间只需考察滑坡影响因素中的一个分量,通过某些固定的延时点上的观测值找到该相空间的m 维向量,就可以重构出一个和滑坡原系统等价的相空间。因此,可以通过单一的滑坡位移序列去建立恰当的模型来研究滑坡的动态演化特征。周创兵等[11]对长江新滩滑坡监测位移时间序列进行混沌特性分析,并结合相空间重构技术,重新建立滑坡动态演化特征并进行预测,取得了较理想的预测精度。
确定延迟时间和嵌入维是重构相空间的关键,目前确定延迟时间和嵌入维的常用方法分别为自相关函数法和伪最近邻点法等[12]。设滑坡位移序列为{xi,i=1,2,…,n},选取适当的延迟时间τ 和嵌入维数m,可以将其重构成一个m 维的相空间:
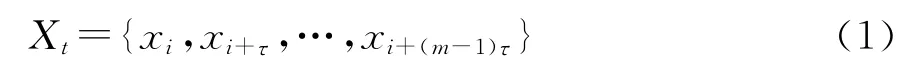
式中:Xt为m 维相空间中的相点;t=1,2,…,n-(m-1)τ。
在相空间重构的基础上,可对滑坡位移序列进行混沌特征识别,常用的定量识别方法是通过计算混沌信号奇异吸引子的特性参数,而描述邻近轨道发散率的最大Lyapunov指数可以表征系统的演变特性[4],当最大Lyapunov指数大于0时,表明系统存在混沌特征。本文使用小数据量方法计算滑坡位移序列的最大Lyapunov指数。
2 粒子群优化的WA-SVM 模型基本原理
2.1 小波分析(WA)
小波分析是对信号的一种时间-频率分析手段,在时域、频域上均有优良的局部化、多分辨率分析的特点,它可以对信号进行伸缩平移运算,从而实现了对信号多尺度细化。其基本思想是:对于原始序列s,经小波分析可分解为高频分量d1和低频分量a1,然后将低频分量进一步分解,如此重复可以得到任意尺度上的高频部分和低频部分。
通过对滑坡位移序列进行小波分析,可以将其趋势特征、周期特征和随机特征提取出来,然后分别对不同特征量进行预测,从而达到降低噪音影响的目的。
2.2 支持向量机(SVM)
支持向量机是一种建立在统计学理论和结构风险最小化原理基础上的机器学习方法,其基本思想是:通过一个非线性映射函数φ,将输入空间的数据集映射到高维特征空间G 上进行线性回归,在高维空间上只需进行内积运算,而这种内积运算可用原空间中的函数实现,从而很巧妙地解决了φ 未知的问题。实现高维空间内积运算且符合Mercer条件的对称函数称为核函数;此外对支持向量机预测能力影响较大的还有支持向量机的参数,这些参数主要包括核函数参数g 和惩罚系数C。
2.3 粒子群优化(PSO)算法
粒子群优化算法是由J.Kennedy等[13]提出的基于群智能寻优的演化计算技术,通过群体中各粒子之间的竞争和合作形成的群体智能来优化搜索。其数学描述为:初始化D 维向量空间中K 个随机粒子,其中第k 个粒子的位置向量为yk=(yk1,yk2,…,ykD),速度向量为vk=(vk1,vk2,…,vkD),(k=1,2,…,K),将yk代入目标函数,计算出每个粒子的适应度值,确定每个粒子的当前个体最优解pbest记为Pk=(pk1,pk2,…,pkD)和当前群体最优解gbest记为Pg=(pg1,pg2,…,pgD),其中Pk为在某次迭代时单个粒子经历过的最好位置,Pg为在某次迭代时群体中所有粒子经历过的最好位置。在每一次迭代中,找到Pk和Pg这两个最优解之后,就可以根据下面公式更新粒子的速度向量和位置向量:

式中:t=1,2,…,Tmax代表迭代次数;ω 为惯性权重;r1和r2为区间[0,1]上的随机数;c1和c2为学习因子。
3 基于粒子群优化的WA-SVM 模型的建模过程
基于粒子群优化的WA-SVM 模型的建模过程(见图1)如下:
(1)将滑坡位移序列{xi,i=1,2,…,n}归一化到区间[-1,1],确定延迟时间τ 和嵌入维数m 并对其重构相空间,然后对其进行混沌特性识别。
(2)使用小波分析对滑坡位移序列进行分解,得到低频分量aJ和高频分量dj(j=1,2,…,J,为分解的尺度数),然后分别对各分量重构相空间。
(3)分别对各分量采用粒子群优化的SVM 模型进行建模预测,最后将预测结果合成得到最终预测值。
(4)为了评定模型的有效性,选用平均相对误差绝对值MAPE和均方根误差RMSE 作为性能评价指标,其计算式如下:

式 中:xi为实测 值;^xi为预测 值。

图1 粒子群优化的WA-SVM 模型建模过程示意图Fig.1 Modeling progress diagram of WA-SVM model based on PSO
4 实例分析
4.1 数据来源
硝洞槽-郑家大沟滑坡位于巫溪县中梁乡中梁水库南岸,本实例数据采用硝洞槽-郑家大沟滑坡12号监测点位移监测资料,时间序列的间隔为2d,长度为134期,取后15期作为验证预测效果的样本集,该滑坡监测点原始时间序列见图2。
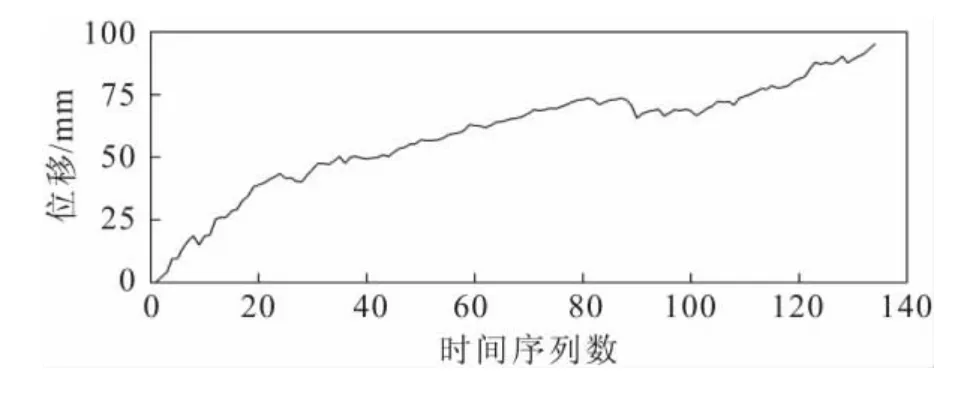
图2 硝洞槽-郑家大沟滑坡监测点原始时间序列Fig.2 Original time series of the displacement monitoring point of Xiaodongcao-Zhengjiadagou landslide
4.2 相空间重构
对硝洞槽-郑家大沟滑坡位移序列进行相空间重构,计算得到延迟时间τ为1,嵌入维数m 为4,且该滑坡位移序列最大 Lyapunov 指数值为0.017 3>0,证明该滑坡位移序列具有混沌特性,同时也表明在对滑坡位移序列进行相空间重构的基础上,将基于粒子群算法的WA-SVM 模型用于滑坡位移预测是切实可行的。
4.3 小波分解
对归一化后的滑坡位移序列使用Mallat算法进行小波分解。对于小波分解的层数,经过反复试验,发现分解到3 层即可得到较好的效果,故采用db6小波函数将滑坡位移序列分解为3层,得到低频分量a3和各尺度高频分量d3、d2、d1,见图3。

图3 小波分解后各个分量序列Fig.3 Component series after wavelet decomposition
4.4 PSO 算法选取SVM 模型参数
4.4.1 参数选取过程
分别对小波分解后的各个频率分量进行相空间重构,由上面计算得到延迟时间τ=1,采用预测误差最小原则确定各分量a3和d3、d2、d1的最佳嵌入维数m 分别为3、4、4、5,再用PSO-SVM 模型对各分量进行预测。SVM 模型均采用高斯径向基核函数,需要选取的参数主要包括核函数参数g 和惩罚系数C。采用PSO 算法选取SVM 模型参数的具体步骤如下:
(1)初始化粒子群,每个粒子的位置向量对应着一组参数(g,C),选定随机粒子总数K、学习因子c1和c2、最大迭代次数Tmax、核函数参数g 范围和惩罚系数C 范围,惯性权重ω 采用线性递减方式进行调整。表1为PSO 算法设定的初始参数值。

表1 PSO 算法设定的初始参数值Table 1 Initial parameter values of PSO
(2)根据适应度函数计算每个粒子的适应度值,比较每个粒子的适应度值和自身最优值pbest,将较好者作为当前个体最优值pbest;同理更新群体最优值gbest。适应度函数为

式中:zk和分别表示第k 个粒子的预测值和实测值。
(3)根据式(2)和式(3)更新粒子的位置向量和速度向量,判断是否满足条件:若搜索到的群体最优位置小于预定最小适应阈值ε或迭代次数达到预定的最大迭代次数,如果满足,终止迭代;如果不满足,则返回步骤(2)。
4.4.2 参数选取结果
粒子群优化算法对SVM 模型进行参数寻优的结果如图4至图7所示,图中进化代数表示粒子群进化所迭代的次数,最终求得的各分量参数值见表2。

图4 基于PSO 的SVM 模型a3分量的参数选取Fig.4 Parameter selection of a3component in SVM model based on PSO
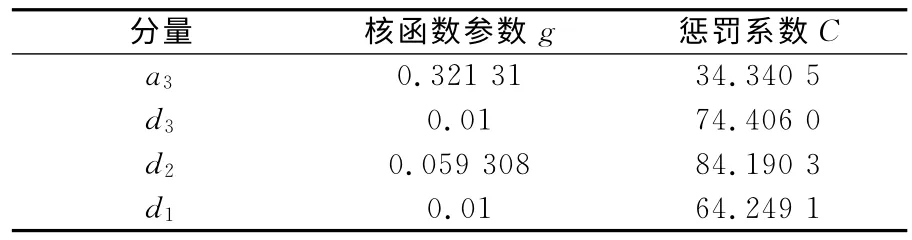
表2 各分量参数的选取结果Table 2 Parameters for each components
4.5 WA-SVM 模型预测结果

图6 基于PSO 的SVM 模型d2分量的参数选取Fig.6 Parameter selection of d2component in SVM model based on PSO
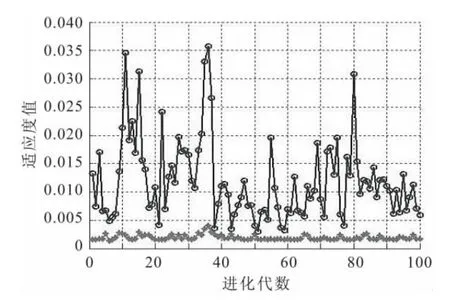
图7 基于PSO 的SVM 模型d1分量的参数选取Fig.7 Parameter selection of d1component in SVM model based on PSO
将上述所选取的各分量参数代入SVM 模型中对各分量值进行预测,可得到粒子群优化的WASVM 模型的预测结果。为了验证本模型的优越性,将粒子群优化的WA-SVM 模型的预测结果与WA-BP模型和单独SVM 模型进行了对比,见图8。WA-BP网络模型采用同样的小波分析和相空间重构,隐含层神经元个数为20,神经元传递函数使用S形函数;单独SVM 模型同样采用径向基核函数,通过反复试验选取核函数参数g=0.02、惩罚系数C=200。

图8 三种模型滑坡位移的预测结果对比Fig.8 Prediction results of landslide displacement time series by the three models
三种模型的预测精度见表3。由表3 可见,粒子群优化的WA-SVM 模型均方根误差RMSE 为0.96mm,小于WA-BP 模型和单独SVM 模型的;粒子群优化的WA-SVM 模型的平均相对误差绝对值为0.97%,也小于WA-BP 模型和单独SVM 模型的,表明粒子群优化的WA-SVM 模型具有较高的预测精度。
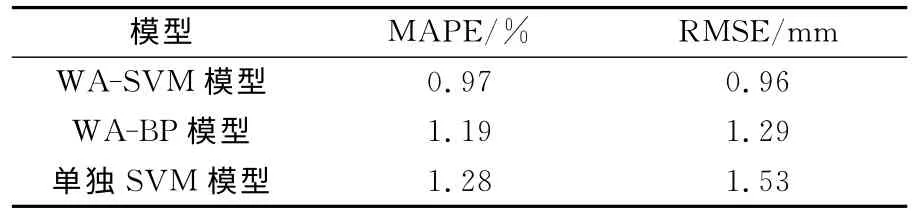
表3 三种模型的预测精度对比Table 3 Comparison of prediction precision of the three models
5 结论与建议
在分析滑坡位移序列混沌特性的基础上,将SVM模型及其改进的PSO 算法用于滑坡位移预测的实例分析中,并通过各模型精度对比得到以下结论:
(1)本文综合小波分析时频分解能降低噪声影响、支持向量机预测精度高的特点,提出了一种基于粒子群优化的WA-SVM 预测模型,实例预测结果表明,该模型能更准确地预报滑坡位移值,是一种可行、有效的滑坡位移预测方法。
(2)针对SVM 模型存在参数选取困难的缺点,使用参数寻优能力强的PSO 算法优化WA-SVM模型的参数选取过程,避免了人工选择参数效率低且未必能得到全局最优参数等问题,从而提高了WA-SVM 模型的效率和精度。
对于粒子群优化的WA-SVM 耦合模型,小波分解的层数、核函数的选取和粒子群优化算法是影响该耦合模型预测精度的关键因素。其中,小波分解层数目前主要采用的是经验尝试法,未形成系统的理论;SVM 模型核函数采用的是径向基核函数,但是对其他各种核函数的构建和性能分析还需要深入探讨。
[1]刘祖强,张正绿,邹启新,等.工程变形监测分析预报的理论与实践[M].北京:中国水利水电出版社,2008.
[2]李端有,陈卫兵.滑坡动力系统的混沌效应分析[J].长江科学院院报,2005,22(6):10-12.
[3]王东.GM(1,1)灰色模型在真空预压沉降预测中的应用[J].安全与环境工程,2012,19(4):145-148.
[4]张勇,关伟.基于最大Lyapunov指数的多变量混沌时间序列预测[J].物理学报,2009,58(2):756-763.
[5]胡启晨,胡斌,蒋海飞.BP人工神经网络在深基坑桩体位移预测中的应用[J].安全与环境工程,2013,20(3):154-158.
[6]范千,花向红.基于相空间重构与支持向量机预测滑坡位移的一种新方法[J].武汉大学学报·信息科学版,2009,34(2):248-251.
[7]Takens,F.Determining strange attractors in turbulence[J].Lecture Notes in Math,1981,89(8):361-381.
[8]Khemchandani,R.,Jayadeva,S.Chandra.Regularized least squares fuzzy support vector regression for financial time series forecasting[J].Expert Systems with Application,2009,36(1):132-138.
[9]宋星原,张国栋.基于WA-SVM 组合模型的流域月降雨量预测研究[J].长江科学院院报,2007,24(5):23-26.
[10]许冲,徐锡伟.基于不同核函数的2010年玉树地震滑坡空间预测模型研究[J].地球物理学报,2012,55(9):2994-3004.
[11]周创兵,陈益峰.基于相空间重构的边坡位移预测[J].岩土力学,2000,21(3):205-208.
[12]韩敏.混沌时间序列预测理论与方法[M].北京:中国水利水电出版社,2007:28-30.
[13]Kennedy,J.,R.C.Eberhart.Particle Swarm Optimization[A].In Proceedings of IEEE International Conference on Neural Networks[C].Perth,Australia,1995:1942-1948.
