激光差动共焦曲率半径测量不确定度评定

王 旭，王中宇，赵维谦，邱丽荣

（1.北京航空航天大学 仪器科学与光电工程学院，北京100191；2.北京理工大学 光电学院，北京100081）

引言

球面元件广泛地应用于紫外光刻机、天文望远镜、激光核聚变系统等精密光学系统，其中曲率半径是球面光学元件测量中最基本和最重要的参数之一［1-2］。目前常用的曲率半径测量方法有球径仪法、表面轮廓仪法、自准直仪法和干涉法等［3-5］。Trioptics公司Ultra-Spherotronic超精密球径仪的测量精度可达0.005%；松下电器公司UA3P超高精度3D表面轮廓仪的单点测量精度为10nm，可测最小曲率 半 径 为 2nm［6］；1992 年 Zygo 公 司 的 Lars A.Selberg提出了基于干涉法的曲率半径测量系统，测量精度可达0.001%［4］。球径仪法和表面轮廓仪法在测量的过程中均需要接触被测元件，容易造成零件表面的划伤，因此接触式测量法的应用受到一定限制［3］。干涉法具有测量精度高和灵敏度高的优点，但振动、温度和气流等容易对干涉条纹的判读产生干扰，对环境的要求十分严格［1，7］。

为了克服以上问题，我们提出了基于差动共焦法的曲率半径测量方法。此方法利用系统轴向响应特性曲线的过零点与标准透镜聚焦点相对应的特性，通过差动共焦轴向强度响应特性曲线IA和IB的过零点OA和OB，对被测球面元件的猫眼或共焦进行高精度触发瞄准，结合干涉测长技术测得猫眼和共焦位置之间的间距，进而实现曲率半径的高精度测量［8-10］。本文构建了一套激光差动共焦曲率半径测量系统，对曲率半径测量结果的不确定度评定进行研究，分析计算差动共焦曲率半径测量系统的精度和重复性。

1 激光差动共焦曲率半径测量系统设计

激光差动共焦曲率半径的测量原理如图1所示。当被测件位于“猫眼A”或“共焦B”位置的附近时，测量光束从被测件原路返回，经物镜和准直镜会聚后，被分束镜反射到分光棱镜BS。经BS分束后的2束测量光分别被“虚拟针孔1”和“虚拟针孔2”探测，2路虚拟针孔探测器分别具有-M和＋M的离焦量。

在测量时，分别对“猫眼”和“共焦”2个位置进行扫描，虚拟针孔探测到的光强相减就得到图1中的测量曲线，曲线的过零点分别对应于“猫眼”和“共焦”2个位置。在扫描的过程中，测长干涉仪分别记录“猫眼”的位置lA和“共焦”的位置lB，则被测件的曲率半径为

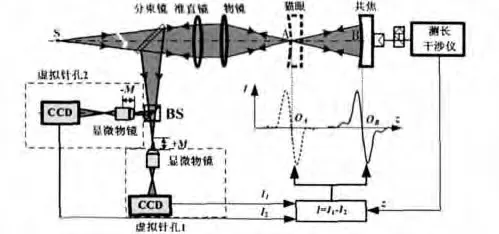
图1 激光差动共焦曲率半径的测量原理Fig.1 Laser differential confocal radius-ofcurvature measurement principle

所研制激光差动共焦曲率半径的测量系统如图2所示，主要由激光差动共焦主机、平移测长系统和主控系统等组成。

激光差动共焦主机选择波长为632.8nm、输出功率为5mW的半导体尾纤输出激光器，作为系统的点光源；准直镜选择消球差透镜，在633nm的波长下，fc＝500mm，D＝100mm；物镜选择口径为4寸（约133mm）、F／1.5的标准球面镜；虚拟针孔放置于行程为30mm的电动平移台上，便于对离焦量进行调整；虚拟针孔的CCD选用OKAM1100，其像素尺寸为s＝8μm、信噪比SNR＝100:1，显微物镜的放大倍数为40，虚拟针孔离焦量 M 为［9］

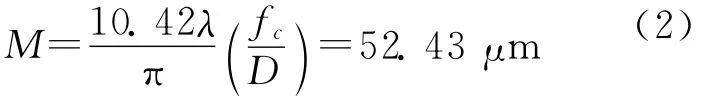
图2 激光差动共焦曲率半径测量系统Fig.2 Laser differential confocal radius of curvature measurement system

平移测长系统由测长干涉仪（DMI）、移动导轨和五维调整架组成。DMI选用Renishaw公司XL80型激光干涉仪，测长精度为±0.5ppm；移动导轨选用直线度误差为0.1μm的高精度大理石气浮导轨；气浮导轨的平移台上放置五维调整架，用于夹持被测件，五维调整架后面安装DMI测长所需的角锥镜。DMI的光轴与测量光路的光轴相重合，以消除由于测长光路与被测件轴线不重合带来的阿贝误差。气浮导轨选择移动范围为l＝600mm，平移台宽度为d＝200mm。

由于差动共焦主机选用的物镜焦距f物＝150 mm，能够测量的凸面最大曲率半径小于物镜焦距150mm，能够测量的凹面最大曲率半径为

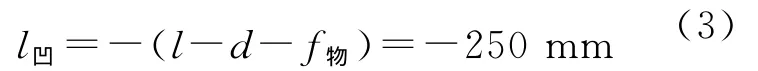
考虑到夹持被测件的安全性，曲率半径的测量范围为-200mm～100mm。

主控系统主要由计算机、监视器、图像采集卡、电机控制器、同步触发板卡等组成。其中图像采集卡采集2路CCD图像信号；同步触发板卡提供3路同步触发信号，分别触发2路CCD和测长干涉仪，保证图像信号和位移信号的同步。

2 激光差动共焦曲率半径测量实验

将Zygo公司的标准反射球面作为被测件，其标称曲率半径为R＝-12.7mm。测量时猫眼的位置坐标lA＝12.725 022mm；共焦位置坐标lB＝0.000 078mm，则被测件的曲率半径为

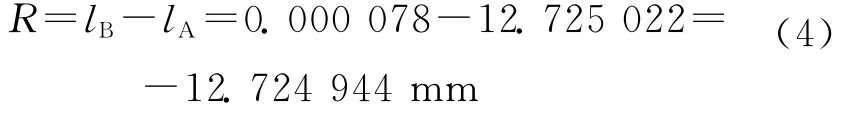
共进行2组测量，其中第1组测量15次，结果见表1。

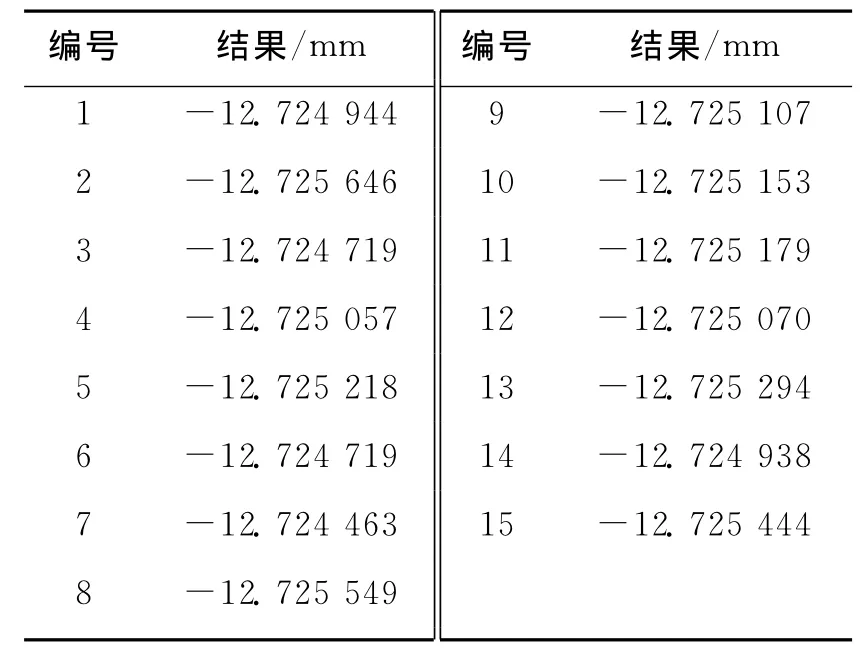
表1 第1组曲率半径测量结果Table 1 Group 1measurement result of radius-of-curvature

第2组测量3次，结果见表2。

表2 第2组曲率半径测量结果Table 2 Group 2 measurement result of radius-of-curvature

2组数据的相对误差为

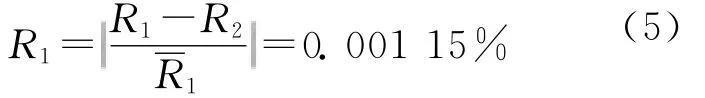
可见2组曲率半径的测量结果非常接近。

3 曲率半径测量结果的标准不确定度评定

3.1 贝塞尔评定法

根据贝塞尔公式，对2组激光差动共焦曲率半径测量数据分别进行标准不确定度评定，求得2组数据单次测量的标准不确定度分别为

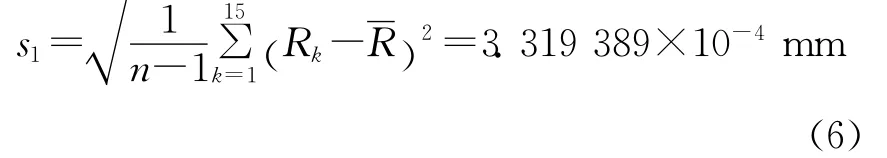
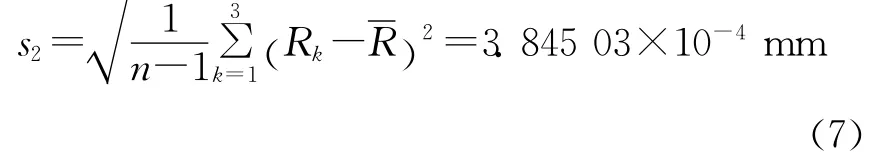
2 组数据之间标准不确定度的相对误差为

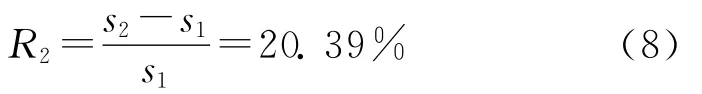
可见用贝塞尔公式评定标准不确定度时，数据量的大小对评定结果的影响比较大。因此，使用灰色评定法对第2组的测量不确定度进行评定。

3.2 灰色评定法

使用灰色理论给出的标准不确定度评定方法，对第2组数据进行标准不确定度评定。具体方法为：

将曲率半径测量结果数据的绝对值按从小到大进行排列，得：

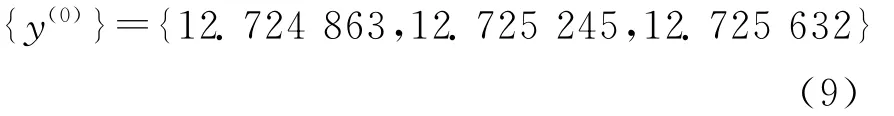
对｛y（0）｝做一次累加生成，得：

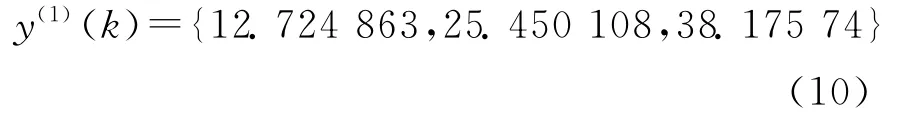
理想累加序列直线方程为

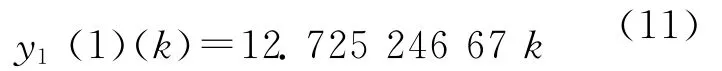
一次累加生成序列和理想累加曲线分别如图3所示，一次累加生成序列和理想累加曲线相差较小，表明测量数据的标准不确定度较小，最大差值在第2个数据，即：

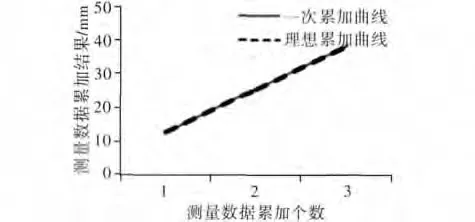
图3 测量结果的累加序列图Fig.3 Summation sequences of measurement results

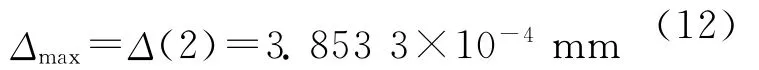
曲率半径测量结果的标准不确定度为

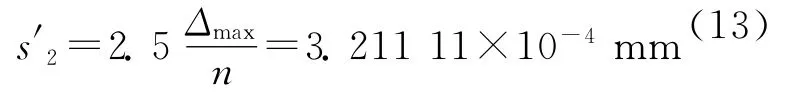
与第1组数据之间标准不确定度的相对误差为

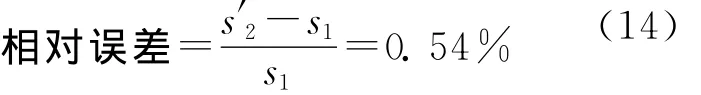
可见灰色评定方法对测量数据的样本量大小和分布规律的依赖性很小，在测量数据较少时也可获得较可靠的不确定度评定结果［11-13］。

对激光差动共焦曲率半径测量数据的标准不确定度评定结果表明，灰色评定方法在数据较少时比贝塞尔公式更具有可靠性；2组曲率半径测量结果的标准不确定度优于3.211 11×10-4mm，说明本测量系统具有较好的测量精度。

4 结论

通过构建激光差动共焦曲率半径测量系统实现曲率半径的高精度测量，被测件曲率半径的测量结果与标称值之间完全相符。对曲率半径测量结果进行标准不确定度评定的结果表明，激光差动共焦曲率半径测量系统具有较高的测量精度。

［1］ ANGELA D，TONY L，SCHMIT Z.Defining the measurand in radius of curvature measurements［J］.Recent Developments In Traceable Dimensional Measurements II，2003，5190：134-145.

［2］ TONY L S，NEIL G，MATTHEW V，et al.Improving optical bench radius measurements using stage error motion data［J］.Applied Optics，2008，47（36）：6692-6700.

［3］ DANIEL M.Optical shop testing［M］.USA：A John Wiley ＆Sons，Inc.，2007.

［4］ SELBERG L A.Radius measurement by Interferometry［J］. Optical Engineering，1992，31 （9）：1961-1966.

［5］ 王青，徐新华.干涉仪测量球面曲率半径的精度分析［J］.东南大学学报：自然科学版，2009，39（2）：55-59.WANG Qing，XU Xin-hua.Precision analysis of measurement of radius of curvature by interferometer［J］.Journal of Southeast University：Natural Science Edition，2009，39 （2）：55-59.（in Chinese with an English abstract）

［6］HIDEKI T，KEIICHI Y，HIROYUKI T.Ultrahigh accurate 3-D profilometer［J］.SPIE，2005，5190：387-394.

［7］ TONY L S，ANGELA D D，CHRIS J E.Uncertainties in interferometric measurements of radius of curvature［J］.SPIE，2001，5638：432-447.

［8］ ZHAO Wei-qian，SUN Ruo-duan，QIU Li-rong，et al.Laser differential confocal radius measurement［J］.Optics Express，2010，18（3）：2345-2360.

［9］ SUN Ruo-duan，QIU Li-rong，YANG Jia-miao，et al.Laser differential confocal radius measurement system ［J］. Applied Optics，2012，51 （26）：6275-6281.

［10］ 孙若端，邱丽荣，杨佳苗，等.激光差动共焦曲率半径测量系统的研制［J］.仪器仪表学报，2011，32（12）：2833-2838.SUN Ruo-duan，QIU Li-rong，YANG Jia-miao，et al.Development of laser differential confocal radius measurement system［J］.Chinese Journal of Scientific Instrument，2011，32（12）：2833-2838.（in Chinese with an English abstract）

［11］ WANG Zhong-yu，QIN Pin，GAO Yong-sheng.Grey evaluation of measurement uncertainty［J］.Journal of Grey System，1999，11（4）：347-352.

［12］ ZHU Jian-min，WANG Zhong-yu，BIN Hong-zan.A grey evalution model of measurement uncertainty［J］.The Journal of Grey System，2000，12（3）：207-214.

［13］ 朱坚民，宾鸿赞，王中宇，等.测量结果标准不确定度的灰色评定方法［J］.华中理工大学学报，2000，28（9）：84-86.ZHU Jian-min，BIN Hong-zan，WANG Zhong-yu，et al.A grey evaluation method of measurement result with standard uncertainty［J］.Journal of Huazhong U-niversity of Science and Technology，2000，28（9）：84-86.（in Chinese with an English abstract）