有限元法分析带钢在拉弯矫直过程中的能耗值①

马国财 周存龙 赵培建，3 李伟娜 李中喜

(1:太原科技大学山西省冶金设备设计理论与技术重点实验室 山西太原030024;

2:山东日照钢铁集团有限公司 山东日照276806;

3:山东钢铁集团济南钢铁公司 山东济南250001;

4:中冶东方工程技术研究院有限公司 山东青岛266555)

1 前言

拉伸弯曲矫直机在带钢生产线中主要用于改善板型质量以及除鳞，针对拉弯矫研究的文献大部分是关于拉弯矫基本原理的简单描述和定性分析，拉弯矫机理并未完全揭示，尤其是实际生产中拉弯矫直过程的描述问题还存在着难以量化的问题。由于拉弯矫过程较为复杂，准确定量地描述这一过程非常关键。实际生产中，由于拉弯矫直设备的传感器种类和数量有限，只能采集特定位置的几种参数，要想对拉弯矫过程进行全面分析较为困难。因此，结合设备参数和现场工艺参数建立全尺寸的有限元模型，对研究实际生产中的拉弯矫直变形机理，定量地描述各工艺参数具有重要意义。

国内外相关学者对拉弯矫直过程的有限元建模做了大量工作，Hoon Huh等人利用Abaqus/Standard有限元分析软件对强化弹塑性带材的拉伸弯曲过程进行了仿真［1］，J.W.Morris等人利用Abaqus/Standard有限元分析软件建立了一个基于实验室拉矫机的初级有限元模型［2］，F.Yoshida等人开发了有限元分析软件，并利用其对金属带材拉伸弯曲矫直进行分析［3］，Norman Mathieu等人用Abaqus/Explicit分析了张力辊后的平直度缺陷问题［4］，L Steinwender等人用Abaqus/Explicit建立了带钢曲率分布和功率损失模型［5］，李天浩等人运用MARC有限元软件对宽带钢拉伸弯曲矫直变形过程进行大量工况的数值仿真计算［6］。

然而，为了节省计算成本，其中大部分有限元模型经过简化，一般取模型的一半或四分之一进行建模，也未与实际生产中的生产参数做比较，这样就不能较为真实地反应实际生产中的拉弯矫直过程。因此，依据国内某钢厂冷轧酸洗线拉矫设备相关生产参数，建立了全尺寸的拉弯矫直过程有限元模型，并与实际生产过程进行对比，最终建立了与实际生产参数吻合度较高的有限元模型，为后续进一步研究拉弯矫直过程打下基础。

2 带钢拉伸弯曲矫直的有限元建模

2.1 拉伸弯曲矫直过程中的结构及工艺参数

某钢厂拉弯矫设备采用了两弯一矫的矫直方式，辊系结构如图1。

图1 拉弯矫直机辊系布置示意图

张力辊:(1、2、3、4);导向辊:(5、8、9、12、13、15);弯曲辊:(6、7、10、11、14);带钢:(16)

如图1示，张力部分由1#～4#张力辊组成，且四个张力辊的速度依次递增，以此产生矫直所需张力。矫直部分由1#、2#两个弯曲单元及一个矫直单元组成:1#弯曲单元包括5、6、7、8 辊，2#弯曲单元包括9、10、11、12 辊，矫直单元包括13、14、15 辊。

表1 拉矫设备参数、张力辊速度及带材参数表

如表1所示:张力辊辊径1250mm，辊面覆盖聚氨酯层;弯曲辊辊径80mm，使通过的带材产生反复弯曲;导向辊辊径250mm;辊子长度均为1900mm。经过减速箱减速之后，四个张力辊的转速分别为:71.3m/min，71.6m/min，72.3m/min，72.6m/min。带钢型号为Q315，宽度1275mm，厚度3.5mm，密度7850kg/m3，弹性模量2.06×1011Pa，泊松比0.3。

表2 拉弯矫各辊系压下量表

某批次带钢的矫直过程中，根据厂内制定的标定方法，采用的压下量组合如表2所示:其中1#、2#弯曲单元压下量均为50mm，矫直单元压下量为25mm。

2.2 拉伸弯曲矫直过程的有限元建模

采用ANSYS/LS-DYNA进行有限元建模，结构参数、工艺参数及带钢的材料属性按实际生产参数设定。

板带单元为Solid164，材料采用双线性各向同性硬化，板带厚度方向单元数为6，宽度方向单元数为10，长度方向单元长度为5mm，单元总数为317120，节点数为399069;所有张力辊、弯曲辊及矫直辊单元均选用壳体Shell163，材料均采用刚体。模拟时长0.1s，单个模型计算时间108h。拉弯矫网格划分模型及有限元模型如图2所示。

图2 拉弯矫网格划分模型及有限元模型

3 有限元计算结果与实际生产数据的对比

采用LS-Prepost分析计算结果，并将模拟所得功率值与实际生产数据进行对比。

3.1 实际功率计算

实际生产过程中的总功率为:

其中:P1、P2、P3、P4分别为 1#、2#、3#、4#电机的实际功率，P1=P额1× ηp1=35kW ×53.7%=18.795kW，P2=P额2×ηp2=70kW×53%=37.100kW，P3=P额3× ηp3=350kW ×25.6%=89.600kW，P4=P额4×ηp4=190kW ×25.9%=49.210kW

而:P额1、P额2、P额3、P额4为四个电机的额定功率，如表3示。

表3 电机额定功率表

图3 现场电机负载比

且:ηp1、ηp2、ηp3、ηp4分别为1、2、3、4电机功率负载比，如图3示。

η1、η2、η3、η4分别为1#、2#、3#、4#减速箱的传动效率，由图4和表4可知。

3.2 模拟功率计算

待运行稳定之后，绘制一段时间内的总能量曲线，并线性拟合。如图5所示。

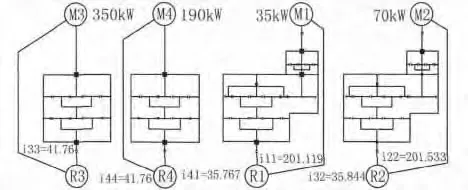
图4 拉弯矫传动系统

表4 各传动机构传动效率表

图5 能量拟合曲线

图5中，能量拟合直线的斜率即为总功率值，可知:

直线斜率为:

k=147642.3021

即模拟总功率为:

P模=147.6423021kW

3.3 实际功率与模拟功率对比

由上述分析知，实际总功率为:

P实=157.39kW

模拟总功率为:

P模=147.6423021kW

因此，模拟功率与实际功率的差值为:

PΔ=157.39-147.64=9.75kW

由此得出模拟功率和实际功率的误差值为:

4 结论

经加载计算后，将模拟所得功率值与实际生产过程中的电机功率进行对比。考虑到有限元模型只对拉弯矫设备辊系进行建模，且材料模型和单元类型与实际材料属性有一定差异，还考虑到沙漏能损耗等问题，最终得出两者误差为6.19%。这说明所建有限元模型与实际工况吻合度较高，此有限元模型可以作为实际生产的参考，为之后全面分析实际生产中的拉弯矫过程提供了较为可靠的有限元模型。

［1］Hoon Huh，Hyoung Wook Lee，Sang Rae Park，et al.The Parametric Process Design of Tension Levelling With an Elasto-Plastic Finite Element Method［J］.Journal of Materials Processing Technology，2001，113(1-3).

［2］Morris J W，Hardy S.It Lees A W，et al.Formation of Residual Stresses Owing to Tension Levelling of Cold Rolled Strip ［J］.Ironmaking and Steel making，2001，Vol.28(1):44-52.

［3］Yoshida F，Urabe M.Computer-Aided Process Design for Tension Levelling of Clad Sheet Metal［J］.Key Engineering Materials，2000，177-180，503-508.

［4］Norman Mathieu，Régis Dimitriou，Anthony Parrico，Michel Potier-Ferry，Hamid Zahrouni.Flatness defects after bridle rolls:a numerical analysis of leveling［J］.Mater Form(2013)6:255-266.

［5］L Steinwender，A Kainz，K Krimpelstätter，K Zeman.Computational Analysis of the Curvature Distribution and Power Losses of Metal Strip in Tension Levellers［J］.Materials Science and Engineering 10(2010)012135.

［6］LIU Tianhao，ZHANG Qingdong，ZHU Jianru.Simulation of the Wide Strip Deformatio During Tension Leveling by FEM［A］.The Chinese Society for Metals，eds.Proc of Annual Meeting，CSM 2005 ［C］.Beijing，China:Metallurgical Industry Press，2005.550-552(in Chinese).