烧结环冷机液密封数值仿真研究①
2014-11-06张家元张加楠田万一
张家元 张加楠 田万一
(中南大学能源科学与工程学院 湖南长沙410083)
鼓风式环冷机是烧结矿冷却工序中普遍应用的设备,国内外许多学者对其冷却过程及余热回收利用进行了大量研究[1-5],但对其密封部件关注较少。而环冷机密封性能的好坏直接关系到烧结矿冷却效率及余热利用率[6-7]。传统密封性能差,漏风严重,导致环冷机冷却能力下降,风机能耗高,环冷机故障率增加[8-10]。最新型的液密封环冷机采用液体作为其动密封环节的介质,能实现漏风率降低5%以内的密封效果,相比传统鼓风环冷机接近30%漏风率,是一个巨大的提升[11]。
但是,新型液密封环冷机在运行过程中,特别是风机启停时会出现液面强烈波动甚至激起水花,水花被高速气流带入台车,严重影响烧结矿的质量。另外,若液面的上下波动过于剧烈,出现液面低于侧面挡板底部时,风会从底部向外泄漏,同时引起水溢出,使密封失效,环冷机无法正常工作。
由于液密封环冷机应用时间较短,国内外相关研究少,为保证液密封稳定运行,亟需了解各参数变化对液密封的影响。基于VOF方法在气液两相流研究中被广泛应用[12-15],本文将以 VOF为主要研究方法,对环冷机启动时液密封的进口风速、出口压力、水槽液位、初始状态设定几种工况,借助计算机仿真技术,对不同工况进行模拟,并以保证液密封更平稳运行为目的,提出液密封最佳运行参数组合。
1 模型的建立
1.1 物理模型
1)图1是环冷机液密封部分的三维模型,下部方形管道是与风机连接的进风口,上部圆管为液密封出风口,与台车相连。由于台车以半径20m做环形运动,出风口亦会跟着移动,速度为0.03m/s左右。图2为液密封的断面图,环形风道的内、外液封是由环形液槽和悬吊的门型密封板组成。内环槽与环形风道连通,外环槽与大气连通。液槽高度0.9m,门型密封板距离液槽底0.1m,内外环槽槽宽0.15m。

图1 环冷机液密封结构
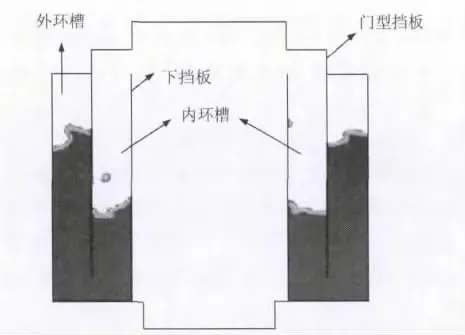
图2 液密封截面图
2)在对风道内空气流动进行三维模拟中,由于液密封环冷机上部台车环形运动速度非常缓慢,所以不考虑出口移动的影响,并对物理模型做以下简化:
(1)环冷机启动工况稳定,在计算时间内,各操作参数均为恒定值,没有波动变化;
(2)研究对象为空气流经区域,故固体壁面看作无滑移边界,靠近壁面处的边界层采用标准壁面函数处理;
(3)进口空气马赫数Ma<0.3,可视为不可压缩流体。流场内空气密度不随压强、温度差异变化。
1.2 数学模型
控制方程采用以速度和压力为变量的不可压缩粘性流体的Navier-Stokes方程和连续性方程:
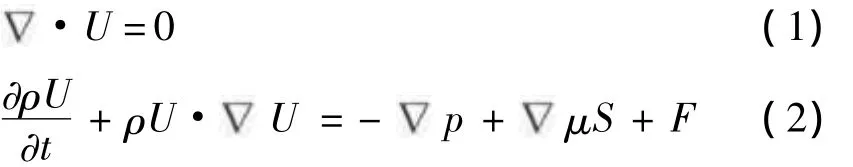
式中 ρ—密度;
U—流速矢量;
t—时间;
p—压力;
μ—动力粘性系数;
F—体积力,包括重力和表面张力的作用。湍流模型采用标准k-ε模型,其中湍动能为k,耗散能为ε,其k方程与ε方程分别为:
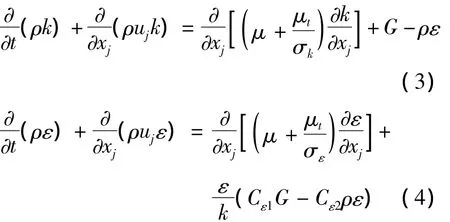
其中:
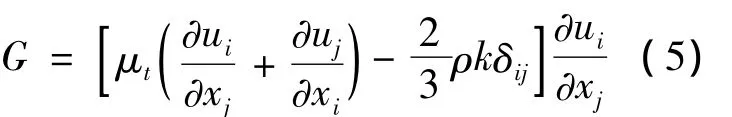
式中湍流黏性系数μt= ρCμk2/ε,Cμ、Cε1、Cε2、σk、σε均为 k- ε 方程中的常数,分别取值为0.09、1.44、1.92、1.0、1.3,δij为克罗内克数。
采用VOF方法实现对气液两相流界面的追踪,体积分数函数αq定义为单元内第q相流体所占有体积与该单元的体积之比。即若αq=1,则表示单元内全部为第q相流体;若αq=0,则说明单元内没有第q相流体;若0<αq<1,则该单元为交界面单元。对于本文,由于只有气液两相,故q=1或2。
1.3 边界条件
根据环冷机液密封的工作原理来看,模型边界有以下几个部分:气体入口、与大气连通的外环槽口、壁面、气体出口。对于气体入口,采用速度流量入口边界条件;对于与大气连通的外环槽口,采用压力入口边界条件;认为壁面处的流体速度为0,即无滑移壁面边界条件;对于出口,采用压力出口边界条件。
2 计算结果与分析
2.1 单因素影响分析
利用已建立的计算模型,针对影响水槽液面波动的4个主要参数:进口风速、出口压力、水槽液位、初始状态,在其他参数值不变的情况下,研究单一参数对液面波动过程的影响规律。其中水槽液位指风机未开启时水槽的液面高度,初始状态指的是环冷机启动时门型挡板振动导致的初始液面波动高度。本计算以环冷机液密封实际初始运行工况为基准工况,相应的操作参数分别为:进口风速20m/s,出口压力3600Pa,水槽液位0.5m,初始状态0.03m。
1)进口风速
不同进口风速条件下内槽液面最高和最低值随时间变化曲线如图3和图4所示。

图3 风速对液面最高值的影响
由图3和图4可知,进口风速越大,内槽液面最高值越大,但均随时间增加而迅速减小;而不同速度条件下液面最低值的曲线基本重合,即液面最低值的变化基本相同,说明液面最低值变化受进口风速的影响较小。内槽液面最低值的曲线均呈现先下降后上升再下降的趋势,并最终将趋于一水平直线。而不同速度条件下液面最高值的曲线则明显不同,风速越大,液面波动越剧烈,说明进口风速更多影响气液两相界面,对液位的影响较小。
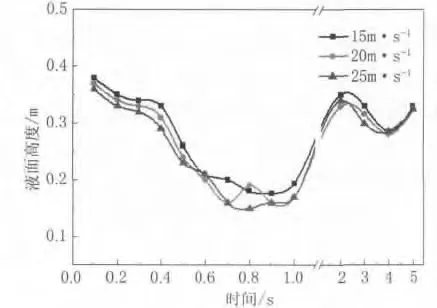
图4 风速对液面最低值的影响
2)出口压力
不同出口压力条件下内槽液面最高和最低值随时间变化曲线如图5和图6所示。
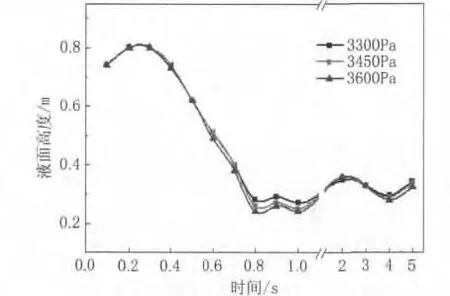
图5 出口压力对液面最高值的影响

图6 出口压力对液面最低值的影响
由图5和图6可知,在0.7s前,不同出口压力条件下曲线基本重合,即内槽初始液面在不同压力下基本相同。但在0.7s之后,液位高度差表现出轻微不同,即此时出口压力不同对于液面高度不产生影响。这是因为液槽上方的空气流速受密封液体阻挡而减小,动压转化为静压。不同出口压力的空气在内槽上方的静压不同,则内槽液位表现出不同的高度。因此出口压力更多影响液位,而对气液两相界面几乎没有影响。
3)水槽液位
不同液位条件下内槽液面最高和最低值随时间变化曲线如图7和图8所示。
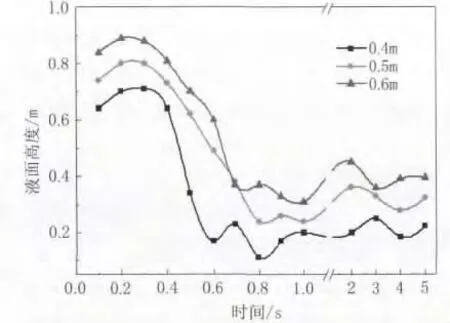
图7 液位对液面最高值的影响
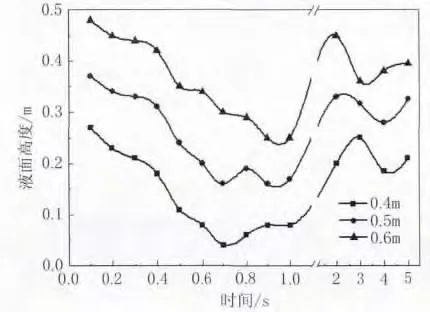
图8 液位对液面最低值的影响
由图7和图8可知,初始液位高度不同,液面最高值与最低值也相应不同,表现在图中即各曲线均不重合。初始液位为0.4m、0.5m、0.6m 的液面曲线具有相同变化规律,3条的曲线之间基本保持0.1m的高度差,这与初始液位之间0.1m的高度差是完全符合的,因此液位高度对液面波动基本没有影响。但液位为0.4m工况下,内环槽在0.6s时刻出现液面最低值低于0.1m的状态,导致风从水槽底部泄漏。说明水槽液位虽不影响气液两相界面状态,但对液密封稳定运行影响极大。
4)初始状态
不同初始状态条件下内槽液面高度最高和最低值随时间变化曲线如图9和图10所示。

图9 初始状态对液面最高值的影响

图10 初始状态对液面最低值的影响
由图9和图10可知,由于初始液面状态的不稳定,液面最高值曲线呈现明显不同的分布规律。初始波高为0.04m工况下,内环槽液面最高值曲线稳定在1m,从0.2s一直持续到0.6s,这是由于内槽液面剧烈震荡激起了水花冲击在顶部密封板。但0.6s之后曲线呈现直线下落,这是空中的液滴回落的过程。在1s后液面最高与最低曲线基本重合,即液面震荡过程结束,恢复平稳。而初始波高在0.03m与0.02m的曲线与0.04m的曲线也具有相似的规律,但曲线震荡的幅度越来较小。液面最低曲线在不同初始波高下则基本一致。综上,初始波高对内槽液位的变化影响较小,但对气液两相界面的影响十分巨大,很容易引起液密封的不稳定。
2.2 正交仿真实验
利用正交实验法对进口风速、出口压力、水槽液位、初始状态这4个参数进行综合分析。以上4个参数均为3水平,故选择正交表L9(34)。实验优化指标为同一水槽内液面最高点与液面平均高度之差,即 ΔH=Hmax—Havg。ΔH 值越小,表征液面越平稳。若某一时刻出现液面跳出水花,则以水花所在高度作为Hmax的值。正交实验设计如表1所示。

表1 正交实验工况仿真计算结果
根据方差分析可以发现不同因子对实验结果的影响显著性依次为:初始状态、进口风速、水槽液位、出口压力。通过Fluent进一步模拟仿真结果表明,在考虑因素单独作用的条件下,各参数最优水平组合为:进口风速 15m/s,出口压力3300Pa,水槽液位 0.5m,初始状态 0.02m。得到最优工况下ΔH平均值为0.048m。
3 计算结果验证
考虑到液密封的密闭性,对于内环槽的现场测试有一定的难度,因此通过易于观察测量的外环槽液面高度变化的现场测试值与仿真结果的数值进行对比,对本研究所采用模型的正确性进行验证。针对液密封外环槽液面高度计算结果与测试结果的对比如下表2所示。
从表2可以看出,在数值仿真结果和测试结果之间存在不同程度的误差。该误差主要来源于:①测试过程中环冷机液密封各项参数并非保持恒定不变,例如鼓风机出口风压和流量存在波动,这将对测试结果产生直接的影响;②现场测试工具及测试人员操作可能存在一定误差;③本计算对物理模型进行了一定程度的简化可能产生误差。但是,数值仿真结果与现场测试结果的最大误差小于5%,且液面波动与实际趋势也较为符合,因此,可以认为本文所建立的模型及计算结果是可靠的。
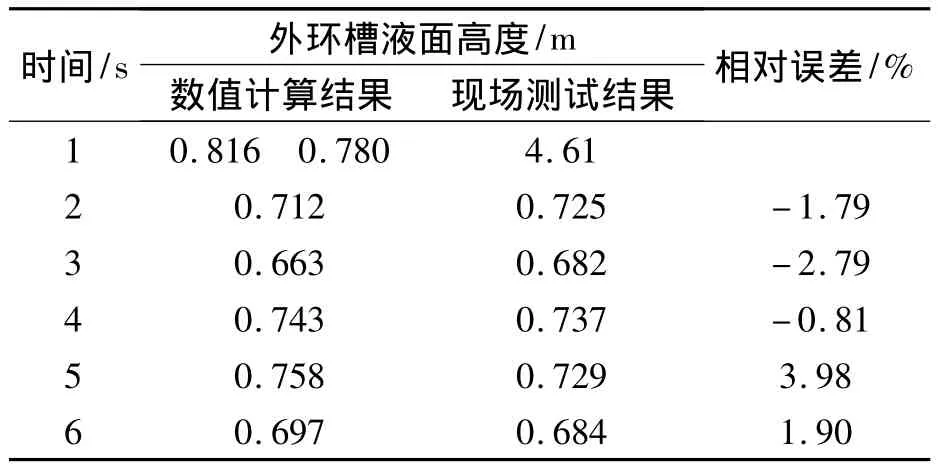
表2 液密封外环槽液面高度计算结果与测试数据的对比
4 结论
1)利用VOF方法很好地模拟出液密封水槽液面波动,较好地捕捉出气液两相流的分界面,计算结果与现场测试之间的误差在5%以内,验证了此模型的正确性。
2)通过上述模型计算了在其他参数正常的情况下,各单一参数对液密封液面的影响。其中液面初始状态及进口速度对液面平稳性有较大影响,液槽液位及出口压力则主要影响液位的变化。
3)运用正交实验综合分析了影响液密封水槽波动的主要因素,初始状态影响最大,进口风速和水槽液位影响次之,出口压强最小,并进一步计算得到液密封最优运行参数组合:进口风速15m/s,出口压力 3300Pa,水槽液位 0.5m,初始状态0.02m。
[1]赵斌,张玉柱,王子兵,等.烧结环冷机热工测试及余热源参数确定[J].钢铁,2010,Vol.45(8):90-93.
[2]Leong J C,Jin K W,Shaiu J S,et al.Effect of sinter layer porosity distribution on flow and temperature fields in a sinter cooler[J].International Journal of Minerals,Metallurgy and Materials,2009,Vol.16(3):265-272.
[3]JANG Jiinyuuh,CHIU Yuwei.3-D transient conjugated heat transfer and fluid flow analysis for the cooling process of sintered bed[J].Applied Thermal Engineering,2009,Vol.29(14):2895-2903.
[4]张家元,田万一,戴传德,等.环冷机分层布料仿真与优化[J].化工学报,2012,Vol.63(5):1385-1390.
[5]Feng Junxiao,Liang Kaili,Sun Zhibin,et al.Cooling process of iron ore pellets in an annular cooler[J].International Journal of Minerals,Metallurgy and Materials,2011,Vol.18(3):285-291.
[6]唐先觉.我国烧结行业的技术进步[J].烧结球团,2008,Vol.33(2):1-4.
[7]董辉,赵勇,蔡九菊,等.烧结-冷却系统的漏风问题[J].钢铁,2012,Vol.47(1):95-99.
[8]甘牧原,唐建波,马承胜,等.柳钢球团环冷机密封的改造[J].烧结球团,2008,Vol.33(3):29-31.
[9]陈东风,王军,路要通.球团环冷机水密封的改造[J].河南冶金,2009,Vol.17(6):35-37.
[10]罗可,汤清铭.液密封环冷机台车密封单元串风问题的改进与探讨.烧结球团,2010,Vol.35(4):10-12.
[11]郭清,高德亮.液密封环冷机风道水密封镇波装置的研究与应用[J].烧结球团,2012,Vol.37(3):19-20,30.
[12]董志,詹杰民.基于VOF方法的数值波浪水槽以及造波、消波方法研究[J].水动力学研究与进展,2009,Vol.24(1):15-21.
[13]李玲,陈永灿,李永红.三维VOF模型及其在溢洪道水流计算中的应用[J].水力发电学报,2007,Vol.26(2):83-87.
[14]李春利,李建慈,刘继东,等.用VOF法模拟导向立体传质塔板罩内两相流[J].化工学报,2007,Vol.58(4):881-886.
[15]袁丽蓉,沈永明,郑永红.用VOF方法模拟静止浅水环境中的垂向紊动射流[J].水科学进展,2004,Vol.15(5):566-570.
