多杂质氢网络矩阵法的混合互补规律研究

李 立，刘桂莲

（西安交通大学 化学工程与技术学院，陕西 西安 710049）

氢气是石油催化裂化和加氢重整等装置生产低杂质轻质油品的重要原料。如今，市场对轻质馏分油的需求持续增加，致使氢气的需求持续增长，氢气供应成为炼油厂的难题。通过氢网络集成技术减少炼油工业对氢气的需求是高效的节氢途径，有重要的意义。

氢网络的设计和优化主要有氢夹点法［1-7］和数学规划法［8-15］。夹点法简明易懂，物理意义明确，但只能用于单杂质的氢网络；数学规划法可考虑多杂质和多种约束，但不能保证获得全局最优解。Liu等［16］提出的矩阵演化法可用来解决多杂质氢网络的匹配和设计问题。该方法既可得到多杂质氢网络系统的最小新氢用量，也可设计出对应的氢气分配网络［17-19］。但该方法假定混合互补的两个氢源在混合后与该氢阱匹配时的关键杂质不变，忽略了混合互补的氢源在混合后与氢阱匹配的关键杂质可能会发生变化的情况。因此，该方法的混合互补判断规则不准确。

本工作对混合互补的规则进行了系统研究，分析推导出用于判定混合互补的参数，通过参数的比较来判定最优的匹配源，改进混合互补的识别方法。此外，还对原矩阵法在计算混合互补时存在的漏洞提出相应的改进方案，使得矩阵演化法在解决氢网络的设计问题时更加简便和准确。最后用改进后的矩阵演化法对某氢网络进行了设计和优化。

1 矩阵演化法的设计步骤

对于一个有m股氢源、n股氢阱和nc种杂质的多杂质系统，每股氢源（SRi，i=1，2，…，m）有一定的流量（FSRi）和杂质k（k=1，2，…，nc）浓度（CSRik）；每股氢阱（SKj，j=1，2，…，n）的流量和进口杂质浓度分别为FSKj和CSKjk。氢阱进口需满足如下约束条件：

1.1 最大匹配流量矩阵

对于每一对氢源氢阱，根据每个杂质k都能计算出一个相应的最大可能匹配流量（MPijk），如式（2）所示。

对于每一个氢阱，可根据式（2）计算出它与各氢源匹配时的MPijk，并写入同一个最大可能匹配流量矩阵：

在该矩阵中，每一行对应一个氢源，每一列对应一个杂质，每一个元素对应相应的氢源和氢阱匹配时根据对应杂质计算出的MPijk。取每一行的最小元素为Mij，即

所得的每个Mij写入一个矩阵，可得最大匹配流量矩阵（M矩阵）：

在该矩阵中，每一行对应一个氢源，每一列对应一个氢阱，每一个元素对应相应的氢源和氢阱的最大匹配流量。在该匹配流量时，一种杂质的浓度达到氢阱的上限要求，则该杂质即为该对氢源氢阱匹配时的关键杂质，而其他杂质的浓度均小于其上限要求。

1.2 确定潜在匹配流量矩阵

M矩阵给出了每一股氢阱与各股氢源匹配时的最大匹配流量。氢阱在最大匹配流量下与任意氢源匹配时，相应的关键杂质浓度将达到上限，因此该氢阱不能同时与多股氢源在最大匹配流量下匹配。根据M矩阵氢阱SKj列中非零元素对应的关键杂质相同与否，可识别该氢阱的潜在匹配氢源和相应的潜在匹配流量（Pij），这一确定过程分为如下两种情形：

1） 非零元素对应相同的关键杂质，选取具有最大Mij的氢源作为该氢阱的潜在匹配氢源，相应的最大匹配流量为Pij。而该氢阱与其他氢源之间的Pij设为0，即

2） 非零元素对应不同的关键杂质，需考虑混合互补优势。若氢源SRp和SRq与氢阱SKj匹配的关键杂质分别为KIpj和KIqj，则两氢源的关键杂质浓度满足：CSRpKIqj＜CSRqKIqj且CSRqKIpj＜CSRpKIpj，则这两个氢源与该氢阱匹配时存在混合互补。此时两氢源混合与该氢阱的匹配流量大于其中任一氢源与该氢阱的匹配流量。最大匹配流量时，两种杂质的浓度同时达到氢阱进口上限，其他杂质的浓度不能超过该上限，可根据式（6）求得各氢源的混合流量。

对于一个氢阱，需算出所有具有混合互补优势的氢源的最大匹配流量，选择匹配流量最大的一个或一组氢源作为该氢阱的潜在匹配源，其他氢源与该氢阱的Pij为0。若氢源之间无混合互补优势，则根据上述情形1）来确定潜在匹配源和Pij。

将结果写入矩阵得到潜在匹配流量矩阵（P矩阵）：

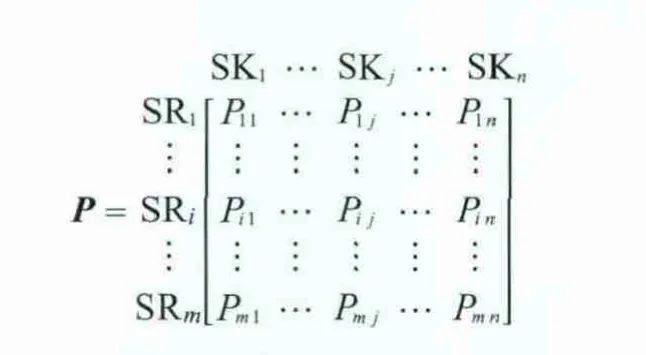
1.3 最佳匹配流量矩阵

在M矩阵和P矩阵的确定中，仅考虑了杂质浓度的约束。要得到最佳匹配流量，还需考虑氢源和氢阱的流量约束，其确定过程同样分为两种情形：

将每一股氢阱的Oij列入矩阵中，便得到最佳匹配流量矩阵（O矩阵）：

2 混合互补规则的改进

氢源与氢阱的杂质浓度之比可反映杂质浓度的相对大小，用于判断关键杂质。如某氢源氢阱系统有nc种杂质，则各氢源与氢阱的杂质浓度比矩阵（R矩阵）如下：

氢源与氢阱匹配时的关键杂质对应各杂质浓度比的最大值，如式（7）所示。因此不需像现有的矩阵法一样，求取每一对氢源氢阱匹配时的Mijk。

若氢阱中某些杂质的进口浓度上限为0，则氢源与氢阱的杂质浓度比矩阵会发生相应改变，需根据氢源的对应杂质浓度做相应的调整，具体规则如下：若氢源的对应杂质浓度为0，在式（7）中不考虑这种杂质；若氢源的对应杂质浓度不为0，说明此氢源不能与该氢阱匹配，可去掉相应氢源的对应行。

现行矩阵法中，分析氢源SRp和SRq与氢阱SKj匹配是否混合互补时，仅考虑了这两种氢源分别与该氢阱匹配时的关键杂质KIpj和KIqj，而未考虑其他杂质的浓度在混合后的变化。这种方法实际上是假定混合互补的两个氢源在混合后与该氢阱匹配时的关键杂质不变，仍为这两个氢源在混合前匹配时的关键杂质。但混合互补的氢源在混合后与氢阱匹配的关键杂质可能会发生变化。若直接根据式（6）计算混合互补所得氢源的混合量下，其他杂质的浓度可能会超过相应氢阱的上限要求。这种情况下，基于关键杂质不变所得的匹配不可行，在此基础上所得的整个氢网络的优化结果也不可行。因此，在分析氢源之间的混合互补时，仍需考虑其他杂质的浓度变化。本工作将对混合互补的规则进行系统的研究，并对混合互补的识别方法进行改进。

本节将对表1所示的氢源氢阱系统进行分析。该系统中有3种杂质，分别为A，B，C。对于该系统，若

则说明SRp与SKj匹配的关键杂质是A，SRq与SKj匹配的关键杂质为B，SRp和SRq可以混合互补。SRp和SRq的混合互补量可根据式（12）～（14）计算。

表1 含3种杂质的氢源、氢阱数据Table 1 Data of hydrogen sources(SR) and hydrogen sink(SK)with three impurities

式（12）～（14）分别变换可得：

由式（15）和式（16）可知式（17）必成立，则式（14）也成立；若式（18）或式（19）不成立，则式（17）不一定成立，同样，与式（17）对应的式（14）也不一定成立，这取决于式（12）和式（13）联解的结果。

联立式（12）和式（13）可得：

将式（20）和式（21）代入式（17），化简得：

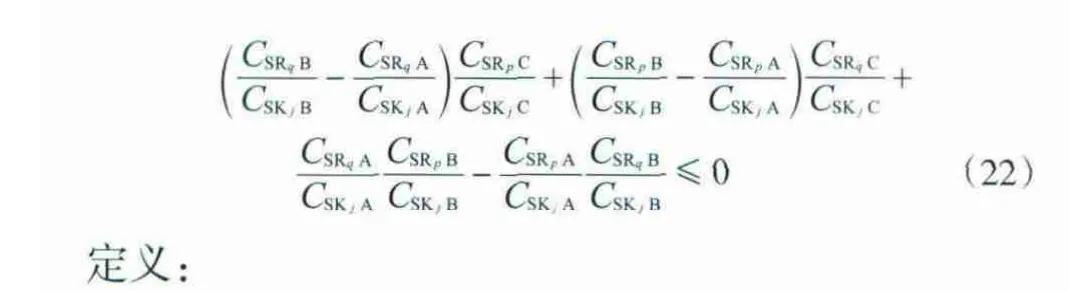
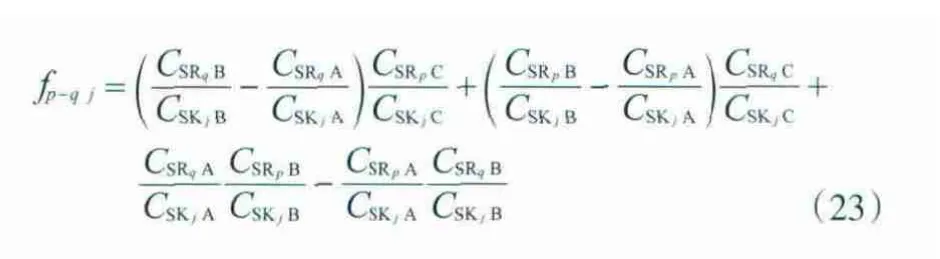
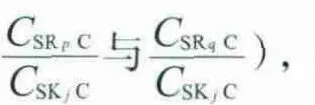
例如：对于表2所示的简单氢网络，根据现有的矩阵法，SR1和SR2与SK匹配的关键杂质分别是N和H2S；两种氢源SR1和SR2混合互补，混合流量分别为：M′SR1=16.37 m3/h，M′SR2=3.64 m3/h。

但当两种氢源在该流量下混合与氢阱匹配时，杂质CO和I的浓度均超过氢阱的允许上限。因此，虽然两个关键杂质的浓度满足氢阱的要求，但两个非关键杂质的浓度不能满足氢阱的要求。这说明用现行的混合互补方法识别出的混合互补氢源或混合互补量不正确。

表2 简单氢网络的氢源、氢阱数据Table 2 Data of hydrogen sources and hydrogen sink for simple hydrogen network

考虑关键杂质发生变化的情况，根据杂质CO和I分别计算得：f1-2CO=0.620，f1-2I=0.147，说明混合互补后关键杂质发生了变化。因为f1-2CO＞f1-2I，所以变化后的关键杂质应是CO以及N和H2S二者之一。假定混合互补后的关键杂质是CO和N，根据方程组（6）求解可得：M′SR1j=16.64 m3/h，M′SR2j=2.67 m3/h。在这种混合流量下验算其他杂质，H2S与I的浓度均未超过氢阱的杂质上限。因此，氢源SR1与SR2可以混合互补，且混合互补后的匹配流量为19.31 m3/h，关键杂质为CO和N。

通过上述结果的比较可知，新方法可使现行方法认为的一些不可能进行混合互补的氢源可能发生混合互补，弥补了现行方法的不足。

3 混合互补氢源选择方法的简化

现行矩阵法在选取混合互补氢源时需求解数目巨大的方程组，如只含有两种杂质的6股氢源、4股氢阱的氢网络，最多需求解36个方程组。因此，探求只需进行简单计算就能判断出最佳混合互补氢源的方法很有必要。

对于表3所示的氢网络，若氢源SRp和SRq混合互补与SKj匹配，且SRp与SKj匹配的关键杂质为A，SRq与SKj匹配的关键杂质为B，由式（20）和式（21）可得SRp和SRq混合互补与SKj匹配的总流量表达式，见式（24）。

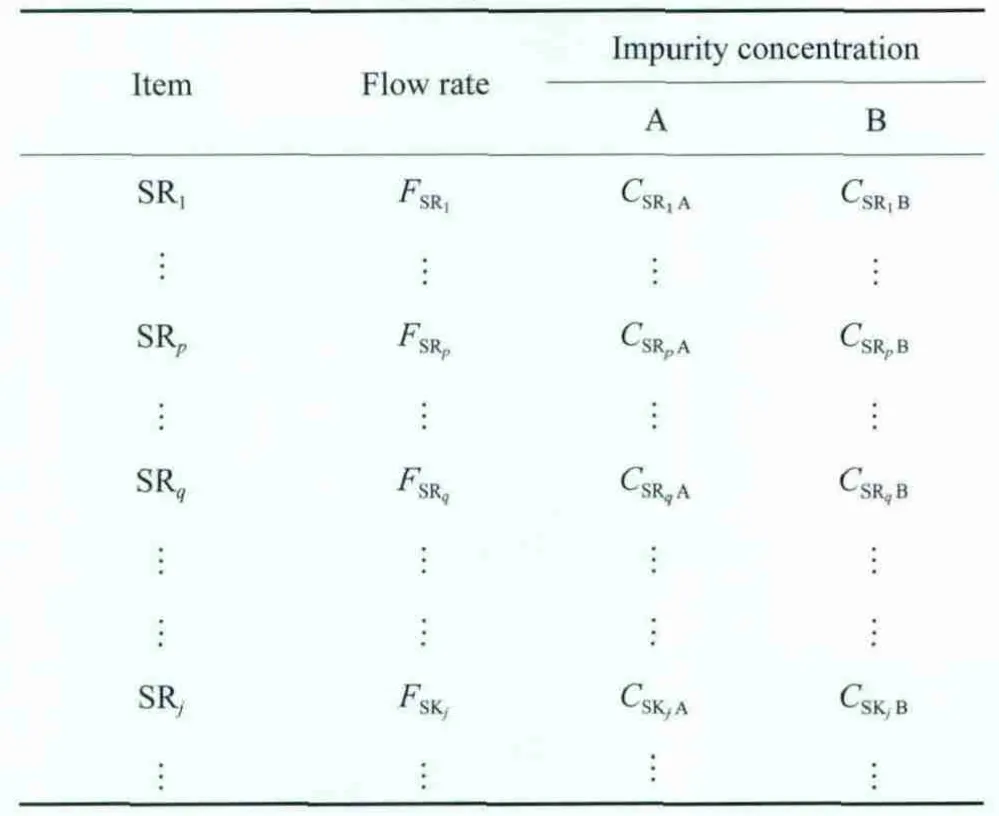
表3 复杂氢网络的氢源、氢阱数据Table 3 Data of hydrogen sources and hydrogen sinks for complex hydrogen network

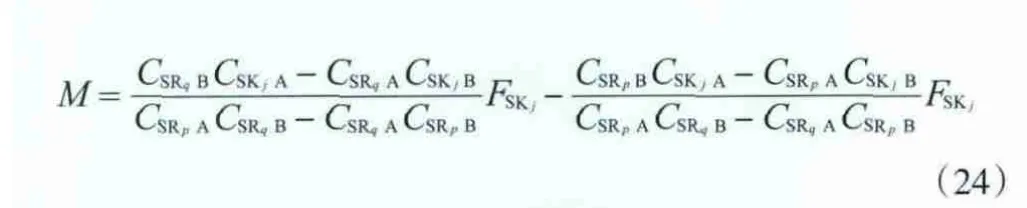
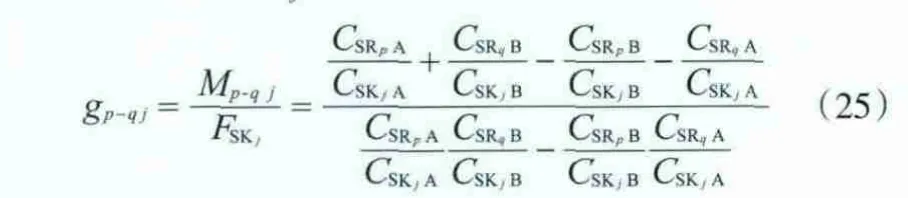
对于一个氢阱，当0＜ gp-qj＜1时，SRp和SRq混合互补后的总流量小于氢阱SKj需要的流量；当gp-qj=1时，SRp和SRq混合互补后的总流量等于氢阱SKj需要的流量；当gp-qj＞1时，SRp和SRq混合互补后的总流量大于氢阱SKj需要的流量。

比较gp-qj值可直接确定与该氢阱匹配的一组最佳混合互补氢源。将相应的氢源数据代入式（20）和式（21）即得到最优混合互补匹配结果。

当3个氢源对某氢阱同时参与混合互补时，需求解三元一次方程组。如对于表4所示的氢网络，Liu等［16］通过计算化简得到的匹配结果见式（26）～（28）。

表4 含3个氢源的三杂质氢网络数据Table 4 Data of hydrogen network with three hydrogen sources and three imprities

式中，P1，P2，P3分别为SRp，SRq，SRr对SKj的匹配流量；d1，d2，d3分别为氢阱SKj中杂质A，B，C的负荷：

对于式（26）～（28），代入计算仍十分繁杂，可做出一定的简化。经分析计算，可得到以下3个算式来判定匹配量：

以上3个算式中所有的比值都已在求解关键杂质时所用的比矩阵中算得，因此可直接代入求解。与式（26）～（28）相比，式（30）～（32）简化了一半以上的计算步骤。

若式（30）～（32）的计算结果中任何一个为负值，则3个氢源不能进行混合互补，停止计算；若式（30）～（32）的计算结果均大于0，计算gp-q-rj=gpj+gqj+grj，然后与判定两个氢源混合互补的g值统一起来比较，取g值最大的一组混合互补氢源进行匹配。

4 案例分析

某石化企业氢网络有6股氢源、6股氢阱，公用工程为纯氢，具体数据见表5。

采用现行矩阵法求解，可依次得到其M矩阵、P矩阵和O矩阵：

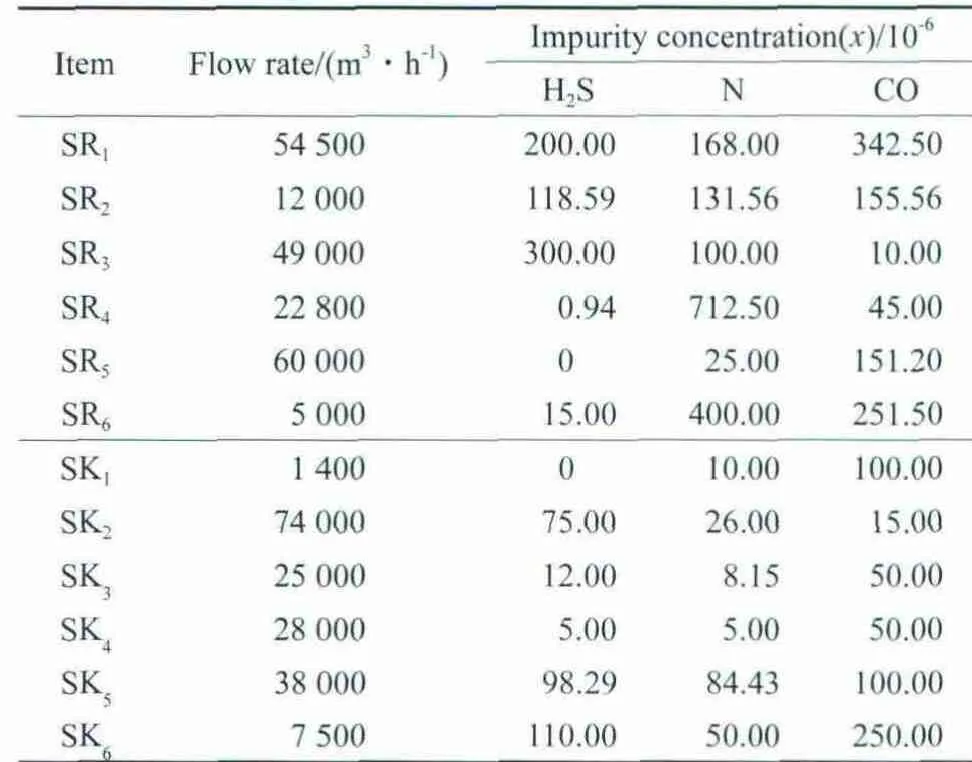
表5 某石化企业氢网络的氢源、氢阱数据Table 5 Data of hydrogen sources and hydrogen sinks from the hydrogen network of a petrochemical plant

在M矩阵中，各元素后的括号内给出了相应匹配的关键杂质。P矩阵是在根据M矩阵求解了30多个方程组和相应的不等式后得到的。根据O矩阵可得，整个氢网络回用氢量为98 055.57 m3/h，最小公用工程消耗量为81 244.43 m3/h。

采用本工作提出的改进矩阵法对表5所示的氢网络进行优化，对于氢阱SK2，求得的氢源与氢阱的杂质浓度比矩阵如下（矩阵中的*表示对应的杂质为关键杂质）：

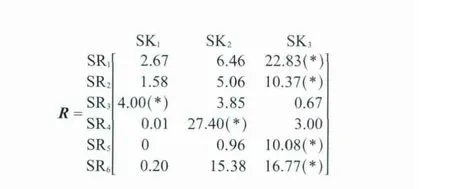
由R矩阵可见，共有9对氢源与SK2匹配时有混合互补的可能，具体如表6所示。对于SR1和SR4，它们分别与SK2匹配时的关键杂质分别为CO和N，这两个氢源中H2S的浓度与氢阱中H2S的浓度之比均小于其他杂质（N和CO）与氢阱SK2中相应杂质的浓度比，故这两个氢源混合互补时的关键杂质不变。同理，SR2和SR4、SR4和SR5以及SR4和SR6混合互补时的关键杂质也不变。而其他5对氢源混合互补时的关键杂质则有可能变化。因此，只需计算其他5对氢源的f值。

根据式（23）计算各对氢源的f值，计算结果列于表6。

表6 可与SK2匹配的混合互补氢源Table 6 Mixed complementary hydrogen sources matched with SK2

由表6可看出，SR1，SR2，SR5，SR6分别和SR3混合互补时f值为正，说明关键杂质会发生变化；而SR4和SR3混合互补时f值为负，说明关键杂质不发生变化。这些氢源混合互补后的关键杂质见表6。据此，可根据式（25）计算各组氢源的g值，计算结果列于表6。比较g值可见，SR3和SR5混合互补时对应的g值最大，这两个氢源混合与SK2匹配的流量最大，为23 867.3 m3/h。

对于SK5，存在3个氢源之间的混合互补情况，通过计算得到各组可能的混合互补氢源的g值，列于表7。

表7 可与SK5匹配的混合互补氢源Table 7 Mixed complementary hydrogen sources matched with SK5

按此混合互补计算步骤，可得到其他几个氢阱的匹配。最后得到的P矩阵和O矩阵如下：

优化后，系统的回用氢量为103 320 m3/h，最小公用工程消耗量为75 980 m3/h，后者比现行矩阵法的优化结果减少了5 264.43 m3/h。

5 结论

1）现行矩阵法的混合互补规则未考虑氢源混合后与氢阱匹配的关键杂质发生改变的情况，使得判断和计算结果不够准确。

2）提出了判断混合互补后关键杂质是否改变的参数f和判断方法，改进了现行矩阵法的混合互补判定规则。

3）提出了可比较各混合互补氢源与氢阱匹配流量大小的参数g，据此可容易地比较各混合互补氢源与氢阱的匹配流量大小，便于潜在匹配氢源和潜在匹配流量的确定。

4）以改进的矩阵法对某石化企业的氢网络进行优化，所得结果优于现行矩阵法。计算过程也证明改进后的混合互补判定规则更严谨，利用参数f和参数g进行优化的方法简单、方便、可行。

符 号 说 明

CSKjk氢阱SKj进口杂质k的摩尔分数，%

CSRpKIqj氢源SRp中关键杂质KIqj的摩尔分数，%

CSRpKIpj氢源SRp中关键杂质KIpj的摩尔分数，%

CSRqKIqj氢源SRq中关键杂质KIqj的摩尔分数，%

CSRqKIpj氢源SRq中关键杂质KIpj的摩尔分数，%

CSRik氢源SRi中杂质k的摩尔分数，%

FSKj氢阱SKj的流量，m3/h

FSRi氢源SRi的流量，m3/h

fp-qj判定混合互补后关键杂质是否变化的参数，无量纲

gp-qj氢源与源阱匹配程度的度量，无量纲

k 杂质种类

KI 关键杂质

Mij氢源SRi与氢阱SKj的最大匹配流量，m3/h

MPijk氢源SRi与氢阱SKj对应于杂质k的最大匹配流量，m3/h

M′SRpj潜在匹配氢源SRp混合后与氢阱SKj的匹配流量， m3/h

M′SRqj潜在匹配源SRq混合后与氢阱SKj的匹配流量， m3/h

m 氢源总数

n 氢阱总数

nc杂质总数

Oij氢源SRi与氢阱SKj的最佳匹配流量，m3/h

Pij氢源SRi与氢阱SKj的潜在匹配流量，m3/h

SK 氢阱

SR 氢源

［1］ Alves J J. Analysis and Design of Refinery Hydrogen Distribution Systems［D］. Manchesrer：UMIST，1999.

［2］ El-Halwagi M，Gabriel F，Harell D. Rigorous Graphical Targeting for Resource Conservation via Material Recycle/Reuse Networks［J］. Ind Eng Chem Res，2003，42（19）：4319 - 4328.

［3］ Zhao Zhenhui，Liu Guilian，Feng Xiao. New Graphical Method for the Integration of Hydrogen Distribution Systems［J］. Ind Eng Chem Res，2006，45（19） ：6512 - 6517.

［4］ Kazantzi V，El-Halwagi M M. Targeting Material Reuse via Property Integration［J］. Chem Eng Prog，2005，101（8） ：28 - 37.

［5］ Amutlaq A M，Kazantzi V，El-Halwagi M M. An Algebraic Approach to Targreting Waste Discharge and Impure Fresh Usage via Material Recycle/Reuse Networks［J］. Clean Technol Envir Policy，2005 ，7（4）：294 - 305.

［6］ Bandyopadhyay S. Source Composite Curve for Waste Reduction［J］. Chem Eng J，2006，125（2）：99 - 110.

［7］ Foo D C Y，Manan Z A. Setting the Minimum Utility Gas Flowrate Targets Using Cascade Analysis Technique［J］. Ind Eng Chem Res，2006，45（17）：5986 - 5995.

［8］ Hallale N，Liu Fang. Refinery Hydrogen Management for Clean Fuels Production［J］. Adv Environ Res，2001，6（1）：81 - 98.

［9］ Liao Zuwei，Wang Jingdai，Yang Yongrong，et al. Integrating Purifiers in Refinery Hydrogen Networks：A Retrofit Case Study［J］. J Cleaner Prod，2010，18（3）：233 - 241.

［10］ Liao Zuwei，Rong Gang，Wang Jingdai，et al. Rigorous Algorithmic Targeting Methods for Hydrogen Networks-PartⅠ：Systems with No Hydrogen Purification［J］. Chem Eng Sci，2011，66（5）：813 - 820.

［11］ Liao Zuwei，Rong Gang，Wang Jingdai，et al. Rigorous Aalgorithmic Targeting Methods for Hydrogen Networks-PartⅡ：Systems with One Hydrogen Purification Unit［J］. Chem Eng Sci，2011，66（5）：821 - 833.

［12］ Jeong C，Han Chonghui. Byproduct Hydrogen Network Design Using Pressure Swing Adsorption and Recycling Unit for the Petrochemical Complex［J］. Ind Eng Chem Res，2011，50（6）：3304 - 3311.

［13］ Jiao Yunqiang，Su Hongye，Hou Weifeng. Improved Optimization Methods for Refinery Hydrogen Network and Their Applications［J］. Control Eng Pract，2012，20（10）：1075 -1093.

［14］ Almansoonri A，Shah N. Design and Operation of a Future Hydrogen Supply Chain：Snapshot Model［J］. Chem Eng Res Des，2006，84（6）：423 - 438.

［15］ Zhou Li，Liao Zuwei，Wang Jingdai，et al. Hydrogen Sulfide Removal Process Embedded Optimization of Hydrogen Network［J］. Int J Hydrogen Energy，2012，37（23）：18163 -18174.

［16］ Liu Guilian，Tang Mingyuan，Feng Xiao，et al. Evolutionary Design Methodology for Resource Allocation Networks with Multiple Impurities［J］. Ind Eng Chem Res，2011，50（5）：2959 - 2970.

［17］ 刘桂莲，刘永彪，冯霄. 炼厂多杂质氢网络的集成［J］. 化工学报，2012，63（1）：161 - 167.

［18］ 刘桂莲，唐明元，冯霄. 多杂质氢网络的优化［J］. 石油化工，2009，38（4）：419 - 422.

［19］ 贾雪雪，刘桂莲. 多杂质氢网络矩阵优化法的改进［J］. 石油化工，2014，43（1）：30 - 36.