销轨弯曲角对采煤机行走机构动力学特性的影响

张　丹,　田　操,　孙月华,　任春平,　左胜甲

(1.黑龙江科技大学 机械工程学院, 哈尔滨 150022; 2.哈尔滨工程大学 机电工程学院, 哈尔滨 150001;3.东北农业大学 工程学院, 哈尔滨 150030)



销轨弯曲角对采煤机行走机构动力学特性的影响

张丹1,2,田操1,孙月华1,任春平1,左胜甲3

(1.黑龙江科技大学 机械工程学院, 哈尔滨 150022; 2.哈尔滨工程大学 机电工程学院, 哈尔滨 150001;3.东北农业大学 工程学院, 哈尔滨 150030)

为研究行走轮经过销轨连接处时的动力学特性,分析输送机在水平弯曲和垂直弯曲两种工况下销齿啮合中的三种激励,建立了销齿啮合力和导向滑靴与销轨间最小间隙的数学模型。利用ADAMS建立行走机构动力学仿真模型,模拟销轨间不存在弯曲角、存在水平弯曲角和存在垂直弯曲角三种状态的动力学特性。结果表明:销轨间不存在弯曲角时,行走轮角速度波动率为10.5%。随着弯曲角度的增大,行走轮角速度波动幅值由77 (°)/s增大到83 (°)/s,销齿啮合力幅值由504 kN增大至632 kN;而垂直弯曲角对行走轮速度波动不大,对销齿啮合力影响可忽略不计。该研究为行走轮与销齿的可靠性设计提供参考依据。

行走机构; 销轨弯曲角; 导向滑靴与齿轨间隙; 动力学特性

0　引　言

随着采煤机性能的不断提高,其装机功率已超过3 000 kW,整机牵引功率达400 kW,牵引力大于1 500 kN,行走轮模数达46.8 mm,销轨销齿节距为147 mm。随着整机功率的增大,行走部复杂的受力情况及恶劣的工作环境影响了行走机构的可靠性,使行走机构成为采煤机的主要故障部位[1]。行走机构一旦出现问题将严重降低采煤机工作效率,甚至导致其无法工作。国内学者对采煤机行走机构动态特性的研究取得了一定成果。王振乾分析了行走机构运动学特性,得出销轨连接处行走轮速度波动较大,销齿节距的变化对啮合的运动学特性影响显著[2]。王兴文分析了行走轮磨损及断齿原因,指出导向滑靴与销轨间隙过大和导向作用减弱是造成行走轮与销齿啮合不良的重要原因[3]。王淑平研究了大型采煤机滑靴的磨损机理,得出由于输送机水平弯曲角及垂直弯曲角的存在,增大了滑靴与销轨相对运动的摩擦力,加剧滑靴的摩擦磨损[4]。由于输送机的弯曲角度对销轨连接处的结构有重要影响,而行走轮在销轨连接处的动态特性直接关系到采煤机工作的稳定性和可靠性。因此,笔者采用虚拟样机技术研究输送机水平弯曲角及垂直弯曲角对行走机构动态特性的影响。

1　采煤机行走机构传动原理

行走机构工作原理如图1所示。行走机构的输入轴经过图1所示齿轮1与惰轮啮合,向下传递给齿轮2,齿轮2与行走轮通过花键连接,最后行走轮轮齿和刮板运输机上销轨的销齿啮合,推动采煤机前进。安装在行走轮轴上的导向滑靴引导采煤机行走,从而保证行走轮与销轨销齿正常啮合。销齿啮合过程类似于齿轮齿条啮合过程,为适应底板的不平整以及输送机的弯曲,齿轨间采用元宝座连接,且要允许齿轨连接处水平与垂直方向都存在一定的弯曲角度,使齿轨的节距不断变化,导致行走轮在经过齿轨连接处受到冲击载荷。

图1　行走机构传动原理

2　销齿传动的啮合力

销齿传动过程类似于齿轮齿条传动过程,行走机构除了受到外部的振动激励外,在啮合过程中也会产生内部的动态激励。动态激励是系统振动的根源,主要包括刚度激励、啮合冲击激励和误差激励。

2.1刚度激励

如果把销齿副看作沿啮合线方向的弹簧,弹簧刚度的变化必然引起啮合力的变化。刚度激励是由于啮合过程中重合度变化引起的,增大重合度可以提高啮合刚度。一般情况下,销齿传动的重合度1≤ε≤2。当销齿法向节距小于行走轮法向节距时,啮合重合度小于1,在啮合过程中一对齿与两对齿交替啮合,销齿传动的综合啮合刚度kv可表示为

kv=∑kvi(i=1,2),

(1)

式中:kvi——第i对销齿的综合啮合刚度;

k1i——行走轮啮合点法向的啮合刚度;

k2i——销齿啮合点法向的啮合刚度。

此时,系统对应的阻尼为综合啮合阻尼,用cvi表示。由于k1、k2是啮合点位置的函数,因此,齿对i的综合啮合刚度也是齿对啮合位置的函数。两对销齿啮合刚度的变化如图2所示。图2中Δt为一对轮齿啮合时间。实际进行分析时,将此曲线简化为矩形波。

图2　两对轮齿啮合刚度

2.2啮合冲击激励

行走轮制造过程中产生的基节误差和销齿啮合时的弹性变形会产生啮合冲击。销齿在啮入、啮出都会产生冲击,啮合冲击属于瞬间行为,是一种动态载荷激励,用常规方法很难定量确定啮合冲击激励f(t)。文中利用文献[5]通过有限元方法模拟齿轮传动内部的啮合冲击激励近似代替。

2.3误差激励

误差激励主要是由行走轮以及齿轨的几何误差引起的,包括加工误差和装配误差。由于采煤机行走部为开式传动系统,在传动过程中,行走轮与齿轨之间夹杂大量煤粉与煤块,销齿啮合处接触精度不高,因此,误差激励不容忽视。它是一种位移激励,与接触点处弹性变形量有关,其转角长周期误差为一近似正弦曲线，如图3所示,短期误差可用傅里叶级数表示[6]

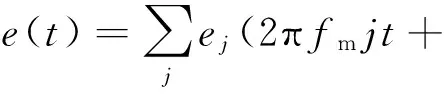
式中:ej——第j阶分量的幅值;

φj——第j阶分量的相位;

fm——啮合频率。

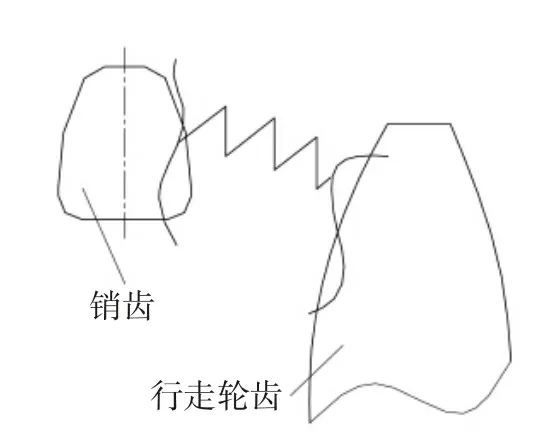
图3　误差激励

2.4销齿传动的啮合力

销齿传动中,第i个齿对在啮合点处的法向啮合力Fi为

Fi=kviδi,

(2)

式中:δi——齿对i在啮合点位置的综合变形,其值与齿部的弯曲与剪切变形、齿根弹性引起的附加变形及啮合点的接触变形有关[6]。

用ei表示第i对齿的齿廓误差,则δi=θrd-x1-ei。销齿动态啮合的啮合力可表示为

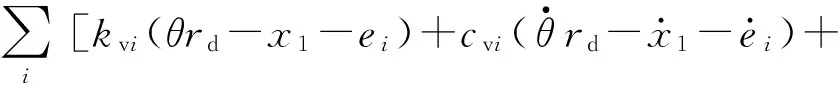
f(t)],i=1,2,

(3)

式中:θ——行走轮转角,rad;

cvi——行走轮轴沿牵引方向振动位移,mm;

rd——行走轮基圆半径,mm。

3　导向滑靴与销轨的结构关系

3.1销轨间的弯曲角

为了适应底板起伏不平及输送机移溜,允许输送机在垂直方向有±3°和水平方向有±1°的弯曲角度[7],根据输送机与销轨的结构及尺寸关系可知,销轨在垂直方向和水平方向允许的弯曲角度，分别为±1.5°和±0.5°。销轨间的垂直弯曲角度,会造成销轨连接处销齿节距的变化,致使销齿啮合不良。销轨间水平弯曲角度,会造成行走轮与销齿形成点接触,降低销齿啮合的承载力[8]。

3.2导向滑靴与销轨的最小间隙

导向滑靴起支撑采煤机并引导采煤机行走轮沿着销轨正确行走的作用。由于销轨间弯曲角的存在,为保证导向滑靴顺利通过两节销轨连接处,导向滑靴与销轨之间必须设置一定的间隙。间隙大小对采煤机行走机构的性能有重要影响。间隙过小,导向滑靴和销轨可能会产生干涉,导致滑靴掰断或卡死;间隙过大,会降低导向作用,当行走轮受到偏载时,会严重恶化行走轮与销齿的啮合[9]。导向滑靴和销轨侧面之间的最小间隙由导向滑靴的长度、销轨的宽度及弯曲角决定。图4为导向滑靴长度方向中点通过两节销轨连接处的位置图,分析易得最小间隙cmin及导向滑靴最小宽度bmin分别为

cmin=bmin-b0,

(4)

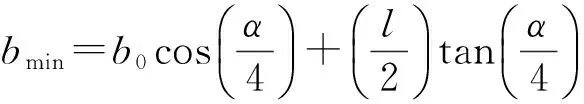
(5)

式中:b0——销轨宽度,mm;

l——导向滑靴长度,mm;

α——输送机允许的水平弯曲角度,α/4即为单节销排的最大弯曲角,(°)。

将式(4)、(5)联立,得

(6)

图4　导向滑靴与销排位置关系

同理,可知导向滑靴与销轨垂直方向的最小间隙为

(7)

式中:h0——销轨的高度,mm;

β——输送机允许的垂直弯曲角度,(°)。

4　行走机构动力学仿真

4.1仿真模型

以某型号采煤机为例,其配套销轨为147销轨。运用ADAMS软件对建立的虚拟样机进行静力、动力学分析。将在PRO/E中建立好的三维模型通过接口文件导入到ADAMS/View中,把不参与运动及不影响运动的部件删除,虚拟样机仿真模型如图5所示。

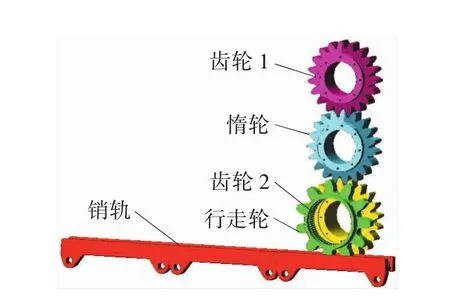
图5　行走部仿真模型

4.2参数设置

某型号采煤机,其牵引电机转速为1 472 r/min,经二级行星减速器进行减速,计算得到图5所示齿轮1的转速,以此作为输入转速。最大牵引力为1 000 kN,将施加在行走机构的牵引负载转化为行走轮上的负载转矩,负载由两个行走机构共同承担。一般使用两种信号模拟牵引负载,正常工况下的正弦信号和遇到夹矸工况的阶跃信号。为研究销轨间弯曲角对行走机构动态特性的影响,使用正弦信号模拟牵引负载[10-11]。行走轮和销轨间设置接触力;齿轮2与行走轮之间施加扭簧,其刚度定义如下[12]:

(8)

式中:T——作用在弹性轴段上的扭矩,N·m;

φ——弹性轴段在扭矩T作用下的变形角度,rad;

E——材料的剪切弹性模量,Pa;

IP——弹性元件的极惯性矩,m4;

L——弹性轴段的长度,m。

计算得行走部各施加构件载荷,齿轮2与行走轮之间扭簧刚度k=7.3N/m、齿轮1与驱动力矩M1=300 (°)/s、行走轮牵引力负载转矩M2=120 900N·m,以销轨间水平弯曲角及垂直弯曲角作为变量,设置仿真时间2s,仿真步长为600,进行仿真计算。

5　仿真结果与分析

销轨间销齿节距大于标准节距,且不存在弯曲角时,以节距149mm为例,行走轮角速度ω波动曲线如图6所示,销齿啮合力如图7所示。

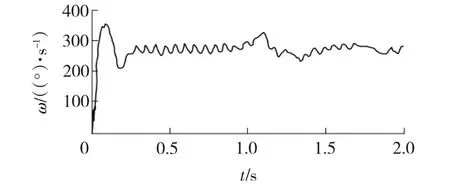
图6　行走轮角速度曲线

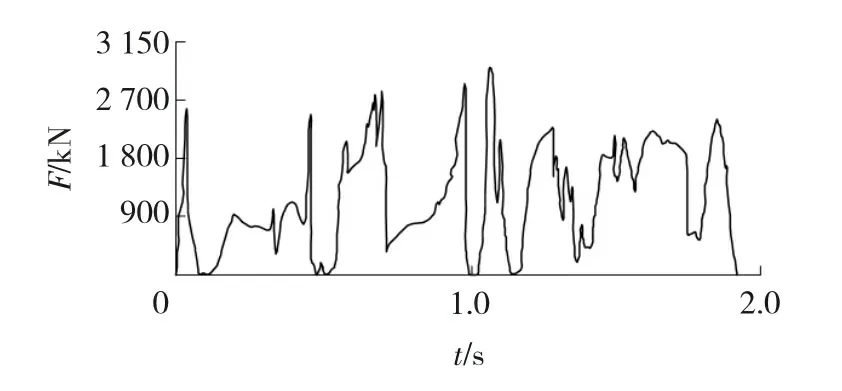
图7　销齿啮合力曲线

由图6～7可见:行走轮角速度在初始阶段由于碰撞冲击出现峰值,角速度波动十分大,之后基本稳定。当行走轮运动到销轨连接处时,由于销齿节距发生变化,其速度出现较大波动,但很快稳定。最大波动值出现在初始阶段,即电机启动后瞬间,角速度最大值与角速度均值之间的波动幅值为71 (°)/s,稳定运行后,其波动幅值为40 (°)/s,平均速度波动率为10.5%。由图7可见,由于销齿啮合位置的变化,销齿啮合力同样产生剧烈变化。销齿啮合力均值为382kN,最大啮合力与啮合力均值间的啮合力幅值为408kN,出现在销轨连接处,销齿啮合力多次出现零值,说明销齿与行走轮多次发生分离,这是销轨与行走轮多次产生碰撞冲击的结果。

根据均匀设计实验法的基本理论,假设实验点在实验范围内均匀分布。调整仿真模型,设置销轨间销齿节距为147mm,旋转销轨,使销轨间可以水平弯曲0.25°、0.5°,垂直弯曲0.5°、1°、1.5°,仿真得到不同角度时行走轮速度波动幅值和销齿啮合力幅值，如表1所示。行走轮角速度曲线如图8所示, 销齿啮合力曲线如图9所示。

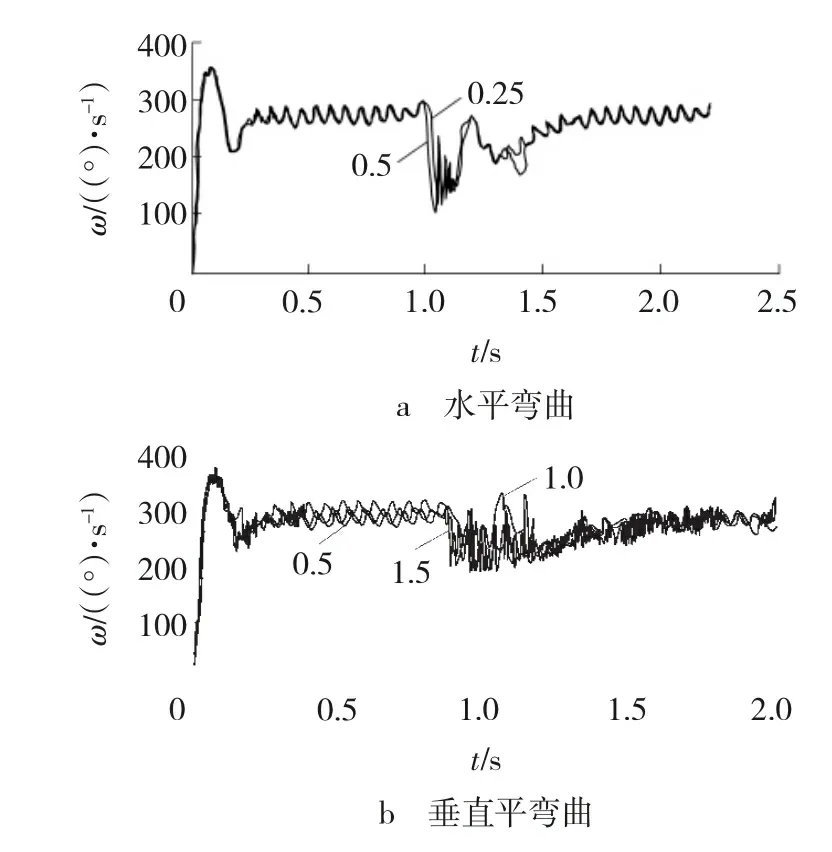
图8　行走轮角速度曲线

图9　销齿啮合力曲线

由表1可知,当销轨间存在弯曲角度时,行走轮速度波动幅值ω和销齿啮合力幅值F均出现在销轨连接处,因为销轨连接处节距的变化导致了啮合状态的瞬间变化。因此,行走轮速度波动幅值和销齿啮合力幅值都相应增加,且随着弯曲角度的增大而增大。在销齿啮合过程中,销齿啮合力不但出现零值,而且多次出现负值,说明在行走轮此时销齿啮合不但产生了分离,而且出现了齿背啮合的状况,此时,牵引负载只能由另一个行走轮承受。可见,在水平弯曲角下销齿啮合受较大冲击,这种往复的冲击极易造成行走轮的疲劳断裂或强度不足而断裂。而且,水平弯曲角不但使行走轮角速度波动幅值明显提高,也会显著提高销齿啮合力的幅值。由于销齿啮合反复接触,会严重降低行走轮及销齿的疲劳寿命。此时,销齿啮合形成了点接触,这与实际状况相符,也与文献[2]、[13]、[14]研究结论一致。销轨间的垂直弯曲角对行走轮角速度波动幅值有一定影响,但对销齿啮合力影响不大,这是因为,垂直弯曲时销齿啮合只是节距发生了变化,使行走轮速度产生了一定波动,但销齿啮合仍然是线接触,销齿啮合位置变化不明显。

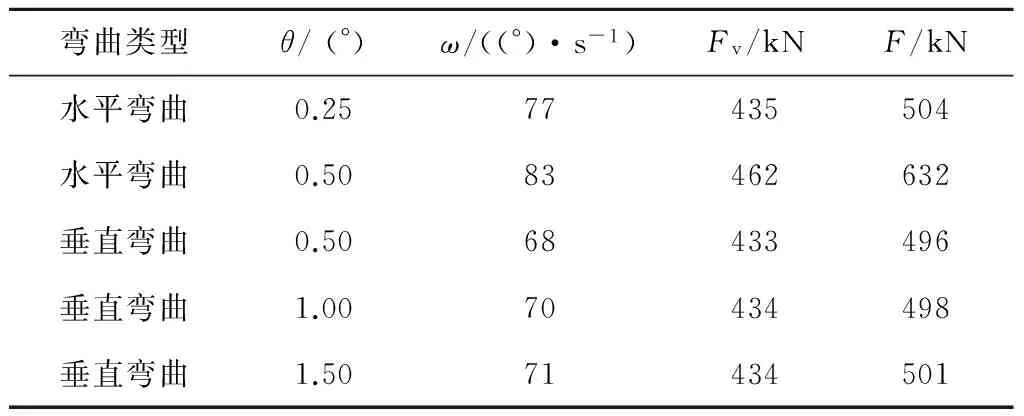
表1　不同弯曲角下行走轮速度波动幅值和销齿啮合力幅值

6　结　论

(1)将销齿啮合的内部激励分为刚度激励、啮合冲击激励和误差激励,啮合刚度是齿对啮合位置的函数,啮合冲击激励是一种动态误差激励,得出误差激励主要由行走轮及销轨几何误差引起,给出了各激励和销齿啮合力的计算方法。

(2)根据输送机及销轨之间的结构及尺寸关系,计算了导向滑靴与销轨之间的最小间隙,得出最小间隙与导向滑靴长度、输送机弯曲角及销轨宽度和高度有关,增大导向滑靴长度,可以提高支撑能力,为不与销轨产生干涉,需适当增大间隙,此时,滑靴导向能力会降低。

(3)销轨间存在弯曲角时,销齿啮合存在齿背啮合的状况。此时,牵引负载只能由另一个行走轮承受。销轨间的垂直弯曲角对销齿啮合力影响不大,但对行走轮角速度波动幅值影响较大。随着销轨间的水平弯曲角的增大,行走轮角速度波动幅值与销齿啮合力幅值均显著提高。

(4)若不考虑牵引负载特性,造成行走轮波动的主要原因是初始冲击、轮齿与销齿非共轭啮合及销轨之间的不平滑连接,为改善行走机构动态特性,需要在齿轮齿廓设计及结构设计上进行改进。

[1]刘春生, 闫晓林. 国内大功率自动化电牵引采煤机的现状和发展[J]. 煤矿机电, 2003(5): 39-42.

[2]王振乾. 滚筒式采煤机行走机构运动学分析及强度研究[D]. 上海: 煤炭科学研究总院, 2007.

[3]王兴文, 张勇涛, 李英, 等. 采煤机行走部齿轮磨损的原因分析及预防措施[J]. 煤矿机械, 2013, 34(3): 195-196.

[4]王淑平, 杨兆建. 大型采煤机滑靴磨损机理分析[J]. 煤矿机械, 2010, 31(9): 71-73.

[5]李润方, 陶泽光, 林腾蛟, 等.齿轮啮合内部动态激励数值模拟[J]. 机械传动, 2001, 25(2): 1-3.

[6]张策. 机械动力学[M]. 2版. 北京： 高等教育出版社, 2008.

[7]刘春生, 王旭东. 采煤机牵引导向滑靴配合间隙设计[J]. 煤矿机械, 2005(10): 4-5.

[8]刘占胜, 马英. 采煤机行走机构与刮板输送机销轨啮合配套研究[J]. 煤矿机械, 2007, 28(7): 30-32.

[9]李德根, 刘春生. 镐型截齿截割煤岩动力系统的混沌特征[J]. 黑龙江科技学院学报, 2011, 21(6): 458-462.

[10]ZHANG DAN, HU SHENGHAI, LIU CHUNSHENG, et al. Modeling and kinematics simulation of shearer’s travelling mechanism based on virtual prototyping technology[J]. Advanced Materials Research, 2013, 22(3); 396-399.

[11]刘春生， 任春平， 李德根. 修正离散正则化算法的裁割煤炭载荷谱的重构与推演[J]. 煤炭学报， 2014， 39(5)： 981-986.[12]周甲伟, 刘瑜, 刘送永, 等. 采煤机行走机构动态啮合特性分析[J]. 工程设计学报, 2013, 20(3): 230-235.

[13]郎国军, 苑雪涛, 庹文敏, 等. 采煤机行走轮断齿现象分析[J]. 煤矿机电, 2010(3): 34-35.

[14]宋欣颖. 采煤机行走轮疲劳寿命仿真研究[J]. 机械设计与制造, 2013, 15(5): 249-251.

[15]杨大兵， 常光伟， 刘刚. 运输顺槽转角、四风顺槽一次性延面研究[J]. 河北工程大学学报： 自然科学版， 2008， 35(2)： 79-81.

(编辑李德根)

Effect of bending angle of conveyor on dynamics of shearer running gear

ZHANGDan1,2,TIANCao1,SUNYuehua1,RENChunping1,ZUOShengjia3

(1.School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China; 2.College of Mechanical & Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 3.School of Engineering, Northeast Agricultural University, Harbin 150030, China)

This paper is concerned with an insight into the dynamic behaviour of a walking wheel going through the connection of pin rails. The research consists of analyzing three kinds of incentives of pin teeth meshing in both the horizontal bending and the vertical bending of the conveyor and developing the two mathematical models, one for pin tooth meshing force and the other for the minimum gap between the guide shoes and pin rail. The study goes further into the development of the dynamic model of walking mechanism using the software ADAMS and the subsequent simulation of the dynamic dynamic characteristics of the following three statuses between pin rails: the absence of bending angle, the presence of horizontal bending angle and vertical bending angle. The result indicates that the absence of bending angle between pin rails means the angular velocity fluctuations of walking wheel of 10.5%; the increasing bending angle affords an increase from 77 (°)/s to 83 (°)/s in the angular velocity fluctuations amplitude of walking wheel and an increase from 504 kN to 632 kN in pin meshing force amplitude; the vertical bending angle has little impact on walking wheel velocity fluctuation, meaning that its impact on pin tooth meshing force is negligible. The study provides a reference for the reliability design of walking wheel and pin teeth.

walking mechanism; bending angle of the conveyor; guide shoes and pin rail gap; dynamic characteristics

2014-02-10

黑龙江省教育厅科学技术研究项目(12531006)

张丹(1982-),女,黑龙江省哈尔滨人,讲师,博士研究生,研究方向:多刚体动力学仿真,E-mail:bishe-2006@163.com。

10.3969/j.issn.2095-7262.2014.03.009

TD421.6

2095-7262(2014)03-0262-05

A