冲击载荷下不同有效长度扭矩轴的扭转特性
2014-11-03刘春生鲁士铂张艳军
刘春生, 鲁士铂, 张艳军, 王 甜
(黑龙江科技大学 机械工程学院, 哈尔滨 150022)
冲击载荷下不同有效长度扭矩轴的扭转特性
刘春生,鲁士铂,张艳军,王甜
(黑龙江科技大学 机械工程学院, 哈尔滨 150022)
为研究扭矩轴的有效长度和载荷对其扭转特性的影响,应用ANSYS Workbench有限元软件,当扭矩轴的卸荷槽尺寸不变、有效长度967~267 mm和载荷瞬态冲击时间0.005~0.100 s时,分析扭矩轴扭转过程的静力学和瞬态动力学特性。结果表明:在不同瞬态冲击时间下,扭矩轴的切应力变化与弹塑性变形过程存在明显差异;扭矩轴有效长度越小,切应力越大;当瞬态冲击时间为0.005 s时,切应力的平均变化率为5.6 MPa/dm,瞬态冲击时间越短,切应力越大且梯度变化越大,呈现非线性特征;当有效长度为267 mm时,0.005 s切应力最大变化大于27 MPa。该研究可为扭矩轴的结构设计提供参考依据。
采煤机; 扭矩轴; 有效长度; 瞬态冲击时间; 切应力
扭矩轴通过两端的渐开线花键将机械传动系统与驱动电机连接起来,传递动力。当采煤机处于严重超载运行时,为保护其他传动件不因载荷过大而损坏,扭矩轴首先发生断裂,使整个传动系统断开,起到过载保护的作用,扭矩轴是采煤机截割部传动系统的薄弱环节。在实际使用中,由于采煤机所受不确定的载荷,以及扭矩轴设计方法和制造工艺等原因,扭矩轴常发生严重过载而未及时断裂,有时过载负荷在允许范围内,扭矩轴出现扭断现象,导致其不能有效起到过载保护和可靠传递动力的作用[1-3]。因此,笔者研究在不同载荷瞬态冲击时间和扭矩轴不同有长度下扭矩轴的动力特性,以改进扭矩轴的设计方法,提高采煤机的可靠性和使用寿命。
1 结构参数
采煤机扭矩轴的结构形式,如图1所示。扭矩轴结构长度L=1 204 mm、D=70 mm、有效扭转长度l=967 mm、U型卸荷槽外径d=55 mm、圆弧半径r=5 mm,以及内径d0=35 mm。截割电机额定功率P=500 kW、额定转速n=1 480 r/min和电机额定转矩TH=3.209×103N·m。
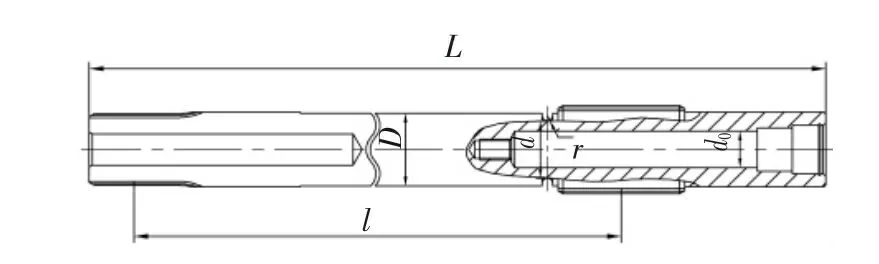
图1 扭矩轴结构
抗扭截面模量:
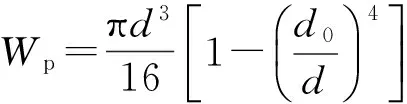
(1)
扭矩轴的静强度安全系数:
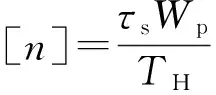
(2)
扭矩轴设计时安全系数[n]=2.5,将扭矩轴的参数代入式(1),求得抗扭截面模量Wp=2.72×10-5m3。由式(2)推算出,扭矩轴材料剪切屈服极限τs=300 MPa。
2 有限元模型
采用Pro/E三维绘图软件对扭矩轴进行建模,利用ANSYS Workbench仿真功能,通过数据交换接口将扭矩轴模型数据导入ANSYS Workbench中,模型参数传递过程没有元素丢失。建模中根据扭矩轴的工作特点,在保持其力学性能不变的条件下,对扭矩轴的结构进行适当简化,如将花键轴简化为圆柱体、不考虑轴外表面倒角等,只考虑对扭矩轴性能影响的主要结构部分[4]。
2.1破坏准则
扭矩轴的材料为40Cr、抗拉强度σb=750MPa、抗拉屈服极限σs=550MPa、机械手册中推荐的剪切屈服极限τs=(0.55~0.62)σs=303~341MPa,剪切强度τb=(0.55~0.62)σb=412.5~465MPa。扭矩轴的破坏形式有两种。一种是当扭矩轴受扭时,所受到的切应力τ介于τs和τb之间,扭矩轴发生不可逆的塑型变形,此时,扭矩轴虽然没有发生断裂,但也可认为是一种失效形式。另一种是当扭矩轴所受到的切应力大于剪切强度时,即τ>τb时,扭矩轴发生断裂,使截割部的传动系统断开。
2.2网格划分
在ANSYSWorkbench中设置材料的弹性模量2.1×105MPa、泊松比0.277。为了提高计算效率,保证分析结果更加精确,采用四面体划分网格,网格生长方式为PatchConforming,并对U型卸荷槽部分进行局部细化[5]。通过Mesh工具栏插入局部尺寸控制,网格划分结果,如图2所示。扭矩轴网格划分的节点总数为26 404个,单元总数为15 361个。

图2 扭矩轴的网格划分
3 力学分析
3.1静力学
通过Staticstructural模块对扭矩轴进行静力学分析,如图3a所示。按[n]=2.5倍驱动电机额定转矩加载,即在扭矩轴的B面上施加转矩[n]TH=8.022×103N·m,将与电机配合的整个渐开线花键的分度圆环面A上添加固定约束。经求解可得扭矩轴的最大切应力云图如图3b所示,径向位移云图如图3c所示。

图3 扭矩轴静态分析
在扭矩轴受扭过程中,材料处于纯剪切状态。从图3b中可以看出,扭矩轴的应力集中在U型卸荷槽处,最大切应力为336.5MPa,超出理论推算的材料剪切屈服极限τs=300MPa(材料手册推荐的剪切屈服极限τs=303~341MPa),理论上扭矩轴已经发生塑性变形。由图3c可见,扭矩轴的扭转最大位移在轴的底部,扭转角为2.2°(理论计算扭转角为2.305 1°)。
3.2瞬态动力学分析
扭矩轴的设计方法通常采用静强度设计准则[6],由于采煤机在实际工作的过程中,截割部受力复杂,滚筒的载荷波动范围比较大,是一种瞬态的动载过程。静强度方法设计不能满足扭矩轴的实际使用工况,有必要对扭矩轴进行瞬态动力学分析。模拟扭矩轴在冲击载荷下的受力情况,考察冲击载荷梯度的影响程度,以确定扭矩轴在瞬态冲击作用下所受到的切应力。根据牛顿第二定律和达朗贝尔原理,得到扭矩轴受到冲击过程的瞬态动力学方程:

式中:M──系统的质量矩阵;
K——系统的刚度矩阵;

F(t)——系统瞬态冲击载荷;
C——实验确定的系统阻尼系数矩阵。
3.2.1载荷瞬态冲击时间
采煤机工作时,截齿切割到硫化铁结晶、坚硬的岩石或碰到液压支架之类的金属构件,产生过载闷车,采煤机滚筒会突然停止运转[7],此时滚筒受到的截割阻力相当于阶跃载荷。当截割阻力经过滚筒和齿轮系传递到扭矩轴时,形成了瞬态冲击时间很小的斜坡载荷。为了能够了解扭矩轴在不同瞬态冲击时间所受应力大小,分别选取0.005、0.010、0.050和0.100 s四种瞬态冲击时间进行加载。在轴的一端设定固定约束“Fixed Support”,另一端施加2.5倍电机额定转矩。
3.2.2扭矩轴的有效长度
为了确定扭矩轴的有效长度与最大切应力的关系,在不改变扭矩轴卸荷槽处尺寸及两端花键形式下,将扭矩轴的有效长度l按100 mm减小,有效长度分别为867、767、667、567、467、367和267 mm,对不同有效长度的扭矩轴进行瞬态动力学分析。
4 结果与分析
经求解,得到扭矩轴在U型卸荷槽处的时间—切应力变化曲线,图4为有效长度l2=967mm和l1=267mm的扭矩轴在四种不同瞬态冲击时间下的切应力曲线,扭矩轴经过弹性阶段、屈服阶段、强化阶段产生塑性变形[8]。以图4c的0.05s冲击时间为例,扭矩轴在受扭的过程中,随着扭矩的不断增大,首先经过弹性阶段OA直线段,在这一阶段中,材料服从切变虎克定律,即材料的切应力τ与切应变成正比[9]。在屈服阶段AB曲线段,当屈服阶段图形为锯齿形状时,切应力首次下降前为上屈服切应力,而在屈服阶段中最小应力为下屈服切应力,随后扭矩轴进入强化阶段BC曲线段。
从图4可以看出,在四种不同瞬态冲击时间下,l1=267mm的扭矩轴所受到的切应力均大于l2=967mm的扭矩轴。在图4a中,当瞬态冲击时间为0.005s时,长度为967mm的扭矩轴在5.41×10-3s时出现了波峰,U型卸荷槽处所受到的切应力τ=363.63MPa,长度为267mm的扭矩轴在5.29×10-3s时的最大切应力τmax=402.79MPa,均大于扭矩轴的剪切屈服极限τs,小于接近剪切强度τb,此时扭矩轴已失效,但并没有断裂。当瞬态冲击时间由0.005s增大到0.100s时,扭矩轴所受到的切应力逐渐减小。不同有效扭转长度的扭矩轴在四种瞬态冲击时间下所对应的切应力,如表1所示。
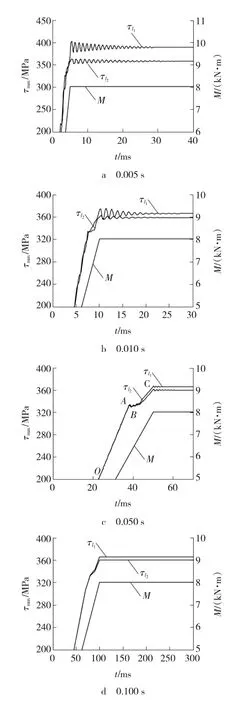
图4 不同瞬态冲击时间下扭矩轴的最大切应力曲线
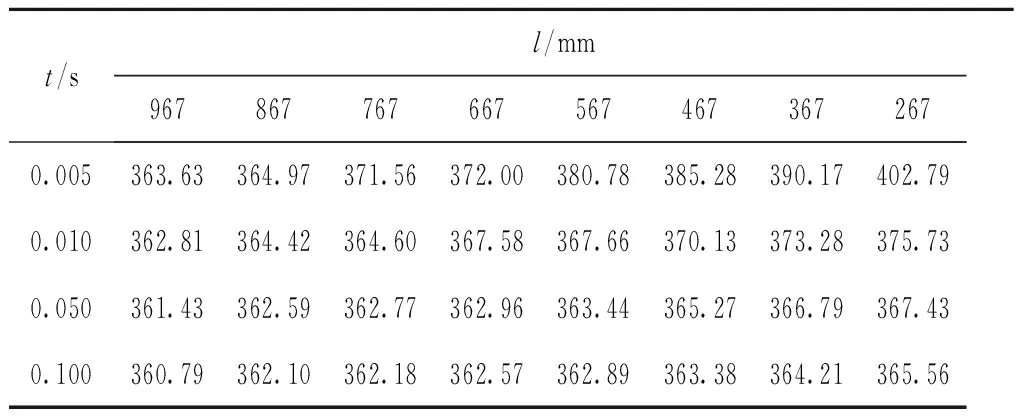
t/sl/mm9678677676675674673672670.005363.63364.97371.56372.00380.78385.28390.17402.790.010362.81364.42364.60367.58367.66370.13373.28375.730.050361.43362.59362.77362.96363.44365.27366.79367.430.100360.79362.10362.18362.57362.89363.38364.21365.56
由表1可知,在四种不同的瞬态冲击时间下,扭矩轴的长度l越小,切应力越大。当瞬态冲击时间为0.005 s,扭矩轴有效扭转长度l从967 mm减小到267 mm时,最大切应力增量为39 MPa,其单位长度平均变化率为5.6 MPa/dm。扭矩轴的有效长度减小,扭转刚度增大,冲击载荷效应越敏感,受到的切应力越大。当l为267 mm时,扭矩轴受到的切应力最大为402.79 MPa,载荷冲击时间从0.010 s减少到0.005 s时,最大切应力增量为27 MPa。显然,冲击时间越小,应力变化梯度越大,呈现出非线性特征。
将表1的数据应用MATLAB软件拟合,得出四种不同瞬态冲击时间下,扭矩轴的有效长度—切应力变化曲线,如图5所示。
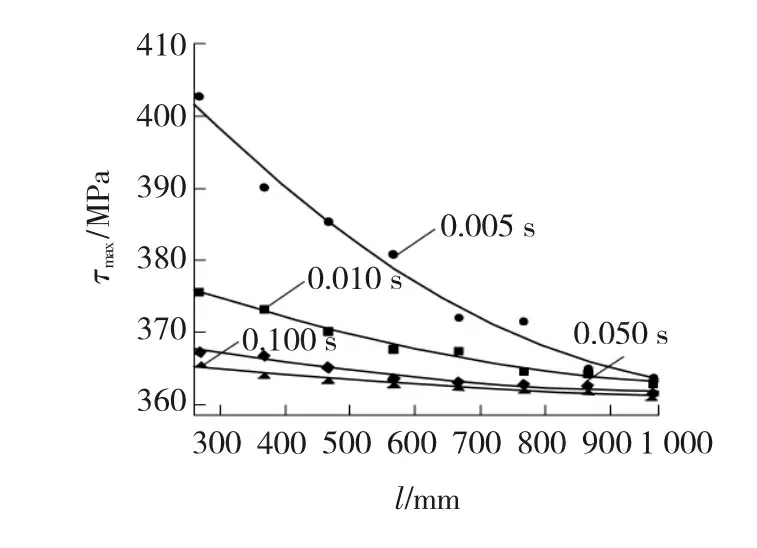
图5 不同瞬态冲击时间与扭矩轴有效长度所对应的切应力曲线
Fig. 5Different transient torque shaft impact effective length of time and corresponding shear stress curve
从图5可以看出,当瞬态冲击时间由0.100 s减小到0.005 s时,l为967 mm的扭矩轴切应力由360.79 MPa增加到365.56 MPa,说明原扭矩轴在不同瞬态冲击时间下切应力变化不明显;对于l为267 mm的扭矩轴,切应力由362.89 MPa增加到402.79 MPa,有效扭转长度l越小,切应力随冲击时间变化范围越大。
5 结束语
静态分析与瞬态动力学分析结果表明,扭矩轴在受到载荷时,会在卸荷槽根部产生应力集中。在对扭矩轴施加大小相等的扭矩时,扭矩轴受到瞬态冲击时所产生的切应力大于静态分析所产生的切应力,因此,设计扭矩轴时,需要考虑扭矩轴的有效长度和冲击载荷梯度的大小。在扭矩轴的瞬态动力学分析中,瞬态冲击时间越短,扭矩轴所受到的切应力越大。扭矩轴的有效扭断长度不同,扭矩轴所受到的切应力也不同,长度越长,扭矩轴刚度越小,越抗扭,长度越短,扭矩轴刚度越大,越容易断裂。扭矩轴通常按τs准则和静强度设计方法,而在实际工况中,扭矩轴受到瞬态冲击载荷,因此,确定采煤机滚筒冲击载荷及等效传递到扭矩轴上的冲击载荷梯度与载荷幅值非常重要。
[1]陈建文, 浦国树, 王雅萍. 弹性扭矩轴的设计[J]. 煤矿机电, 1998(1): 35-36.
[2]刘春生, 靳立红, 闫晓林. 采煤机弹性扭矩轴功能设计[J]. 矿山机械, 2009, 37(9): 1-3.
[3]刘春生, 侯清泉. 采煤机弹性扭矩轴的动态分析及设计[J]. 煤矿机械, 2001(6): 1-3.
[4]赵丽娟, 周字. 基于ANSYS/LS-DYNA的薄煤层采煤机扭矩轴动力学接触分析[J]. 煤矿机械, 2009, 30(4): 68-70.
[5]ZHENG SONGLIN, XU HONGHUI, FENG JINZHI, et al. Lightweight design of automobile drive shaft based on the characteristics of low amplitude load strengthening[J]. CHINESE JOURNAL OF MECHANICAL ENGINEERING, 2011, 24(6): 1111-1115.
[6]吴卫东, 郭昌利. 采煤机摇臂转矩轴的有限元分析[J]. 机械传动, 2012, 36(4): 84-86.
[7]刘春生, 靳立红. 采煤机截割部双电机串联驱动系统[D]. 哈尔滨: 黑龙江科技学院, 2010.
[8]LIU GUANGLIAN, HUANG MINGHUI, TAN QING, et al. Analysis of complete plasticity assumption for solid circular shaft under pure torsion and calculation of shear stress[J]. J Cent South Univ Technol, 2011, 18(1): 1018-1023.
[9]孟宪红, 白曌宇, 张行. 扭杆刚度衰减加速试验的损伤力学分析[J]. 机械工程学报, 2007, 43(7): 44-48.
(编辑李德根)
Torsion characteristics of torque shaft with different effective lengths under loading impact
LIUChunsheng,LUShibo,ZHANGYanjun,WANGTian
(School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)
This paper is an effort to delve into the effect of effective length and loading on torsion characteristics on the torque shaft. The research uses ANSYS Workbench finite element software to analyze the characteristics of the torque shaft in static theory and transient dynamics characteristics during the torsion process, as in the case where the size of unloading groove of torque shaft remains unchanged; the effective length stays in the range of 967~267 mm; and the transient time under loading impact is anywhere from 0.005 s to 0.100 s. The result shows a significant difference between the changing process of the shear stress itself and the process of elastic-plastic deformation due to different transient impact time. The shorter effective length of torque shaft means a bigger shear stress. The transient impact time of 0.005 s triggers the average changing rate in shear stress of 5.6 MPa/dm, suggesting that a shorter transient impact time gives a bigger shear stress and consequently a greater change in gradient, producing nonlinearity characteristics; the effective length of 267 mm is associated with the biggest changing rate of shear stress greater than 27 MPa; the shorter length of torque shaft is linked to a positive relationship between the shear stress and the time of impact. The study could provide some reference points for the physical designing of the torque shaft.
shearer; torque shaft; effective length; transient impact time; shear stress
2014-01-16
黑龙江省教育厅科学技术研究项目(12531006)
刘春生(1961-),男,山东省牟平人,教授,研究方向:机械设计和液压传动与控制,E-mail:liu-chunsheng@163.com。
10.3969/j.issn.2095-7262.2014.03.007
TD421.6
2095-7262(2014)03-0251-05
A
