基于改进S变换的直流电动机间接测速研究

雷万忠，许春香

(1.河南工程学院，郑州 451191;2.中州大学，郑州 450044)

0 引 言

直流电动机换向电流的频率信息包含其转速信息［1］。因此，在转动轴不可见或不便安装转速传感器的场合，通过分析直流电动机换向电流频率从而间接求其转速不失为一种行之有效的电机测速方法。

国内一些学者对直流电动机间接测速做了深入的研究。张文海、袁宝国等人从理论上证明了根据直流电动机换向电流间接测速的可行性［1－3］;袁宝国还运用LabVIEW软件间接测量了直流电动机稳态时的转速［4－5］，在技术上实现了直流电动机间接测速;黄进等人运用小波包变换和小波脊线方法获取电机起动时的转矩 －转速特性［6－9］，扩大了根据换向电流求取电机电气信息的范围;崔淑梅采用有限元方法分析了直流电动机的换向电流并提出了新的直流电动机换向电流频率和转速的表达式［10－11］，对直流电动机电刷同时换向时的测速公式做了进一步补充。黄传金等人运用经验模态分解和局部均值分解来提取直流电动机的高频换向电流［12－13］。

就电机间接测速而言，若要测量起动时的特性，目前常用的方法是小波包变换(WT)［6］和小波脊线算法［8－9］。小波包变换分析直流换向电流时，对噪声比较敏感，常采用小波阈值滤除噪声，但如何确定合适的阈值，还需进一步研究，而且由于其通过拟合离散点得到连续的转速曲线，测量精度较低，另外，小波变换无法借助FFT快速实现;小波脊线算法对噪声不敏感，可直接分析电机换向电流，由于其属于连续小波变换(CWT)，测试精度要优于小波包变换的方法，但小波脊线算法的庞大计算量给其在直流电动机间接测速领域的应用带来困难。快速且易于实现的直流电动机间接测速方法是其能否推广应用的关键。

Stockwell等人于1996年提出了一种新的时频分析方法－S变换［14］，其继承和发展了小波变换和短时傅里叶变换的局部化思想，是一种可逆的时频分析方法，并且可用现有的傅里叶算法实现S变换的快速计算。在电力工程信号领域，S变换已成功应用于电能质量信号的检测［15－18］。本文提出了基于改进S变换的直流电动机间接测速新方法，通过调节时频因子分离噪声和直流分量得到换向电流，然后对换向电流进行改进S变换运算，对该变换利用时频分布最大化原则估计瞬时频率［19］，从而实现了直流电动机间接测速。

1 S变换原理及其改进

1.1 S 变换原理［14－15］

S变换的核心思想是对短时傅里叶变换和小波变换的扩展，是一种可逆的时频分析方法，信号x(t)的连续S变换s(τ，f)定义如下:

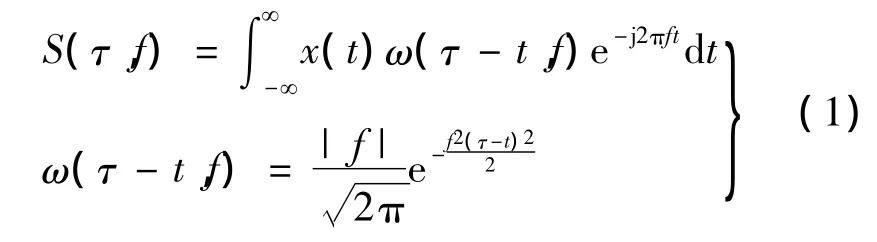
式中:τ为时移因子;f为频率;ω(τ－t，f)为高斯窗函数。

信号x(t)可由S变换重构，其S逆变换:

从式(1)可知，高斯窗函数的宽度和频率呈反方向变换，而幅值和频率是线性关系，克服了短时傅里叶变换窗口高度和宽度固定的缺陷。由式(2)可知，利用S变换及其逆变换可实现信号时域和频域间的相互转换。

设 τ =mTs，f=，则x(nTs)的一维离散S变换:

式(3)中:Ts为采样时间间隔;N为采样点数;k，m，n均在［0，N－1］之间;X(k/NTs)是信号 x(nTs)的离散FFT变换;G(r，k)为高斯窗的FFT频谱，且有:

由此可见，通过快速傅里叶变换可实现对离散信号x(nTs)的S变换，且每个点的运算次数与FFT相同。

1.2 改进S变换

S变换中的高斯窗函数的宽度和高度随频率变化而变化，但其存在白噪声功率谱随频率增高而线性增大和时频分辨率变化趋势不变等问题［17］。直接将其用于直流电动机间接测速，很难将换向电流与噪声成分、直流电流分离。为此，提出基于改进的S变换的直流电动机间接测速方法。改进S变换定义［17］:

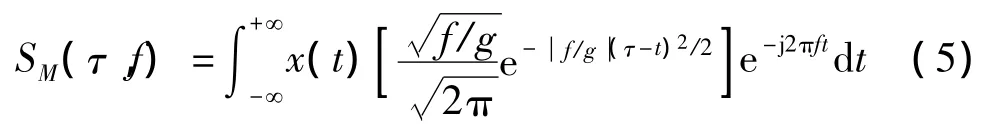
由式(5)可知，改进S变换增加了可调整时频分辨率的参数g，与S变换的不同在于高斯窗函数的窗宽与频率平方根的倒数成正比。根据卷积定理，可得改进S变换的离散表达式:

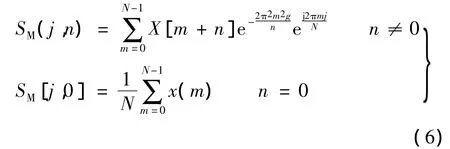
式中:n，j分别是频率采样点和时间采样点;X(n)是信号x(k)的离散傅里叶变换;N是序列信号的总长度。

改进S变换结果为一个二维矩阵，记为S矩阵。S矩阵的列对应频率，行对应采样时刻，矩阵元素为相应频率信号不同时刻的幅值。

由于高斯窗函数满足归一化条件，按j将SM累加，SM可看作是离散傅里叶变换，即:

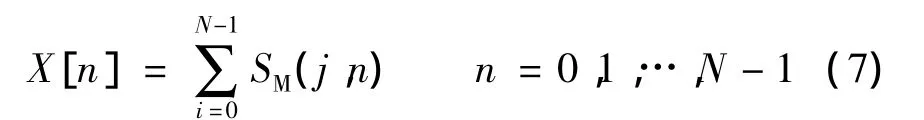
由式(7)的离散傅里叶反变换可得改进S变换的逆变换，即:

由上式可知，根据卷积定理和FFT，可实现改进S变换及其逆变换的快速运算。

2 间接测速公式和试验采集方案设计

2.1 直流电动机间接测速公式

由于直流电动机绕组形式的多样性以及换向片数目、极对数多少的不确定性，还没有一个固定的公式适用于所有类型的直流电动机，但极对数为1的直流电动机的间接测速公式得到广泛认可［1］，其数学表达式［6］:

式中:m为换向片数;n为转速;p为极对数;c由m的奇偶决定的系数，m为偶数时，c=1;m为奇数时，c=2。

2.2 试验采集方案

本文以某微型永磁直流电动机为测试对象，其换向片数目为12、极对数为1。铭牌数据:额定电流IN=1.25 A;额定电压UN=12 V;额定功率PN=15 W;空载电流为0.18 A;空载转速为2000 r/min。

采集系统由闭环霍尔电流传感器LSTR25N、数据采集卡ARTUSB2850、PC机和直流电源组成，如图1所示。其中，LSTR25 N线性度0.1%、次边和原边比为2000、取样电阻为50 Ω、频带宽为DC－100 kHz。ART USB2850数据采集卡完成放大和转换功能，该采集卡中输入转换芯片为16位的AD7665ASTZ，模拟输出转换芯片为 12位的AD5725，测量精度为0.01%，采样速率最高可达500 kHz。PC机的数据处理软件为MATLAB 2011a。

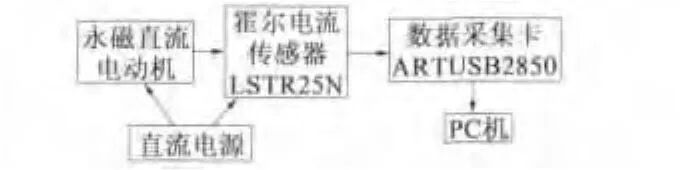
图1 数据采集系统

在整个数据采集系统中，采样频率的选择至关重要，采样频率过高将导致运算量成倍增加，不仅会造成测试系统实时性较差，而且也增加硬件成本，甚至运算量会超出计算机内存处理范围;如采样频率过低，将不能正确获取高频的换向电流。由于直流电动机从起动瞬间到进入稳态时刻，转速不断增加，从而可以判断高频换向电流频率在稳态时最大，本文根据换向电流频率和空载转速间的关系，根据额定的空载转速初步判断稳态时的换向电流频率，然后，根据乃奎斯特采样定理，本文采样频率为10 kHz，采集的直流电动机空载起动时的电流及其傅里叶谱如图2所示。

图2 直流电动机起动电流及其傅里叶谱

由图2(a)可知，直流电动机起动时的电流较大，然后逐渐减小进入稳态，另外，电枢电流还含有噪声;由图2(b)可知，直流电动机电枢电流中的直流分量很大;由图2(b)的局部放大图可知，电枢电流有噪声成分。另外，幅值较大的高频信号主要有两处，一处频率为364 Hz，可认为是进入稳态后的高频换向电流频率;另外一处在150 Hz附近，究其原因主要是刚开始起动时阻碍换向的自感电动势和互感电动势很小，帮助换向的旋转电动势引起的换向电流较大。

3 基于改进S变换的直流电动机间接测速

3.1 换向电流提取

S变换虽有很多优点，但很难将S变换直接用于提取换向电流。主要因为S变换中的基本小波是固定的，其频率分辨率无法调整，而直流电动机空载起动电流中直流成分很大，而噪声信号和换向电流很小，很难将它们从电枢电流中提取出来。图3为空载起动时电枢电流S变换的三维网格图，从图中可知直流成分将换向电流“淹没”，S变换没有分辨出换向电流。

图3 起动电流S变换的三维网格图

改进的S变换增加可调整时频分辨率的参数g，g趋向于0时，只有时间分辨率;g趋向于无穷时，只有频率分辨率［19］。但定量的确定g很困难，在电能质量滤除噪声时，实验发现g=0.024能量集中在较小的区域，利于滤除噪声［17－18］。与滤除噪声不同在于，应用改进S变换进行直流电动机间接测速时不仅要滤除噪声，还要滤除直流分量，进而将换向电流提取出来。图4为g改变时对图2(a)的空载起动电流进行改进S变换得到的空载起动电流的三维网格图。从图4(a)可知，g=0.024时能量集中在很小的区域，换向电流被“淹没”;由图4(b)可知，增加g可提高改进S变换的频率分辨率，但g=240时，与图2(b)的直流电动机空载起动电流的傅里叶谱对比可知，高频换向电流还没有完全被突出;从图4(c)可知，当g=1200时换向电流被很好的分离。大量实验发现，g在780至1200时都可将换向电流与直流分量、噪声分量分离开来，同时，为尽量提高时间分辨率，本文取g=800，其对应的三维网格图如图5(a)所示，改进S变换中幅值最大值行向量如图5(b)所示，幅值最小值行向量如图5(c)所示。从图5(b)、5(c)可知，低频直流成分、高频噪声信号都被很好地分离。将低频的直流成分和高频的噪声信号去掉，并对其进行逆变换，得到的换向电流如图6所示，从中可知电流噪声被很好地滤除，本文所提方法可以很好地提取换向电流。

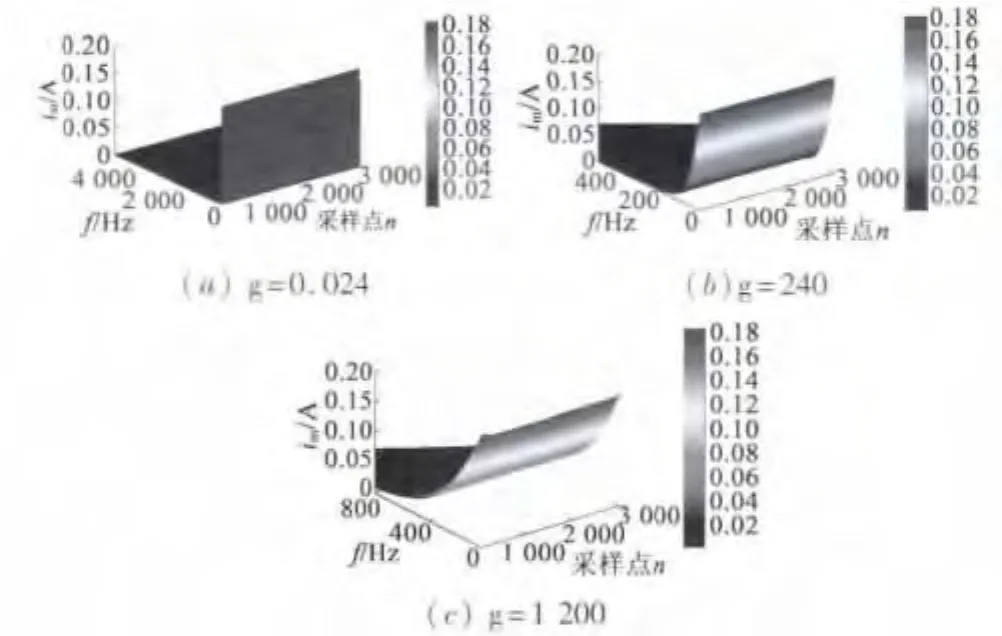
图4 起动电流改进S变换的三维网格图

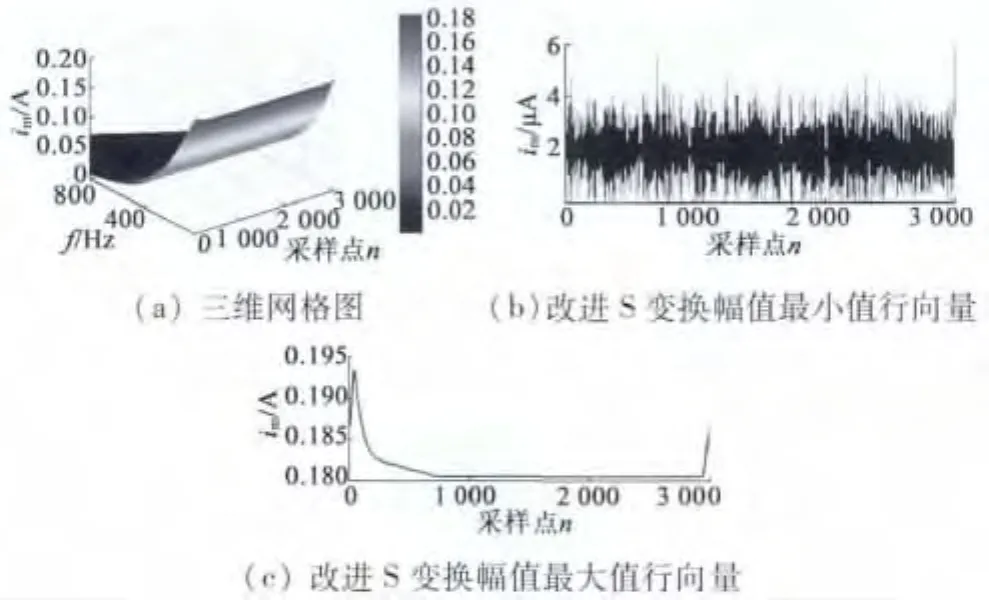
图5 g=800时空载起动电流改进S变换

图6 应用改进S变换提取的换向电流

3.2 换向电流频率

直流电动机起动时的电流可视为渐进的单分量信号，用小波变换进行直流电动机间接测速时可用脊线算法提取其频率信息［8］。用改进S变换进行直流电动机间接测速时可用类似方法，即根据改进S变换的时频分布最大化原则估计瞬时频率(脊线算法)［19］，其本质是找出时面上每一时刻的最大值，并将其对应的频率作为每一时刻估算出的瞬时频率，可用公式表示:

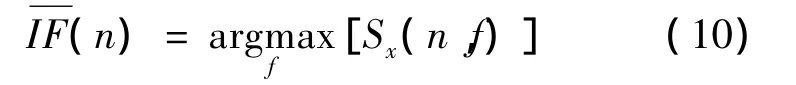
式中:f为采样频率;n为采样点数。

直流电动机换向是复杂的物理、机械和化学过程，很难做到直线换向，常存在提前换向的现象(由图6的局部放大图中可知存在提前换向情况)。由此带来了高频毛刺成分，给直流电动机间接测速带来了困难。为此，本文根据已知的额定空载转速、直流电动机转速和频率间的关系设置一个频率阈值fmax，然后应用式(10)估算出的换向电流频率，如果在某采样点根据式(10)估计的频率大于fmax时，则用上一采样点估计的频率作为该采样点的频率。采用该方法估计的瞬时频率如图7所示，应用式(9)得到的直流电动机空载起动时的转速曲线如图8所示。

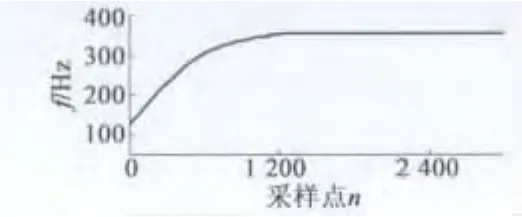
图7 换向电流频率

图8 直流电动机空载起动时的转速曲线

从图8可知，稳态转速为1814 r/min，在实验中用闪光测速仪DM6234P+测得的直流电动机稳态转速为1817 r/min，由此可知，本文所提的直流电动机间接测速方法具有较高的精度。

4 结 语

本文提出了一种基于改进S变换的直流电动机间接测速新方法，该方法吸收了短时傅里叶变换和小波变换的优点，并可通过现有的快速傅里叶变换实现改进S变换的快速运算，实现了直流电动机间接测速的快速计算。本文通过实验方法确定了可调整时频分辨率的参数g，如何定量地确定时频因子还需进一步研究。

［1］袁宝国，曹镇荣，王胜国.直流电动机反电动势对其电流脉动频率的影响［J］.中国电机工程学报，2007，27(30):92 －96.

［2］袁宝国.换向过程对直流电动机电流脉动频率影响的分析［J］.2007，40(5):36 －38，48.

［3］张文海.直流电动机的转速测量方法［J］.微电机，1996，29(4):38－40.

［4］袁宝国.微型直流电动机无传感器测速的虚拟仪器设计［J］.微特电机，2006，34(11):44 －45.

［5］袁宝国，周政新，胡志华.直流电动机无传感器实验方法［J］.微特电机，2007，35(11):20 －22.

［6］黄进，黄建华，张伟，等.基于小波分析的直流电机转矩－转速特性测试［J］.中小型电机，2001，28(2):49－53.

［7］魏云冰，黄进，黄建华.基于小波包变换的电机测试信号去噪处理［J］.电工技术学报，2001，16(5):64 －67.

［8］牛发亮，黄进.渐进信号瞬时频率提取及其在电机性能测试中的应用［J］.电工技术学报，2006，21(4):122 －126.

［9］黄传金，宋海军，陈铁军，等.基于小波脊线的异步电动机间接测试方法［J］.电机控制与应用，2012，39(11):44 －46.

［10］刘曼兰，张千帆，崔淑梅.直流电机转速与电流换向脉动频率关系新表达［J］.微电机，2006，39(5):10 －13.

［11］崔淑梅，陈钊，宋立伟.直流电机换向有限元仿真模型的研究［J］.微电机，2011，44(2):1 －5.

［12］黄传金，宋海军，陈铁军，等.微型直流电动机电枢电流提取新方法［J］.微特电机，2013，41(4):10 －13.

［13］黄传金，宋海军，陈铁军，等.基于EMD滤波的直流电动机启动电流高频分量提取方法［J］.微特电机，2013，41(5):28－31.

［14］STOCKWELL R G，MANSINA L，LOWE R P.Localization of the complex spectrum:the S transform［J］.IEEE Trans.on Signal Process，1996，44:998 －1001.

［15］赵凤展，杨仁刚.基于S变换和时域分析的电能质量扰动识别［J］.电网技术，2006，30(15):90 －94，100.

［16］唐求，滕召胜，高云鹏，等.基于S变换的平方检测法测量电压闪变［J］.中国电机工程学报，2012，32(7):60 －67.

［17］易吉良，彭建春，谭会生.基于改进S变换估计电能质量信号的噪声水平［J］.电网技术，2009，33(20):71 －75.

［18］易吉良，彭建春，罗安.电能质量信号的改进S变换降噪方法［J］.仪器仪表学报，2010，31(1):32 －37.

［19］SHUI P L，SHANG H Y，ZHAO Y B.Instantaneous frequency estimation based on directionally smoothed pseudo－wigner－ville distribution bank ［J］.IET Radar Sonar Navig，2007，1(4):317－325.