单相串励电动机稳态和瞬态性能分析

倪有源，赵 亮，陈 浩

(合肥工业大学，合肥 230009)

0 引 言

随着人们越来越追求高品质的生活，电动工具和家用小电器的需求也大幅度提高。单相串励电机由于调速方便且调速范围较宽，容易实现无级调速，具有较好的恒功率特性，并具有高转速比、起动转矩大、转速高和体积小等特点，被广泛用于吸尘器、搅拌机、吹风机、滚筒洗衣机等家用电器以及电动工具中，更是世界上用量最多的电动机之一［1－2］。因此对单相串励电动机的研究具有重要的工程价值。

国内外学者对单相串励电动机的设计与优化展开了广泛的研究［3－6］，对控制系统也展开了研究［7］。用有限元方法对单相串励电动机的电阻和电感进行了分析［8］。而对于该类电机稳态性能和瞬态性能分析研究却十分匮乏。本文首先利用Ansys RMxprt软件，基于等效磁路法对一台79 W食物搅拌机用单相串励电动机进行了分析，得出了电机稳态性能参数。然后利用Ansys Maxwell 2D软件，采用二维瞬态有限元法优化定子的结构，确定了电机的结构，并得出电机瞬态性能参数和电机起动过程曲线。接着，利用Ansys Maxwell 2D软件精确得出各项铁耗，并与3D计算结果进行比较，二者计算结果接近。最后对电机进行性能测试。电机实测结果与计算结果的一致性验证了计算结果的正确性。

1 单相串励电动机的结构及数学模型

单相串励电动机的模型如图1所示。

图1 单相串励电动机模型

单相串励电动机属于交、直流两用电动机，既可以使用交流电源工作，也可以使用直流电源工作，其等效电路如图2所示。

单相串励电动机的电压方程:

式中:u为端电压;ef和ea分别为激磁绕组和电枢绕组的感应电动势;ra和rf分别为激磁绕组和电枢绕组的电阻;La0和Lf0分别为激磁绕组和电枢绕组的漏感;r1～r6分别为理想接触情况下的电刷与换向片接触电阻;i1～i6分别为通过与电刷接触的换向片电流;es1～es4为短路线圈的感应电动势;r1～r3为电刷与换向器之间的接触电阻;is1～is6是短路线圈电流;rs1～rs3为短路线圈电阻;Ls1～Ls4为线圈端部漏感。

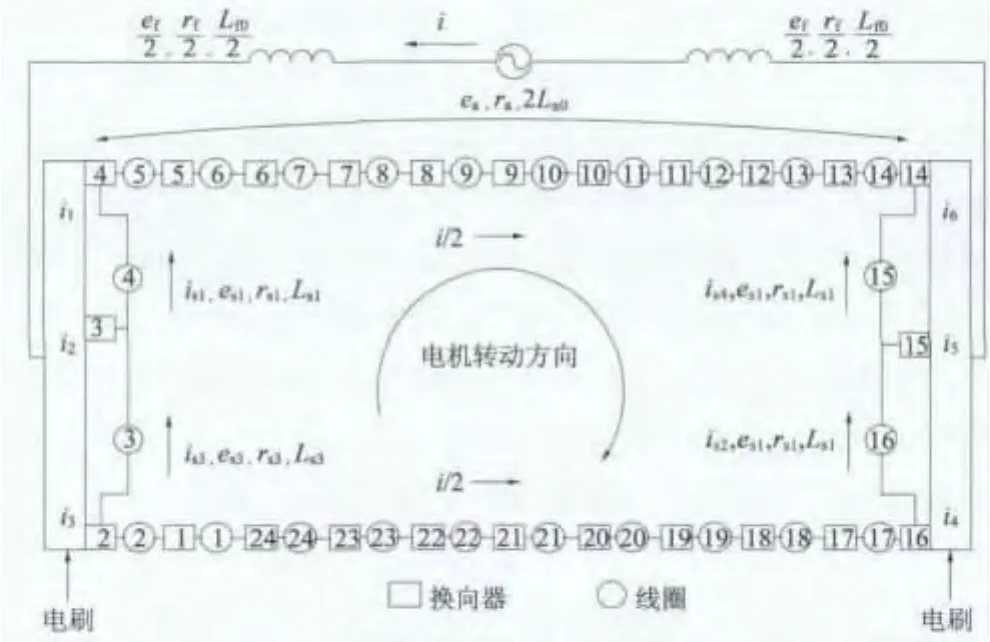
图2 单相串励电动机的等效电路

根据斯托克斯定理，可得:

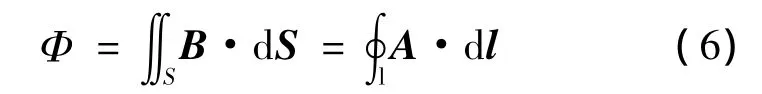
式(1)至式(5)中的感应电动势e可先由磁矢位A对时间t求导，再对闭合路径的线积分获得，即

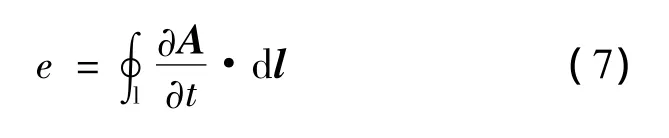
2 等效磁路法计算电机稳态性能

2.1 单相串励电动机的等效磁路

单相串励电动机的等效磁路如图3所示。图中Rs、Rr、Rδ、Rσ分别为定子磁阻、转子磁阻、气隙磁阻和漏磁阻;Φd、Φσ、Φδ分别为励磁磁通、漏磁通和主磁通;Fm和Fa分别为励磁磁动势和电枢磁动势。电枢反应取决于电刷位置和旋转方向。

图3 单相串励电动机的等效磁路

由磁路的欧姆定律可得单相串励电动机的磁路方程:

2.2 单相串励电动机的稳态计算

电机的额定数据如表1所示。

表1 电机的额定数据

单相串励电动机的功率方程:

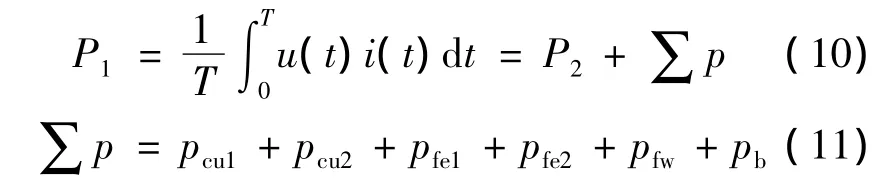
式中:P1为输入功率;P2为输出功率;pcu1和pcu2分别为定子铜耗和转子铜耗;pfe1和pfe2分别为定子铁耗和转子铁耗;pfw为风摩损耗;pb为电刷压降损耗。

表2列出了电机主要结构参数。电机定转子铁心均采用牌号为50W470的硅钢片。

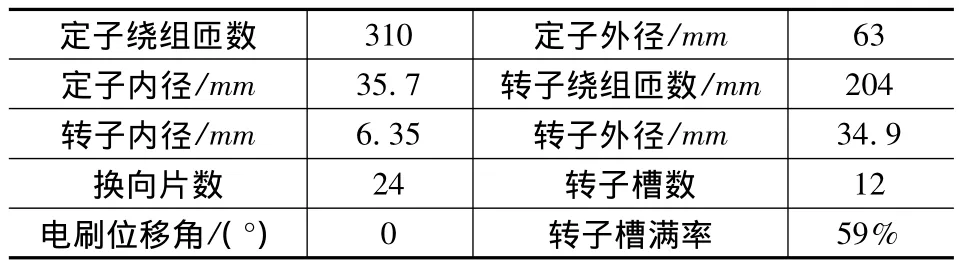
表2 电机主要结构参数

由式(10)和式(11)，用等效磁路法计算可得电机额定负载时的部分稳态性能参数，如表3所示，其他部分参数列于后面的表6中。

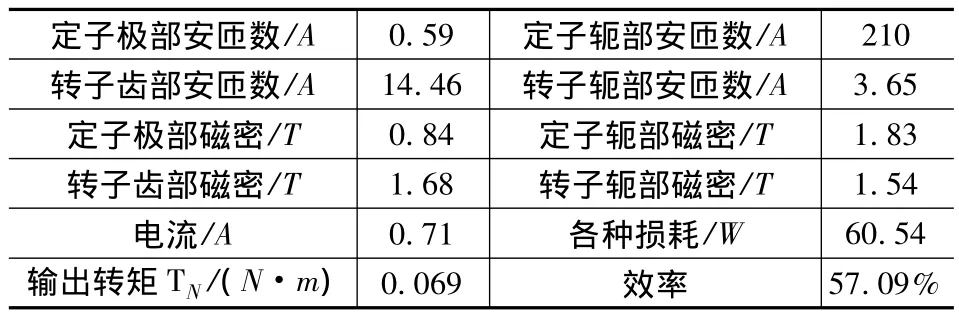
表3 等效磁路法计算得到电机的稳态性能参数

3 有限元法计算电机瞬态性能

3.1 定子结构优化

图4是电机两种不同的定子结构图，图4(b)中定子比图4(a)的多开了2个小槽。

图4 两种不同定子结构图

采用二维瞬态有限元法分析计算，可得电磁转矩的平均值、基波值以及脉动值，如表4所示。

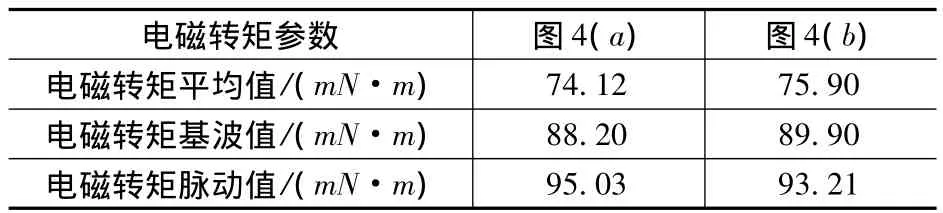
表4 不同定子结构的电磁转矩参数

由表4可以看出，采用图4(b)的定子结构，不仅可增加一定的电磁转矩平均值和基波值，而且可以减小电磁转矩脉动。因此，本文采用图4(b)的定子结构。

3.2 二维有限元法计算磁场及瞬态性能

在二维有限元中，磁矢位A在求解域内满足的矢量泊松方程:

式中:v为磁导率;A为磁矢位;J0为电枢电流的电流密度;Js1～Js4分别为图2中电流is1～is4的线圈短路电流的电流密度。

电机运行在恒定转速下，电机的旋转电角度:

式中:ω为电机的旋转角速度。

采用瞬态有限元法联立求解式(1)至式(5)，可得磁矢位A和电流i。进而可得磁感应强度B=rot A;最后对求解域中每个单元求解偏微分方程，即可获得整个电机磁场分布。

运用有限元软件进行分析，可得电机气隙径向磁密波形，如图5所示。电机定转子铁心的磁密矢量分布如图6所示。

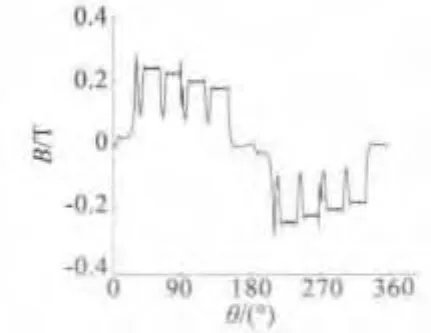
图5 气隙径向磁密波形图

图6 定转子铁心的磁密矢量分布

采用二维瞬态有限元法进行电机计算，可得电磁转矩波形，如图7所示。电机的输入电流波形如图8所示。电机的输入功率波形如图9所示。通过对这些曲线进一步分析，可以得到电磁转矩平均值、输入电流有效值以及输入功率平均值等参数。由式(10)和式(11)。可以进一步获得电机效率等参数。

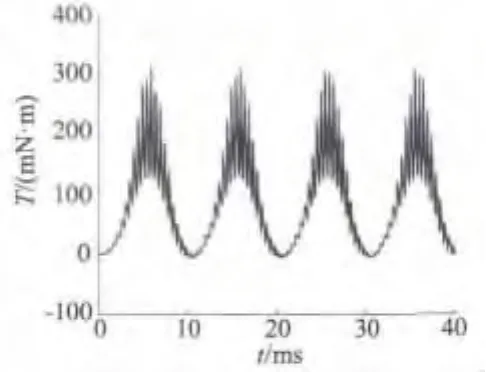
图7 电机的电磁转矩波形

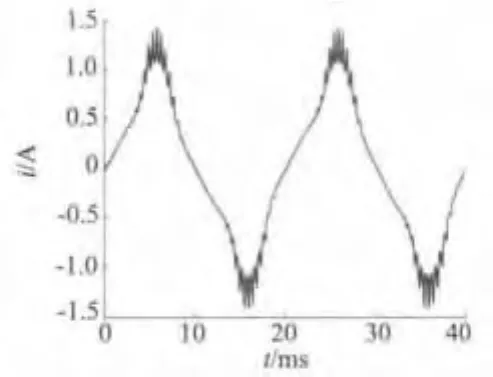
图8 电机的电流波形

图9 电机的输入功率波形

3.3 二维有限元法分析起动过程

考虑到起动过程，单相串励电动机的机械运动方程:

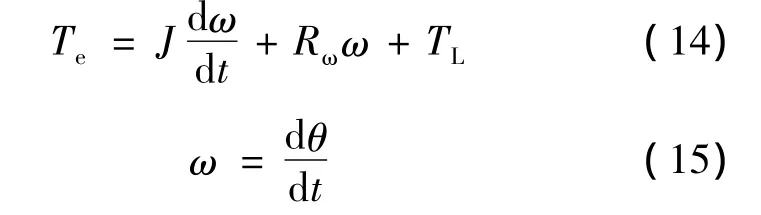
式中:J为转动惯量;Rω为阻尼系数;TL为负载转矩。电磁转矩方程:

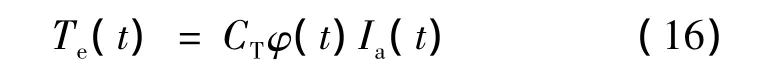
式中:CT为电机的转矩常数;φ(t)为每极磁通;Ia(t)为电枢电流。起动过程的阻尼系数:

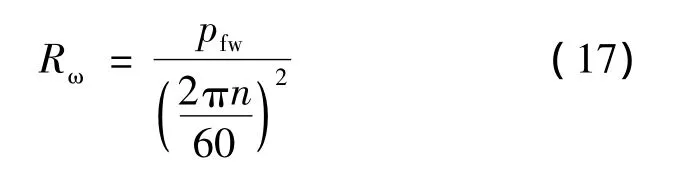
式中:n为转速。

由式(14)和式(15)，利用二维有限元方法，计算可得到电机的起动过程，如图10所示。

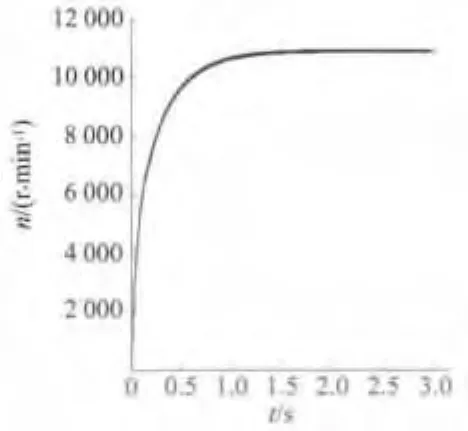
图10 电机的起动过程

3.4 二维有限元法分析各项铁耗

单相串励电动机的损耗包括定子铁心和转子铁心的损耗［9］、激磁绕组和电枢绕组的铜耗、换向器损耗、电刷压降损耗以及风摩损耗等。其中铜耗可计算得出。而精确获得定子铁心和转子铁心的损耗至关重要。利用有限元法求解磁场，结合实际模型可以得到径向磁场和切向磁场的各次谐波幅值［10］。铁心各项损耗可由式(18)获得，风摩损耗可由经验值获得。

式中:Kh为磁滞损耗系数;Kc为涡流损耗系数;Ke为附加损耗系数;Bmax为磁密最大值;f为输入电流的频率。

由式(18)，采用二维瞬态有限元法计算获得的各项铁耗参数如表5所示。

为了验证2D有限元法计算得到的各项铁耗值的准确性，可采用3D有限元法计算。

3.5 三维有限元法计算各项铁耗

在三维有限元中，磁场的基本方程［11］:

采用三维瞬态有限元法，计算得到电机的定转子铁心损耗分布分别如图11和图12所示。

图11 定子铁耗分布图

图12 转子铁耗分布图

从表5中可以看出，二维有限元法与三维有限元法计算的各项铁耗基本一致。

表5 2D FEM和3D FEM得到电机各项铁耗

4 电机的测试结果

图13为电机定转子实物照片。

目前，单相串励电动机性能测试主要使用各种力矩测试系统，可在电机输出端直接耦合标定的加载转矩，从而测出电机的性能［12］。图14为该电机的测试系统。在额定负载下，测试结果与几种方法计算结果分别列于表6中。可以看出，实测结果与计算结果具有较好的一致性。

图13 电机定转子实物

图14 电机测试系统

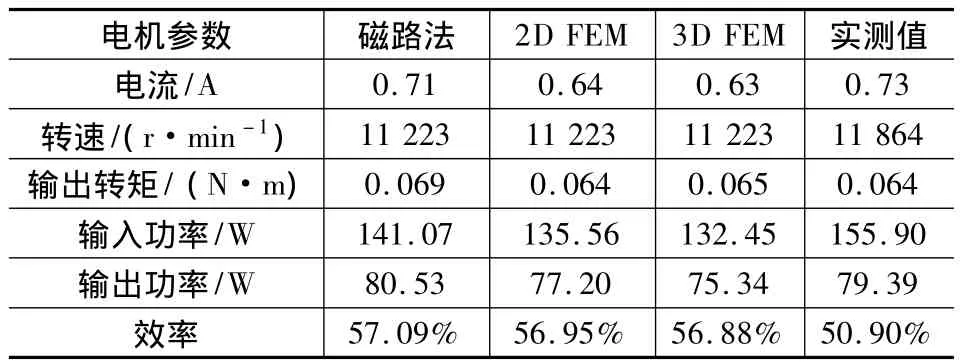
表6 电机额定负载时计算值与实测值

5 结 语

本文分别采用等效磁路法和瞬态有限元法分析与研究了一台食物搅拌机用单相串励电动机稳态性能和瞬态性能。首先采用等效磁路法对电机进行分析，得出了电机稳态性能参数。接着采用二维瞬态有限元法优化定子结构，得出电机瞬态性能参数和电机起动过程曲线。然后对铁耗进行分解，用二维瞬态有限元法计算精确获得各项铁耗，并与三维瞬态有限元法计算结果进行比较。最后，电机实测结果与计算结果的一致性验证了计算结果的正确性。本文对于单相串励电机的性能分析与优化设计具有一定的理论参考价值。

［1］汪镇国.单相串激电动机的原理设计制造［M］.上海:上海科学技术文献出版社，1991:1－2.

［2］金娟.用于滚筒洗衣机的串激电机调速控制技术的研究［D］.南京:南京理工大学，2012.

［3］LIN D，ZHOU P，STANTON S.An analytical model and parameter computation for universal motors［C］//IEEE International Electric Machines＆ Drives Conference(IEMDC)，2011:119－124.

［4］POLAT A，ERGENE L T，FIRAT A.Dynamic modeling of the universal motor used in washer［C］//The Electrical Machines and Power Electronics and Electromotion Joint Conference(ACEMP)，Istanbul，2011:444 －448.

［5］张晶.单相串激电动机多目标优化设计［D］.广东:广东工业大学，2007.

［6］KURIHARA K，SAKAMOTO S.Steady － state and transient performance analysis for universal motors with appropriate turns ratio of lead coils to lag coils［J］.IEEE Transactions on Magnetics，2008，44(6):1506 －1509.

［7］彭华仁.基于模糊PID的串激电机速度控制及参数可视化调试［D］.南京:南京理工大学，2012.

［8］LANDO A D，PERINI R.Modeling of universal motor performance and brush commutation using finite element computed inductance and resistance［J］.IEEE Transactions on Matrices Energy Conversion，2000，15(3):257 －263.

［9］PAPA G.Universal motor efficiency improvement using evolutionary optimization［J］.IEEE Transactions on industrial Electronics，2003，50(3):602 －611.

［10］汤平华，漆亚梅，黄国辉，等.定子无铁心飞轮电机绕组涡流损耗分析［J］.电工技术学报，2010，25(3):27 －32.

［11］KAWASE Y.3 － D eddy current analysis in a silicon steel sheet of an interior permanent magnet motor［J］.IEEE Transactions on Magnetics，2003，39(3):1448 －1451.

［12］史敬灼，王岚，徐殿国.单相交流串励电机无耦合自动测试［J］.电工技术学报，2006，21(11):76－81.