干涉Cartwheel获取高精度DEM的联合校准技术

李 品

(南京电子技术研究所， 南京210039)

0 引言

卫星编队是指若干颗卫星在围绕地球运动的同时，保持彼此之间特定的相对位置关系，共同合作完成某些特定的空间任务。干涉Cartwheel［1］为分布式小卫星编队的一个重要应用，它能充分利用编队卫星构成的空间基线进行干涉测量，合作实现星载合成孔径雷达(Synthetic Aperture Radar，SAR)的干涉测高［2］、测速［3］、高分辨［4］等多项功能。

利用干涉Cartwheel获取地形数字高程地图(Digital Elevation Map，DEM)，用于干涉测量的卫星平台系统参数是影响高程精度的主要原因。为提高DEM精度，可以采用传统InSAR干涉定标方法［5-7］，但这些方法均是基于单根基线的干涉平台。干涉Cartwheel各卫星之间可构成多基线干涉平台，且每根基线均可在满足干涉测高条件下［8］获取地形DEM。因此，利用传统方法对各干涉平台一一定标不但增加了复杂度，而且没有利用编队卫星间相对稳定的位置特性。星间相对稳定的位置信息一般都是通过精确星间测角、测距获得的，但高精度的星间测距或测角对编队卫星的成本要求非常高，且精度不高。因此，如何避免高精度的星间测量，而直接利用编队卫星的空间结构信息的研究显得非常必要。

本文利用干涉Cartwheel的编队构形，建立了编队构形误差和各干涉平台参数误差的关系;并以干涉测高误差的线性化模型为基础，联合各干涉平台的敏感度方程，共同合作完成地形高精度DEM的联合校准。该校准算法从传统定标算法的敏感度方程出发，不需要高精度的星间测量技术来确定各干涉平台的空间结构，将编队构形误差与系统参数误差同时代入联合敏感度方程，对各干涉平台进行地形联合校准。仿真表明，干涉Cartwheel测高模型能利用该算法得到较精确的地形DEM。

1 干涉Cartwheel测高模型

干涉Cartwheel［1］是卫星编队的一种重要构形，其稳定的编队构形能实现星间的基线干涉测量。编队中的各颗卫星具有相同的离心率和半长轴，运动在同一轨道平面内，相对运动轨道为短轴(垂直运动方向)是长轴(沿运动方向)一半的椭圆，如图1所示。现有标准构型的编队卫星个数N=3，均匀分布在轨道上(相差120°)，为不失一般性，本文讨论中取N≥3。

图1 Catwheel轨道空间构形

图1中的卫星S0与Si(i=1，2)能形成干涉基线，当该基线满足干涉测高条件［7］时，就可对地面进行数字高程重建。图2给出了干涉基线的测高几何模型，其中x轴为平台的运动方向，y轴垂直于平台运动轨道，z轴为地心与运动平台连线的延长方向，θ、Β和H分别为卫星S0的天线俯角、侧视角和对地高程，B为S0与Si形成的基线长度，θc为基线与x-y平面的夹角。在MOD方法的视向量分解坐标系［9］下，可得测绘带内任意一点P的高程重建表达式为

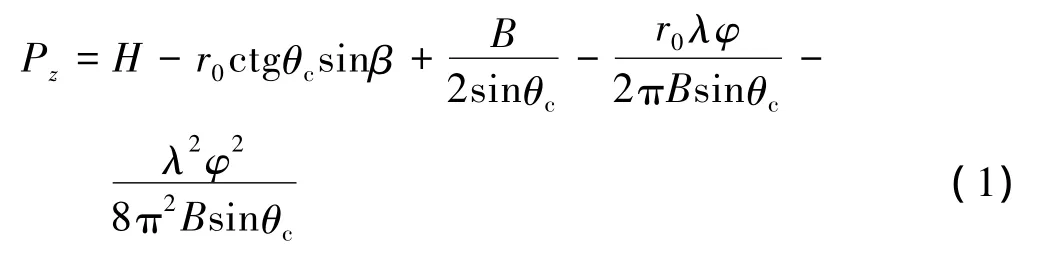
由上式可得:干涉Cartwheel与传统InSAR的测高模型均依赖于系统参数(φ，B，θc，r0，H)，因此必须通过系统参数的定标，以获取高精度的地形DEM。

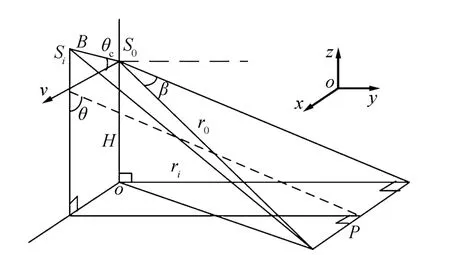
图2 干涉Catwheel测高几何模型

2 测高误差分析

2.1 高程误差的线性化模型

由式(1)可得干涉高程为系统参数的非线性函数。设干涉Cartwheel的编队卫星个数为N，在与其中某一参考卫星S0形成的干涉平台中，满足测高要求的有Ns个(Ns≤N–1)，记S0和Si构成的干涉平台为S0Si平台，其平台系统参数向量为 Xi=〔φ，θc，r0，H，，若为Xi的估计值，则测绘带内任意一点P点的高程估计误差为

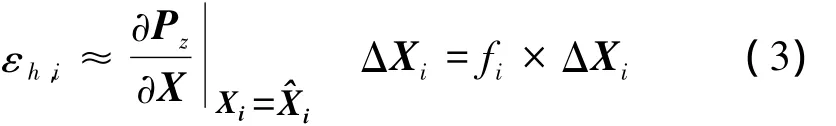
同一干涉平台下，测绘带内各点重建对应的参数误差一致［4］，若在测绘带内放置 L个地面控制点［5］，且已知各点的高程为 Pz，l，l=1，2，…，L。由式(3)得系统参数误差的线性化模型为

式中:ΔHi=［εh，i，1，εh，i，2，…，εh，i，L］T，εh，i，l为 S0Si平台下第 l个地面控制点的重建高程误差;Fi=［fi，1，fi，2，…，fi，L］T为 S0Si平台的敏感度矩阵。

2.2 编队构形误差和系统参数误差的关系

干涉Cartwheel的编队构形中，不同的干涉平台具有不同的系统参数，但各干涉平台的系统参数由编队构形的约束而相互关联。设编队中的两颗卫星(Si和Sj)同时与卫星S0形成测高干涉平台S0Si和S0Sj，则两个平台下的r0和H均基于卫星S0，参数是相同的，误差也相等;此时的其他系统参数均与编队构形有关，但受摄动和空间环境的影响，获得的星间相对构形精度较低，引入构形误差，因此需要进一步的分析构形误差与各参数误差之间的关系。

2.2.1 基线倾角误差与编队构形误差的关系

图3为干涉平台S0Si和S0Sj在轨道平面的几何关系图，由编队构形可得两干涉平台的基线倾角关系为θi，j=θc，j-θc，i，且该基线夹角可由构形的距离信息获取

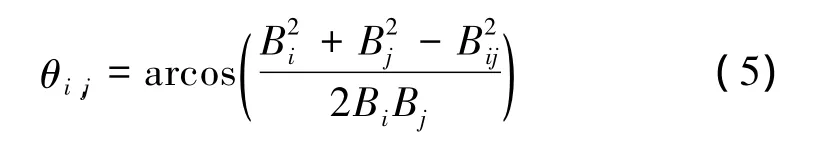
由于构形误差的影响，设由式(5)求得的基线夹角为 θi，j，c，则引入角度误差 δθi，j=θi，j，c– θi，j。设干涉平台S0Sk的基线角度估计值为 θcck，真实值为 θc，k，基线倾角误差 δθcek=θcck– θc，k，k=i，j。则比较 δθcej与 δθcei可得

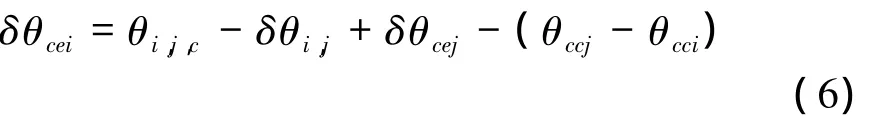
由以上分析，编队构形引入的角度误差 δθi，j越小，则两干涉平台的倾角误差关系越精确。

2.2.2 干涉相位误差与编队构形误差的关系

图2所示的干涉平台S0Si中Si到目标点P的斜距ri可由几何关系表示为

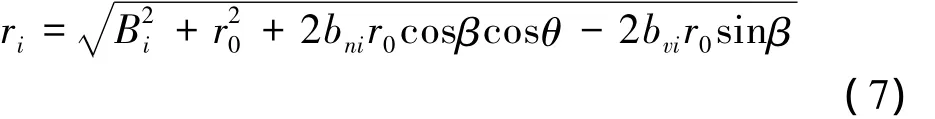
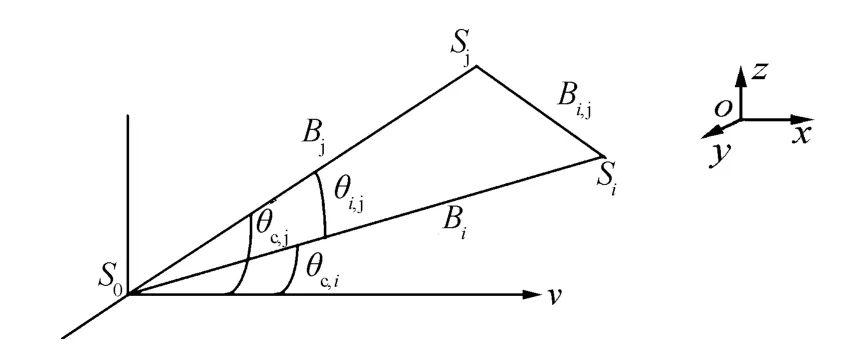
图3 基线角空间几何模型

则该平台下 点的干涉相位 同2.2.1节分析，对于测高干涉平台S0Si和S0Sj，分别得到φi与φj，联立消去S0的俯角θ，可得φi与φj的关系为

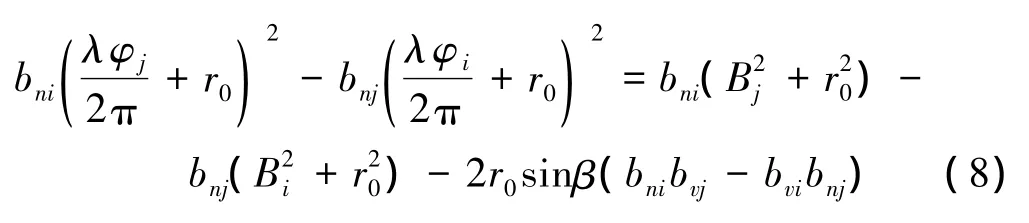
式中:bnk为Bk在z轴的分量，bvk为Bk在x轴上的分量，k=i，j。在干涉测量中，同一距离向上所有目标点的侧视角相同，且斜距r0大大的大于基线长度Bi，则

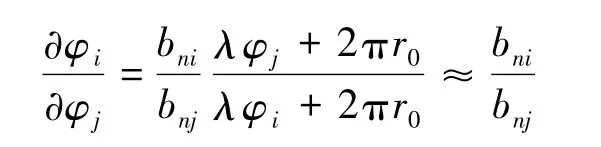
近似为常数。在同一距离向上，式(8)可表示为

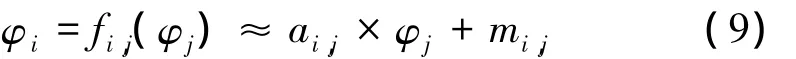
式中:ai，j=bni/bnj;mi，j是 β 的函数。以上关系建立在精确的星间编队构形下，当引入构形误差时，斜率误差为 δai，j=ai，j，c– ai，j。设干涉平台 S0Sk的估计相位为φck，真实值为 φk，干涉相位误差 δφk=φck– φk，k=i，j。比较 φi与 φj得

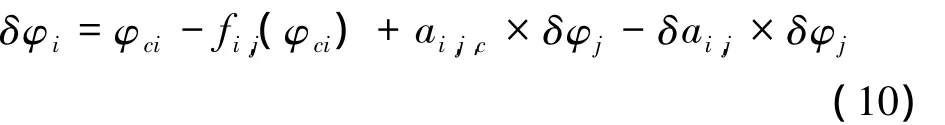
其中，函数 fi，j(·)和斜率 ai，j均和编队构形有关，式(10)即为编队构形误差和干涉相位误差之间的关系。

3 干涉Cartwheel测高的联合校准与误差耦合

3.1 联合校准的敏感度模型

2.2 节给出了各干涉平台的参数误差和编队构形误差的关系表达式，将它们引入线性化测高误差模型。对于测绘带内第l个地面控制点，由式(3)可得平台S0Si和某参考干涉平台S0Sn(i≠n)的参数误差转换，得

其中

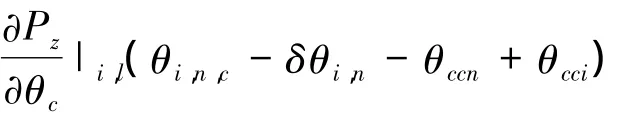
平台S0Si下，对式(4)中的误差线性化模型，令

得

其中，δHi=［δhi，1，δhi，2，…，δhi，L］T;Gi=［gi，1，gi，2，…，gi，L］T。令 δHn=ΔHn，Gn=Fn，将 Ns个干涉平台联立可得

式中:GM为联合敏感度矩阵。式(13)即为多平台的联合敏感度方程，建立了高程重建误差与系统参数误差之间的关系。

3.2 误差的耦合分析

由式(13)可得，联合敏感度方程中的HM与系统参数误差和编队构形误差有关，因此，对于平台S0Si到参考平台S0Sn(i≠n)的参数误差转换中，误差可划分为

其中

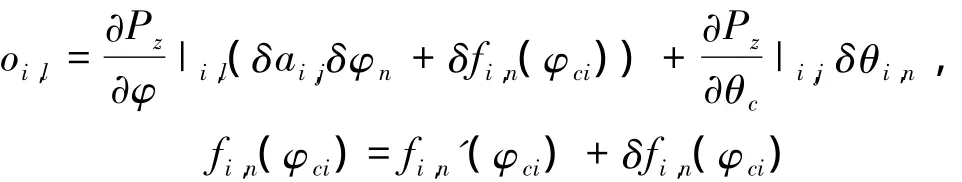
由于编队构形的误差未知，因此利用式(13)获取系统参数误差时，oi，l未知。若令其为0，则该部分构形误差将由ΔSn补偿，具体关系如下

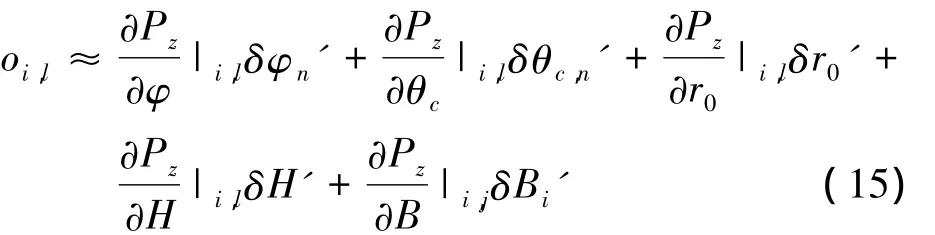
在最小二乘的迭代解法中，可以通过迭代修正系统参数误差。在反复的迭代过程中，系统参数的修正可通过式(6)和式(10)不断修正平台间的参数关系，因此oi，l可以在不断的迭代中通过系统关系修正其带来的影响，使oi，l趋近于0，并最终获得修正后的地形DEM。

3.3 地形DEM校准方案

Cartwheel各干涉平台一共构成Ns×L个定标方程，因此，在引入编队构形的冗余信息后，可以采用适当的参数估计方法对其进行估计，从而进行高程地形校准，具体流程如图4所示。

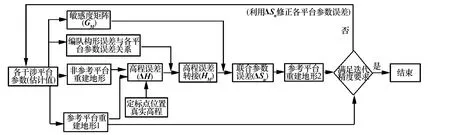
图4 地形校准流程图

以上算法流程中由于编队构形误差与系统参数误差的互相耦合，使系统参数的校准值不可靠，但算法收敛的目标函数是各定标点的真实高程，因此，可重建出精确的地形DEM。

4 算法仿真

选取干涉Cartwheel编队卫星个数N=3，均匀分布在互绕轨道上，且互绕椭圆的短轴为4 000 m，选取某一时刻有效干涉测高平台数Ns=2，各干涉平台参数如下表。

表1 Cartwheel编队卫星的系统参数

以下对于1 km×1 km的平地地形(图5)和复杂地形(图6)分别用本文的校准方法对进行地形高程重建，取地面控制点个数L=4，在测绘带内沿正恻视距离向布放［5］，坐标为(500，200)、(500，300)、(500，500)和(500，700)。引入系统参数误差:基线长度误差 δB1=0.2 m，δB2=0.1 m，相位误差 δφ1=6°，δφ2=8°，倾角误差 δθc1=0.003 5°，δθc2=0.002 8°，斜距误差δr0=5 m，平台高度误差 δH=-3 m。

图5 参考平地地形

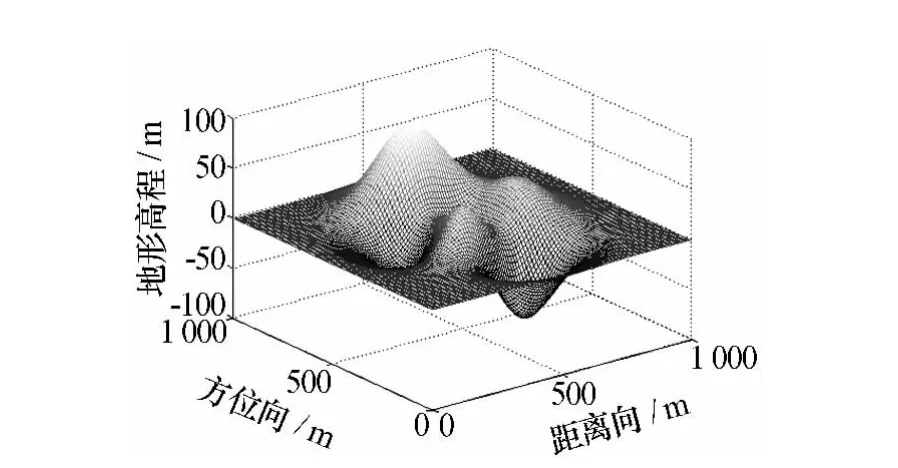
图6 参考复杂地形

引入本文地形校准算法后，不同参考地形下不同参考平台的高程误差，如图7～图10所示。比较各图可见:对于同一参考地形，平台(B1)的重建高程精度较高，这是由于算法是以该平台为参考进行迭代收敛的，因此精度更高;对于同一干涉测高平台，复杂参考地形比平地参考地形的重建高程精度更高，这是因为高度的起伏加大了各参数敏感度的变化，因此联合校准算法中的敏感度矩阵病态性得到一定改善，结果精度更高。

图7 平台(B1)平地地形校准后的高程误差

图8 平台(B2)平地地形校准后的高程误差

图9 平台(B1)复杂地形校准后的高程误差

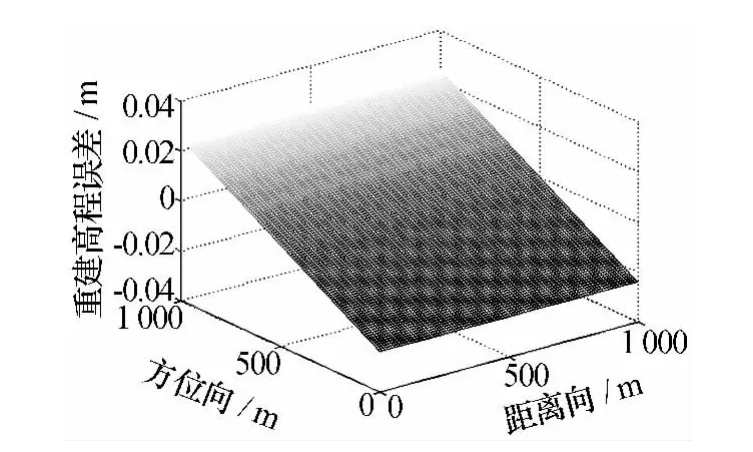
图10 平台(B2)复杂地形校准后高程误差

5 结束语

本文建立了干涉Cartwheel中各干涉平台参数误差和编队构形误差的关系，并将其引入联合敏感度方程，在不需要星间精确测量的基础上利用编队几何构形，实现多平台地形联合校准。它实现了空间位置信息和系统参数之间的自适应，得到较好的校准地形，但由于误差间的耦合，算法未能获取精确的系统参数信息，该问题的研究将在进一步的工作中展开。

［1］Massonnet D.Capabilities and limitations of the interferometric cartwheel［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39(3):506-520.

［2］杨 磊，赵拥军，王志刚.基于估算垂直基线获得高程数据的方法［J］.现代雷达，2006，28(1):52-54.Yang Lei，Zhao Yongjun，Wang Zhigang.Vertical baseline estimation-based method for obtaining digital elevation information［J］.Modern Radar，2006，28(1):52-54.

［3］Goldstein R M，Zebker H A.Interferometric radar measurements of ocean surface currents［J］.Nature，1987(328):707-709.

［4］Prati C，Rocca F.Improving slant-range resolution with multiple SAR surveys［J］.IEEE Transactions on Aerospace and Electronic Systems，1993，29(1):135-143.

［5］Mallorqui J J，Bara M，Broquetas A.Calibration requirements for airborn SAR interferometry［C］//SAR Image A-nalysis，Modeling，and Techniques III.［S.l.］:SPIE Press，2000:267-278.

［6］Dall J.Corss-calibration of interferometric SAR data［J］.IEE Proceedings Radar Sonar Navigaction，2003，150(3):177-183.

［7］郑 芳，马德宝，裴怀宁.InSAR中基线精度要求的探讨［J］.现代雷达，2005，27(9):18-21.Zheng Fang，Ma Debao，Pei Huaining.Discussion about requirement of baseline precision in InSAR［J］.Modern Radar，2005，27(9):18-21.

［8］Krieger G，Fiedler H，Mittermayer J，et al.Analysis of multistatic configurations for spaceborne SAR interferometry［J］.IEE Proceedings Radar Sonar and Navigation，2003，150(3):87-96.

［9］Madsen S，Zebker H，Martin J.Topographic mapping using radar interferometry［J］.IEEE Transactions on Geoscience and Remote Sensing，1993，31(1):246-256.