一种高分辨率多基线InSAR三维层析成像方法

柳祥乐，何向成，杨汝良

(1.湖北汽车工业学院电子信息系， 湖北十堰442002)(2.中国航天二院第二十五研究所， 北京100854;3.中国科学院电子学研究所， 北京100190)

0 引言

合成孔径雷达(SAR)通过采用距离向脉冲压缩、方位向合成孔径技术来实现高分辨率的地形成像。SAR所成的像是二维像，是三维分布的散射体在二维平面上的一个投影。干涉合成孔径雷达(InSAR)有两副天线，一副天线发射雷达波，两副天线同时接收回波，两副天线接收的回波具有一定的相干性，经干涉处理后便可得到能反应地形高度的三维成像［1］。然而，InSAR所成的三维像只是地表的高度像，是一个面图，并不是反映散射体空间分布的立体三维像。由于只有两副天线，InSAR对高度向上分布的散射体分辨力很差，难以实现真正的立体三维成像。

有两种方案可以获得高度向的分辨能力，一种是利用多通道的极化信息，这就是极化干涉测量(PoIn-SAR)，另一种称为多基线 InSAR(Multi-baseline In-SAR)，又称为“多基线层析成像SAR”(Multi-baseline Tomography SAR)。

多基线InSAR是传统InSAR的扩展，传统的In-SAR系统只有一条基线，而多基线InSAR在垂直于视线的方向依次增加多副SAR天线，或用重复航过的方式对同一地区成像，相当于在垂直于视线的方向上合成了一个较大的孔径，因而可以获得高度向上的分辨力。当用波长较长的电磁波对诸如冰、土壤、森林植被等半透明的媒质进行照射成像时，利用其高度向的分辨力，能够得到任何一个断层的影像，这一点类似于CT和核磁共振(NMR)的断层摄影技术，因此，多基线InSAR此时也被称为层析成像SAR(Tomography SAR)。多基线InSAR的示意图可用图1来所示，图中共有K条航线或K副天线，它们沿着垂直于视线方向的圆弧排成一列。

图1 多基线InSAR示意图

早期的多基线InSAR研究多在实验室进行，一般是三天线系统，虽然基线的数量很少，但在植被研究、干涉和层析成像方面也获得了一定的应用［2-3］。德国宇航局(DLR)首次成功地使用其机载E-SAR系统进行了层析成像飞行实验［4］，对Oberpfaffenhofen地区进行了真正意义上的层析成像，他们采用的是载机重复航过的方式，得到14个平行的航线(13条基线)，实现了高度维的聚焦成像。在星载情况下，用小卫星编队飞行的“分布式SAR”也能够形成层析成像所需要的构形。虽然提出的时间不长，但多基线层析成像在地质学、林学、考古学及冰川研究中都展示出了巨大的潜力。

多基线InSAR三维成像处理的一般步骤是:先对观测区进行常规的二维SAR成像，得到同一区域的多幅高分辨率图像，然后对多幅图像进行精确配准，最后对配准后的多幅图像进行高度维成像聚焦。二维SAR成像技术目前已经比较成熟，多基线InSAR三维层析成像最主要的难点是高度维的成像问题，目前主要高度维成像算法是采用DFT聚焦技术，由于实际多基线InSAR系统中基线的数量(对应于飞行航线数)比较少，在满足空间采样定理的条件下，使高度维的合成孔径长度较短，受限于瑞利界，高度维的分辨率较低，而靠增多基线条数来提高分辨率对多基线InSAR系统来说又非常不现实。为提高高度维的成像分辨率，本文将阵列信号处理技术引入到多基线InSAR高度维成像中来。仿真实验表明，这种成像方法可以突破瑞利界的限制，在保持基线条数较少的情况下大大提高高度维的分辨率，实现超分辨成像。

1 多基线InSAR三维层析成像之高度维成像的阵列信号模型

如上所述，基于DFT算法的多基线InSAR三维成像的基本过程是:首先，对各个天线所得的数据进行常规的SAR成像处理，得到多幅二维SAR复图像，对这些复图像使用一定的方法进行高精度的配准，使各个同名点对齐;然后，对配准后的复图像沿高度维逐点进行傅里叶变换，将数据变换到空频域即可得到高度维上的影像［4］。三维成像处理的步骤如图2所示。

多基线InSAR的方位向和距离向的成像与常规的二维SAR成像没有区别，其特殊之处在于高度维聚焦成像。如前所述，通常受限于实际条件，多基线In-SAR的基线条数非常少，而基线长度受到空间奈奎斯特采样定理约束，不能太长，于是在高度维总的合成孔径长度受限，高度维分辨率较低。从实际情况看，基线条数通常少于20，采样数据序列的长度很短，而与之相比，距离向和方位聚焦成像时，满足采样定理约束的数据点常常能达到数千个。在有限的数据集下获得更高的分辨率，可以使用阵列信号处理技术，为此首先需要建立一个基于阵列信号处理的多基线InSAR高度维成像模型。为集中研究高度维的聚焦问题，本文假定SAR系统的二维点扩展函数是理想的δ函数(实际上是sinc函数)，在方位向、距离向已经实现了理想的聚焦。

图2 多基线InSAR三维成像处理原理框图

图1中，r表示斜距向，即视线方向，n表示垂直于视线的方向。通常各个SAR天线都沿着垂直于视线方向的一个圆弧上排列，但由于各条天线之间的间距都远小于它们到成像目标区的距离，因此可以近似地认为K副天线都排列在一条直线上，形成一个天线阵，如图3所示。

图3 简化的多基线InSAR成像几何(距离/高度维截面)

当天线尺寸和基线长度远远小于天线相位中心到成像区域的距离时，多基线InSAR的阵列信号模型可以表达为

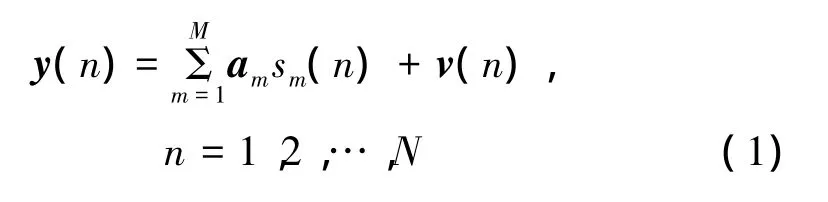
这是一个多视模型，变量n表示第n视，共有N视。M是距离/方位平面上某点对应的高度线上的散射点的个数，本文中假定散射点的个数是已知的。对确定的n，y(n)和v(n)都是K维的复矢量，y(n)表示接收数据矢量，v(n)表示加性噪声。sm(n)是高度向上第m个散射点的复反射系数，可以认为它是一个窄带信源。am是第m个源的方向矢量，在均匀阵列的情况下

式中:上标T表示转置;φm是对应于全长基线(即在阵列中最外侧的两个天线间的基线长度)的干涉相位，根据InSAR的模型，它可以表示为

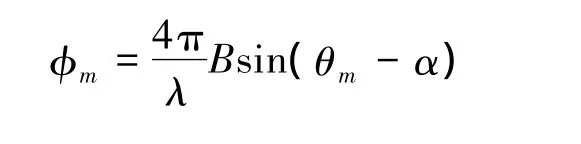
式中:θm是参考天线(如第1个)对第 m个源的入射角;α是天线倾角;B是全基线长度;λ是雷达波长。

am也可以表示成另外一种形式，设以第1个天线为参考天线，对第m个目标第2个天线与第1个天线间的干涉相位为

式中:d是各个天线间的间距，即基本基线的长度。在均匀阵列的情况下，各个基线对应的干涉相位为

φmk=(k-1)ωm，(k=2，3，…，K)

于是方向矢量

am=〔1，ejωm，ej2ωm，…，ej(K-1)ωm〕T

于是模型(1)可以表示成简洁的矩阵形式

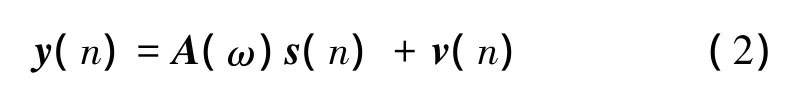
式中:y(n)=［y1(n)，y2(n)，…，yK(n)］T(n=1，2，…，N)是一个 K×N的接收数据矩阵;s(n)=［s1(n)，s2(n)，…，sM(n)］T(n=1，2，…，N)是 K×N 的信源矩阵;v(n)=［v1(n)，v2(n)，…，vk(n)］T(n=1，2，…，N)是 K×N的噪声矩阵;A(ω)是方向矩阵

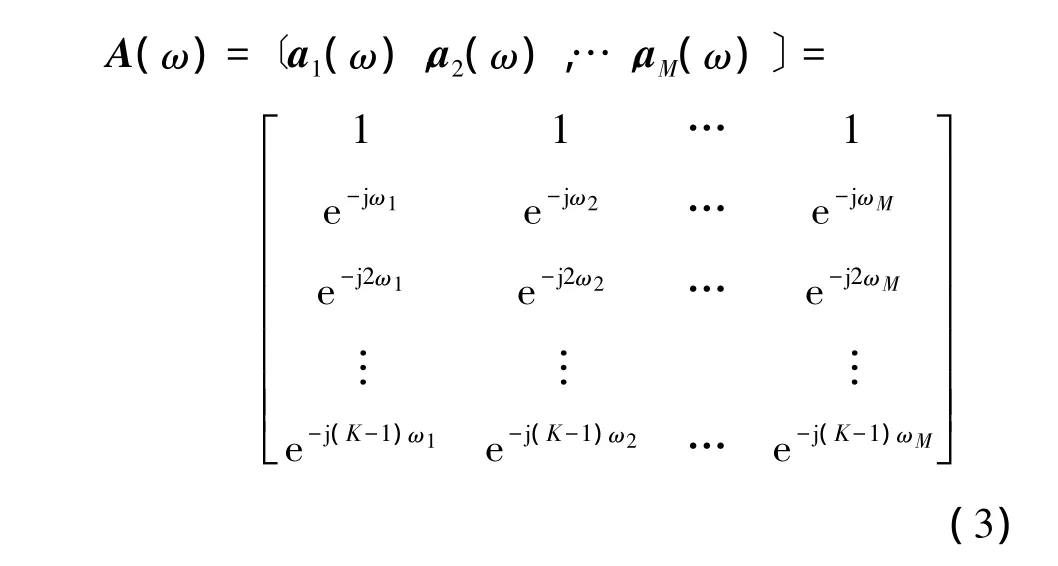
当阵列均匀时它是一个Vandermonde矩阵。

上面提到的变量n表示的是第n视，共有N个视数据，这里的视数是指“N个单视”图像数据，相当于阵列信号处理中的快拍数。多基线InSAR超分辨率高度维成像模型要求在常规的SAR二维成像过程中存储N幅单视复图像。这可以在距离向压缩完成后，方位向处理之前加上预置滤波器，然后再进行各个单视的成像处理，同时存储多个单视复图像，一种典型的处理方法如图4所示［5］。

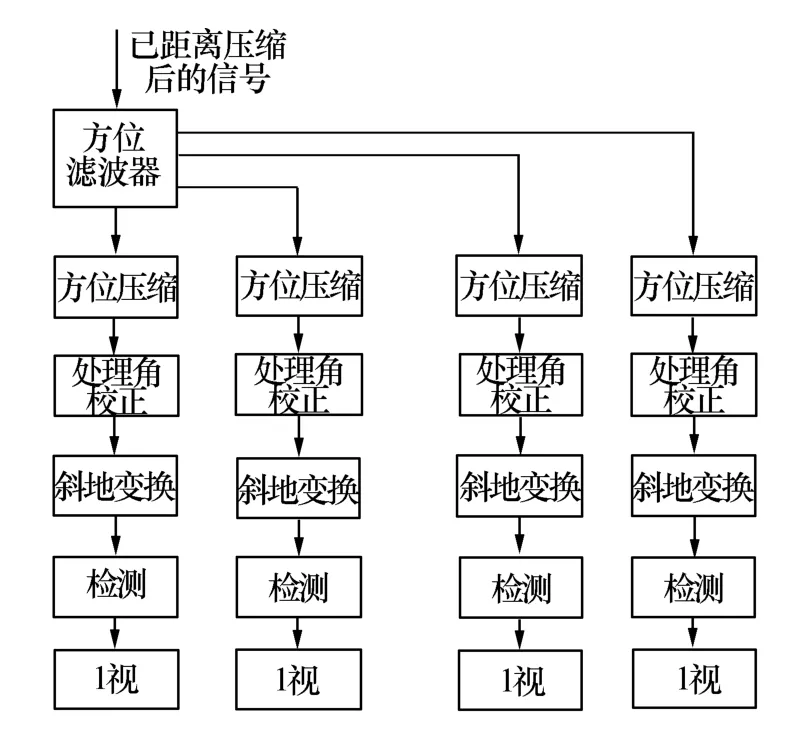
图4 获得多个单视复图像处理

2 高分辨率多基线InSAR高度维成像算法

建立了阵列信号处理模型后，就可以使用相关的信号处理方法进行高度维成像了。二维SAR成像时，方位、距离坐标相同而高度不同的各个点是层叠在一起的，在高度维上没有分辨能力。而在多基线InSAR里面，多个SAR天线在空间中形成了一个阵列，高度不同的各个散射点回波到达阵列的角度互不相同，通过这些不同的角度可以将层叠在一起的各个散射点分辨出来，从而形成高度维的分辨能力，这就是阵列信号处理实现多基线InSAR高度维成像的基本原理。多基线InSAR高度维成像分辨率取决于对散射点回波波达角(DOA)差异的分辨率能力，采用现代信号处理技术，对DOA的估计能够达到极高的精度，因而多基线InSAR可以得到极高的高度维分辨率。

DOA估计有很多种方法，本文中着重讨论多重信号分类(MUSIC)算法，将它应用于多基线InSAR高度维成像中，并将这种算法与业界已有的传统成像算法进行比较。

2.1 MUSIC算法高度维成像原理

现代信号处理方法的一个核心思想是充分利用信号信息的结构特征，而自相关矩阵或自协方差矩阵往往含有丰富的信息特征。对于上节所建的多基线In-SAR高度维成像模型，观测数据的自相关矩阵为Ry=E{y(n)yH(n)}，上标H表示共轭转置。当航线数为K时，它是一个K×K维的矩阵。可对其进行特征值分解，有

式中:λi(i=1，2，…，K)为特征值，并且 λ1＞λ2＞…＞λK;U是特征向量矩阵。在加性高斯白噪声的条件下，有M个特征值大于某个阈值，称为主特征值，或信号特征值;剩下的K-M个小于该阈值，称为次特征值，或噪声特征值。在很多情况下，主特征值和次特征值差异明显，主特征值要明显大于次特征值，并且在大信噪比时，主特征值的个数一般与信源(散射点)的个数相等。将特征向量矩阵U按相应的特征值大小分块，有

S是矩阵U的前M个主特征值对应的特征向量组成的矩阵;G是后K-M个次特征值对应的特征向量组成的矩阵。可以证明［6］

将式(3)代入到式(8)得

即，在M个散射点来波方向满足aH(ω)G=0，而在其他方向aH(ω)G≠0。

将式(9)改写为标量形式，定义函数

作为相应点目标的高度维像。

由式(9)可知，在有目标存在的角度方向上，P(ω)出现峰值，而在没有目标的位置上，P(ω)迅速衰减，形成了高度维的点目标像。让a(ω)中的ω以一定的角度间隔进行搜索，就可以得到全部的目标高度像。

值得注意的是，对成像而言除了分辨率以外，还要关心旁瓣问题。根据式(10)MUSIC法的P(ω)在目标存在的方向上出现峰值，在偏离目标方向时P(ω)会迅速衰减，但最后并不衰减到零，而是取一个有限值。对成像而言，此有限值是一种平均化的背景亮度，它会使图像的对比度下降，成像时可以减去这个值。

2.2 高度维成像处理步骤

将高度维高分辨率成像处理步骤总结如下:

步骤1 常规的二维SAR成像，可以采用RD，CS，ECS等算法，要求校正距离徙动。成像后所有的图像都要精确配准，配准可以采用相干系数法、平均波动函数法、最大干信比法、最小残余点数法等［7］。值得注意的是成像处理器必须存储每一个单视的复图像，而不是存储多视相加后的多视复图像，这一点容易从频域多视处理器上实现。

步骤2 精配准后的K幅N个单视SAR复图像上的每一点，都形成一个K×N维的观测数据矩阵y(n)。

步骤3 求y(n)自相关矩阵Ry=E{y(n)yH(n)}。

步骤4 根据式(10)求一个方位、高度坐标位置的高度维像，可以通过基本干涉相位角变化搜索来实现。成像过程中要减最小值并做归一化处理。

3 数字仿真实验

为了验证阵列信号处理进行高度维成像的性能，本文进行了数字仿真实验。实验中假定天线等间距排列，形成均匀线阵(ULA)，若不均匀，需要将数据插值到均匀栅格再处理。数据的模拟是根据式(2)的模型进行的，这里设噪声为零均值的、独立同分布(IID)的加性高斯白噪声，而且各个视之间也是相互独立的，N视的噪声向量可以通过随机数发生器运行N次来求得。目标信源s(n)可以是各种信源，如高斯信源。在不同的视，它们的值是不同的，为了减小计算量，本文假定信源与视无关，它只是一个确定性的矢量，即假设s(n)=［τ1，τ2，…，τM］T，τi(i=1，2，…，M)是各个散射点的散射强度。这一假设并不影响算法的性质，却可以减小仿真的复杂度。通过上述方法不难得到模拟的观测数据矩阵y(n)，它是一个K×N的矩阵。

MUSIC算法都需要用到观测数据的自相关矩阵Ry=E{y(n)yH(n)}，实际数据是有限的数据，因此只能对Ry进行估计，本文用式(11)估计自相关矩阵

图5所示的是成像区一个透视切面，即一个方位/高度截面，水平方向是方位向，垂直方向是高度向。沿方位向每隔一个方位分辨单元排列一个散射点，共10个散射点，各点在高度向呈阶梯排布，高度间隔为5 m，10个点的高度值为0 m～45 m，如图5b)所示。实验所用的数据为:天线K=8根，N=10个单视，白噪声的方差为=1，信源功率(i=1，2，…，10)，信噪比/=10 dB。

图5 三维层析成像区中的一个透视切面

图6是使用传统的傅里叶变换法和使用MUSIC算法的成像结果。在图中，散射点高度换算成了干涉相位角的大小。

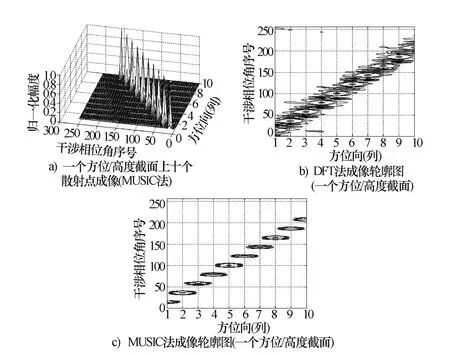
图6 十个散射点的成像结果

为细致观察成像结果，取出方位向第6列像，如图7所示。

图7 传统高度维成像算法与MUSIC成像算法结果比较(K=8，N=10，信噪比 SNR=10 dB)

从图6和图7可以看出，MUSIC算法分辨率远高于传统的DFT方法，而且MUSIC法的峰值旁瓣很低，可低于-30 dB，而传统的DFT的方法第一旁瓣约为-13.2 dB(未加窗)。

再考查分辨率情况，以图7b)中的3 dB宽度作为成像算法的干涉相位角分辨率，使用插值法可以求出两种方法的基本干涉相位角的分辨率分别为:传统DFT法为 φb≈0.715 4 rad=41°，MUSIC 法为 φm≈0.058 9 rad=3.4°，相对于传统DFT法，提高约12倍，分辨率的改善十分显著。

可算得传统DFT法分辨率约为4.55 m，而MUSIC法约为0.38 m，为超分辨，远优于DFT法。

最后再考查积分旁瓣比情况，积分旁瓣比可以通过对图7b)一维冲击响应功率(幅度平方)进行积分得到，定义为［8］

式中:Pmain为主瓣功率;Ptotal为总功率，分子为旁瓣的总能量。

将主要成像性能参数总结如表1所示，表中Pmain计算时把两个相邻零点之间的部分作为主瓣(这时算出来的ISLR比用3 dB宽度作为主瓣时的ISLR典型值要低)。

表1 主要成像性能参数对比(基线数 K=8，视 N=10，SNR=10 dB)

4 结束语

多基线InSAR三维层析成像的关键是高度维成像。由于实际条件的限制，多基线InSAR系统的基线数目通常很少，数据序列的长度很短，采用常规的对观测数据直接进行傅里叶变换的方法难以达到较高的高度维分辨率。本文建立了一个基于阵列信号处理的成像模型，在此模型的基础上，使用阵列信号中的DOA估计算法进行多基线InSAR高度维成像，高度维分辨率大为提高，同时成像旁瓣也很低。

除本文提到的算法外，阵列信号处理中还有许多优良的DOA估计算法，本文没有一一提及，使用这类方法，可以在基线较少的情况下达到很高的高度维分辨率，或者在一定的分辨率要求下只使用很少的基线数。减少一根基线意味着载机少飞行一次，或少一颗小卫星，使得系统简化，成本降低，因此本文提出的成像方法对经济地解决多基线InSAR系统平台的实际困难具有一定的指导意义。

［1］ 王 超，张 红，刘 智.星载合成孔径雷达干涉测量［M］.北京:科学出版社，2002.Wang Chao，Zhang Hong，Liu Zhi.Spaceborne synthetic aperture radar interferometry［M］.Beijing:Science Press，2002.

［2］ Treuhaft R，Moghaddam M，van Zyl J，et al.Estimating vegetation and surface topographic parameters from multibase radar interferometry［C］//Geoscience and Remote Sensing Symposium.Lincoln，NE:IEEE Press，1996:978-980.

［3］ Pasquali P，Prati C，Rocca F，et al.A 3-D SAR experiment with EMSL data［C］//Geoscience and Remote Sensing Symposium.Firenze:IEEE Press，1995:784-786.

［4］ Reigberand A，Moreira A.First demonstration of airborne SAR tomography using multibaseline L-band data［J］.IEEE Transactions on Geoscience and Remote Sensing，2000，38(5):2142-2152.

［5］ 张澄波.综合孔径雷达——原理、系统分析与应用［M］.北京:科学出版社，1989.Zhang Chengbo.Synthetic aperture radar:principle，systems analysis and application［M］.Beijing:Science Press，1989.

［6］ 张贤达.现代信号处理［M］.2版.北京:清华大学出版社，2002.Zhang Xianda.Modern signal processing［M］.2nd ed.Beijing:Tsinghua University Press，2002.

［7］ 柳祥乐，左艳军，杨汝良.基于最少残余点数的InSAR复图像配准［J］. 现代雷达，2007，29(3):37-41.Liu Xiangle，Zuo Yanjun，Yang Ruliang.InSAR SLC based on minimal residues［J］.Modern Radar，2007，29(3):37-41.

［8］ 美 Ian G.Cumming，Frank H.Wong.合成孔径雷达成像——算法与实现［M］.洪 文，胡东辉，等译.北京:电子工业出版社，2007.Ian G Cumming，Frank H.Wong.Digital processing of synthetic aperture radar data:algorithms and implementation［M］.Hong Wen，Hu Donghui，et al，tran.Beijing:Publishing House of Electronics Industry，2007.