采用拉索减震支座的斜拉桥地震易损性分析

钟 剑，庞于涛，沈国煜，袁万城

（同济大学 土木工程防灾国家重点实验室，上海200092）

斜拉桥目前的最大跨径超过1km，对于超大跨度斜拉桥，采用全飘浮体系能够有效地减小地震力，但必须有效地控制地震位移，才能保证整个结构的抗震安全性.在国内外已建成的众多大跨度索支撑桥梁中，已有一些桥梁设置了减小地震位移的装置.例如，日本名港中央大桥在塔梁间设纵向钢线拉索，金门大桥抗震加固中则增设了多个阻尼器；在国内，广东汕头海湾二桥采用钢绞线拉索限位；上海卢浦大桥设置了阻尼器，苏通大桥采用的则是阻尼和限位约束.从以上措施中可以看出，国内外基本上是从增加阻尼和拉索限位2个方面着手来减小地震位移的.

拉索减震支座（专利号CN201530991U）作为一种新型的减隔震支座，由提供耗能的盆式支座与限制墩梁位移的弹性拉索组合而成.研究表明［1-5］，拉索减震支座能够有效地降低桥梁在地震作用下的结构响应.

很多学者都对不同类型的减隔震支座的抗震效果进行过研究［6-8］，但是这些研究大多都是基于确定性，仅仅选用很少的几条地震波作为输入得到结构的响应.由于减隔震支座的有效性很大程度依赖于结构以及地震动的特性，所以确定性的研究很难考虑到结构以及地震的随机性，故不能对结构进行全面的抗震评估［9］.地震动的不确定性以及结构的不确定性导致桥梁结构的地震响应的不确定，因此应从概率的角度对结构的抗震性能进行评价.

地震易损性分析描述桥梁结构在不同水平的地震作用下达到某一极限状态或性能水平的超越概率［10］.通常可以用易损性曲线来表示，它把地震动输入强度（IM）与结构的损伤指标（DI）有机地联系在一起.易损性曲线可以分为经验曲线和理论曲线.经验易损性曲线是基于过去收集到的地震震灾资料应用统计归纳的方法进行地震易损性估计的.文献［11］通过统计1994年Northridge地震的桥梁损伤数据，采用逻辑回归分析建立经验易损性曲线.文献［12］假设易损性曲线可以表示为两参数对数正态分布函数，其参数基于1995年日本Kobe地震中观察到的桥梁损伤数据，通过最大概率方法来计算.

由于震害资料的缺乏以及结构的变化性，经验易损性曲线的应用是有限的.相反，理论易损性曲线在工程和科研中得到越来越多的应用［9］.理论易损性曲线可以通过桥梁结构的地震响应分析得到，可以分为反应谱分析方法［13］、非线性静力分析方法［14］以及非线性时程分析方法［15］.

本文利用塔底弯矩和墩梁相对位移2个损伤指标，通过易损性分析，分别得到构件的易损性曲线；比较全飘浮体系和在塔梁间装有拉索减震支座的斜拉桥的易损性曲线来评价拉索减震支座的减震性能，为合理的抗震设计以及加固提供依据.

1 拉索减震支座

在中小地震作用下依靠支座阻尼耗能来减小地震力，在大震下通过限位装置来限制梁墩的过大位移［16］，正是基于这一思想，在盆式支座以及弹性拉索这2种十分常见装置的基础上，同济大学袁万城教授［1］开发了一种新型的减隔震支座——拉索减震支座（CSFAB），其构造图和实物图分别见图1和图2.

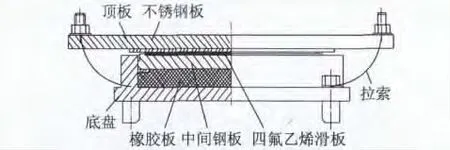
图1 拉索减震支座构造Fig.1 Configuration diagram of CSFAB

图2 拉索减震支座实物Fig.2 Picture of CSFAB

拉索减震支座由盆式支座和拉索两部分主要构件组成，其恢复力模型曲线（图3）也由盆式支座和拉索的恢复力曲线组成.其中，K1为盆式支座的初始刚度，Fs为临界摩擦力，Fs=μN，μ为滑动摩擦系数，N为竖向压力；K2为拉索刚度；u0为弹性拉索的松弛度.

图3 恢复力模型Fig.3 Restoring force model

拉索减震支座的拟静力试验在同济大学2 000t动、静电液伺服加载系统上进行，从其滞回曲线（图4）可以看出，摩擦耗能段滞回曲线饱满，耗能稳定，当支座位移超过拉索松弛度时，拉索拉紧，防止过大位移产生，起到良好的限位作用.通过分析本文设置u0=5cm，K2=7×105kN·m-1，μ=0.02.

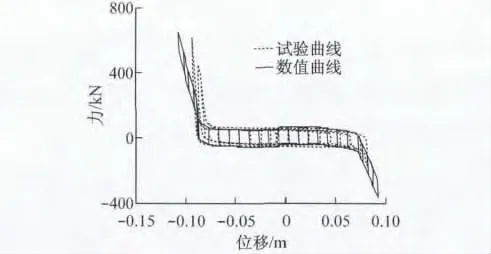
图4 拉索减震支座的试验与数值滞回曲线Fig.4 The test and numerical hysteresis curves of CSFAB

2 概率地震需求模型

简单地说，易损性曲线可以描述为在给定的IM下结构的需求（D）超出其能力（C）的条件概率［17］，计算公式如下：

式中：D通过建立有限元模型计算得到，C通过定义DI和结构的极限状态（LS）计算得到.

增量动力分析（IDA）方法和概率地震需求分析（PSDA）［18］是概率需求地震模型（PSDM）的2种常用方法.在IDA分析方法中，IM情况下的损伤概率由式（2）给出：

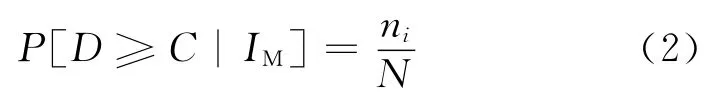
式中：ni为破坏状态i出现的数目；N为指定IM下所有的模拟工况的数目.由于IDA曲线的形成需要很多个分析点，所以IDA分析方法需要更多的计算消耗.

从计算效率出发，本文采用PSDA方法.PSDA方法中，假定地震需求Sd与IM为对数线性相关［19］.

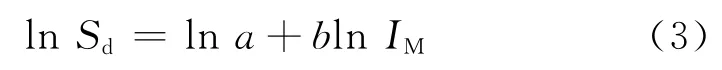
式中：a，b为线性拟合系数.

假定在给定的IM下，lnSd为正态分布［18］，标准差可以表示为

式中：Φ（·）为标准正态分布函数.

2.1 地震动选取以及地震动强度指标

本文研究的桥梁所在的区域为中软场地土，场地类别为III类.从 PEER（Pacific Earthquake Engineering Research Center）强震记录数据库选取30条III类场地地震波，这些波的震级为6.0～6.7，地面峰值加速度（aPGA）为0.068～0.877.从图5a中可以看出aPGA大于0.7的地震动非常少，大部分地震动的aPGA分布在0～0.4之间.文献［9］在对选择的250条地震波的aPGA分析中指出：由于输入地震动aPGA都偏小，这种不平衡性可能会在PSDA方法的计算中带来很大的误差.为了尽可能减小由于计算方法带来的误差，本文对地震波进行调幅，使得30条地震波的aPGA服从0～1均匀分布.从图5b可以看出，调幅后的地震波aPGA分布较为均匀.图6给出了调幅后的阻尼比为5%的各条地震波的谱加速度曲线以及平均谱加速度曲线.

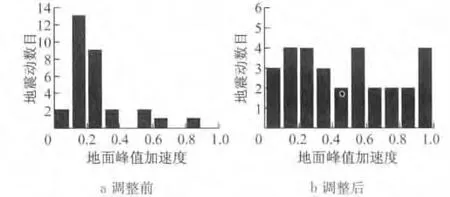
图5 30条波的地面峰值加速度分布Fig.5 PGA distribution of 30waves

图6 地震波反应谱Fig.6 Response spectrums

地震动可以通过aPGA、峰值速度、谱加速度等强度指标来描述［20］.文献［21］建议，概率分析结果的线性一致性可以作为IM能否应用的判断标准.基于此标准，aPGA和峰值速度都是IM的比较好的选择.文献［22］对IM的效率、可适用性以及危害的可计算性进行分析，结果表明：aPGA是比较合适的地震动强度指标.因此，本文选择aPGA作为地震动强度指标研究在纵向地震作用下桥梁结构的响应.

2.2 损伤指标

从以往的斜拉桥地震震害中可以发现，斜拉桥塔底弯矩和主梁的相对位移过大是2个主要的破坏形式.主塔是斜拉桥最主要的承重构件，其损伤程度决定了斜拉桥结构的大部分损伤情况，也是判断斜拉桥整桥是否安全与可靠的关键所在［23］，所以本文选取主塔塔底的弯矩以及辅助墩处的墩梁相对位移作为2个主要的损伤指标.

斜拉桥桥塔是轴压比较大的高塔结构，进入非线性以后的抗震能力以及破坏形式人们还没有统一的认识，故对塔底弯矩本文只考虑一个性能状态，认为当其超过等效屈服弯矩后桥塔即发生完全损伤.塔底弯矩损伤指标采用等效屈服弯矩，等效屈服弯矩的计算见2.3节.

鉴于斜拉桥墩梁相对位移损伤状态的复杂性，国内外没有太多的文献对其进行明确的定义，故本文借鉴焦驰宇［24］对大跨度斜拉桥辅助墩处墩梁位移损伤状态的阐述，具体定义见表1.表中d1为墩梁相对位移大小，dc为支座设计允许位移大小，du为梁端到墩顶内侧的纵桥向水平距离.

表1 墩梁相对位移纵桥向损伤指标Tab.1 Damage indexes of longitudinal pier-girder relative displacement

2.3 斜拉桥模型

某斜拉桥采用独塔双索面体系，跨径布置为55 m+2×165m+55m=440m.斜拉桥主塔顶至桥面高81m.主梁为π形与箱形组合型式梁，主跨为箱形预应力混凝土梁，边跨为π形预应力混凝土梁，支点处梁高3.955m，跨中梁高2.468m.全桥共设有斜拉索56根，以塔为中心对称布置，立面上为14对，每对共4根，每根斜拉索相互平行，仰角29°，梁上索距8m，塔上索距4.434m.斜拉桥结构示意图如图7，其中P1-P5为墩号.工况1采用全飘浮体系，塔梁间不设支承，边墩及辅助墩上设纵向滑动支座.为了能够有效地控制梁端位移以及主塔底部弯矩，工况2在塔梁间设置安装拉索减震支座.

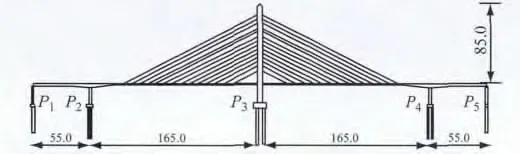
图7 斜拉桥结构示意（单位：m）Fig.7 Structure diagram of a cable-stayed bridge（unit：m）

采用SAP2000通用有限元分析软件建立该斜拉桥有限元分析模型.在有限元模型中，主梁、主塔、墩均采用梁单元模拟；斜拉索采用梁单元模拟，并运用Ernst公式考虑索因自重导致的垂度效应所造成的弹性模量的折减，采用6弹簧体系模拟桩-土相互作用，支座采用图3的力学模型进行模拟.

塔底截面见图8a，使用Ucfyber软件计算其弯矩曲率曲线（见图8b），其等效屈服弯矩为4.0×105kN·m.

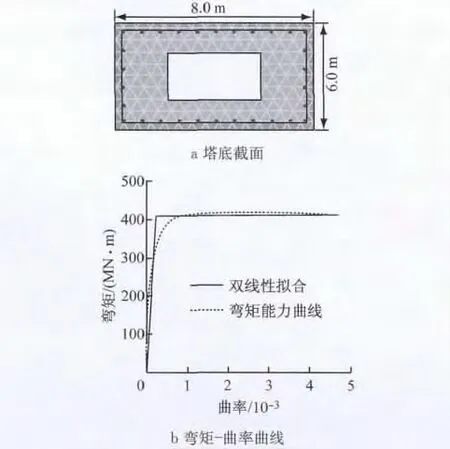
图8 塔底截面及弯矩-曲率曲线Fig.8 Section and M-φcurves of tower base

3 斜拉桥易损性分析

3.1 概率地震需求模型曲线

图9给出了安装拉索减震支座前后的斜拉桥的PSDM的对数线性拟合，分别以塔底弯矩（M）和墩梁相对位移（δ）为工程需求参数（EDP）.由式（3）可以得到a和b，由式（4）可以得到标准差.安装拉索前后的塔底弯矩以及墩梁位移对数线性拟合的参数见表2.

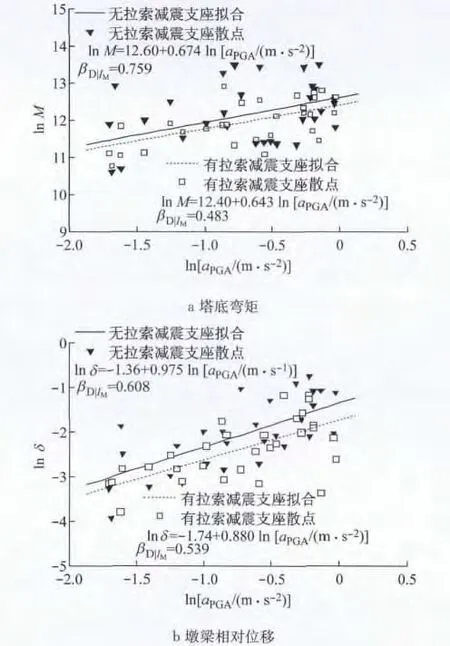
图9 安装拉索减震支座前后的斜拉桥概率地震需求模型曲线Fig.9 PSDMs with or without CSFAB

表2 安装拉索减震支座前后的拟合曲线参数对比Tab.2 Comparison of the PSDMs with or without CSFAB

从图9以及表2可以看出，安装拉索减震支座以后，对数线性回归曲线的均值（式（3））以及标准差（式（4））都发生了变化.比如在安装拉索减震支座前后，塔底弯矩的对数标准差从0.759减小到0.483，墩梁位移的对数标准差从0.608降低至0.539.意味着拉索减震支座可以降低结构在地震作用下的离散性，增加结构在地震作用下响应的稳定性.

安装拉索减震支座以后，塔底弯矩和主梁的位移都减小，其中塔底弯矩下降的幅度较小，而主梁位移则有比较明显的减小.

3.2 损伤曲线

由式（5）可以计算出各个构件不同损伤程度的易损性方程，其曲线见图10.对于4种损伤状态，和全飘浮体系相比（图10a），安装拉索减震支座以后（图10b）墩梁相对位移减小比较多，表现为其损伤概率都大幅度降低.为了进一步比较，将拉索减震支座安装前后的墩梁相对位移的中等损伤和完全损伤的易损曲线放在同一坐标轴下进行对比（图11a），可以看出，墩梁相对位移显著减小.对比塔底弯矩可以看出安装拉索减震支座也可以在一定程度上降低主塔塔底弯矩的易损性（图11b）.

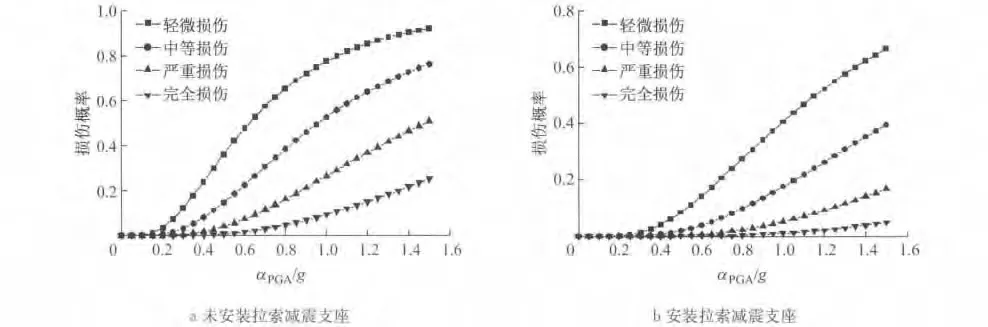
图10 墩梁相对位移的易损性曲线Fig.10 Fragility curves of pier-girder displacement

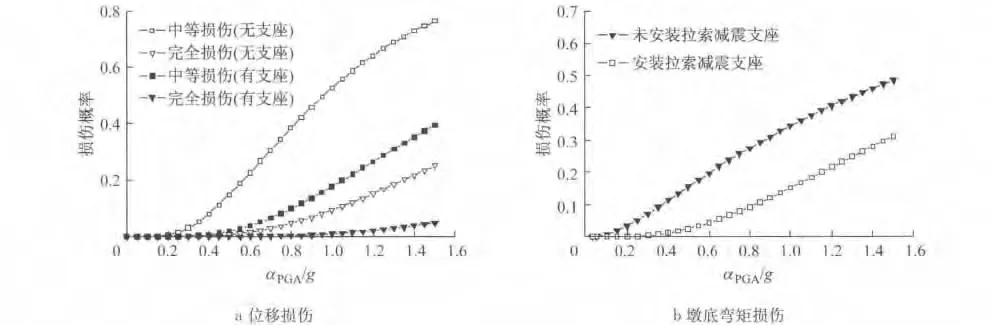
图11 安装拉索减震支座前后的斜拉桥易损性曲线Fig.11 Comparison of fragility curves between cable-stayed bridges with or without CSFAB

3.3 结果讨论

从图11可知，在塔梁间安装拉索减震支座以后，主塔弯矩和墩梁位移都有不同程度的减小，由讨论以及参数分析可知，在斜拉桥塔梁连接处安装拉索减震支座后各构件损伤概率的降低主要归结于以下2个方面.

3.3.1 阻尼

盆式支座的摩擦耗能可以增加斜拉桥的结构阻尼，通过反应谱曲线可以看出（图12），结构阻尼的增加可以在减小地震力的同时减小墩梁的相对位移.

3.3.2 传力路径

梁塔间设置弹性拉索后斜拉桥的纵向刚度增加，纵飘周期减小.从图12可以看出，减小周期可以减小主梁的位移，但是会增加地震力.图6表明，对于斜拉桥等长周期结构，在如图周期大于2s的范围里减小固有周期仅会使地震力有较小幅度的增加.

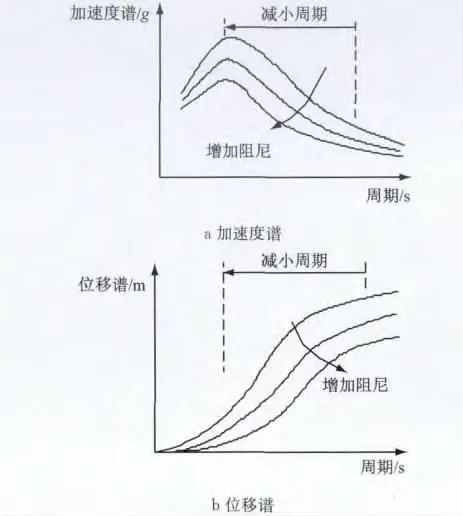
图12 反应谱曲线Fig.12 Response spectrums curves

对于斜拉桥这种塔高臂长的结构，影响塔底弯矩除了地震力之外，力臂的长度也是一个重要因素.对于全飘浮体系斜拉桥，地震力通过斜拉索全部传到主塔顶部（图13），力臂（h2）很大；设置弹性拉索之后，地震作用下主梁的惯性力（F2）一部分通过斜拉索传到塔顶，另一部分地震力（F1）则通过弹性拉索传到梁塔处，这样，力臂（h1）就会大大减小.而F1，F2的相对大小由塔梁间设置的弹性拉索刚度K决定，这样通过合理选择拉索刚度既可以减小主梁的位移，又可以降低塔底的弯矩.

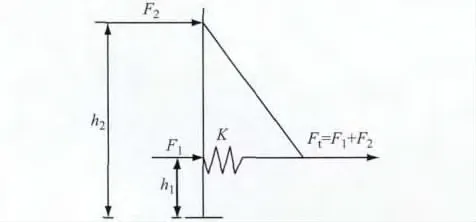
图13 斜拉桥地震力的传力路径Fig.13 Seismic force transferring path of cable-stayed bridges with CSFAB

利用图6的30条地震波的平均反应谱曲线进行拉索刚度的参数敏感性分析，以全飘浮体系斜拉桥为参考，得到不同弹性拉索刚度下的斜拉桥的塔底弯矩以及主梁位移的归一化响应.

图14中RM，RD分别为安装拉索减震支座后与安装前的塔底弯矩比值、墩梁相对位移的比值.从图14可以看出，当弹性拉索的刚度值小于8×105kN·m-1时，塔底弯矩小于全飘浮体系斜拉桥的值，当刚度值约为5×105kN·m-1时，塔底弯矩值最小；同时主梁的位移在此刚度范围内减小得很快.综合考虑位移和弯矩两方面响应，选取刚度为5×105～8×105kN·m-1（本例为7×105kN·m-1），既可以降低塔底的弯矩，又可以减小墩梁之间的位移.

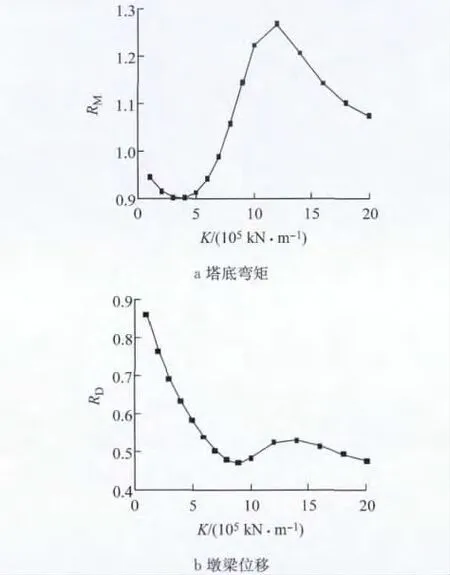
图14 拉索刚度对斜拉桥响应的影响Fig.14 Seismic response for various elastic cables stiffness

4 结论

以概率地震需求分析为基础建立了某斜拉桥有无拉索减震支座的非线性动力模型，得到斜拉桥的塔底弯矩以及梁墩相对位移的易损性曲线.

（1）安装拉索减震支座以后，结构响应在地震作用下的标准差βD｜IM有所降低，这意味着拉索减震支座可以降低结构在地震作用下的离散性，增加结构在地震作用下响应的稳定性.

（2）对比安装拉索减震支座前后的塔底弯矩以及主梁位移的易损性曲线可以看出，安装拉索减震支座可以有效地降低塔底弯矩和主梁位移，降低二者在地震作用下的损伤概率.

（3）拉索减震支座的2个构件即盆式支座和弹性拉索分别增加了结构的阻尼和改变了斜拉桥在地震作用下的惯性力传力路径，从而达到了降低结构响应的目的.

（4）对弹性拉索刚度进行参数敏感性分析可以发现，弹性拉索的刚度在5×105～8×105kN·m-1范围内是一个优化的值.

［1］ 袁万城，曹新建，荣肇骏.拉索减震支座的开发与试验研究［J］.哈尔滨工程大学学报，2010，31（12）：1593.YUAN Wancheng，CAO Xinjian，RONG Zhaojun.Development and experiment study on cable-sliding friction aseismic bearing［J］.Journal of Harbin Engineering University，2010，31（12）：1593.

［2］ Wei Z H，Yuan W C，Cheung P C.Seismic performance of continuous girder Bridges using cable-sliding friction aseismic bearing［J］.Procedia Engineer，2011，14：914.

［3］ Yuan W C，Wang B B，Cheung P.Seismic performance of cable-sliding friction bearing system for isolated bridges［J］.Earthquake Engineering and Engineering Vibration，2012，11（2）：173.

［4］ 袁万城，王斌斌.拉索减震支座的抗震性能分析［J］.同济大学学报：自然科学版，2011，39（8）：1126.YUAN Wancheng，WANG Binbin.Numerical model and seismic performance of cable-sliding friction aseismic bearing ［J］.Journal of Tongji University：Natural Science，2011，39（8）：1126.

［5］ 袁万城，韦正华，曹新建.拉索减震支座及桥梁抗震设计应用研究［J］.工程力学，2011，28（S2）：204.YUAN Wancheng，WEI Zhenghua，CAO xinjian.Cable-sliding friction aseismic bearing and its application to bridge seismic design［J］.Engineering Mechanicis，2011，28（S2）：204.

［6］ Jangid R.Optimum friction pendulum system for near-fault motions［J］.Engineering Structures，2005，27（3）：349.

［7］ Jangid R.Optimum lead-rubber isolation bearings for near-fault motions［J］.Engineering Structures，2007，29（10）：2503.

［8］ Sharabash M A，Andrawes O B.Application of shape memory alloy dampers in the seismic control of cable-stayed bridges［J］.Engineering Structures，2009，31（2）：607.

［9］ Zhang J，Huo Y L.Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method［J］.Engineering Structures，2009，31（8）：1648.

［10］ Choi E S，DesRoches R，Nielson B.Seismic fragility of typical bridges in moderate seismic zones［J］.Engineering Structures，2004，26（2）：187.

［11］ Basöz N I，Kiremidjian A S，King S A.Statistical analysis of bridge damage data from the 1994 Northridge，CA，Earthquake［J］.Earthquake Spectra，1999，15（1）：25.

［12］ Shinozuka M，Feng M Q，Lee L.Statistical analysis of fragility curves［J］.Journal of Engineering Mechannics，ASCE，2000，126（12）：1224.

［13］ Hwang H，Jernigan J，Lin Y.Evaluation of seismic damage to memphis bridges and highway systems［J］.Journal of Bridge Engineering，2000，5（4）：322.

［14］ Shinozuka M，Feng M Q，Kim H K.Nonlinear static procedure for fragility curve development［J］.Journal of Engineering Mechanics，ASCE，2000，126（12）：1287.

［15］ Karim R K，Yamazaki F.A simplified method of constructing fragility curves for highway bridges［J］.Earthquake Engineering and Structure Dynamics，2003，32（10）：1603.

［16］ Desroches R，Smith B.Shape memory alloys in seismic resistant design and retrofit：a critical review of their potential and limitations［J］.Journal of Earthquake Engineering，2004，8（3）：415.

［17］ Padgett E J，DesRoches R.Methodology for the development of analytical fragility curves for retrofitted bridges［J］.Earthquake Engineering and Structure Dynamics，2008，37（8）：1157.

［18］ Baker W J.Vector-valued ground motion intensity measures for probabilistic seismic demand analysis［J］.Stanford：Stanford University，2005.

［19］ Cornell C A，Jalayer F，Hamburger O R.Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines［J］.Journal of Structure Engineering，ASCE，2002，128（4）：526.

［20］ Mackie K，Stojadinovic B.Performance-based seismic bridge design for damage and loss limit states［J］.Earthquake Engineering and Structure Dynamics，2007，36（13）：1953.

［21］ Mackie R K.Fragility basis for California highway overpass bridge seismic decision making［D］.Berkeley：University of California，Berkeley，2005.

［22］ Padgett E J，Nielson G B，DesRoches R.Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios［J］.Earthquake Engineering and Structure Dynamics，2008，37（5）：711.

［23］ 冯清海.特大桥梁地震易损性与风险概率分析［D］.上海：同济大学，2008.FENG Qinghai.Study on seismic vulnerability and risk probability analysis of super-large bridge［D］.Shanghai：Tongji University，2008.

［24］ 焦驰宇.基于性能的大跨斜拉桥地震易损性分析［D］.上海：同济大学，2008.JIAO Chiyu.Performance based seismic fragility analysis of longspan cable-stayed bridges［D］.Shanghai：Tongji University，2008.