斯蒂芬逊型六杆机构运动分析与仿真

周 涛，余智慧，李亮亮，李 妍，梁洪濯，李 双

斯蒂芬逊型六杆机构运动分析与仿真

*周 涛1，余智慧2，李亮亮1，李 妍1，梁洪濯1，李 双1

（1.安徽工业大学机械工程学院，安徽，马鞍山 243032； 2.合肥工业大学继续教育学院，安徽，合肥 230009）

采用解析法推导斯蒂芬逊型六杆机构各杆件的位移、速度和加速度表达式，并将其转化为适用于MATLAB 仿真的矩阵数学模型。运用MATLAB/Simulink软件中Embedded MATLAB Function模块编写该机构中速度矩阵的M函数并结合其它模块对其进行运动学仿真。通过Simulink仿真可以获得该机构的运动曲线，直观地描述了机构的运动规律并为其动力学设计部分提供依据。

斯蒂芬逊型六杆机构；MATLAB/Simulink；运动学仿真

机构运动分析是机构运动学设计的基础，并为机构动力学的设计提供依据。机构的运动分析可以获得机构中某些构件的位移、角速度和角加速度，以及某些点的轨迹、速度和加速度。通过机构运动分析可以检查机构是否符合装配及运行要求，如果机构的结构类型及尺度需要修改，则这个设计过程始终贯穿着机构的运动分析[1]。

机构运动分析的方法很多，主要有图解法和解析法[2]。图解法比较直观简单，但精度不高；解析法精度较高，但计算比较繁琐。随着计算机技术的发展，解析法已经被广泛应用。采用解析法并借助计算机，不仅可以获得很高的计算精度以及一系列位置的分析结果，并能绘制出机构相应的运动曲线图，同时还可以把机构分析和机构综合问题联系起来，以便机构的优化。

Matlab是一种面向科学与工程计算的高级语言，它提供了强大的矩阵处理和绘图功能。而Simulink是基于MATLAB的一个交互式动态系统建模、仿真和分析的工具，它具有高性能的科学计算能力，被广泛应用于线性、非线性、离散、连续及多变量系统的仿真和分析[3]。Matlab/Simulink在机械工程中应用较为广泛，可以直观地描述机构的运动规律，为机械虚拟化设计提供方便。

斯蒂芬逊型六杆机构在机械设计中应用比较广泛，特别是在纺织机构中[4]。本文以斯蒂芬逊型打纬机构为例，采用解析法对机构运动进行分析，并运用Simulink软件中Embedded MATLAB Function模块只需编写该机构中速度矩阵的M函数并结合其它模块就能对其进行运动学仿真，得到了相应的运动变化曲线。与文献[4,8]中的仿真方法相比，该方法大大简化了仿真步骤。

1 斯蒂芬逊型六杆机构运动分析

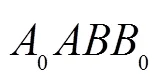
图1 斯蒂芬逊型六杆机构

1.1 建立矢量模型

斯蒂芬逊型六杆函数机构向量模型如图2所示，各构件视为杆矢量。

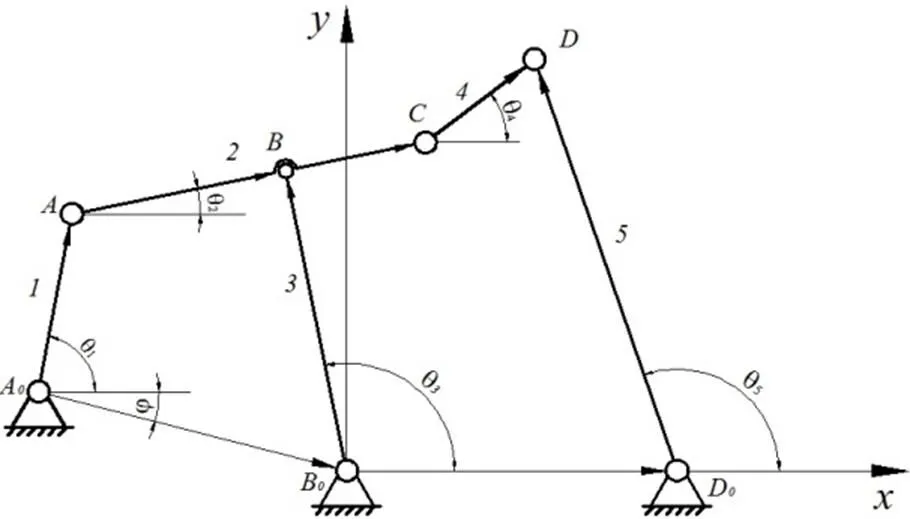
图2 斯蒂芬逊型六杆机构向量模型

1.2 位移分析

斯蒂芬逊型六杆函数机构的闭环矢量方程为：

将式（1）、（2）复数表示为：

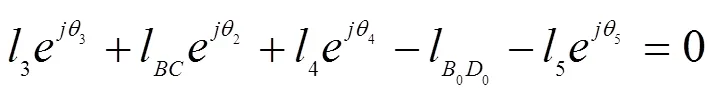
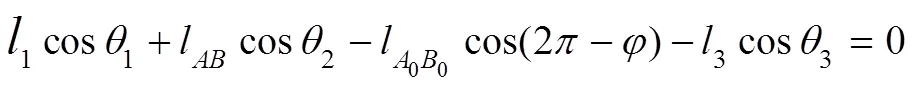
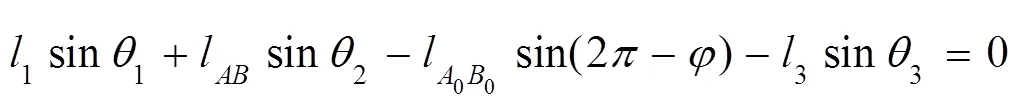
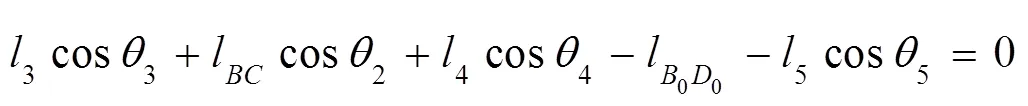
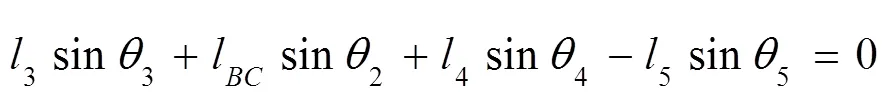
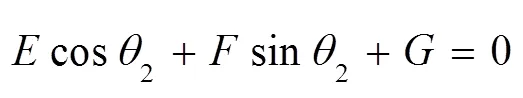
式中：

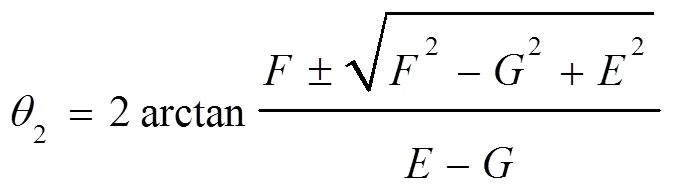
式中根号前“+”适用于构件2逆时针转动，“—”适用于构件2顺时针转动[7]。

取

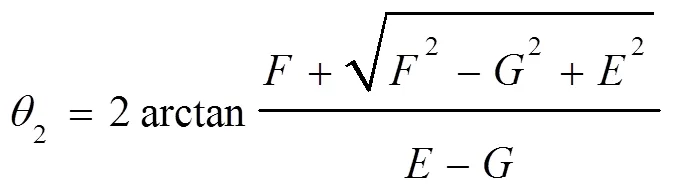
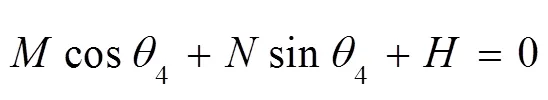
式中：

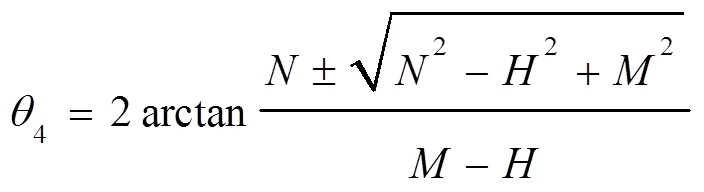
式中根号前“+”适用于构件4逆时针转动，“—”适用于构件4顺时针转动。

取

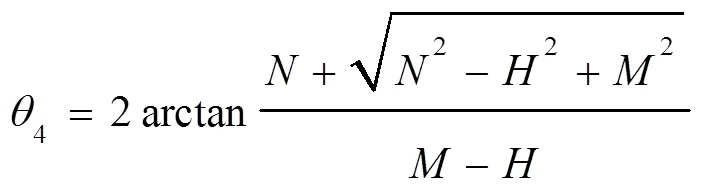
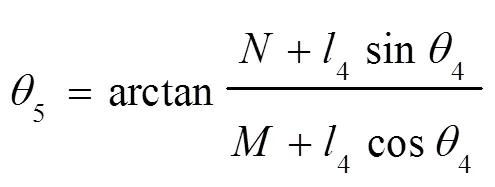
1.3 速度分析

将式（5）~（8）分别对时间一阶求导，得：

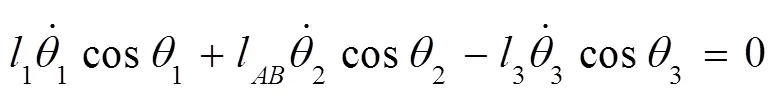
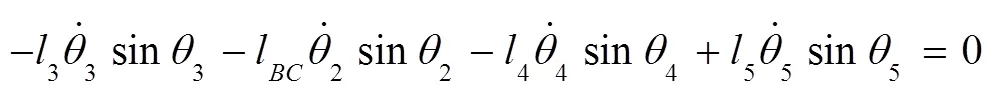
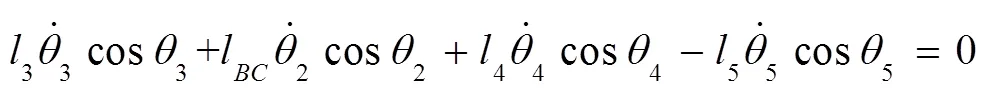
将（17）~（20）写成矩阵的形式为：

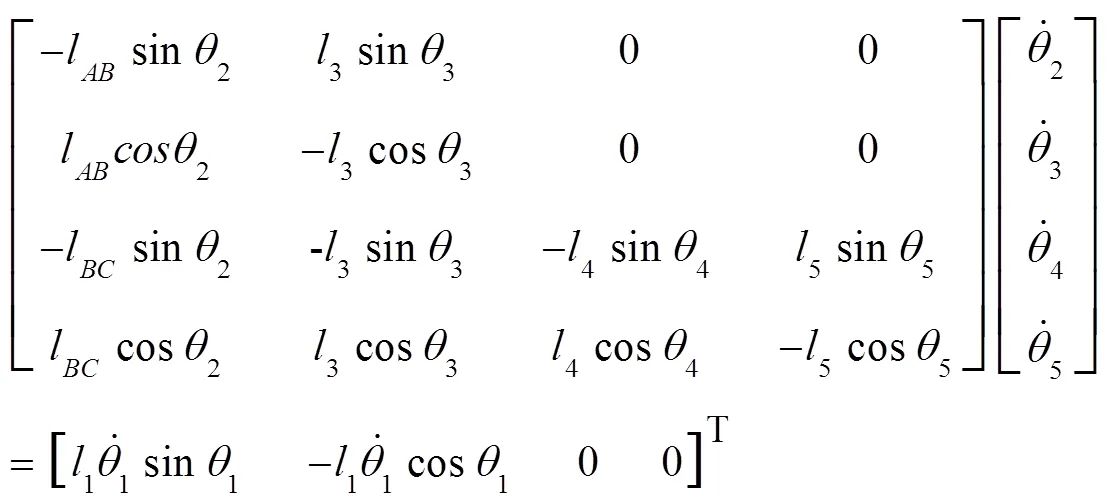
1.4 加速度分析

将式（5）~（8）分别对时间二阶求导，得：

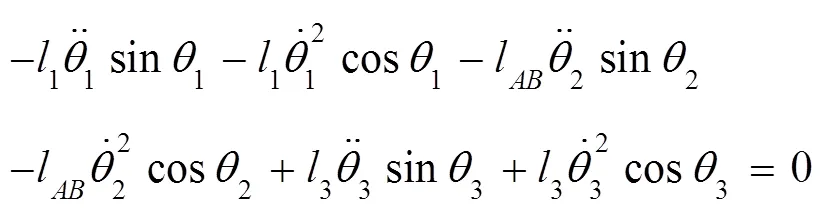
将（22）~（25）写成矩阵的形式为：

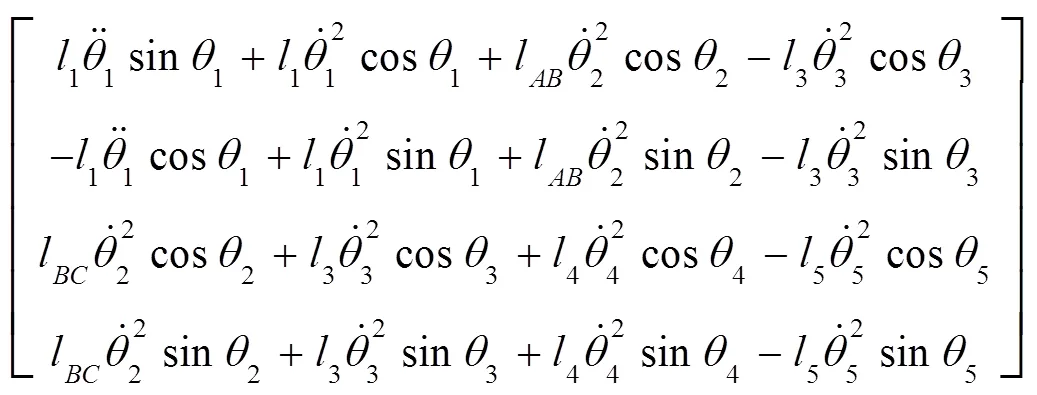
2 斯蒂芬逊型六杆函数机构运动学仿真

2.1 斯蒂芬逊型六杆函数机构运动学仿真模型

本文结合斯蒂芬逊型六杆打纬机构进行仿真，该机构的仿真模型如图3所示。根据前面建立的数学模型，运用MATLAB/Simulink软件中Embedded MATLAB Function函数模块编写式（17）~（20），该函数的输入参量为各构件的角位移量以及构件1的角速度量，输出参量为构件2、构件3、构件4及从动件5的角速度量。在此基础上，利用积分模块对各构件的角速度分别进行积分，求得其对应的角位移量，再对利用微分模块对各构件的角速度分别进行微分，求得其对应的加速度量。所求的变量通过To Workplace模块将数据写入工作空间中的simout1、simout2和simout3变量。

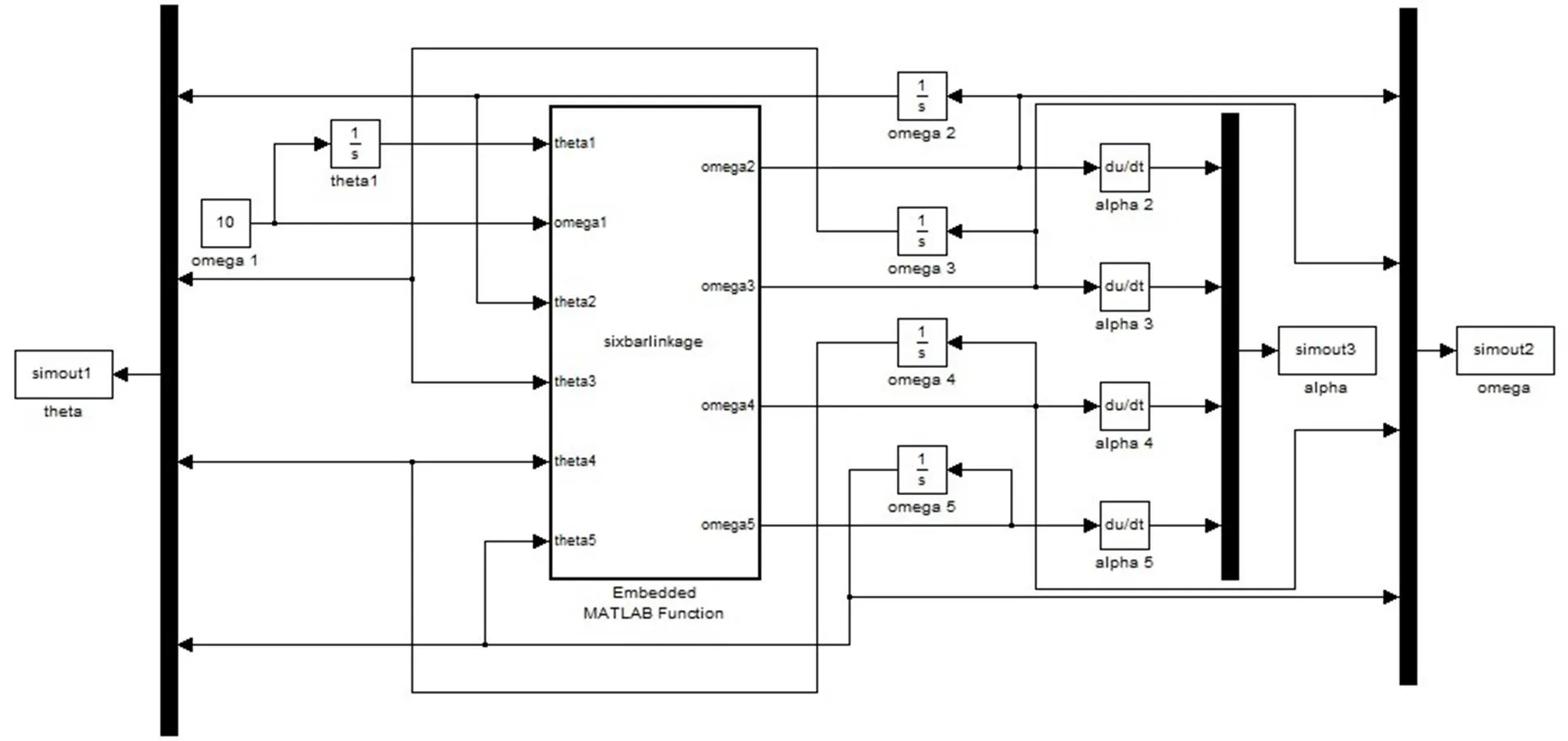
图3 斯蒂芬逊型六杆机构的仿真模型

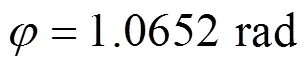
2.2 斯蒂芬逊型六杆机构运动仿真结果与分析

采用ode113（adams）变步长算法，设定最大积分步长(Max step size)为0.01[8]。积分模块的初值设置为0，构件1初始角为0和角速度为10 rad/s逆时针方向回转，因此每转动一周的时间是T=0.628 s，设置仿真时间为1 s，即仿真初始时间(start time)设为0，终止时间(stop time)设为1。

仿真结果由工作空间变量simout1、simout2和simout3模块输出，用绘图命令绘制出各杆件的位置、角速度和角加速度如图4～图15所示。

图4 构件2的角位移

Fig.4 Angular displacement of link 2

图5 构件3的角位移

Fig.5 Angular displacement of link 3

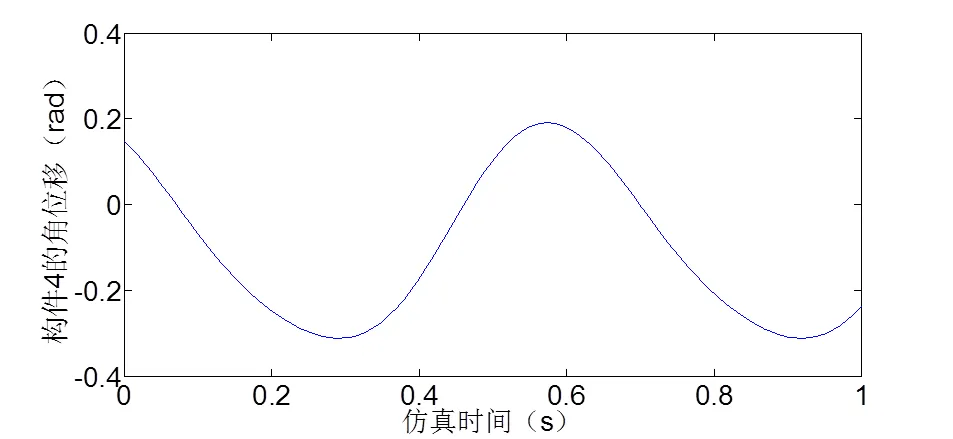
图6 构件4的角位移

Fig.6 Angular displacement of link 4

图7 构件5的角位移

Fig.7 Angular displacement of link 5

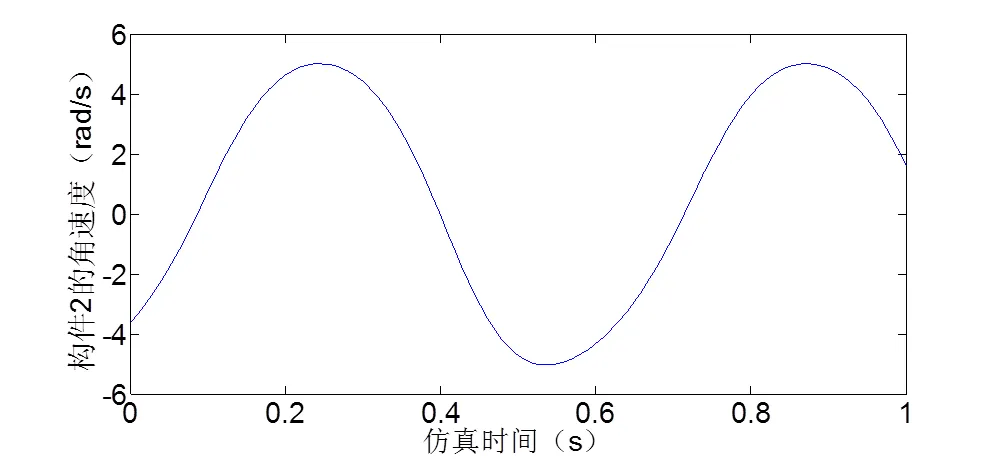
图8 构件2的角速度

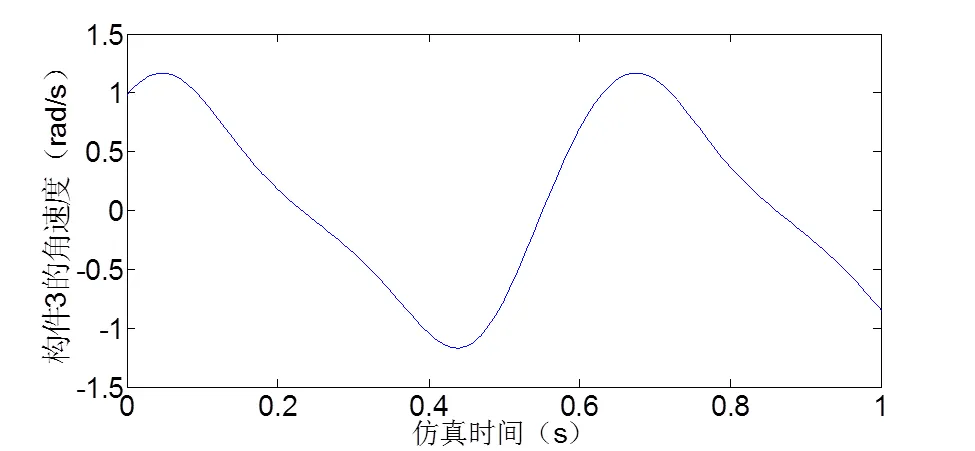
图9 构件3的角速度

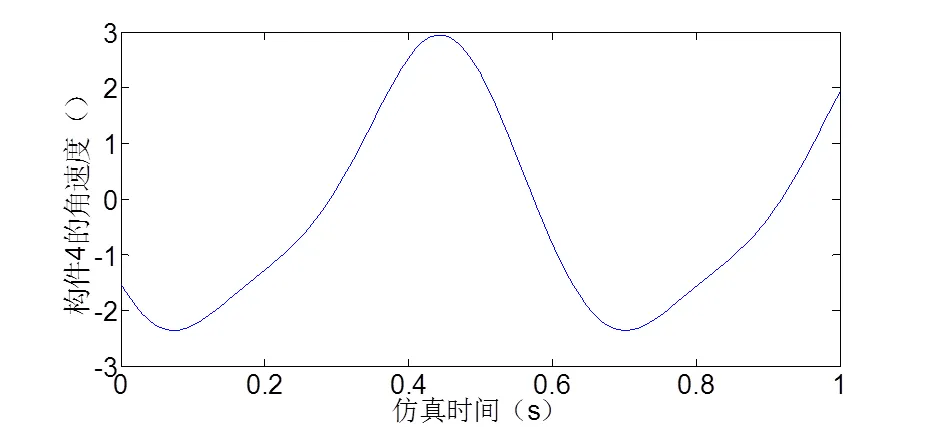
图10 构件4的角速度

图11 构件5的角速度

图12 构件2的角加速度

图13 构件3的角加速度

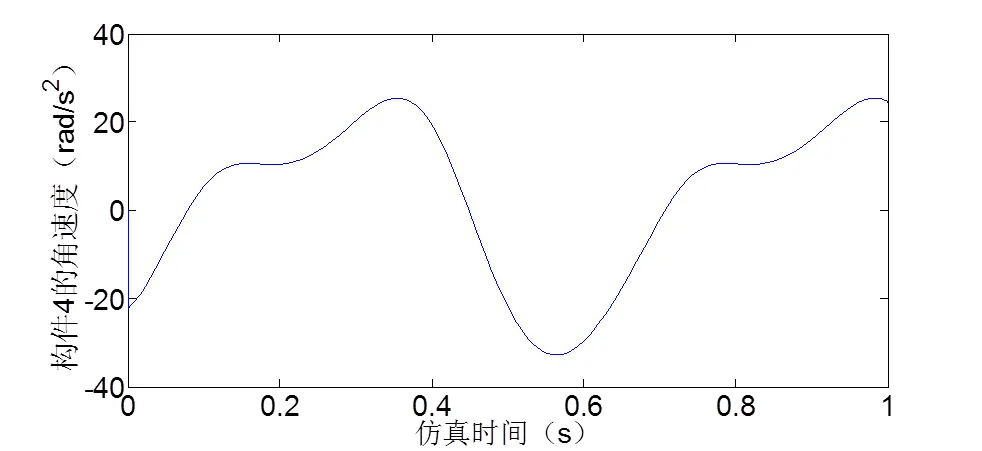
图14 构件4的角加速度

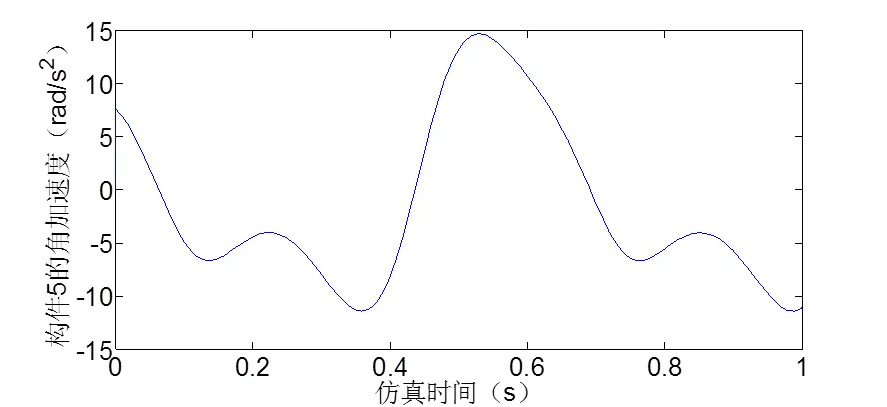
图15 构件5的角加速度

由Matlab/Simulink分析的结果可以得出：

1）构件2、构件3、构件4、构件5的角位移、角速度和角加速度呈规律性变化，各杆件在铰接处运动曲线过渡平滑，不存刚性冲击。

2）一个周期内，构件3和构件5的角位移、角速度和角加速度的变化幅值分别小于构件2和构件6的角位移、角速度和角加速度的变化幅值。

4）通过仿真得到的运动曲线图，可以识别和分析机构的运行情况，找到设计的不足之处。通过本例也可以从侧面体现机构仿真的意义。

3 总结

[1] 曹惟庆,徐曾萌.机构设计[M].北京：机械工业出版社,1999.

[2] 孙恒,陈作模,葛文杰.机械原理[M].7版.北京：高等教育出版社,2006.

[3] Robert L.Norton. An introduction to the synthesis and analysis of mechanisms and machines [M]. Beijing: China Machine Press, 2006.

[4] Gordon R. Pennock, Ali IsrarKinematic. Analysis and synthesis of an adjustable six-bar linkage[J]. Mechanism and Machine Theory, 2009(44) :306-323.

[5] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2011.

[6] 蒋洪潮,胡旭东.连杆打纬机构的运动分析与比较[J].浙江丝绸工学院学报,1988(4):44-48.

[7] Meng Caifang , Zhang Ce.Optimal design and control of a novel press with an extra motor[J].Mechanism and Machine Theory, 2004,39:811-818.

[8] 曲秀全,焦映厚,陈照波.RPR- RPP六杆机构的MATLAB运动学仿真[J].机械科学与技术,2003(7):132-135.

[9] 宋叶志,贾东永.MATLAB数值分析与应用[M].北京：机械工业出版社,2009.

Kinematic Analysis and Simulation of a Stephenson Six-Bar Linkage

*ZHOU Tao1，YU Zhi-hui2，LI Liang-liang1，LI Yan1，LIANG Hong-zhuo1，LI Shuang1

（1. School of Mechanical Engineering, Anhui University of Technology ,Ma’anshan,Anhui 243032, China；2. School of Continuing Education, Hefei University of Technology ,Hefei, Anhui 230009, China）

We derives the formulations of displacement, velocity and acceleration of each bar for a six-bar Stephenson linkage by using analytic method. Furthermore, the formulations are converted into the mathematical models in matrix form which can be applied to the MATLAB simulation. The Embedded MATLAB Function module in MATLAB/Simulink can compile M function of velocity matrix and combine with other modules carrying on kinematic simulation of this mechanism. We can not only obtain motion curves and kinematic equations of mechanism directly, but also provide the basis for dynamic mechanism design though Simulink simulation.

six-bar stephenson linkage；MATLAB/Simulink；kinematic simulation

TH113.2+2

A

10.3969/j.issn.1674-8085.2014.02.018

1674-8085(2014)02-0083-06

2014-01-07；

2014-02-06

*周 涛(1987-)，男，安徽安庆人，硕士生，主要从事现代机械设计理论与方法研究(E-mail：zhoutao_87@163.com);

余智慧(1990-)，女，安徽安庆人，主要从事机械设计制造及其自动化研究(E-mail：yuzhihui421@yeah.net);

李亮亮(1989-)，男，安徽淮北人，硕士生，主要从事生物力学研究(E-mail：Sccot31@163.com);

李 妍(1987-)，女，山东滨州人，硕士生，主要从事机器人运动轨迹规划研究(E-mail：a13864892159@163.com);

李 双(1991-)，女，安徽阜阳人，硕士生，主要从事机器人运动轨迹规划研究(E-mail：415879675@qq.com);

梁洪濯(1989-)，男，安徽马鞍山人，硕士生，主要从事生物力学研究(E-mail：lianghongzhuo@163.com).