B2型TiSi合金点缺陷结构和力学性能的第一性原理研究
2014-10-29孙彩红
孙彩红,武 敏,安 博
B2型TiSi合金点缺陷结构和力学性能的第一性原理研究
孙彩红,武 敏,*安 博
(渭南师范学院物理与电气工程学院,陕西,渭南 714099)
采用基于密度泛函理论的第一性原理计算了B2型TiSi合金各种点缺陷结构的晶格常数、形成能、形成热和弹性性质。结果表明:Ti空位缺陷(VTi)和Si反位缺陷(SiTi)的形成能和形成热较小,在合金过程中较易产生;合金缺陷结构具有小的体弹模量和剪切模量;相对TiSi合金完美结构,缺陷结构的韧性较低。
第一性原理;TiSi合金;点缺陷
Ti合金由于其密度小、室温塑性好、耐腐蚀等优点被广泛应用于航空航天、高精度仪器等[1]。根据Ti-Si合金的相图可知Ti-Si之间存在五种稳定化合物:Ti3Si、Ti5Si3、Ti5Si4、TiSi2和TiSi等。文献[2-6]在实验和理论各方面深入探讨了Ti-Si各种化合物的形成机制、合成途径和主要用途,但鲜见对TiSi合金缺陷性能的研究报道。本文采用基于密度泛函理论的第一性原理方法研究了TiSi合金及其点缺陷结构的形成能、形成热和弹性性能,分析了缺陷结构对合金性能的影响。
1 模型和计算方法

计算采用基于密度泛函理论的第一性原理赝势平面波法CASTEP程序包[8]。电子交换关联能取GGA中的PBE[9]形式,原子势函数采用超软赝势。为得到稳定结构采用BFGS方法[10]对各种超胞结构进行几何优化。自洽计算时应用Pulay密度混合法[11],收敛条件设为:总能量小于5.0×10-6eV/atom,每个原子上的力低于0.1e V/nm,公差偏移小于5×10-5nm,应力偏差低于0.02 GPa。

图1 TiSi合金结构示意图 (a) 完美结构;(b) 单空位缺陷;(c) 反位缺陷
2 计算结果及讨论
2.1 TiSi合金及其缺陷结构的基本物性
几何优化后得到TiSi合金平衡晶格常数为0=0.6253 nm与文献[12]报道的实验值0=0.6511 nm基本一致。为考察TiSi合金的形成能力,本研究采用式(1)计算了其合金结合能:

E()表示含有个原子的完整合金体系的总能量,表示TiSi晶胞中A原子浓度,’c(A)和’c(B)分别表示纯金属A和B的结合能。计算得TiSi的合金形成能为-0.125 eV,大的负合金形成能说明其形成能力较强。
2.2 TiSi合金的空位缺陷
采用式(2)和(3)分别计算了2×2×2超胞体系中Ti和Si单空位(VTi、VSi)的形成能和形成热:

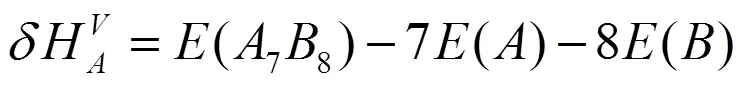
其中A和B分别表示Ti或Si不同原子种类,(78)为缺陷晶体的总能量,(88)为完美晶体的超胞结构的总能量。式(2)中加入单个A原子在理想晶格中的能量()用来弥补体系原子数目不同带来的能量变化。计算结果如表1所示。

表1 TiSi合金缺陷的形成能和形成热(单位:eV)
形成能和形成热为负值意味着合成过程中放热,其值越小说明生成该点缺陷所需能量越低,越容易形成该点缺陷结构。由表1可看出,Ti空位(VTi)形成能和形成热比Si空位(VSi)小,说明相对Si空位,Ti空位更容易形成。特别地,VSi形成能为正值,说明其形成为吸热过程,在合成过程不易产生。
2.2 TiSi合金的反位缺陷
采用式(4)和(5)分别计算了2×2×2超胞体系中Ti和Si反位(TiSi、SiTi)的形成能和形成热:
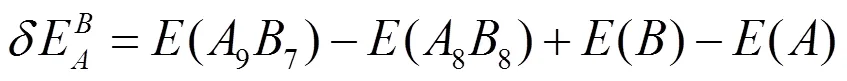
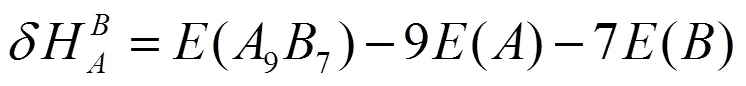
其中(97)为缺陷晶体的总能量,(88)为完美晶体的超胞结构的总能量,()和()分别为与单质晶体平均每个原子的能量。计算结果如表1所示。可知SiTi形成能和形成热比TiSi低,说明合成过程中SiTi放热更多,SiTi缺陷结构更容易形成。
2.3 TiSi合金的弹性性质
衡量平衡晶胞受微小压力时的抗力的一个重要参数为弹性常数,通过总能量随晶格体积的变化——弹性应变能——得到其值[13]。弹性应变能通过式(6)得到:
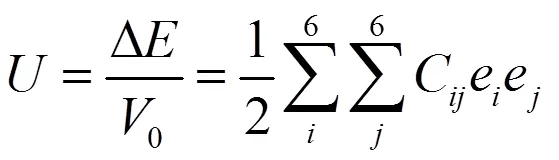
其中△表示能量的变化量,0表示晶胞体积,C表示弹性常数,e和e表示应力。立方晶体具有三个相互独立的弹性常数[14]。TiSi合金及其各种缺陷结构弹性常数的计算值由表2列出。

表2 TiSi合金及其各种缺陷结构的弹性常数(单位:GPa)
为获得稳定结构,C应满足波恩稳定条件[15]。零压下立方晶体的稳定条件由式(7)表示:
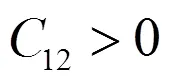
结合表2可以得到,VTi和SiTi结构的弹性常数满足波恩条件能够在零压下稳定存在,这与缺陷形成能和形成热分析结果一致。
弹性常数C、体弹模量、剪切模量、杨氏模量和泊松比都是描述材料机械性能的重要参数。采用Voigt-Reuss-Hill(V-R-H)近似[16]估算多晶结构的机械性能。


表3列出TiSi合金及其缺陷结构弹性系数的计算值。可以看出,TiSi缺陷结构的体弹模量和剪切模量小于TiSi合金。这说明,相对于TiSi合金,缺陷引起合金方向键减弱的同时,由压强引起体积变化所产生的抗力降低。此外,硬质材料杨氏模量较高。计算结果表明,TiSi合金及其VTi和SiTi缺陷结构都表现出硬质材料特性,但缺陷的产生导致晶体硬度下降。
泊松比在-1到0.5范围内常用来估计晶体稳定性。计算结果表明TiSi、VTi和SiTi的泊松比都在此范围内,说明其结构稳定,这与波恩稳定条件判断结果一致。泊松比越大,材料塑性越好。从表3中可以看出,相对于TiSi合金完美结构,具有低泊松比的缺陷结构的韧性较低,缺陷降低了TiSi合金的塑性。
根据Pugh假定[17],体弹模量和剪切模量的比值/是另一种预测多晶相脆性和延展性的方法,区分脆性和延展性的标准值为1.75。计算结果表明TiSi合金的/值为2.2822,说明TiSi合金呈现较强延展性。所有缺陷结构的/值都小于1.75,这表明它们都呈现本质上的脆性。这个结果与泊松比讨论结果一致。

表3 TiSi合金及其缺陷结构的弹性系数和泊松比(单位:GPa)
3 结论
采用基于密度泛函理论的第一性原理计算了TiSi合金及其缺陷结构的形成能、形成热和弹性性质。结果表明:
(1) VTi和SiTi缺陷结构的形成能和形成热较小,所以在合金过程中较易产生;
(2) 通过波恩稳定条件和泊松比判别条件分析得到,相对VSi和TiSi缺陷,VTi和SiTi缺陷更稳定,这与形成能和形成热分析结果一致;
(3) 相对TiSi合金,其缺陷结构具有小的体弹模量和剪切模量,这说明缺陷引起合金方向键减弱的同时,由压强引起体积变化所产生的抗力降低;
(4) 泊松比和B/G值分析结果一致表明,相对TiSi合金完美结构,缺陷结构的韧性较低。
[1] 王金友, 葛志明, 周邦彦. 航空用钛合金[M]. 上海: 上海科技出版社, 1985.
[2] Ramos A S, Nunes C A, Coelho G C. On the peritectoid Ti3Si formation in Ti-Si alloys [J]. Mater. Char., 2006, 56 (2):107-111.
[3] Ran H, Niu J, Song B, et al. Microstructure and properties of Ti5Si3-based porous intermetallic compounds fabricated via combustion sunthesis [J]. J. Alloys Com., 2014, 612 (5): 337-342.
[4] Enyashin A N, Ivanovskii A L. Structural, cohesive and electronic properties of Ti5Si3nanotubes [J]. Phys. E, 2009, 41 (7): 1217-1221.
[5] Zou C X, Jing G Y, Yu D P, et al. Mechanical properties of TiSi2nanowires [J]. Physics Letters A, 2009, 373 (23-24): 2065-2070.
[6] Holloway K, Moine P, Delage J, et al. Structure of an amorphous Ti-Si alloy formed by thermal reaction [J]. J. Non-Cryst., 1991, 134 (1-2): 133-140.
[7] Thomans R M, Ann E M. Calculating the vacancy formation energy in metals: Pt, Pd, and Mo.Phys [J]. Rev. B, 2002, 66: 214110.
[8] Segall M D, Lindan P, Probert M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code[J]. J. Phys. Condens Matetter, 2002,14(11): 2717.
[9] Perdew J P, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple [J].Phys. Rev. Lett., 1996, 77: 3865
[10] Fischer T H, Almlof J. General methods for geometry and wave function optimization [J]. J. Phys. Chem. 1992, 96: 9768-9774.
[11] Hammer B, Hansen L B, Norkov J K . Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals [J].Phys. Rev. B, 1999, 59(11): 7413.
[12] 董飞, 何国强, 张贵田. 合金元素Si在钛合金中作用的研究进展[J]. 金属热处理, 2007, 32 (11): 5-10.
[13] Wu M M, Wen L, Tang B Y, et al. First-Principles study of elastic and electronic properties of MgZn2and ScZn2phases in Mg-Sc-Zn alloy [J]. J. Alloys Compd., 2010, 506 (1): 412-417.
[14] Patil S K R, Khare S V, Tuttle B R, et al. Mechanical stability of possible structures of PtN investigated using first-principles calculations [J]. Phys. Rev. B, 2006, 73 (10): 104118.
[15] Born M, Huang K. Dynamical Theory of Crystal Lattices [M], Oxford:, Oxford University Press, 1954.
[16] Yao H Z, Ouyang L Z, Ching W Y. Ab initio calculation of elastic constants of ceramic crystals [J]. J. Am. Ceram. Soc., 2007, 90 (10):3194-3204.
[17] Pugh S F. Relations between theelastic moduli and the plastic properties of polycry stalline puremetal Philos[J]. Mag. Ser., 1954,7 (45): 823-843.
FIRST-PRINCIPLE STUDY ON THE POINT DEFECTIVE STRUCTURES AND MECHANICAL PROPERTY OF B2-TISI ALLOY
SUN Cai-hong, WU Min,*AN Bo
(Department of Physics Weinan Normal University, Weinan, Shanxi 714099, China)
Using a first-principle method base on density function theory, the lattice constant, formation energy, formation enthalpy and elastic properties are calculated for B2-TiSi alloy. The results show that Ti mono-vacancy (VTi) and Si anti-site (SiTi) defect are easier form in the alloy because of their smaller formation energy and formation enthalpy. Alloy defect structures have smaller bulk modulus and share modulus. Comparing to TiSi alloy, defect structures have a lower tenacity.
first-principle; TiSi alloy; point defect
TP317.4
A
10.3969/j.issn.1674-8085.2014.06.016
1674-8085(2014)06-0077-03
2014-08-15;
2014-09-20
国家自然科学基金青年科学基金项目(11304230);渭南师范学院大学生创新项目(13XK072)
孙彩红(1995-),女,陕西宝鸡人,渭南师范学院物理与电气工程学院本科生(E-mail: 565499880@qq.com);
武 敏(1991-),女,陕西蒲城人,渭南师范学院物理与电气工程学院本科生(E-mail: 956187955@qq.com);
*安 博(1981-),男,陕西渭南人,讲师,主要从事材料物理化学研究(E-mail:mranbo@126.com).
