一族亚纯函数的正规定则
2014-10-29张莎莎祖韦华
张莎莎,祖韦华
(湖北大学数学与统计学学院,湖北 武 汉430062)
0 引言
设D是复平面内的一个区域,F是D上的一族亚纯函数.如果对于族F中的任意函数列{fn}都存在一个子列{fnk}在内按球面距离内闭一致收敛于一个亚纯函数或∞,则称F在D内正规[1].
Bloch曾经给出一个猜想,对于亚纯函数值分布的每个Picard型定理,都存在一个正规准则与之对应.尽管总体来看这个原理并不总成立,但是人们仍可以从Picard型定理出发来考虑正规准则.
1959年,Hayman在文献[2]中证明了关于值分布的一个著名结果.
定理A[2]设f是复平面C上的一个亚纯函数,n≥5是一个正整数,a≠0,b是两个有穷复数,若f′-afn≠b,则f是一个常数.
对应于该值分布理论,Hayman在文献[3]中猜想存在相应于定理A的正规准则.
Hayman猜想[3]设n≥3是一个正整数,a≠0,b是两个有穷复数,F是复平面中区域D 上的一族亚纯函数.若对于任意f∈F,f′-afn≠b,则F在D 内正规.
李松鹰[4],李先进[5]分别证明了n≥5时 Hayman猜想是成立的;庞学诚[6]证明了n=4时猜想成立;1995年,陈怀惠等[7]证明了n=3时Hayman猜想也成立,完全解决了Hayman猜想.
定理B[7]设n≥3是一个正整数,a≠0,b是两个有穷复数,F是复平面中区域D 上的一族亚纯函数.若对于任意f∈F,f′-afn≠b,则F在D 内正规.
陈怀惠等[7]给出例子说明了对于亚纯函数族当n=2时Hayman猜想不成立.
随后,陈怀惠[8]证明了当F是全纯函数族时,对于n=2及把导数f′替换为k阶导数f(k)时定理B仍成立.
定理C[8]设n≥2是一个正整数,a≠0,b是两个有穷复数,F是复平面中区域D 上的一族全纯函数.
若对于任意f∈F,f(k)-afn≠b,则F在D 内正规.
对于亚纯函数族,把 Hayman猜想中的导数f′替换为k阶导数f(k)时,庞学诚[6]和Schwick W[9]证明了如下结果:
定理D 设n,k是正整数,n≥k+4,a≠0,b是两个有穷复数,F是复平面中区域D 上的一族亚纯函数.
若对于任意f∈F,f(k)-afn≠b,则F在D 内正规.
陈怀惠等[10]对亚纯函数极点的阶数加上适当的限制条件改进了上面的定理.
定理E 设a≠0,b是两个有穷复数,F是复平面中区域D 上的一族亚纯函数,若对于任意f∈F的极点的阶数至少为l=k+2,f(k)-af3≠b,则F在D 内正规.
最近,徐焱[11]对亚纯函数的极点和零点阶数加上适当限制条件,改进和推广了上述结果,证明了:
定理F是对定理C、D、E的推广和改进.本文中利用连续函数局部度的相关结论,对定理F做了推广,证明了如下结论:
当h(z)≡b,∀z∈D时,定理即为定理F,由此可见,我们的结论极大地推广了已有结论定理F.
1 引理
引理1[12]设F是单内圆上的一族亚纯函数,F中每个函数的零点的重级至少是k,并且
1)若f(z)=0,必有|f(k)(z)|≤A;
2)F在单位圆内不正规,那么对于每一个0≤α≤k,存在
a)实数r,0<r<1;
b)点列zn,|zn|<r;
c)函数列{fn}⊂F;
d)正数列ρn→0+,
在定理的证明中,我们需要下面关于连续函数的局部度的结论:
引理2[13]设M={(φ,U,ω)},其中U是复平面C中的有界开集,φ:→C是连续函数,ω∈C\\φ(∂U),则存在一个从M到整数域Z的函数d:M→Z使得:
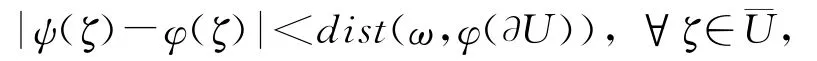
则
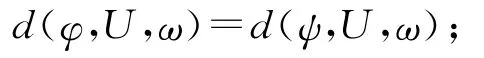
徐焱[11]证明了两个关于值分布理论的结论,我们在证明中也需用到:
将引理3中f(k)-afn≠b替换为f(k)-afn≡b,结论仍成立.
2 定理的证明
定理的证明 反证法,假设F在区域D内不正规.
由正规族的局部性,不妨设F在点z0∈D处不正规.

记

则gj(ξ)在复平面上内闭一致收敛于非常值亚纯函数g(ξ),且由∀f∈F的极点阶数至少为l知g(ξ)极点阶数也至少为l.
由引理3知,必存在ξ0∈C,使得

从而ξ0不是非常值亚纯函数g(ξ)极点.
事实上,若ξ0是g(ξ)极点,设其为l′阶极点,则由(2)式知,k+l′=nl′,从而,即ξ0是g(ξ)的阶数小于l的极点,矛盾.记
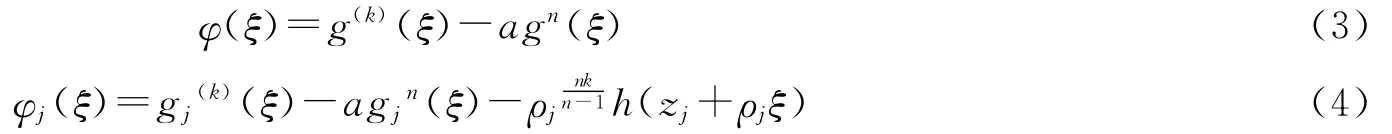
则φj(ξ)在C上内闭一致收敛于φ(ξ).
由ξ0不是g(ξ)的极点知,存在ξ0的某个邻域V,使得φ(ξ)在V 内全纯.φ(ξ0)=0,由全纯函数零点的孤立性知,φ(ξ)在V内的取值只可能是下列的情形1或者情形2.
情形1:若φ(ξ)在V 内只有唯一零点ξ0.
把(1)式代入(4)式可得
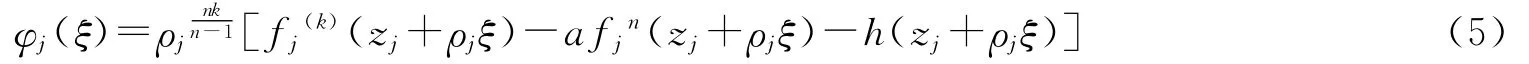
设Δε={ω:|ω|<ε},取ε>0充分小,U 是φ-1(Δε)中包含ξ0的分支中的一个区域,使得
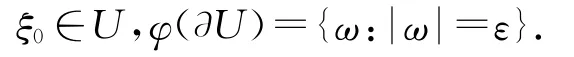
又由于φ(ξ0)=0,故d(φ,U,0)>0,其中,d是连续函数的局部度.
由φj(ξ)在C上内闭一致收敛于φ(ξ)知,当j充分大时有
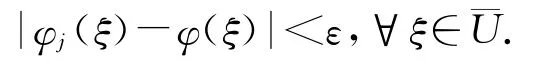
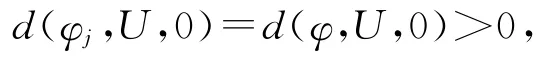
由引理2的(3)知∃ξ1∈U,使得φj(ξ1)=0,由(5)式知
这与定理条件f(k)(z)-afn(z)≠h(z)矛盾.
情形2:若φ(ξ)在V 内恒为0.
由φ(ξ)是亚纯函数知φ(ξ)≡0,即g(k)(ξ)-agn(ξ)≡0,由引理4知g(ξ)≡常数.这与g(ξ)是非常值亚纯函数矛盾.
综上,假设不成立,即F在D内正规.证毕.
[1]Yang L.Value distribution theory[M].Berlin:Spring-Verlag,1993.
[2]Hayman W K.Picard values of meromorphic functions and their derivatives[J].Ann Math,1959,70(1):9-42.
[3]Hayman W K.Research problems in function theory[M].London:Athlone Press,1967.
[4]李松鹰.一类函数的正规定则[J].福建师范大学学报:自然科学版,1984,98:385-393.
[5]李先进.关于正规族的 Hayman猜想的证明[J].中国科学:A辑,1985,28:24-31.
[6]庞学诚.微分多项式的正规定则[J].科学通报,1988,33:1690-1693.
[7]陈怀惠,方明亮.关于fnf′的值分布[J].中国科学:A辑,1995,38:121-127.
[8]Chen H H,Hua X H.Normal families of holomorphic functions[J].J Austral Math Soc Ser A,1995,59:112-117.
[9]Schwick W.Normality criteria for families of meromorphic functions[J].J Analyse Math,1989,52:241-289.
[10]陈怀惠,顾永兴.Marty定则的改进及其应用[J].中国科学:A辑,1993,36(6):674-681.
[11]Yan Xu.Normal families of meromorphic functions[J].J of Math,2001,21(4):381-386.
[12]顾永兴,庞学诚,方明亮.正规族理论及其应用[M].北京:科学出版社:2007.
[13]Pang X C,Zalcman L.Normal families of meromorphic functions with multiple zeros and poles[J].Israel J Math,2003,136(2):1-9.
