关于Lucas数列倒数的无穷和

2014-10-29高丽汪二虎

高丽，汪二虎

（延安大学数学与计算机科学学院，陕西延安716000）

0 引言及主要结论

Fibonacci数列｛Fn｝和Lucas数列｛Ln｝在数论研究和数学应用中具有十分重要的地位，许多作者研究过其性质［1－6］．最近，Ohtsuka H 等［5］研究了 Fibonacci数倒数的求和公式，得出如下结论：

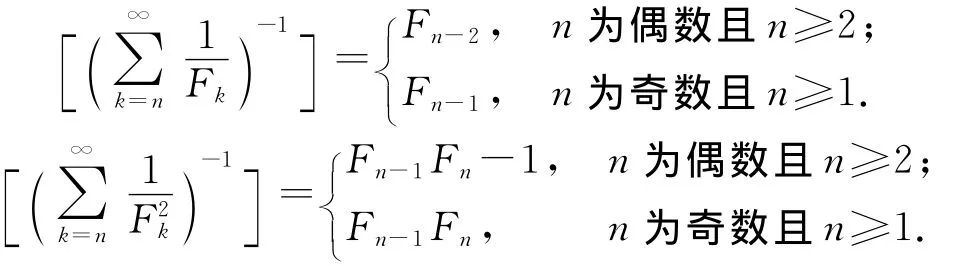
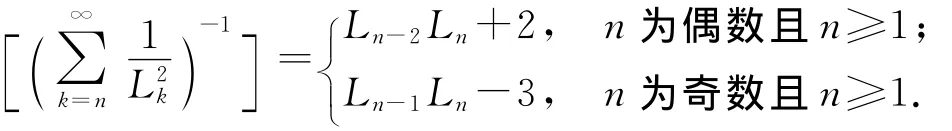
对正整数m，m≥3，是否存在的求和公式仍是一个公开的未解决的问题．

在这一节，我们将直接给出定理的证明．很明显定理和下面不等式是等价的：

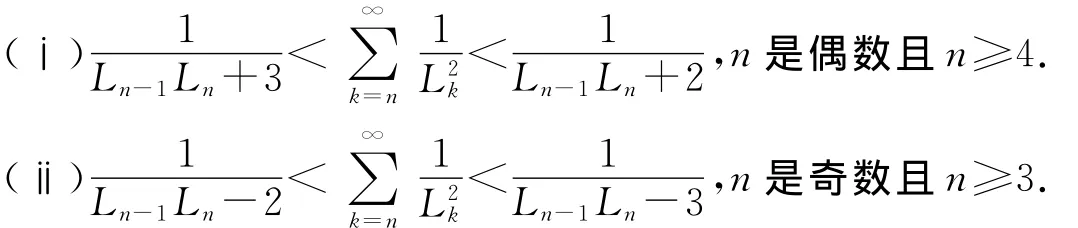
定理的证明首先证明（ⅰ）．如果n是偶数且n≥4，注意到Ln－1＋Ln，利用初等方法我们容易得到：

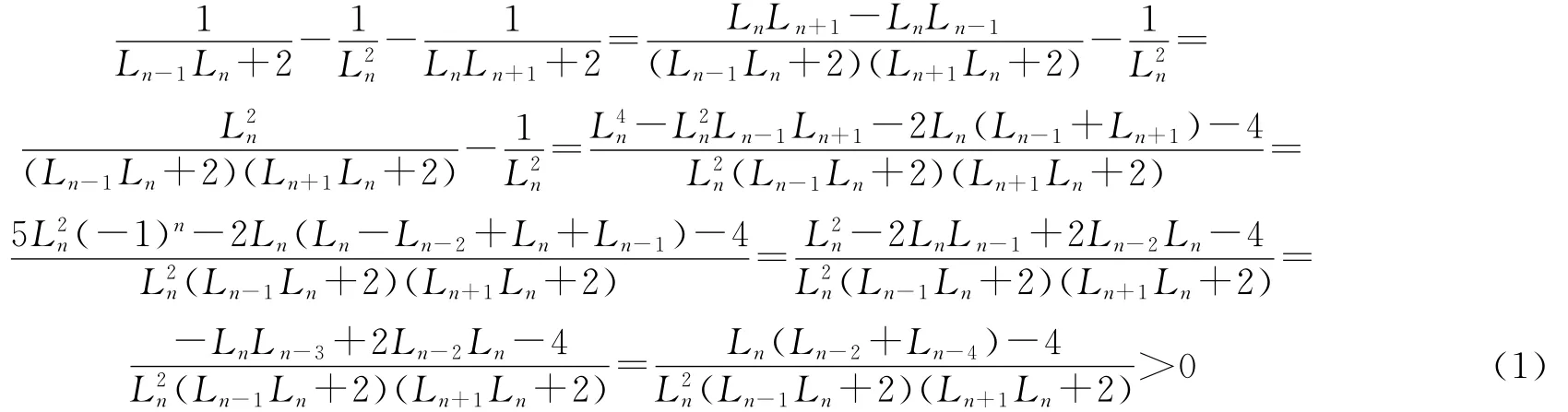
由（1）式可得

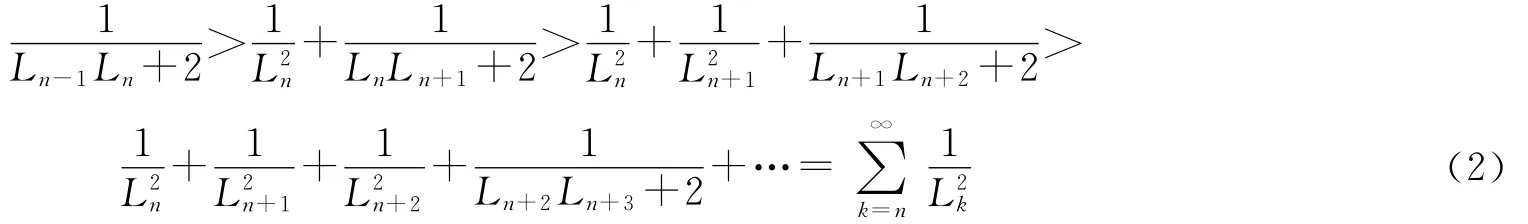
类似地，

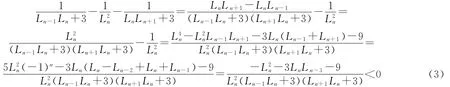
那么

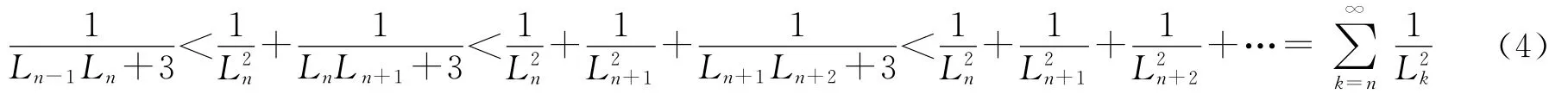
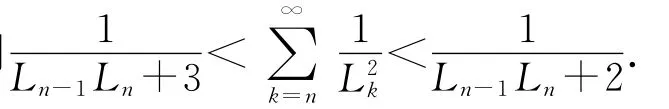
因此由（2）式和（4）式我们可以得到利用同样的方法可证明（ⅱ）．如果n是奇数且n≥3，注意到

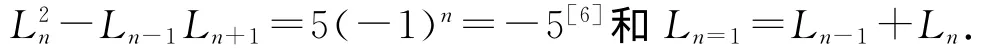
利用初等方法我们很容易得到

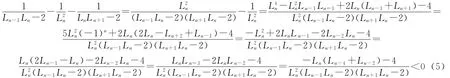
因此

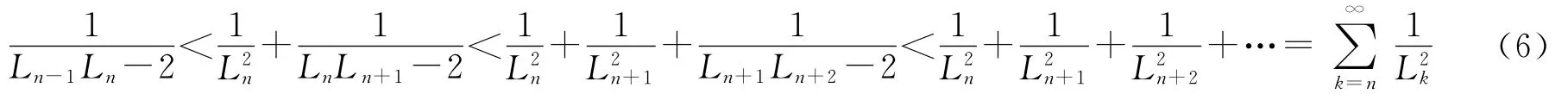
类似地可以得到：

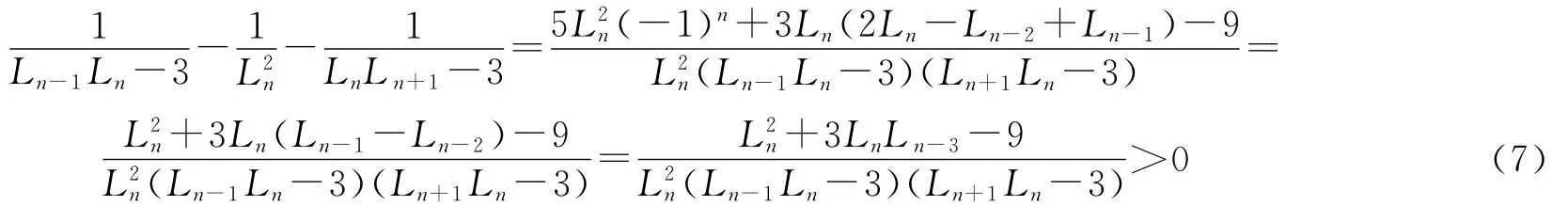
因此

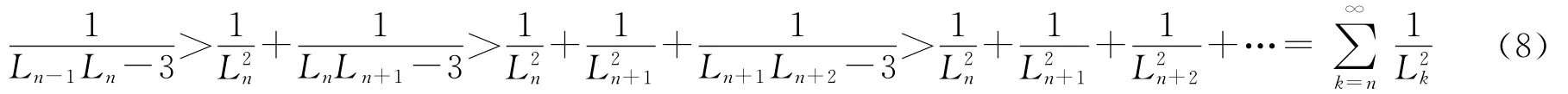
由（6）式和（8）式可得：

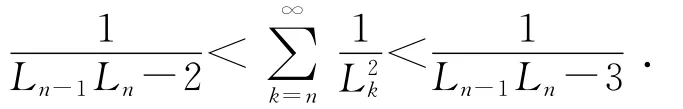
此即完成了定理的证明．

［1］Duncan R L．Applications of uniform distribution to the Fibonacci numbers［J］．The Fibonacci Quarterly，1967，5（2）：137－140．

［2］Wiemann M，Cooper C．Divisibility of an F－Ltype convolution［J］．Applications of Fibonacci Numbers，Kluwer Acad Publ Dordrecht，2004（9）：267－287．

［3］Helmult Prodinger．On a sum of Melham and its variants［J］．The Fibonacci Quarterly，2009，47（3）：207－215．

［4］Ma Rong，Zhang Wenpeng．Severl identities involving the Fibonacci numbers and Lucas numbers［J］．The Fibonacci Quarterly，2007，45：164－170．

［5］Ohtsuka H，Nakamura S．On the sum of reciprocal Fibonacci numbers［J］．The Fibonacci Quarterly，2009，47（2）：153－159．

［6］Zou Xiaowei．A few properties of the Lucas number sequence［J］．Journal of Huanggang Normal University，2006，26（3）：14－15．