焊缝漏磁图像边缘检测算法的实现

崔 巍，赵鹏霄

（1.东北石油大学 机械科学与工程学院，大庆 163318；2.大庆油田有限责任公司第九采油厂，大庆 163853）

在现代制造领域中，焊接是仅次于装配和机械加工的第三大程序，压力容器和化工机械等焊接接头设备在制造和使用过程中易有缺陷产生，通常焊接缺陷易出现在焊缝上及其热影响区内，这些区域一般都具有几何上的不连续性和力学性能上的不均匀性，并且通常是结构中拉伸残余应力最大的地方。常见的焊缝缺陷主要有裂纹、气孔等，其中裂纹是影响焊缝力学性能的主要缺陷。在众多焊接结构的失效事故中，少数一部分是由于选材不当、设计不合理以及操作上的问题引起的，大多数是由焊接裂纹引起的。由于焊接结构对裂纹较为敏感，裂纹不仅削弱有效承载面积，而且局部裂纹一旦发生，易扩展到整体而形成穿透性缺陷，还可能导致结构的脆断，甚至导致事故。因而采用先进的无损检测技术对焊缝进行检测非常必要。目前国内外常采用射线、超声、磁记忆［1－5］等方法检测焊缝缺陷，笔者借助漏磁检测技术对铁磁性材料的焊接结构中裂纹缺陷较为灵敏的优势，在文献中采用焊缝非接触漏磁检测系统进行试验分析和将采集漏磁信号转换成灰度图的基础上［6－7］，以一定尺寸矩形槽缺陷模拟裂纹缺陷，采用经典边缘检测算子对焊缝不同区域分布矩形槽缺陷进行边缘提取，结合试验结果论述了几种经典算子的不适用性，说明寻找新算法对焊缝漏磁图像进行边缘检测的重要性，进而提出一种基于数学形态学的焊缝漏磁图像边缘提取方法，为焊缝漏磁图像提取提供了新的思路。

图1 现场实际检测缺陷

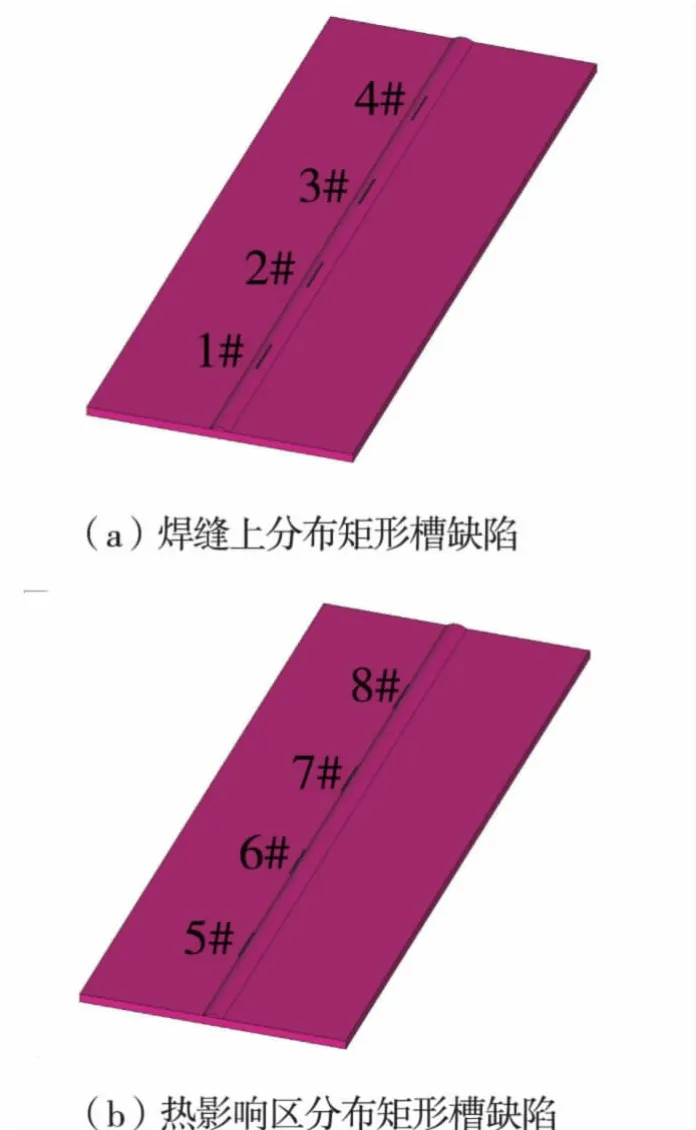
图2 焊缝试验板示意图

1 焊缝矩形槽缺陷漏磁信号的采集

为了分析对接焊缝不同区域（焊缝和热影响区）矩形槽缺陷的分布特征，且由于焊缝及钢板的使用寿命直接与矩形槽缺陷深度有关，因而从缺陷单一深度方向的几何尺寸变化（其他方向的尺寸不变）来分析矩形槽缺陷漏磁图像特征的变化，在长度为1500mm、宽度为400mm、厚度为8mm的焊缝熔宽18mm、余高3mm的Q235试验焊接板上预制了不同深度矩形槽缺陷，分布示意图如图2所示。1＃～8＃矩形槽缺陷的长度均为40mm，宽度均为1mm，深度依次分别为4.6，6.2，7.8，9.4，1.6，3.2，4.8，6.4mm。为保证相邻预制矩形槽缺陷之间相互不受影响，相邻缺陷的中心间隔为140mm。利用磁化方向与行进方向垂直的新型焊缝漏磁检测系统，如图3所示，该系统基于焊缝漏磁检测原理［8］，由磁化结构、信号采集装置、驱动结构等组成，采集的三维漏磁信号如图4所示。

图3 焊缝缺陷非接触漏磁检测系统

图4 焊缝分布矩形槽三维漏磁信号

2 基于经典边缘检测算子的焊缝漏磁图像边缘提取

经典的边缘提取方法是考察原始图像的各个像素在某邻域内灰度的变化，这种不连续性可利用边缘邻近一阶或二阶方向导数变化规律来检测图像边缘。常用的边缘检测算子有：Sobel边缘算子、Roberts边缘算子、Laplace边缘算子、Canny边缘算子。灰度图由256个等级的灰度组成，笔者用不同的灰度等级来表示焊缝漏磁信号幅值的大小，漏磁信号转换成灰度图像的实现过程参见文献［7］中的灰度图像表述。图4中2种状态下的三维漏磁信号转换成灰度图分别如图5（a）、（b）所示。以图5中焊缝上分布矩形槽时灰度图、热影响区分布矩形槽时灰度图为对象，对Sobel、Roberts、Laplace、Canny算法进行编程，得到各算法的边缘检测结果图，如图6（a）～（d）、图7（a）～（d）是分别进行了Sobel算子、Roberts算子、Laplace算子、Canny算子的边缘检测结果图。

图5 焊缝上、热影响区分布矩形槽缺陷原始图像

图6 焊缝上分布矩形槽缺陷时4种算子的边缘检测结果

图7 热影响区分布矩形槽缺陷时4种算子的边缘检测结果

从图6、图7中可以看出，Sobel、Canny等边缘检测算子对焊缝不同位置处矩形槽缺陷均不能有效地提取边缘特征，抗干扰性差，不能有效抑制噪声，检测出的边缘伴随着伪边缘，并且边缘的连续性不好，检测后结果很难区分出边缘信息。常规的边缘检测算子对焊缝矩形槽缺陷漏磁信号图像处理有一定的局限性，因而开展基于数学形态学的焊缝图像识别研究十分必要。

3 基于数学形态学的焊缝漏磁图像边缘提取

3.1 基于数学形态学的边缘检测算子

数学形态学边缘检测是选取合适的结构元素，利用腐蚀、膨胀及开、闭运算这四个基本运算或者它们的有效组合来实现。由形态学运算的结果可知：相比原图像，腐蚀缩小了图像的边界，膨胀扩大了图像的边界，图像基本轮廓不发生改变。因而形态学梯度算子常被用于边缘检测［9－10］，定义为以下三种类型。设f为二值图像或灰度图像，B为结构元素，E为图像边缘。

基于灰度膨胀的边缘提取，边缘检测梯度算子E1为：

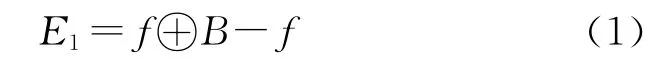
基于灰度腐蚀的边缘提取，边缘检测梯度算子E2为：

基于形态学梯度的边缘提取，边缘检测梯度算子E3为：

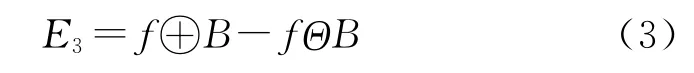
可见，数学形态学边缘检测算子是一种非线性的差分算子，在某种意义上是传统线性差分算子的一种推广。根据焊缝不同位置分布矩形槽时灰度图像特点，对上述灰度图像进行了交互性试验，对比分析上述三种算子对检测准确率的影响，选取检测效果最理想的E1算子。

3.2 结构元素的选取

数学形态学对图像的分析处理主要依据于特定的形态变换，而形态变换的特性由具体的运算和结构元素的几何特征共同决定。结构元素的选取包括结构元素的形状、方向和大小（尺度）。在形状方面，可选取圆盘形、方形、菱形等形状；在方向方面，可选取上、下、左、右、左上、左下、右上和右下等方向；在尺度方面，可选取3×3、5×5、7×7窗口，也可以取更大的尺度。其中，3×3窗口速度快，提取的边缘也比较细腻；圆盘形结构元素对于原点都是对称的，由于各向同性，可以得到与方向无关的运算结果，因此笔者选用3×3圆盘形结构元素，并对比其他类型结构元素，通过交互性试验研究，根据焊缝分布矩形槽缺陷漏磁图像特点，比较几种类型结构元素对检测准确率的影响，最终选用如式（4）所示检测效果最好的3×3的圆盘形结构元素进行边缘检测，即

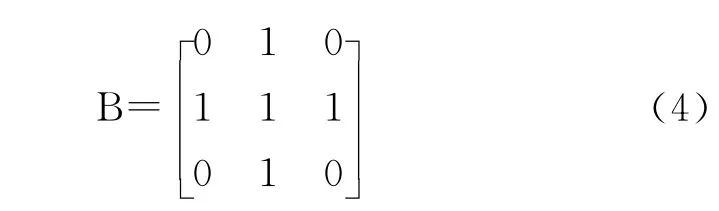
3.3 算法实现及检测结果

笔者首先利用直方图均衡、OTSU法阈值分割对原始图像图5（a）、（b）做预处理，处理结果如图8所示。根据所选用的E1算子，在matlab软件中可通过编程来实现E1算子对图像进行边缘提取，E1算法实现的流程如图9所示，分别对图5（a）、（b）应用式（4）的结构元素、进行E1算子的边缘检测，得到边缘检测结果如图10（a）、（b）所示。

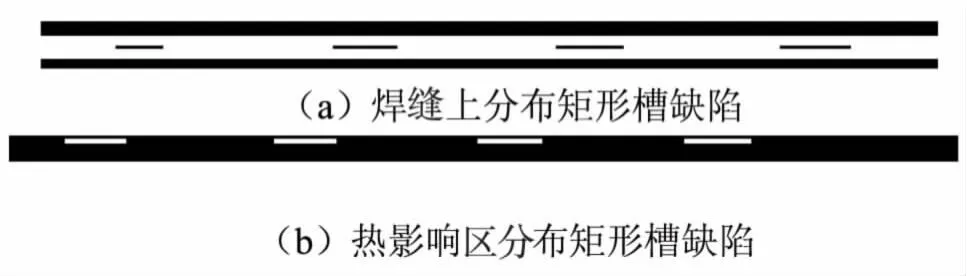
图8 预处理后图像

检测结果表明，基于灰度膨胀的边缘提取算子E1，能有效地检测出焊缝和焊缝不同区域分布矩形槽缺陷的边缘特征，边缘提取的结果实现了二者的分离。根据图像的几何形状及位置：矩形槽缺陷边缘检测图形为窄缝线条，线条顺焊缝延伸的位置与预制矩形槽的位置相对应。检测结果直观可靠，和人的视觉具有良好的一致性。由边缘检测图可直观判断矩形槽在焊缝中分布的位置，结果说明了所提出方法的可行性与有效性。

4 结论

（1）将采集的焊缝不同区域矩形槽缺陷漏磁信号转换成灰度图像的基础上，探讨了经典边缘检测算子Sobel、Roberts、Laplacian、Canny算子对上述漏磁图像的应用效果，检测出的边缘伴随着伪边缘，检测后结果很难区分出边缘信息，说明了上述几种经典算子对焊缝不同区域矩形槽缺陷漏磁图像的不适用性。

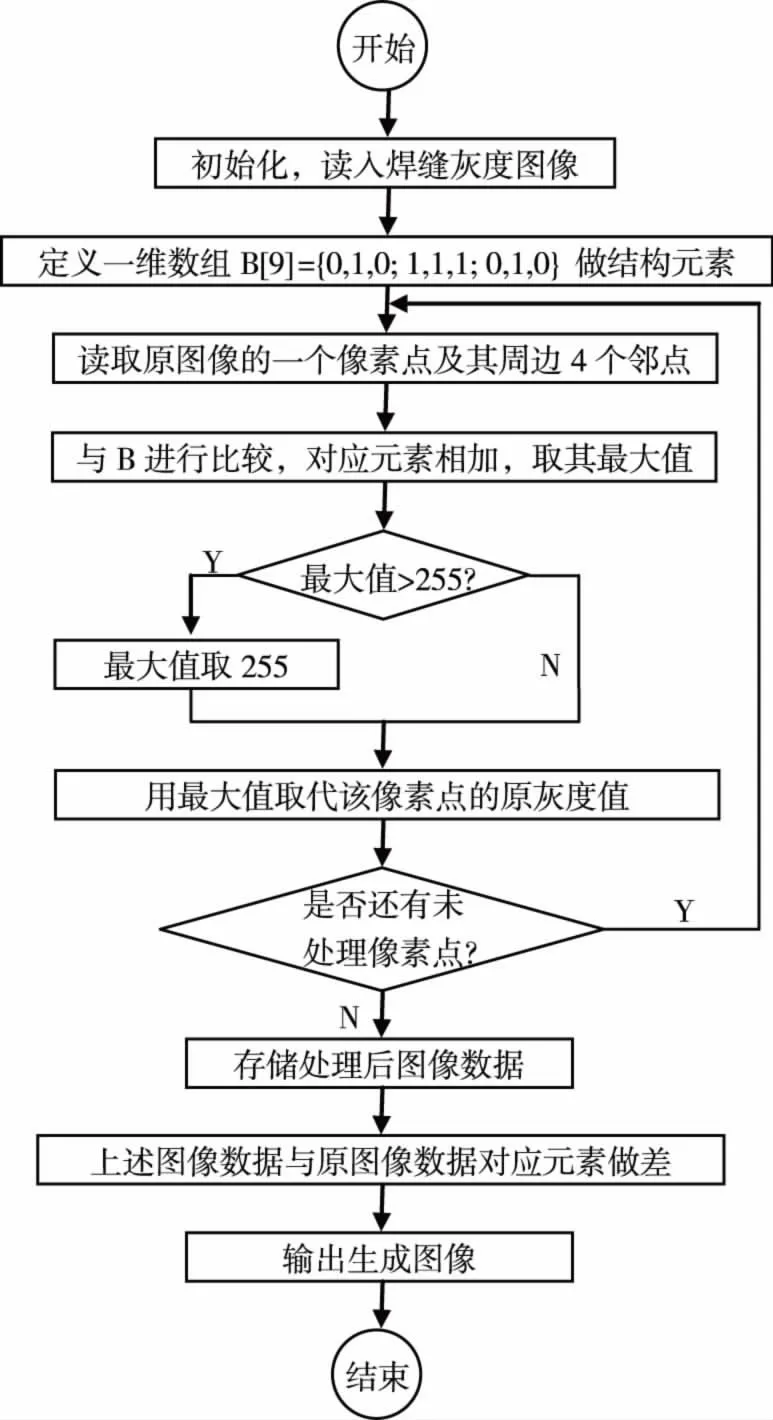
图9 E1算法实现的流程图

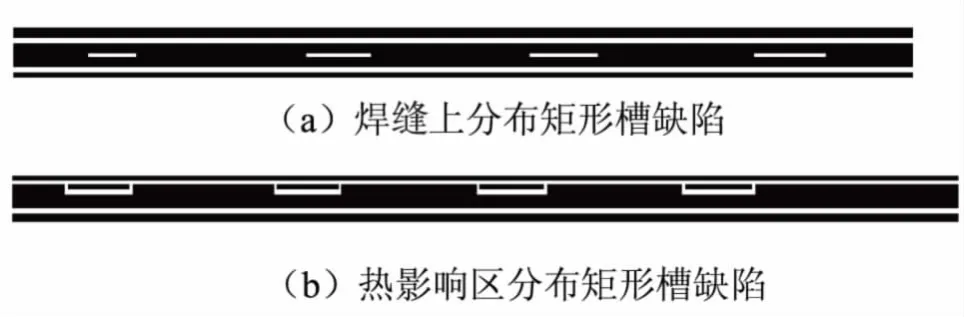
图10 E1算法边缘检测结果

（2）根据焊缝分布矩形槽缺陷漏磁图像特点，将数学形态学方法引入上述图像的边缘检测中。利用形态学边缘检测算子提取焊缝不同区域分布矩形槽缺陷的漏磁信号图像的焊缝缺陷边界，检测结果边缘轮廓清晰，获得了良好的边缘图像特征，实现了上述漏磁图像中焊缝和缺陷二者的有效分离。

［1］DU Dong，CAI Guo－rui，TIAN Yuan，et al.Automatic inspection of weld defects with x－Ray real－time imaging［J］.Lecture Notes in Control and Information Sciences，2007，362：359－366.

［2］SHAO Jia－xin，DU Dong，CHANG Bao－hua.Automatic weld defect detection based on potential defect tracking in real－time radiographic image sequence［J］.NDT＆E International 2012，46：14－21.

［3］CHERTOV A M，KARLOFF A C，PEREZ W.et al.In－process ultrasound NDE of resistance spot welds［J］.Insight－Non－Destructive Testing and Condition Monitoring，2012，54（5）：257－261.

［4］邓 波，郭少宏，曹福想，等.薄板奥氏体不锈钢对接焊缝超声波探伤方法研究［J］.压力容器，2012，29（6）：14－17.

［5］GROSLIER D，PELLERIN S，VALENSI F.Explorative approach of the spectral analysis tools to the detection of welding defects in lap welding［J］.Nondestructive Testing and Evaluation，2011，26（3）：13－18.

［6］崔巍，戴光，王学增.单面焊焊道表面缺陷漏磁检测方法研究［J］.压力容器，2013，30（2）：22－28.

［7］戴光，崔巍，张颖，等.基于灰度－梯度共生矩阵的焊缝缺陷聚类分析［J］.中国安全科学学报，2013，23（3）：79－85.

［8］崔巍，戴光，陈志华，等.基于三维数值模拟的焊缝缺陷漏磁场分析［J］.无损检测，2012，34（8）：10－16.

［9］翟改霞，王春光，张海军.数学形态学梯度算子检测铸铁金相图像边缘［J］.计算机工程与设计，2008，29（4）：1019－1021.

［10］武妍，魏广英，葛菊萍，等.基于形态学双梯度算子的图像边缘检测［J］.计算机工程与应用，2007，43（36）：58－59.