分组密码TWIS的三子集中间相遇攻击

郑雅菲，卫宏儒

(北京科技大学 数理学院，北京 100083)

1 引言

TWIS是由Ojha等人于2009年提出的轻量级分组密码算法[1]，设计思想基于 CLEFIA[2]，采用广义Feistel结构，设计者称其分组长度与密钥长度均为128 bit，加密轮数为10轮。算法的设计文章未给出任何密钥恢复攻击。Su Bozhan等人首先对其进行了安全性分析，通过构造10轮差分区分器，给出全10轮TWIS不抵抗差分分析的结论[3]。随后，Onur Kocak 与Nese Oztop给出了TWIS安全性的进一步研究，差分分析全10轮的TWIS，恢复12 bit末轮轮密钥的计算复杂度为221；构造了9.5轮的不可能差分区分器与线性区分器；指出 TWIS的实际密钥长度仅为62 bit，而不是设计者宣称的128 bit[4]。

中间相遇攻击(meet-in-the-middle attack)由Diffie与Hellman于1977年针对DES的安全性提出[5]。其基本思想为寻找轮数尽可能长的独立密钥，对已知明密文对分别进行加密与解密操作，再选定中间变量进行匹配，筛选正确密钥。中间相遇攻击对算法结构、密钥生成策略有较严格的要求，具有数据复杂度极低的优点。中间相遇攻击目前已应用于DES、AES、Keeloq等分组密码算法的安全性分析中，详细过程与结果可参见文献[6～10]。

基于传统的中间相遇攻击，产生了很多改进后的攻击方法，例如，三子集中间相遇攻击。三子集中间相遇攻击由Andrey Bogdanov等人在轻量级分组密码KTANTAN[11]的安全性分析中首次提出，通过改进密钥子集合的选取与部分匹配技术的应用，增加了传统中间相遇攻击可分析的轮数。将三子集中间相遇攻击应用于全轮KTANTAN32、KTANTAN48，攻击的数据复杂度分别为3/2个明密文对，计算复杂度分别为275.044/275.584[12]。三子集中间相遇攻击有效地拓宽了中间相遇攻击在分组密码安全性分析中的应用。其他应用可参见Gautham Sekar等人对XTEA算法的安全性分析[13]。

本文通过研究分组密码TWIS轮密钥生成的缺陷，对忽略后期白化过程的全10轮TWIS应用三子集中间相遇攻击。恢复实际全部62 bit密钥信息的计算复杂度为245，数据复杂度仅为一个已知明密文对，攻击结果表示TWIS算法不抵抗三子集中间相遇攻击。本文的计算复杂度与数据复杂度均优于TWIS现有的安全性分析结果。

2 分组密码TWIS介绍

2.1 符号说明

A(l)：A的长度为l bit。

＜＜＜ i：左循环移位i bit。

＞＞＞j：右循环移位j bit。

A⊕B：A和B按比特取异或和。

A∧B：A和B按比特取与。

|A|：集合A中的元素个数。

φi,j：第i轮到第j轮的加密过程。

2.2 分组密码TWIS

TWIS是轻量级分组密码，其分组长度与密钥长度均为128 bit，算法结构为2-分支的广义Feistel结构，迭代轮数为10，每轮的轮密钥长度为32 bit。令 P(128)=(P0,P1,P2,P3)表示128 bit明文输入，C(128)=(C0,C1,C2,C3)表示128 bit密文输出，RKi(i=0,1,…,10)表示轮密钥，则TWIS的加密过程如下

其中，轮函数G的输入为3个32 bit的分组，包括2个32 bit分支及一个32 bit轮密钥，输出为2个32 bit的分组。

F函数实现算法的密钥混合，本文攻击不涉及其具体计算，故不进行详细介绍，可参见文献[1]。

TWIS算法通过密钥生成策略由128 bit的初始密钥K得到11个32 bit的轮密钥 RKi(i=0,1,…,10)，其中RK0与RK1为初始白化密钥，RK2与RK3为最后的白化密钥。

各轮轮密钥的具体生成过程为

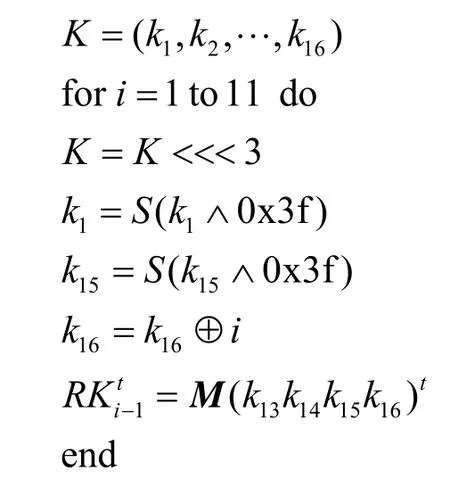
其中，S与F函数中用到的S盒相同，M为混淆矩阵。

3 三子集中间相遇攻击简介

三子集中间相遇攻击是中间相遇攻击的一种改进方法，通过放宽选取密钥子集合的严格要求，使得攻击的应用范围变广。与传统中间相遇攻击将密钥空间划分为2个完全独立的子密钥集合不同，三子集中间相遇攻击将密钥空间划分为3个子密钥集合。

如图1所示，令l为密钥长度，K=k0k1…kl-1表示初始密钥。定义K1={ki|应用于φ1,α的密钥比特集合}，K2={ki:应用于 φR-β+1,R的密钥比特集合}，A0=K1∩ K2表示加密过程φ1，α与 φR-β+1,R的共用密钥集合，则A1=K1K1∩K2与A2=K2K1∩ K2表示仅在φ1,α与 φR-β+1,R中使用的密钥集合，并有 K=K1∪K2。

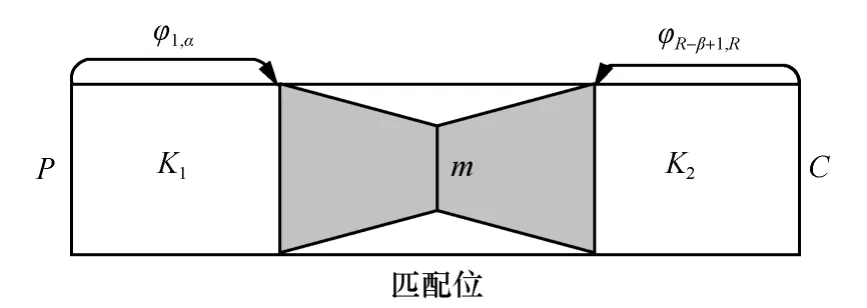
图1 三子集中间相遇结构

当R-β+1=α时，三子集中间相遇攻击等价于中间相遇攻击。

三子集中间相遇攻击的过程包括2个步骤：首先建立三子集中间相遇结构，并利用该结构过滤部分错误密钥，减小密钥空间；然后通过进一步的密钥筛选寻找正确密钥。

首先建立三子集中间相遇结构。

1)猜测A1中密钥的所有可能值，计算v=φ1，α(P)；

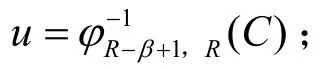
3)确定进行中间匹配的轮数，对v与u分别进行加密与解密运算，得到匹配轮数处对应的加密结果v’与解密结果u’的m(1≤m≤b)个比特，并对m个比特值进行匹配，若m个比特值不完全相同，则认为是错误密钥。该步对密钥的筛选概率为2-m，即经过该步筛选后剩余密钥数为2l-m。

该步的计算复杂度为

接下来，进一步对剩余所有密钥进行筛选。

穷举搜索剩余的所有密钥候选值，利用明密文对(P,C)计算中间匹配轮数处v’与u’的值，并对其全部b比特值进行匹配，若b比特值不完全相同，则认为是错误密钥。一次匹配可删除2b个错误密钥。对剩余的2l-m-b个可能密钥候选值重复该过程，直到得出唯一的正确密钥。

该步的计算复杂度为

罗译：...since he is almost of the same age and as erudite as another man...[6]64

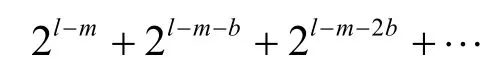
综上所述，完整三子集中间相遇攻击的计算复杂度可表示为

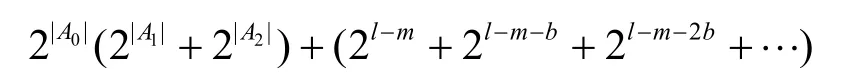
在对密钥子集合的划分中，只要|A1|+|A2|＞2，即可得到优于穷举搜索的计算复杂度。

4 TWIS的三子集中间相遇攻击

TWIS算法的设计者称其密钥长度为128 bit，但是观察其密钥生成策略可以发现，每轮变换循环移位仅3 bit，值改变的量仅为24 bit。这使得初始密钥的混淆速度非常慢。经过推导可发现其实际密钥长度仅为62 bit，且忽略后期白化后，算法首尾两端可找到较长轮数的独立密钥。

本文攻击利用该特点，通过推测各轮的轮密钥，对忽略后期白化过程的全10轮TWIS应用三子集中间相遇攻击。

表1 TWIS各轮轮密钥

4.1 轮密钥推导

三子集中间相遇攻击利用TWIS一些密钥比特在连续的多轮加密过程中未被使用的特点。所以为了建立TWIS的三子集中间相遇结构，首先推导各轮加密使用的轮密钥。根据TWIS密钥生成策略得到的各轮轮密钥的使用情况如表1所示。

观察各轮轮密钥的使用情况可以发现，虽然TWIS的设计者称其密钥长度为128 bit，但实际有效的密钥长度仅为62 bit，即在轮密钥生成过程中，仅使用了初始密钥的{k0,k1,…,k32,k99,k100,…,k127}这62 bit，而其他66 bit无效。这使得对TWIS的穷举搜索复杂度由 2128降为262。记实际密钥空间为K′={k0,k1,…,k32,k99,k100,…,k127}。

4.2 10轮TWIS的三子集中间相遇攻击

在TWIS实际密钥长度l=62的基础上应用三子集中间相遇攻击，使得复杂度进一步降低。

考虑初始白化密钥，忽略后期白化密钥，观察各轮轮密钥可有如下发现。

从第0轮至第4轮的轮密钥涉及的密钥比特集合为{k0,k1,…,k14,k99,k100,…,k127}，未使用实际密钥的18个比特集合为{k15,k16,…,k31,k32}。

从第7轮至第10轮的轮密钥涉及的密钥比特集合为{k0,k1,…,k32,k117,k118,…,k127}，未使用实际密钥的18比特集合为{k99,k100,…,k115,k116}。

利用TWIS轮密钥的上述2个重要特点，根据第 3节中对三子集中间相遇攻击思想与过程的介绍，选取α=4，β=7，即可将实际密钥空间划分为3个子集合A0、A1和A2，划分方式如下

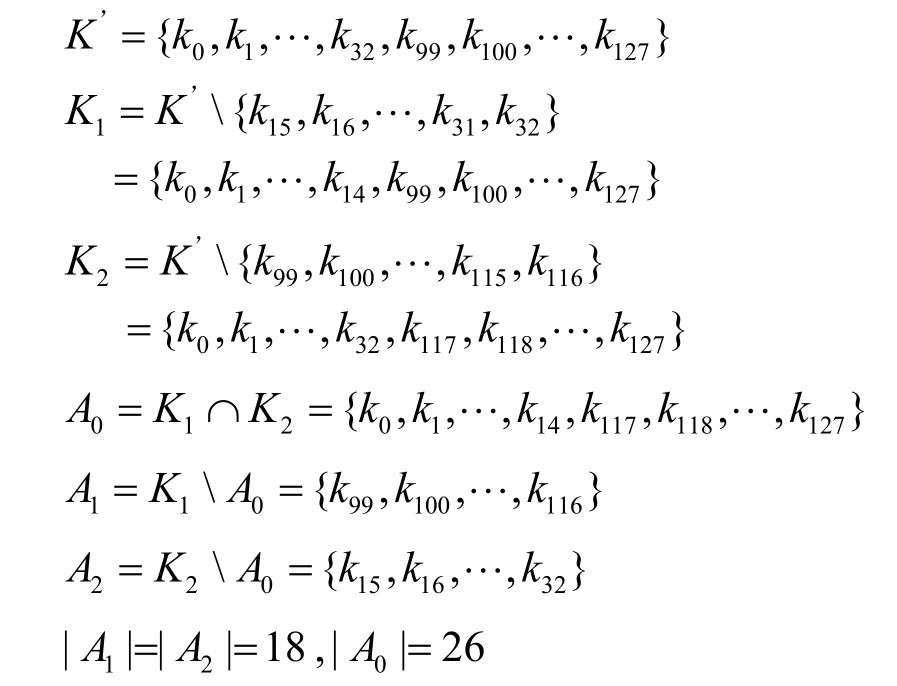
利用这些参数即可得到10轮TWIS的三子集中间相遇结构，并对密钥进行初步筛选。具体过程如下。

已知一个明密文对(P,C)，对A0的 226种可能值。

1)猜测A1中密钥的所有 218种可能值，计算v=φ1,4(P)。

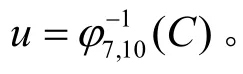
3)选择第5轮为中间匹配轮数，得到第5轮处的v’与u’，具体推导过程如图2所示。图中黑色部分表示受独立密钥A1、A2影响，白色部分表示不受影响。对v’与u’均不受独立密钥影响的32个比特值进行匹配，若 32个比特值不完全相同，则认为是错误密钥，筛选概率为2-32。

该步的计算复杂度为：226(218+218)=245。

图2 中间匹配过程

接下来，穷举搜索剩余 2l-m=230个密钥候选值，利用明密文对(P,C)重新计算v’与u’的值，并对其128 bit值进行匹配，若128 bit值不完全相同，则认为是错误密钥，该步的筛选概率为2-128。重复该步骤，直到得到满足v’=u’的唯一正确密钥。

该步的计算复杂度为

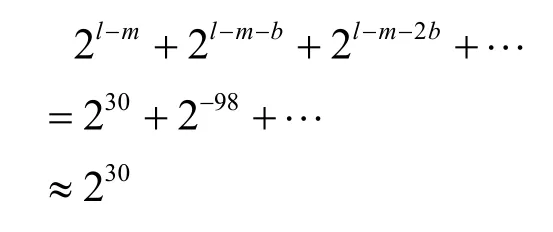
观察上式可发现，对TWIS只需要一步筛选即可期待淘汰所有错误密钥，得到唯一的正确密钥。

4.3 复杂度分析

根据第3节中对三子集中间相遇攻击复杂度计算的介绍，恢复10轮TWIS实际全部62 bit密钥信息的计算复杂度为

5 结束语

如表2所示，针对TWIS算法密钥生成策略中存在的缺陷，本文首次对忽略后期白化的全10轮TWIS应用了三子集中间相遇攻击。恢复实际密钥的全部62 bit密钥信息的数据复杂度仅为一个明密文对，计算复杂度为245，分析结果表明忽略后期白化的全10轮TWIS算法不抵抗三子集中间相遇攻击。本文结果优于文献[4]中Onur Kocak等人差分攻击10轮TWIS得到的结果。

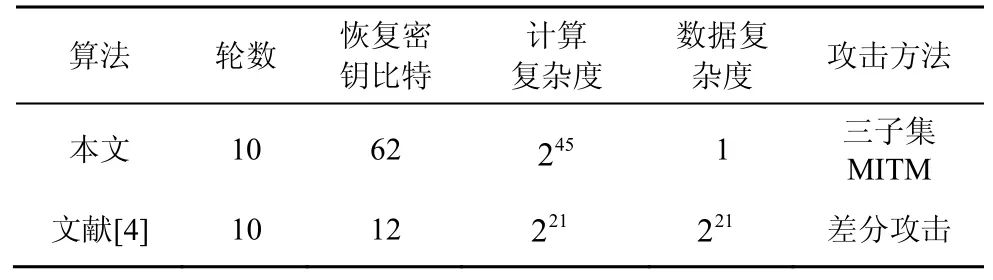
表2 TWIS安全性分析结果

[1]OJHA S K,KUMAR N,JAIN K. TWIS–a lightweight block cipher[A].Information Systems Security[C]. Berlin: Springer Heidelberg,2009.280-291.

[2]SHIRAI T,SHIBUTANI K,AKISHITA T,et al. The 128 bit block cipher CLEFIA[A]. Fast Software Encryption[C]. Berlin: Springer Heidelberg,2007.181-195.

[3]SU B Z,WU W L,ZHANG L,et al. Full-round differential attack on TWIS block cipher[A]. Information Security Applications[C]. Berlin:Springer Heidelberg,2011.234-242.

[4]KOCAK O,OZTOP N. Cryptanalysis of TWIS block cipher[A]. Research in Cryptology[C]. Berlin: Springer Heidelberg,2012.109-121.

[5]DIFFIE W,HELLMAN M E. Special feature exhaustive cryptanalysis of the NBS data encryption standard[J]. Computer,1977,10(6): 74-84.

[6]CHAUM D,EVERTSE J H. Cryptanalysis of DES with a reduced number of rounds[A]. Cryptology-CRYPTO’85 Proceedings[C]. Berlin: Springer Heidelberg,1986.192-211.

[7]DEMIRCI H,SELCUK A A. A meet-in-the-middle attack on 8-round AES[A]. Fast Software Encryption[C]. Berlin: Springer Heidelberg,2008.116-126.

[8]DEMIRCI H,TASKM İ,COBAN M,et al. Improved meet-in-themiddle attacks on AES[A]. Progress in Cryptology- INDOCRYPT 2009[C]. Berlin: Springer Heidelberg,2009.144-156.

[9]DUNKELMAN O,SEKAR G,PRENEEL B. Improved meet-in-themiddle attacks on reduced-round DES[A]. Progress in Cryptology–INDOCRYPT 2007[C]. Berlin: Springer Heidelberg,2007.86-100.

[10]INDESTEEGE S,KELLER N,DUNKELMAN O,et al. A practical attack on keeloq[A]. Cryptology-EUROCRYPT 2008[C]. Berlin: Springer Heidelberg,2008.1-18.

[11]DE C C,DUNKELMAN O,KNEZEVIC M. KATAN and KTANTAN—a family of small and efficient hardware-oriented block ciphers[A]. Cryptographic Hardware and Embedded Systems-CHES 2009[C]. Berlin: Springer Heidelberg,2009.272-288.

[12]BOGDANOV A,RECHBERGER C. A 3-subset meet-in-the-middle attack: cryptanalysis of the lightweight block cipher KTANTAN[A].Selected Areas in Cryptography[C]. Berlin: Springer Heidelberg,2011.229-240.

[13]SEKAR G,MOUHA N,VELICHKOV V,et al. Meet-in-the-middle attacks on reduced-round XTEA[A]. Topics in Cryptology–CT-RSA 2011[C]. Berlin: Springer Heidelberg,2011.250-267.