复合衰落信道下分布式MIMO系统下行中断概率分析

彭文杰，李岳衡，居美艳，黄平，谭国平

(河海大学 计算机与信息学院，江苏 南京 211100)

1 引言

多输入多输出（MIMO）技术能在不增加系统带宽的情况下成倍提高MIMO系统容量，且信道可靠性亦大为增强[1]。分布式天线系统（DAS）作为传统MIMO技术的拓展，通过将天线在小区内分开放置以提高接收信噪比，进而提高整个系统的无线信号覆盖能力[2]。由于分布式MIMO系统综合了传统MIMO和分布式天线系统的优点，其各对收发链路之间将更加独立，故具有大容量、低功耗、更好的信号覆盖等优势[4～6]，因而被认为是未来B4G/5G无线通信系统的备选方案之一。

不过在分布式MIMO系统投入实际应用前，包括诸如分布式天线端口在小区内位置最优配置以及各天线发射功率分配在内的系统上层网络规划将是设计者所面临的一个关键问题。而系统中断概率作为衡量无线通信系统整体性能的一项重要指标，其参数值能非常有效地指导MIMO系统网络规划，因此研究系统中断概率显然具有极其重要的理论指导及应用价值。

文献[7]则综合考虑了Rayleigh衰落、阴影衰落和路径损耗，建立了一个复合衰落信道模型，并推导出中断概率的显性表达式，但路径损耗被设定为固定值，这与实际情况明显不符。文献[9]完善了文献[8]中的系统模型，综合考虑了Nakagami-m衰落、阴影衰落和路径损耗，推导得到了分布式MIMO系统的系统中断概率。虽然文献[7～9]已比较系统地分析了分布式MIMO系统的中断概率问题，但其分析仍然存在局限性，即所有分析都是基于小区内某一固定位置上的系统中断概率加以分析。文献[10]则进一步考虑了移动台在小区内的分布情况，对比了移动台均匀分布和存在小区热点时的小区平均中断概率，但该文中的移动台分布模型并不能完全客观地反映小区移动台的实际分布情形，故仍有待完善；此外在复合信道建模过程中，其小尺度衰落仅采用简单Rayleigh衰落，这一点也不能体现城市衰落的客观实际。

本文将在前人研究成果的基础之上对上述论文中有关分布式 MIMO系统中断概率研究中的不完善之处进行改进。首先综合考虑Nakagami-m衰落、路径损耗和阴影衰落，建立较完善的Gamma-Lognormal复合衰落信道模型，并搭建一个简单的分布式MIMO系统。然后针对存在中心基站的系统模型，提出一种新的更接近实际应用环境的准均匀小区移动台分布模型，并给出相应概率密度函数。接着利用矩生成函数、Gauss-Hermite积分公式、Simpson积分公式等数学手段推导任意移动台分布下、单小区内系统下行平均中断概率的闭合表达式。最后，将本文提出的准均匀小区移动台分布模型应用到该中断概率闭合表达式中，并通过MATLAB数值仿真验证所推导得到的闭合表达式及小区移动台分布模型的合理性。

2 系统模型

经典分布式MIMO系统结构框如图1所示：假设一个半径为R的圆形小区内，存在Mt个基站，放置在不同位置上，记作BSi，i=1,2,…,Mt。为充分利用空间复用或分集，每个基站上带有L根天线。在本文分析的系统中，存在中心基站BS1，其余分布式基站天线则均匀分布在半径为Rbs的圆上，所有基站天线通过光纤连接到中心处理器[11]。小区内存在移动台 MS，不失一般性地，假设每个移动台带有Mr根接收天线，组成一个简单的分布式MIMO系统。由于是圆形小区，所以采用极坐标，并以小区中心为坐标原点，故BSi位置记作(Rbs,θi)，MS所在位置记作(ρ,θ)。

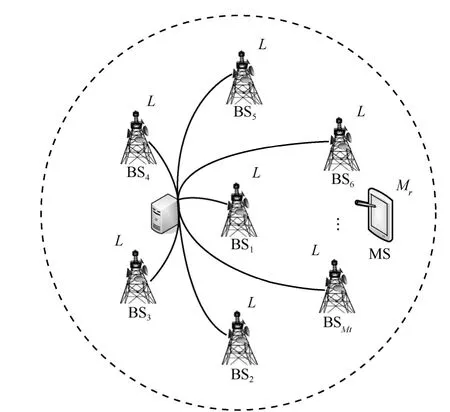
图1 分布式MIMO系统示意

在系统下行传输过程中，基站采用选择—最大比发送机制，即选择能够使移动台接收信噪比最大的基站与之建立链路并进行数据传输，而基站内多天线则采用最大比发送。为简化问题的分析，本文在采用选择发送机制时仅考虑接收信噪比而不是信干噪比作为判决度量，这是因为在实际应用中，为了克服多用户通信时存在的同频干扰，系统一般都会引入导频信道以供测量之需；而导频信道与专用数据传输信道之间可通过采用码分或者时分模式加以区分，如此则可依靠导频信道进行接入基站端口的选择测量而忽略同频干扰。

MS上第 j根天线接收到基站BSi发送的下行信号可以表示为

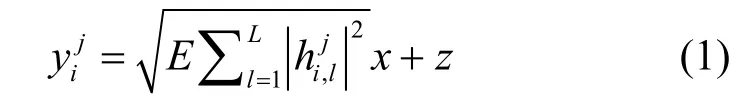
综合考虑包含Nakagami-m衰落、阴影衰落和路劲损耗的复合信道模型，其数学表示为[9]

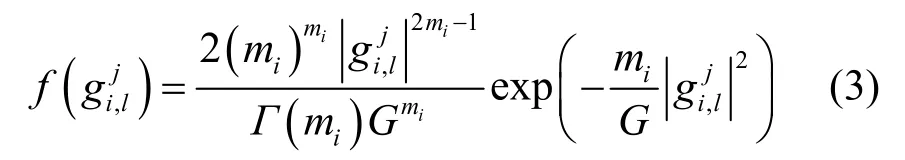
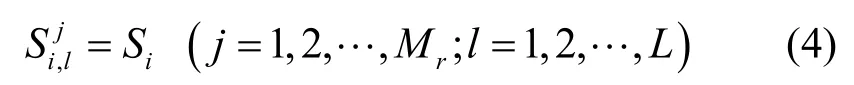
Si服从对数正态分布，概率密度函数为[12]

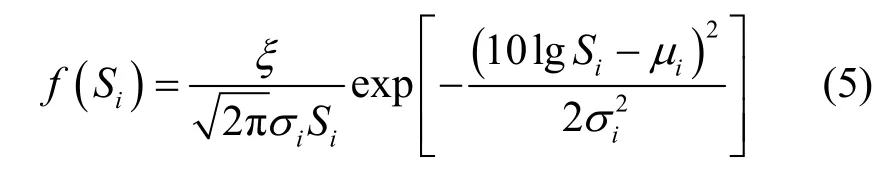
其中，ξ=10 ln10，μi和σi都以dB为单位，分别是10lgSi的均值和标准差。根据文献[13]的研究结果，均值μi与路径损耗有关，可以建模为

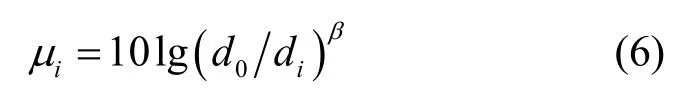
其中，d0为参考距离，β是路径损耗指数，di代表MS与BSi之间的距离，在基站天线位置已知的前提下，与MS所在位置(ρ,θ)有关，可以表示为

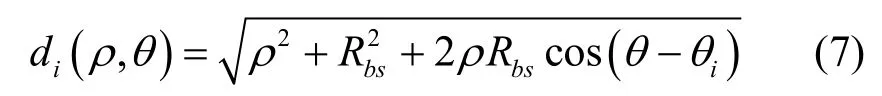
根据上述建模，可以得到MS上第j根接收天线所接收到的信噪比为

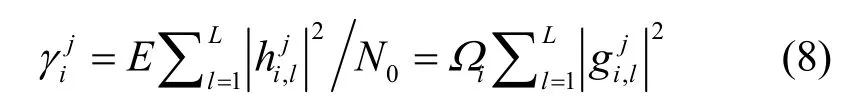
其中，Ωi=ESiN0。由于Si服从对数正态分布，因此Ωi也服从对数正态分布，参照式(5)，其概率密度函数可表示为

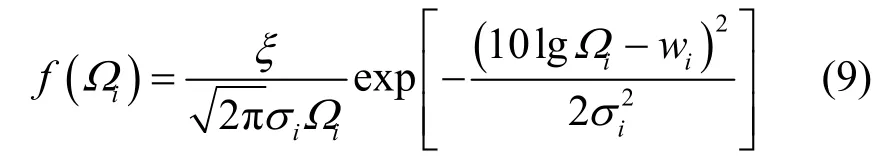
其中，wi=μi+10lg(E N0)，是10lgΩi的均值，标准差仍然为σi。

移动台接受信号时采用最大比合并，得到输出信噪比为

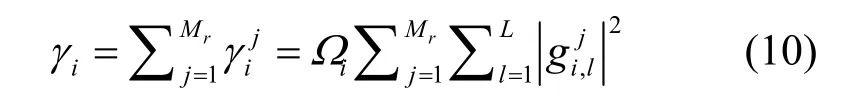
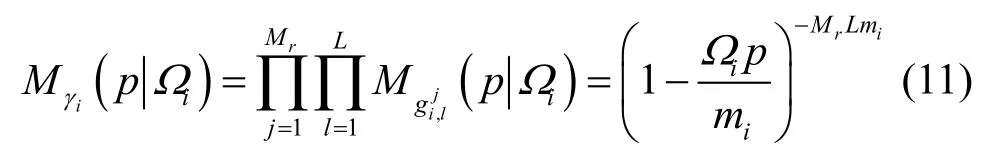
给定Ωi时，γi的条件概率密度函数可以通过对条件矩生成函数先取反，再做拉普拉斯逆变换得到[12]。利用文献[14]中的式(26)，可以得到

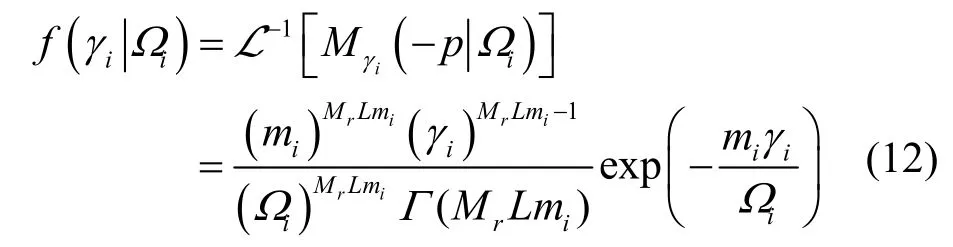
其中，L-1(·)表示拉普拉斯逆变换，Γ(·)为伽马函数。

最后通过对条件Ωi进行概率积分可得输出信噪比γi的概率密度函数为

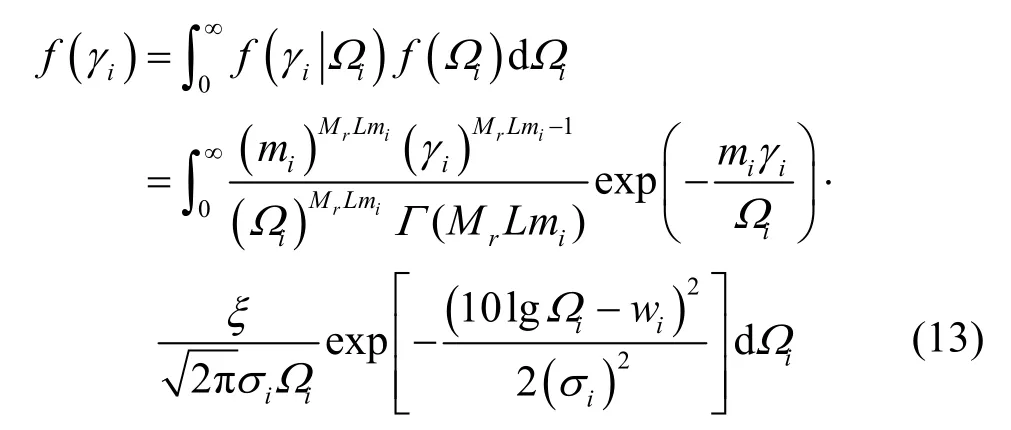
从式(13)可以看出，此时的输出信噪比服从Gamma-Lognormal分布[12]。需要注意，式(13)中wi与移动台在小区内的位置有关，是(ρ,θ)的方程。

3 准均匀小区移动台分布

现有文献对分布式MIMO系统的中断概率等系统性能进行理论分析时，大都将小区内的移动台分布模型建模为均匀分布，即移动台出现在小区内任意位置的概率是相同的；在直角坐标系下，针对本文所研究的圆形小区，其概率密度函数定义为

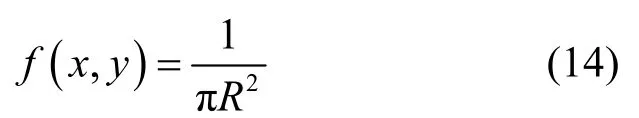
其中，R为圆形小区半径，(x,y)为移动台位置直角坐标。若将移动台位置转换为极坐标(ρ,)θ的形式，取小区中心为原点并假设极距ρ和方位角θ之间相互独立，则根据直角坐标与极坐之间的数学转换，可得二者极坐标形式的概率密度函数分别为[15]

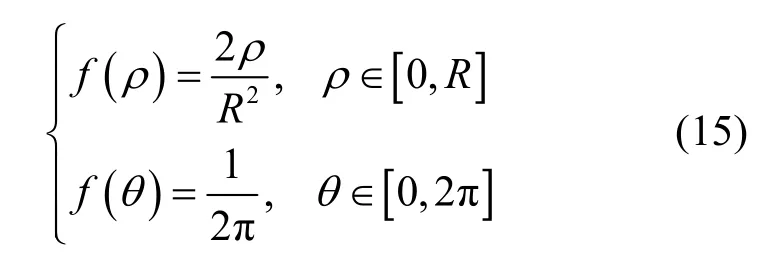
不过在实际应用环境中，小区内的移动台分布往往并不服从均匀分布。在文献[10]中，作者就将圆形小区内移动台位置的分布改进并建模为一种存在热点区域的非均匀分布模型，由于该模型充分考虑了小区内移动台更多地分布于中心区域的这一特征，故较传统均匀分布具有一定的先进性和参考价值。不过该文献因将小区划分为移动台密度不等的2个不同环形区域，而在这2个区域内移动台却分别呈均匀分布，从而形成了一种两级“阶梯状”平台递减分布模型，究其实质只不过是一种变形的均匀分布而已。但在实际环境中，可以预见移动台的分布不会这么简单地分为这样两部分：一般而言，小区中心区域内移动台分布最为密集，距离小区中心越远移动台分布的密度越小；从小区中心到小区边缘，移动台分布的概率密度函数应该连续缓慢递减，而不应该是如文献[10]所述的那样一个二级分段平台函数。

其实如果仔细分析直角均匀分布的极坐标等价式(15)也可以看出该分布的不合理性：所谓的直角均匀分布在方位角θ上服从均匀分布；而在极径ρ上则服从从圆心至小区边缘的单调“递增”分布，显然这与实际基站站点应尽可能放置在用户分布比较密集的区域的这一布设规范相违背。不过受该式启发，本文假设小区内移动台分布服从如图2所示的准均匀分布模型，即在圆形小区内移动台沿极径方向服从“径向线性稀疏”的均匀分布而不是式(15)中的单调递增分布；同时极角的取值仍保持均匀分布不变，此时ρ和θ的极坐标概率密度函数可以分别表示为

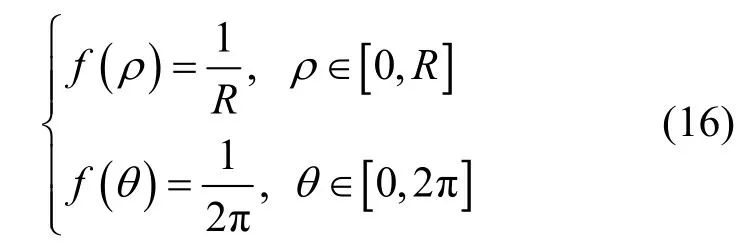
根据与上述推导类似的极坐标到直角坐标的转换，图2所示的小区内移动台位置极坐标均匀分布的等价直角坐标系联合概率密度函数为

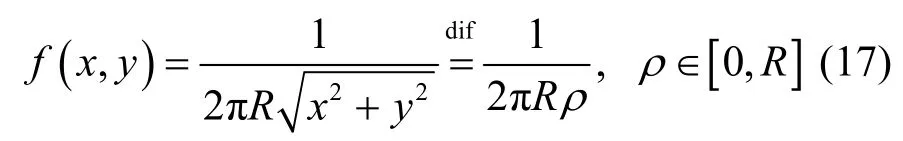
由式(16)可见，虽然移动台的ρ和θ在极坐标下都服从均匀分布，但从直角坐标系的角度来看，其在小区内的分布却已不再是简单的均匀分布，而是沿着极径呈从圆心至小区边缘的一种非均匀平滑线性单调递减特性。

若从小区上层网络规划的角度来分析，基站应该放置于移动台分布密集的地区，或者说移动台应更多地分布在基站周围；而移动台也应自然呈现出一种距基站中心逾远、其分布逾稀疏的态势。基于此小区用户分布的直观特征可以看出：基于传统直角坐标均匀用户分布模型加以极坐标极距密度均匀修正而提出并加以分析的这种新型移动台分布模型是符合实际小区移动台分布预期的，是合理的；相较于传统均匀分布模型以及文献[10]所研究的二级阶梯“平台”递减模型能更好地描述移动台在小区内的分布情况。本文将这种移动台分布模型称为小区移动台“准均匀分布”。

事实上，本文所提出的“准均匀分布”模型的最大特点体现在移动用户直角坐标分布概率密度沿极径线性单调递减的特性上(如式(17)所示)，其数学依据则源于对传统均匀分布等价极坐标公式不合理性的分析与改进；研究该模型的目的也旨在尽可能逼近实际用户分布状况、进而更真实地反映传统分布式MIMO系统的各项性能计算指标。由于小区移动用户分布的真实状况非常复杂，此“准均匀分布”虽不能完全表征系统用户的实际分布情况，但从小区用户沿极径递减的趋势来看，该模型是合理的；该分布模型的提出也可为后续类似的模型研究与进一步改进提供一个新颖的理论参考。

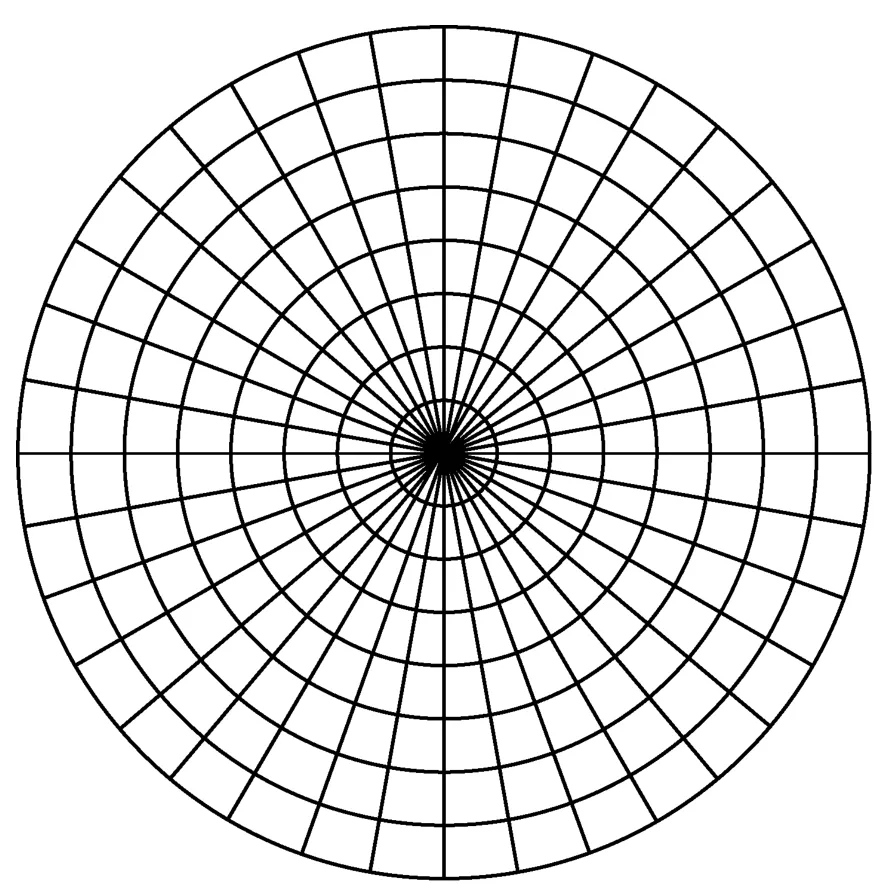
图2 移动台分布示意

4 中断概率分析

在基站天线与移动台之间信道信息已知的前提下，本文采用选择发送机制，即选择能够使移动台接收信噪比最大的基站进行信息发送，因此MSk接收到的信噪比可以建模为

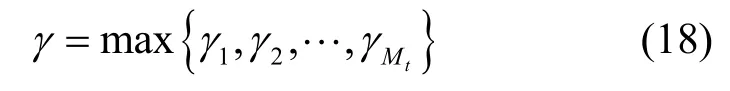
由于各个基站天线之间的距离足够远，对应的接收信噪比γi相互独立，因此系统中断概率可以表示为

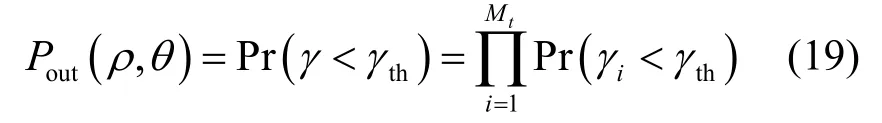
其中，γth是信噪比门限。根据式(13)可以得到Pr(γi＜γth)，但却是一个复杂的积分公式。本文利用 Gauss-Hermite积分公式[15]将复杂的表达式转化为如下简单的闭合表达式

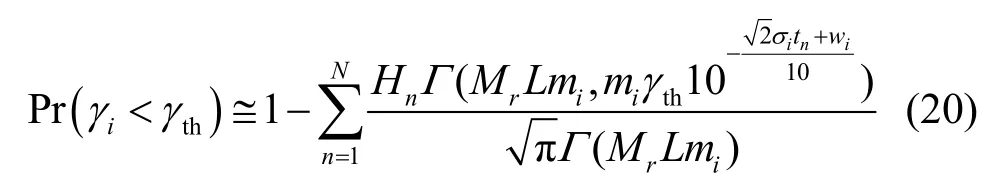
其中，N是Hermite多项式的阶数，tn和Hn分别是N阶Hermite多项式的基点和权重。

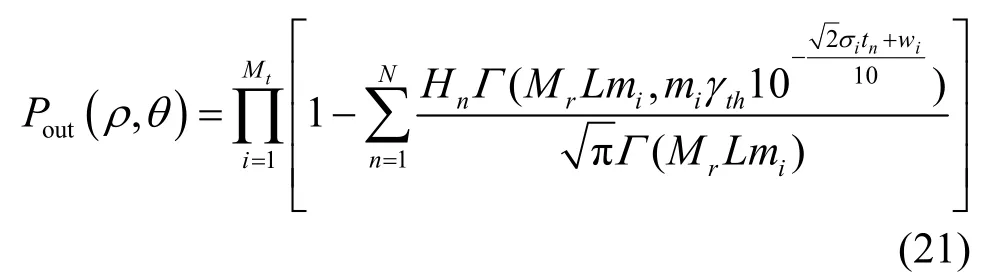
将式(20)代入式(19)，可得系统中断概率为其中，wi是移动台所在位置(),ρ θ的函数，所以该中断概率表达式与移动台在小区内所处位置有关，仅代表处于小区内某一位置点移动台的中断概率值，故不能作为整个系统中断概率分析的指标。为此，考虑移动台在小区内的整体分布情况，得到系统的平均中断概率表达式

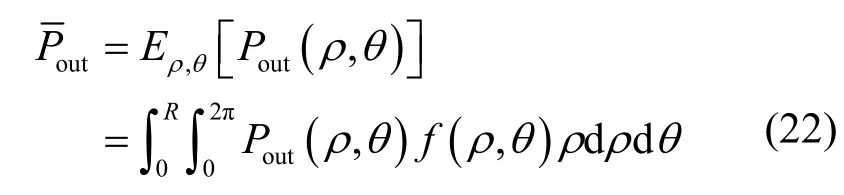
式(22)为非闭合表达式，不利于进一步分析，利用Simpson积分公式[17]将上式进一步简化

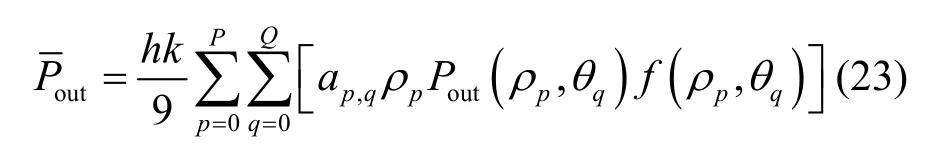
其中，P和Q分别是极径和极角等距划分的节点数，必须为偶数，h=R P，k=2πQ，ρp=ph，θq=qk；ap,q为权值，是权值矩阵A中第p+1行第q+1列元素，而权值矩阵A可以表示为

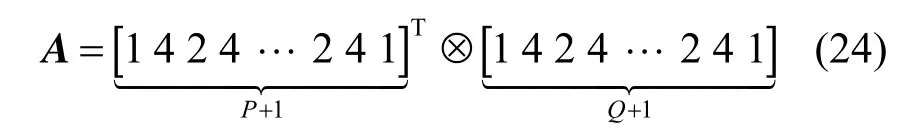
其中，[·]T表示转置，⊗为克罗内克（Kronecker）积。

5 仿真结果与讨论

5.1 仿真及结果

本节将通过 MATLAB软件计算并观测接收天线数目、Nakagami参数、路径损耗指数、小区内移动台分布对系统平均中断概率的影响，以及通过对比理论值和Monte-Carlo仿真值，验证本文推导得到的理论表达式的准确性。系统仿真的主要参数如表 1所示（未加特别标注的皆以表中基本参数为准）。

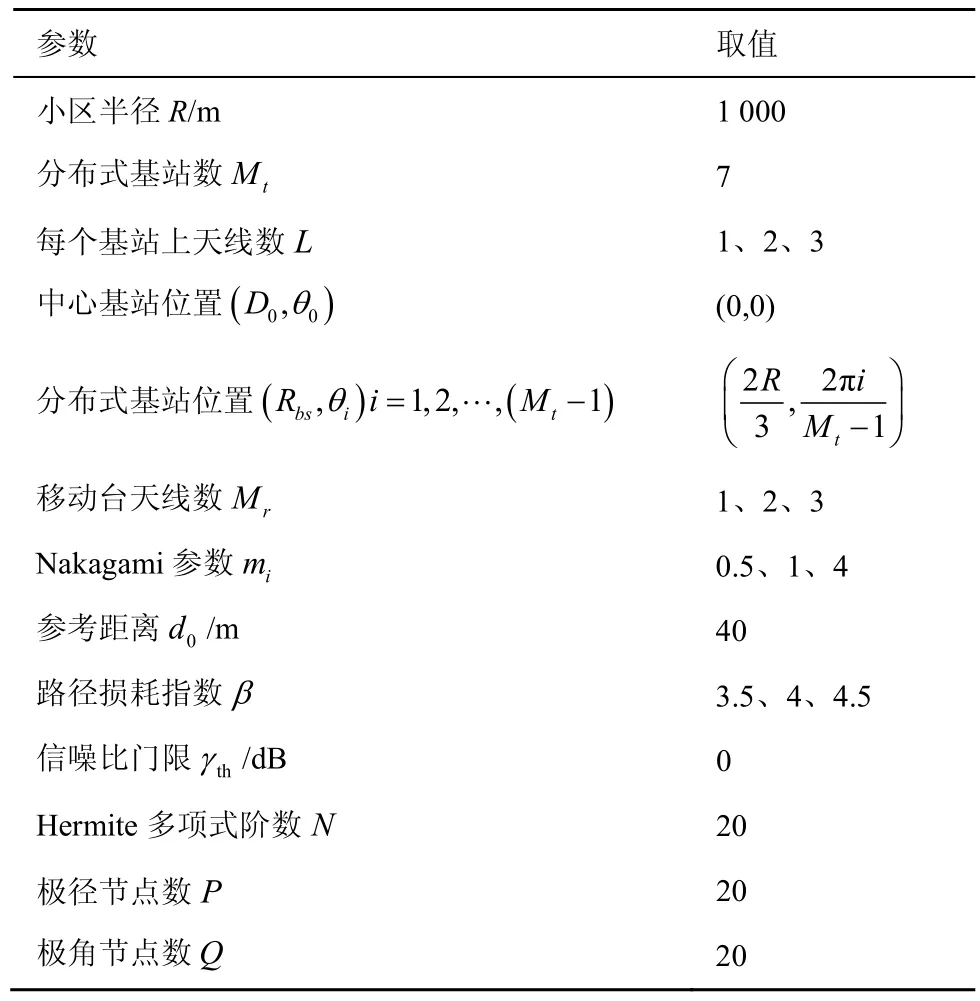
表1 仿真参数

图3～图6分别给出移动台均匀分布和准均匀分布时，不同系统参数下，小区内系统下行平均中断概率随传输信噪比（SNR）变化的情况。从这些图中可以看出：随着传输信噪比的增加，系统平均中断概率单调递减；而在相同条件下，小区内移动台准均匀分布时的系统中断性能比移动台均匀分布时提高很多，这主要是因为2种用户分布模型都被用来分析图1所示的经典分布式MIMO系统，而本文所提准均匀分布模型因能更好地反映用户实际分布情形，故能更好地体现图1分布式MIMO系统分布式基站的放置优点，进而提高用户接入效率、降低系统中断概率。此外，本文推导得到的近似理论值与计算机仿真值之间的误差一直保持在可以接受的范围内，证明本文推导得到的理论表达式具有很好的准确性。

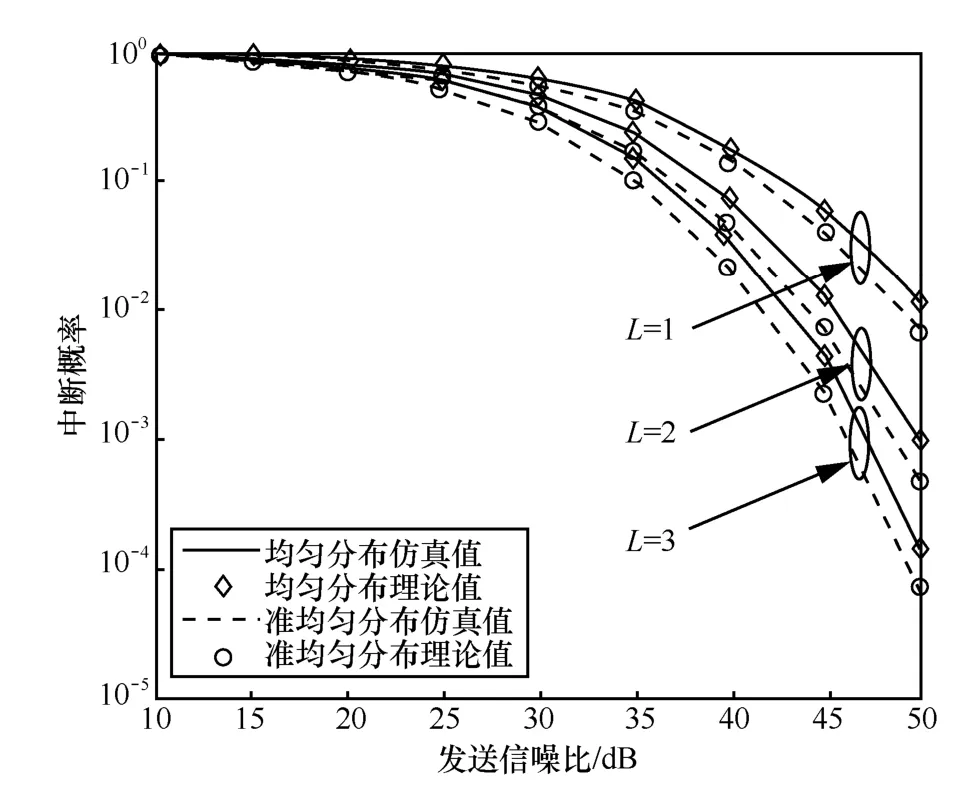
图3 不同分布下，基站所配置天线数的影响

图3给出了移动台均匀分布和准均匀分布时，每个分布式基站上所配置的天线数目对系统下行平均中断概率的影响。图3中仿真曲线表明：随着基站上参与发送天线数目的增多，发送端空间分集度升高；而采用最大比发送机制能够有效地提高信噪比，这些都有效降低了系统下行平均中断概率。

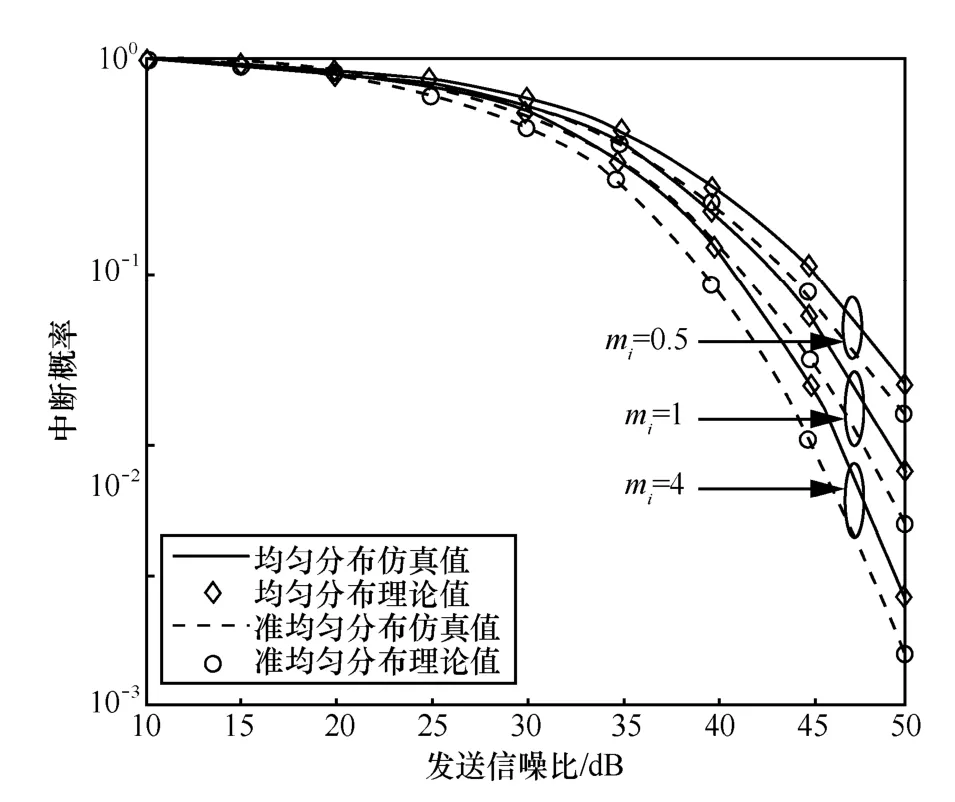
图4 不同分布下，Nakagami参数的影响

图4给出了移动台在小区内均匀分布和准均匀分布时，在不同的Nakagami参数mi取值下，系统下行平均中断概率随发送信噪比变化曲线。随着mi取值的不断增大，无线信道的小尺度衰落越来越弱，移动台接收信噪比随之增大，使得系统下行平均中断概率降低，系统性能得到提高。

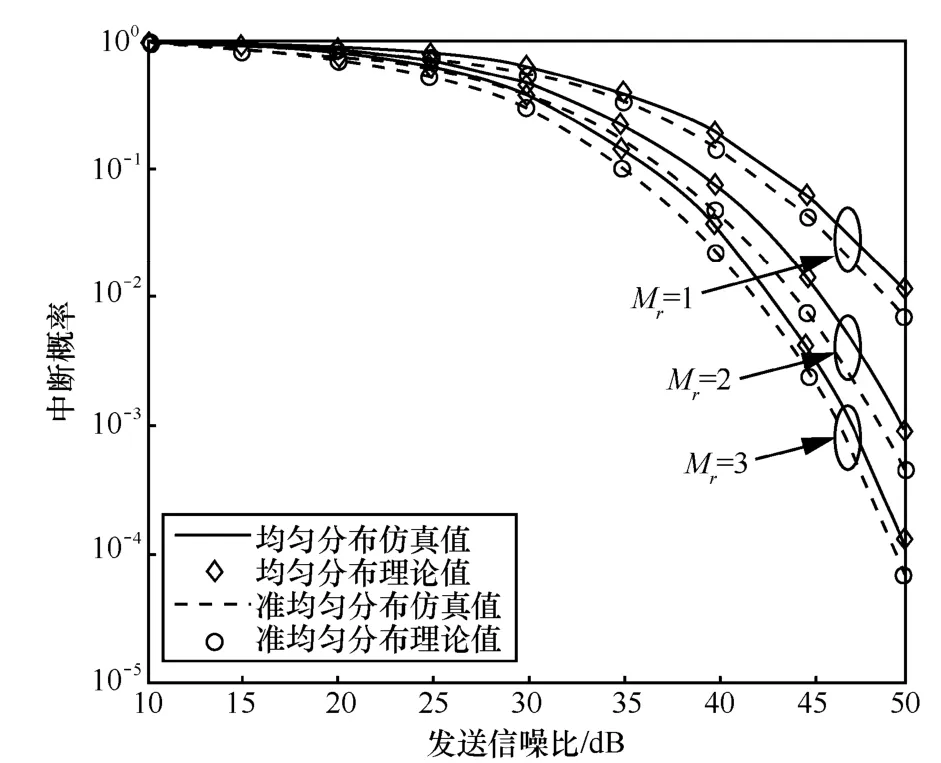
图5 不同移动台分布下，接收天线数目的影响

图5给出了移动台均匀分布和准均匀分布时，移动台接收天线数目对系统下行平均中断概率的影响。图中仿真曲线表明：随着移动台接收天线数的增多，接收端空间分集度升高；在接收端采用最大比合并之后，输出信噪比就越大，因此，系统下行平均中断概率也就越小。

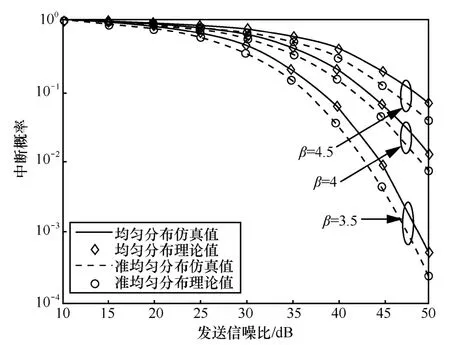
图6 移动台均匀分布时，路径损耗指数的影响

图6给出移动台均匀分布和准均匀分布时，在不同路径损耗指数下，系统下行平均中断概率的变化情况。从图中可以看出，随着路径损耗指数的增大，信号经历的路径损耗愈强，因而接收信噪比减小，最终导致中断概率升高、系统性能变差。

图7给出的是分布式基站天线与中心基站天线之间的归一化距离（Rb/sR）对系统性能的影响。当横坐标取值为0时，即分布式基站与中心基站距离为0，此时为传统的集中式MIMO系统；当横坐标取值大于0时，基站天线实现分开放置，成为所谓分布式MIMO系统。由图中仿真结果可以看出：分布式MIMO系统相比于集中式MIMO系统，在中断概率这一性能指标上有了很大的提高；同时可见分布式基站的放置对系统中断概率亦有很大影响；在不同的移动台分布模型下，要想获得最小的系统下行平均中断概率，Rbs的取值是不同的，这个结论可为后续分布式 MIMO系统基站侧天线的优化配置研究提供理论依据。

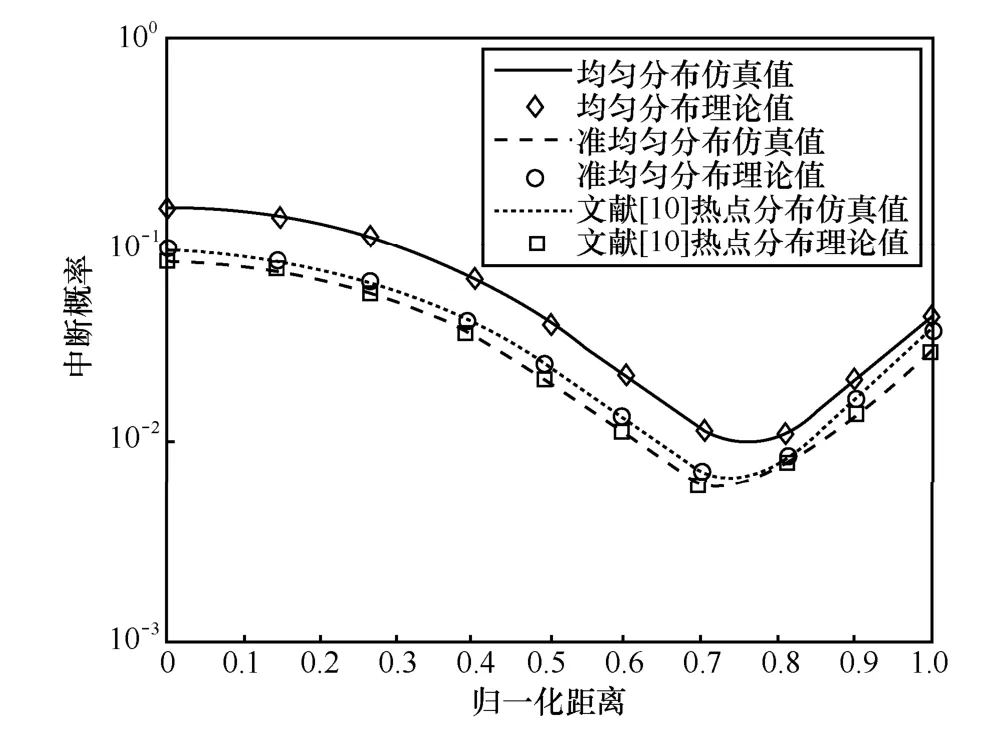
图7 分布式基站与中心基站归一化距离的影响

此外，不同的小区移动台分布模型对系统中断概率的影响也非常明显，相较于传统的小区内均匀分布模型和文献[10]中所研究的分段均匀分布模型，本文提出并详加研究的准均匀分布模型所获得的系统中断概率较前二者都要低，尤其在获得最优中断性能的条件下，相较于前者大约可以降低约40%。

5.2 分析与讨论

最后就分布式 MIMO系统中系统下行中断概率产生重要影响的小区用户分布模型的研究意义或者说研究必要性再稍微展开一些定性的分析与讨论。

从前面的仿真结果可以看出，小区内移动用户的地理位置分布确实对作为分布式 MIMO系统重要系统性能评价指标之一的中断概率产生了很大影响。即便是2个完全相同的网络，比如图1所示同心圆加中心基站的经典分布式MIMO系统，在用户分布不同时，如用户服从小区内均匀分布、或服从文献[10]所提包含用户热点分布的分段均匀模型以及服从本文所研究的准均匀分布等，系统将会产生完全不同的中断概率。这也从一个侧面说明，单纯的系统中断概率并不能完全真实、全面地反映一个现有网络的物理实质。此外，从图7的结果也能非常直观地看出，若以中断概率作为分布式MIMO系统所追求的优化目标，则能得到最佳中断概率的分布式基站端口的放置位置必须要考虑诸如移动用户的地理分布特征这样的统计参量。也就是说，要想基于系统中断概率获得分布式基站端口的最优位置配置，就必须关注移动台的分布特征。

一般来说，用户的地理分布特征虽不会随基站的位置和多少而改变，但基站的数目和放置位置确实反过来又会影响用户相对于基站的相对地理分布，而这种相对分布由上述分析可知，显然会对系统中断概率性能产生不小的影响。本文所研究的不同移动台分布模型针对的正是已有的经典分布式MIMO系统框架结构，也即研究分布式基站位置固定配置在同心圆和小区中心时的系统中断性能。上述一系列仿真结果亦显示这种已有的经典分布式MIMO系统的基站分布模式或设计，从降低系统中断概率的角度，应该更“契合”本文所分析的较符合实际工作环境的“准均匀分布”用户分布；而传统均匀分布或分段均匀分布都将“低估”该经典分布式MIMO系统的中断概率性能优势。本文这一研究成果也进一步说明了这种经典同心圆配置分布式基站的分布式 MIMO系统设计思路对于更符合实际移动用户分布预期的径向线性稀疏模式是成功、合理的。当然，实际用户分布作为一种时变的、非人为可控的客观存在，在这种复杂情况下要获得分布式MIMO系统的最优系统性能（比如最低中断概率、最小误码率乃至最大系统容量等）就需要即时综合用户分布模型等来重新优化设计分布式基站诸如位置、发射功率等参数，这将是另一个更加深入的后续研究课题。

6 结束语

本文在综合考虑包括Nakagami-m衰落、路径损耗和阴影衰落的完善复合信道模型的基础上，提出了一种比较符合小区移动台实际分布的准均匀分布模型，并以发送端采用选择最大比发送、接收端采用最大比合并接收为背景，详细推导了准均匀小区内系统下行平均中断概率的近似闭合表达。数值仿真结果显示该表达式能比较准确地计算分布式基站所配置天线数目、Nakagami-m参数、路径损耗指数以及接收天线数目等系统重要参数对下行中断概率的影响，证明了该中断概率闭型表达式的正确性和合理性；该闭型表达式将为后续分布式MIMO系统小区网络规划方面的工作提供非常重要的理论计算参考。此外仿真还显示，针对经典分布式MIMO系统，不论采用传统均匀分布还是后来的改进型分段均匀分布模型，与本文提出的准均匀分布模型相比，都将高估实际小区移动台分布的中断概率性能，这也从另一个侧面证明了本文所提准均匀分布移动台模型的合理性。

[1]FOSCHINI G J,GANS M J. On limits of wireless communications in a fading environment when using multiple antennas[J]. Wireless Personal Communication,1998,6(3):311-335.

[2]HU H,ZHANG Y,LUO J. Distributed Antenna Systems: Open Architecture for Future Wireless Communications[M]. Auerbach Publications,CRC Press,2007.

[3]ROH W,PAULRAJ A. MIMO channel capacity for the distributed antenna systems[A]. Vehicular Technology Conference[C]. Vancouver,2002.706-709.

[4]HAN S,WANG J,LI V O K,et al. Optimal diversity performance of space time block codes in correlated distributed MIMO channels[J].IEEE Transaction on Wireless Communication,2008,7(6):2106-2118.

[5]RONG Y,HUA Y,SWAMI A. Space-time power schedule for distributed mimo links without instantaneous channel state information at the transmitting nodes[J]. IEEE Transaction on Signal Process,2008,56(2): 686-701.

[6]PHAM T H,NALLANATHAN A,LIANG Y C. Joint channel and frequency offset estimation in distributed MIMO flat-fading channels[J]. IEEE Transaction on Wireless Communication,2008,7(2):648-656.

[7]ROH W,PAULRAJ A. Outage performance of the distributed antenna systems in a composite fading channel[A]. IEEE Vehicular Technology Conference[C]. Vancouver,2002. 1520-1524.

[8]CHEN H M,WANG J B,CHEN M. Outage performance of distributed antenna systems over shadowed nakagami-m fading channels[J].European Transaction on Telecommunications,2009,20(5):531-535.

[9]CHEN H M,WANG J B,CHEN M. Downlink outage probability of distributed antenna systems over shadowed Nakagami-m fading channels with antenna selection[A]. Wireless Communication and Signal Processing[C]. Nanjing,China,2009.1-4.

[10]王俊波,王金元,陈华敏等. 分布式天线系统中的系统下行中断概率分析[J]. 电子学报,2011,39(4):785-790.WANG J B,WANG J Y,CHEN H M,et al. System downlink outage probability analysis in distributed antenna systems[J]. Acta of Electronica Sinica,2011,39(4):785-790.

[11]CHOI W,ANDREW J G. Downlink performance and capacity of distributed antenna systems in a multicell environment[J]. IEEE Trans Wireless Commun,2007,6(1): 69-73.

[12]SIMON MK,ALOUINI M S. Digital Communication over Fading Channels (2nd edn)[M]. New York: Wiley,2005.

[13]GOLDSMITH A. Wireless Communication[M]. New York: Cambridge University Press,2005.

[14]GRADSHTEYN I S,RYZHIK I M. Table of Integrals,Series and Products[M]. San Diego: Academic Press,2007.

[15]PROAKIS J G. Digital Communications (4th edn)[M]. McGraw-Hill Companies,Inc,2001.

[16]ABRAMOWITZ M,STEGUN I A. Handbook of Mathematical Functions with Formulas,Graphs,and Mathematical Tables (9th edn)[M].New York: Dover Publishing Company,1970.

[17]BURDEN R L,FAIRES J D. Numerical Analysis(7th edn)[M]. Boston:PWS KENT Publishing Company,1989.