递归SOQPSK-TG信号的两状态判决反馈解调算法
2014-10-27孙锦华韩会梅
孙锦华,韩会梅
(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)
1 引言
成形偏移正交相移键控(SOQPSK,shapedoffset quadrature phase-shift keying)信号是一种频谱高效的连续相位调制方式,具有包络恒定、功率有效性高等特点[1,2]。在一些功率和带宽双重受限的军事通信、卫星通信、遥测通信等领域中,全响应、部分响应SOQPSK信号已成为UHF卫星通信军标MIL-STD 188-181[3]、航空遥测系统IRIG 106-04标准[4]的建议波形。近年来,研究者对SOQPSK信号的解调、同步、性能限等问题进行了深入的研究[5~11]。
SOQPSK信号是一种连续相位调制(CPM,continuous phase modulation)信号,根据相位关联长度的不同,可分为全响应SOQPSK(如MIL-STD SOQPSK)和部分响应SOQPSK(如SOQPSK-TG)。与MIL-STD SOQPSK信号相比,SOQPSK-TG信号具有更好的功率谱特性。根据 SOQPSK信号的特性,可以将SOQPSK信号的调制分解为预编码与连续相位信号调制2部分,并且根据预编码的形式,可以将 SOQPSK信号分为递归预编码和非递归预编码[12]。SOQPSK信号的这种预编码特性使其内在的记忆特性可以在串行级联编码调制系统中作为内码使用。对于编码级联SOQPSK系统,采用卷积码与SOQPSK的串行级联系统,要求内码SOQPSK必须是递归预编码才能获得较大的编码增益[12],因此这里主要讨论递归SOQPSK-TG信号。
对于递归SOQPSK-TG信号,其相位关联长度L为8,在接收端若采用传统最优的最大似然接收机,则接收机网格需要512个相位状态,运算复杂度极高,在实际工程应用中受到一定限制。
文献[13]应用脉冲截断(PT)技术,使部分响应SOQPSK-TG信号可以像MIL-STD SOQPSK一样建模成四状态的全响应CPM信号。文献[14]给出递归SOQPSK-TG信号的四状态解调器,并将递归SOQPSK-TG信号的差分编码器和预编码器结合起来使网格的状态数达到最少的两状态,得到递归SOQPSK-TG的两状态简化算法,但两状态网格图中的状态变量与相位状态不再存在一一对应的关系,在接收端由状态变量并不能确定当前时刻的累积相位信息,无法恢复当前时刻支路上的标准信号。为此,文献[14]引入判决反馈来解决这个问题,在该接收机中采用Viterbi算法恢复信息序列。
本文首先对递归SOQPSK-TG信号进行了简要介绍,然后介绍了基于脉冲截断的递归SOQPSK-TG信号的四状态解调算法,最后在四状态网格图基础上,通过合理的状态合并,得到递归两状态网格图,并对文献[14]提出的判决反馈算法进行了研究。由于在递归 SOQPSK-TG编码级联系统中需要提取SOQPSK-TG信号的软信息,但文献[14]采用Viterbi解调不便于提取软信息。因此,本文在接收机中采用MAX-LOG-MAP算法恢复信息序列,以实现软信息的提取。
2 SOQPSK-TG信号模型
2.1 CPM信号模型
SOQPSK是连续相位调制(CPM)中的一种特殊调制方式[12],SOQPSK的复基带信号数学表达式为
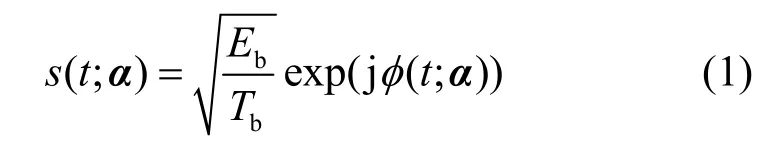
其中,Eb为比特能量,Tb为比特持续时间。φ(t;α)为相位函数,如式(2)所示。
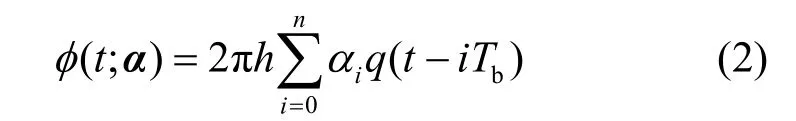
这里αi为实际传输的信息序列,为M进制符号,对于SOQPSK信号,M=3,即 αi∈(-1,0,1);调制指数h=1/2,q(t)为相位脉冲函数,其表达式为
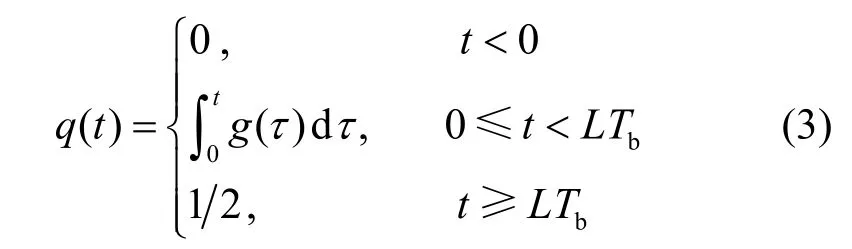
其中,g(t)为频率脉冲,其持续时间为L个比特间隔,当L=1时,为全响应信号;当L>1时,为部分响应信号。
式(2)中的相位函数可另外表示为
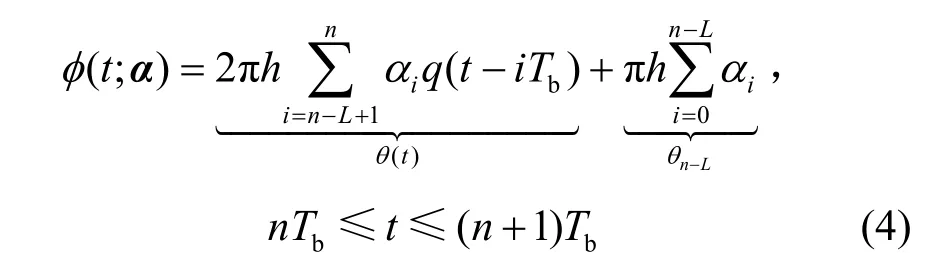

在本文中,讨论的SOQPSK信号体制是采用升余弦频率脉冲成形的部分响应SOQPSK-TG信号。对于SOQPSK-TG信号,其约束长度L=8,频率脉冲成形函数gTG(t)为

幅值A用来归一化脉冲波形,使单个频率脉冲引起的相位偏移为π/2,T1=1.5,T2=0.5,ρ=0.7,B=1.25。图1(a)给出了SOQPSK-TG的频率脉冲函数gTG(t)和相位脉冲函数qTG(t)的波形图。
由图1(a)可看出,虽然SOQPSK-TG信号的频率脉冲函数gTG(t)周期为8Tb,但波形的脉冲宽度较窄且两侧大部分波形接近为0,因此可将关联长度减为L′=1,用周期为Tb的频率脉冲来代替,由此得到的截断相位脉冲函数qPT(t)为
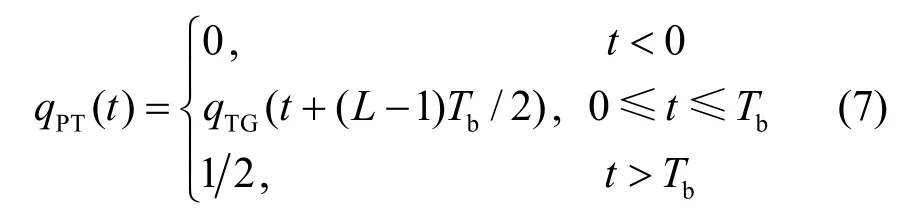
由式(7)可知,qPT(t)是将原相位脉冲函数qTG(t)截断,并将时变部分限制在[0,Tb]间隔内得到的,qPT(t)在间隔[0,Tb]内的波形如图1(b)所示。
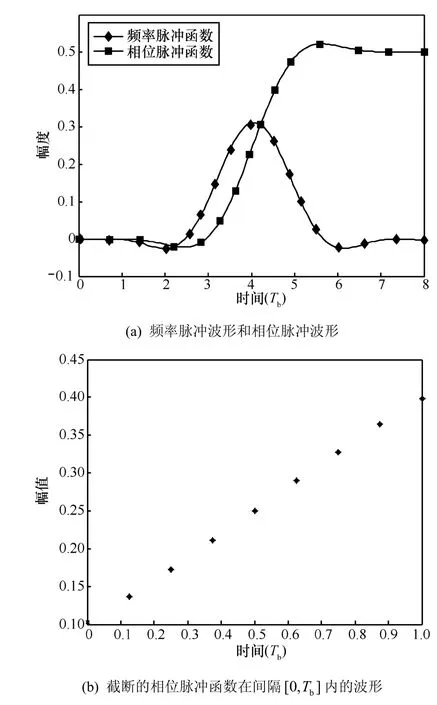
图1 SOQPSK-TG的频率脉冲和相位脉冲函数波形
SOQPSK-TG信号与传统 CPM 的区别在于实际传输的三元符号集{αi}为{−1,0,1}。如图2所示,SOQPSK-TG的调制方式采用预编码与 CPM 调制级联的方案,预编码输出符号集为三元符号集{−1,0,1}。预编码方式分为非递归式和递归式。采用这2种不同方式的预编码,可以分别得到非递归SOQPSK-TG信号和递归SOQPSK-TG信号。下面主要讨论递归预编码方式。
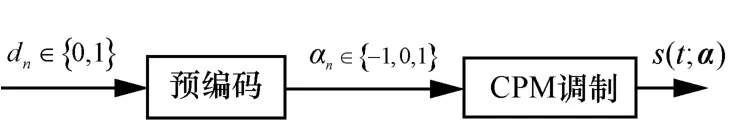
图2 SOQPSK-TG信号的调制方案
2.2 SOQPSK-TG信号的递归预编码
递归预编码实现步骤分为2步,首先将原二进制比特进行差分编码,如式(8)所示,再将差分编码后的二进制比特通过式(9)转化为三进制符号。

由式(9)可知,预编码输出字符的极性会随着奇偶时刻的交替而变化,可以将un-1、un-2和n_ even/n_ odd (偶数时刻/奇数时刻)看作状态的变量,即对应有8个状态来描述的变化转移。将奇偶时刻分开,分别建立网格转移图,构建一个时变的网格图。这样对于单一的奇数时刻(或偶数时刻)只用4个状态即可描述的变化,如图3所示,在每条支路标注的是对应式(9)的递归预编码转变情况,对应为。用一对输入比特来表示状态,对于偶数时刻(I路比特)的状态变量Sn定义为(un-2,un-1),对于奇数时刻(Q路比特)的状态变量Sn定义为(un-1,un-2),状态变量由Sn∈{00,01,10,11}表示。

图3 四状态时变网格
由文献[4]可知,对于递归预编码,网格状态变量Sn与相位状态θn-L存在一一对应的关系,如式(10)所示。
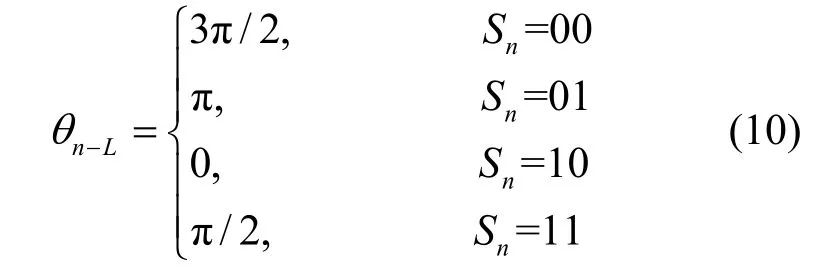
3 简化接收机
3.1 接收信号模型
接收信号表达式为
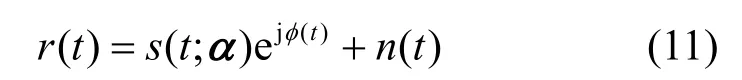
其中,n(t)是均值为零,单边功率谱密度为N0的加性复高斯白噪声;φ(t)是由信道所引起的相位偏移,此处假设φ(t)为0(即相干检测)。由于发送信号s(t;)α的相位具有记忆,因此接收端最优检测器应采用最大似然序列检测。下面对递归SOQPSK-TG信号的解调采用近似简化的方案,减少计算复杂度。
3.2 基于脉冲截断的四状态简化解调算法
文献[12]采用脉冲截断的方法来简化递归SOQPSK-TG的解调复杂度,接收端采用的相位脉冲函数为2.1节所述的qPT(t),qPT(t)可看作一个全响应脉冲,则可将SOQPSK-TG信号看成全响应信号。2.2节所述的预编码中状态变量Sn与相位状态θn-L存在的一一对应关系,使接收端的网格图中不需要全响应CPM的网格图,因此可对SOQPSK-TG信号按图 3所示的四状态网格图,用 MAX-LOGMAP算法解调。
首先根据式(12)计算出每个发送比特的对数似然比。
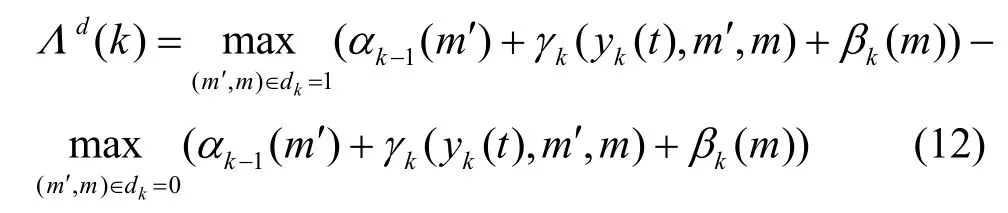
其中,m′为网格中起始状态,m为与起始状态m′相连接的结束状态,dk为第k个输入比特,yk(t)=rk(t+(L-1)Tb/2)是对应的接收信号,αk(m)为前向路径度量,βk(m)为后向路径度量,γk(yk(t),m ′,m)是m′和m之间的状态转移概率。
前向递推式为
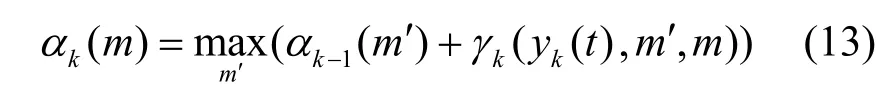
后向递推式为
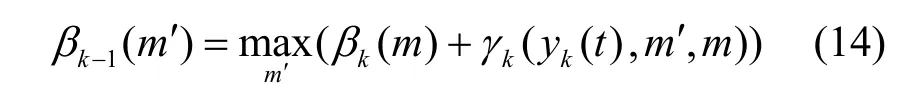
状态转移概率为
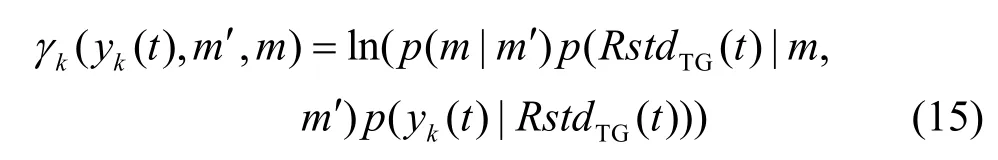
考虑发送比特等概分布,R stdTG(t)为状态转移的输出信号,对图 3,各支路上的状态转移输出信号RstdTG(t)可用简化的相位脉冲来产生表达式为
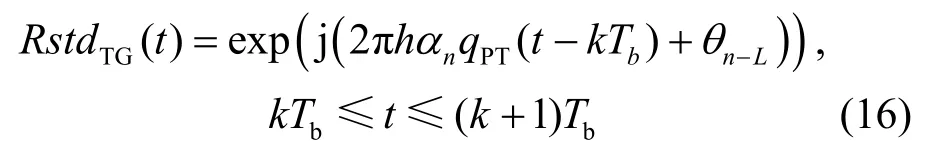
p(R stdTG(t)|m,m ′)=1,在第k个符号间隔,对数转移概率分布为
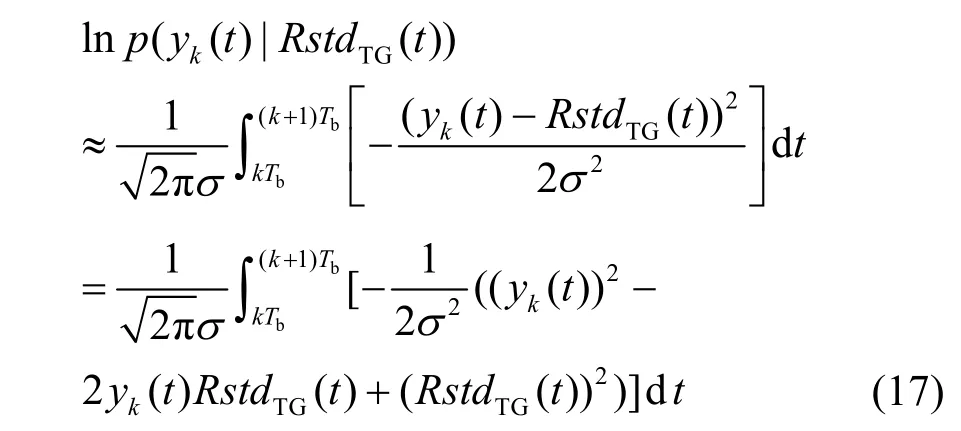
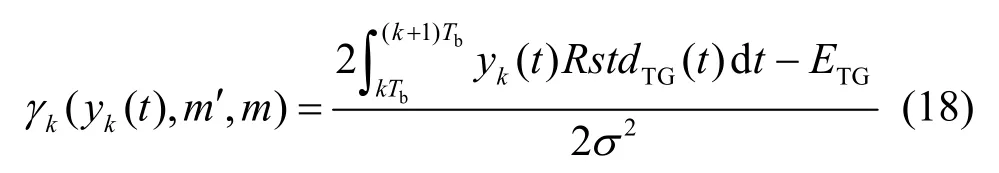
对于按式(18)生成的各支路上的状态转移输出信号 RstdTG(t),每个符号波形的能量ETG是相同的,因此上式中的波形能量可消去。由于按式(12)计算每个发送比特的对数似然比时采用的是求最大值运算,因此信道信息2σ也可消去。因此,对SOQPSK-TG信号对应的状态转移概率可进一步化简为
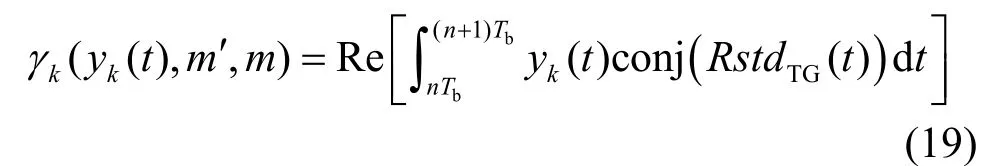
结合 αk(m)、βk(m)并给定初始值,由式(12)计算各发送比特的对数似然值,即软信息,对软信息进行硬判决,即可恢复原始信息序列。
3.3 递归SOQPSK-TG信号的两状态简化解调算法
文献[14]针对递归 SOQPSK-TG信号,提出了两状态简化算法,进一步降低了解调复杂度。将式(8)和式(9)用代数方法合并,得到二进制比特与三进制符号之间的直接对应关系为

其中,状态符号sn由下式更新
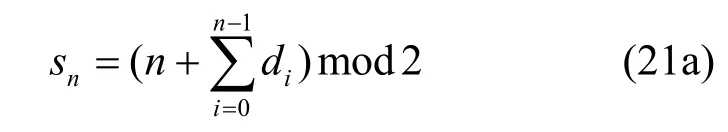
或

由式(20)可知,可以将sn看作状态变量,建立一个两状态网格转移图,如图4所示。
由式(21a)可以得出,该递归两状态网格图是由四状态的递归网格图简化而来的,对I路简化:相同合为0状态,相异合为1状态;对Q路简化:相同合为1状态,相异合为0状态,(“相同”指表示状态的2个比特相同,即00,11状态;同理,“相异”指01,10状态)。
图4中分支上的标注为dn/αn,相对于四状态的时变网格图,两状态时不变网格图具有更为简化的状态表示,但是两状态网格图并没有减少SOQPSK-TG 信号表达式中的累积相位状态θn-L的数量,使两状态网格中的状态变量Sn与相位状态θn-L之间不再存在一一对应的关系。因此,若采用两状态网格图,在接收端由状态Sn当前时刻的累积相位信息并不确定,无法恢复当前时刻支路上的标准信号,即无法通过式(19)计算当前支路的状态转移概率。为此,文献[14]引入判决反馈来克服这一缺点。
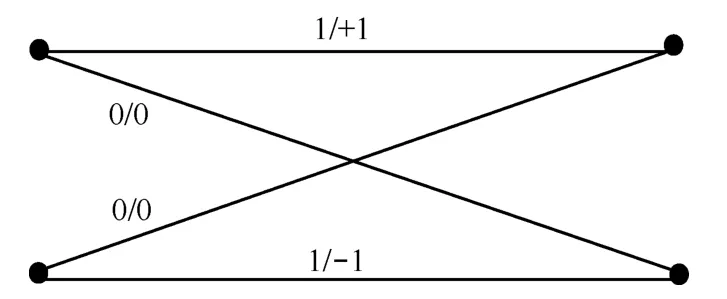
图4 递归SOQPSK-TG两状态网格
如图4所示,当前网格图中起始状态为Sn,结束状态为En,设αn(En)为从Sn到En的幸存路径上的三进制字符,可通过式(22)计算下一状态对应的起始相位值。

其中,θn-1(Sn)为起始状态对应的相位值,即当前网格的起始相位状态θn-1,θn(En)表示当前网格中末状态对应的相位值,且当前网格的末状态即为下一网格的起始状态,即 θn(En)=θn+1(Sn+1)。因此,给定合适的网格状态的相位初始值,通过式(18)进行逐次递归即可计算任一时刻对应网格图中起始状态的相位值,这一相位值即为当前网格图中的累积相位θn-1。结合当前网格图中的累积相位θn-1和式(16),可得到当前网格图中的分支路上的状态转移输出信号 RstdTG(t),通过式(19)计算当前支路的状态转移概率。有了各支路的状态转移概率,利用3.2节的MAX-LOG-MAP解调算法,就可恢复出原始数据序列。
若根据式(10)给定两状态网格图中初始状态相位 θn-1(Sn)的值,则利用式(22)得出的下一状态对应的起始相位值,与四状态网格图的相位值是一样的,因此该判决反馈算法不会丢失四状态网格的相位信息。
4 递归SOQPSK-TG误比特性能分析
以一致界作为AWGN信道上的误比特率上界,对于递归SOQPSK-TG信号,其四状态解调的理论误比特率[14]满足

递归SOQPSK-TG信号两状态解调的理论误比特率[14,15]满足
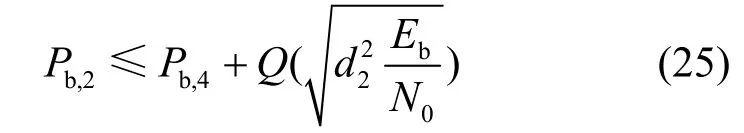
5 仿真结果与分析
以下通过仿真说明递归SOQPSK-TG信号的两状态判决反馈算法的性能,仿真时采用MAX-LOG-MAP算法进行解调。
用3.2节所述的递归SOQPSK-TG四状态算法和3.3节所述的递归SOQPSK-TG两状态判决反馈算法分别对信号进行解调,得到的误比特性能对比如图5所示。图5也给出了四状态算法和两状态判决反馈算法的理论曲线。从图5中可以看出:
1)接收端采用四状态简化解调的解调性能与其理论曲线基本重合,验证了四状态简化解调算法的可行性;接收端采用两状态判决反馈的解调性能与其理论曲线基本重合,验证了两状态判决反馈解调算法的可行性;但发现在高信噪比下仿真曲线与理论性能有微小的差距,这是由于接收端在进行解调时所用到的相位脉冲函数,是通过对发送端的相位脉冲函数进行截断得到的(如图 1所示),相位约束长度由8减小到1,相位信息会有一定的损失,从而对解调性能有一定的影响。
2)四状态简化解调的解调性能比两状态判决反馈解调的解调性能优越,两状态算法在信噪比大于0 dB,误比特率为10−2~10−4时,信噪比有0.1 dB~0.5 dB的损失,这是由于两状态网格图状态变量与累积相位不存在一一对应的关系,需要通过判决幸存路径,获得下一网格的累积相位值,若前一网格判决幸存路径有误,则可能会影响到下一网格内的信息判决,导致错误事件增加,而四状态网格图状态变量与累积相位存在一一对应的关系,可由下一网格的状态变量得到正确的累积相位值。但信噪比越大,由两状态网格判决幸存路径导致的错误事件越少,两者的误比特性能差距越小。
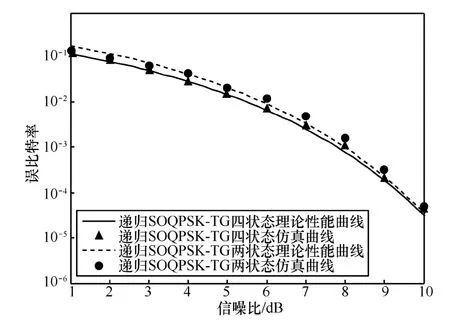
图5 递归SOQPSK-TG两状态和四状态解调性能对比
6 递归SOQPSK-TG信号硬件实现测试结果
以Altera公司的低端FPGA芯片EP2C35F484C6为目标器件,采用硬件描述语言Verilog,开发软件QuartusII 9.0,对四状态简化算法进行实现验证。其中一个信息帧包含1026 bit(包括1024个信息比特和2个归零比特),即513个符号,一个符号采8个样点,采用16 bit位宽量化。
在硬件实现中,调制器可以将发射的标准波形预先存储,根据输入信息比特经过互相关运算形成查找表地址,查表输出波形,较为简单。解调器采用MAX-LOG-MAP算法,主要包括相关模块、前向递推/后向递推模块和软信息提取模块等。相关模块主要完成式(18)和式(19)涉及的积分运算。相关器实质上为一个符号周期内的积分器,即将一个符号周期内接收信号与网格内支路信号的相应样点进行乘、累加运算。每经历一个符号周期,才有I路或Q路的相关值输出,为节省乘法器资源,对I、Q支路接收样点数据进行乒乓操作,每间隔一个符号周期,交替计算I路、Q路的相关值。前向递推和后向递推由MAX-LOG-MAP算法原理可知,一个信息帧中,需要前向路径度量计算完毕后,才开始计算后向路径度量。在实际信息处理中,在开始计算一帧数据的后向度量值时,仍有新的数据帧进入,需要计算新一帧的前向度量值,因此,为了实现流水操作,需要对分支度量值和前向度量值分别进行乒乓缓存,以处理连续帧的接收。
通过QuartusII 9.0的时序分析报告,得出调制器的最小时钟周期为4.241 ns,处理延迟为18个样点时钟,I路和Q路样点同时输出,即输出一个复信号需要8个样点时钟,一个复信号中包含2个比特,因此调制器的处理速率为2/(8×样点时钟),若取样点时钟为6 ns,这样调制器的速率为41.66 Mbit/s。将调制器输出的波形与Matlab定点仿真中的I路、Q路样点输出对比得到两者波形输出是一致的。解调器模块的时序分析报告给出的最小时钟周期为6.376 ns,取样点时钟为8 ns,解调器的的处理时延大约等于一个信息帧的前向度量计算时长,即Tdelay≈2×一帧内符号数×每符号内样点数×样点时钟周期≈2×513×8×8ns=65664ns。解调器的处理速率为Rb=一帧信息比特数/处理一帧数据时长=1024 bit/65.664μs≈15.5 Mbit/s,将解调器的软输出与 Matlab定点仿真中的软信息输出对比得到两者的软信息是一致的。
从四状态简化解调器的硬件测试结果可以推测两状态解调器的情况:由于状态简化仅是在接收端进行处理,因此两者的调制器的处理时延和处理速率是一样的;在接收端,由于两状态网格的状态数是四状态网格状态数的一半,总体运算量减小了一半,因此可以预计两状态解调的处理时延约为四状态解调的处理时延的一半,处理速率约为四状态处理速率的2倍。
7 结束语
针对递归SOQPSK-TG信号两状态网格图状态变量与累积相位不存在一一对应关系的问题,本文对递归SOQPSK-TG信号两状态判决反馈算法进行了研究,并对该算法的性能进行了仿真,仿真结果表明:在信噪比大于0 dB时,两状态判决反馈算法可以获得接近递归四状态解调的误比特性能,与四状态解调算法相比,由于两状态网格的状态数是四状态网格状态数的一半,总体运算量减小了一半,具有较低的运算复杂度,运算复杂度的降低使得解调器的延时减小,提高了解调器解调效率,不仅可以应用于要求实现复杂度低的系统中,而且更有利于工程应用。
[1]SIMON MK,LI L. A cross-correlated trellis-coded quadrature modulation representation of MIL-STD shaped offset quadrature phase-shift keying[EB/OL]. http://ipnpr.jpl.nasa.gov/progress_report/42-154/154J.pdf,2003-08-15.
[2]LI L,SIMON MK. Performance of coded OQPSK and MIL-STD SOQPSK with iterative decoding[J]. IEEE Trans on Communication,2004,52(11):1890-1900.
[3]AEGNCY D I S. Department of Defense Interface Standard,Interoperability Standard for Single-Access 5 kHz and 25 kHz UHF Satellite Communications Channels[R]. 1999.
[4]Range Commanders Council Telemetry Group. Telemetry standards IRIG standard 106-04 Part I[S]. 2004.
[5]SAHIN C,PERRINS E. The capacity of SOQPSK-TG[A]. IEEE Military Communications Conference[C]. Baltimore,MD,USA,2011.555-560.
[6]HOSSEINI E. PERRINS E. The Cramér-Rao bound for data-aided synchronization of SOQPSK[A]. IEEE Military Communications Conference[C]. Orlando,Florida,2012.1-6.
[7]孙锦华,朱吉利,吴小钧.导频和软信息联合辅助的短突发SOQPSK载波同步[J]. 西安电子科技大学学报,2013,40(4):16-23.SUN J H,ZHU J L,WU X J. A joint pilot and soft information assisted carrier synchronization for short burst SOQPSK signals[J]. Journal of Xidian University,2013,40(4):16-23.
[8]SUN J H,ZHU J L,WU X J. A joint pilot and demodulation soft information carrier synchronization for SOQPSK signals[A]. The 5th Global Symposium on Millimeter Waves (GSMM)[C]. Harbin,China,2012. 512-516.
[9]BALASUBRAMANIAN U,PACHAME P R ,RADHAKRISHNA P,et al. Telemetry applications of SOQPSK and GMSK based modulation for airborne platforms[A]. 2012 International Conference on Communications,Devices and Intelligent Systems (CODIS)[C]. Bangalore,India,2012.17-20.
[10]HOSSEINI E,PERRINS E. FPGA Implementation of a coherent SOQPSK-TG demodulator[A]. IEEE Military Communications Conference[C]. Baltimore,MD,USA,2011.471-476.
[11]WILLIAMS I E,SAQUIB M. Linear frequency domain equalization of SOQPSK-TG for wideband aeronautical telemetry channels[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(1):640-647.
[12]PERRINS E,RICE M. Reduced-complexity approach to iterative detection of coded SOQPSK[J]. IEEE Trans on Communication,2007,55(7):1354-1362.
[13]SVENSSON A,SUNDBERG C E,AULIN T. A class of reduced complexity viterbi detectors for partial response continuous phase modulation[J]. IEEE Trans on Communication,1984,32(10): 1079- 1087.
[14]PERRINS E,KUMARASWAMY B. Decision feedback detectors for SOQPSK[J]. IEEE Trans on Communications,2009,57(8): 2359-2368.
[15]NELSON T,PERRINS E and RICE M. Near optimal common detection techniques for shaped offset QPSK and Feher’s QPSK[J]. IEEE Transactions on Communications,2008,56(5): 724-735.
