可证安全的高效可托管公钥加密方案

刘文浩，王圣宝，曹珍富，韩立东

(1. 杭州师范大学 信息科学与工程学院，浙江 杭州 310012；2. 上海交通大学 计算机科学与工程系，上海 200240)

1 引言

N=1公钥密码学在网络信息安全中的作用越来越受到人们重视，它能够同时为用户提供保密性和抗抵赖（数字签名）服务[1]。然而，利用唯一一个公钥/私钥元组来同时提供这 2种服务的做法存在严重问题。首先，为了防止由于用户私钥的丢失而造成对先前密文的不可解密，或者出于法律监管的需要，往往要求用户将解密私钥托管到可信任的托管中心(EA,escrow agency)。其次，对于数字签名服务而言，出于满足真正意义上的不可抵赖性的目的，又要求签名私钥应该只能为签名人所掌握，即托管中心不能够获得用户的(签名)私钥。所以，当使用传统公钥加密方案(例如RSA)时，由于解密私钥与签名私钥相同，用户的唯一私钥是否被托管就是一个矛盾。

现行公钥基础设施(PKI,public key infrastructure)为了调和这个矛盾，一般采用“双证书模式”[2]，即让每个用户使用2对公/私钥。2个公钥分别被2份公钥证书所证实。然而，这种做法的最大问题在于它使得PKI 所颁发的证书数目加倍，极大增加了其证书管理负荷。并且，这种模式也增加了用户端自身负担：每个用户必须存储和管理2个私钥，即解密私钥和签名私钥。

2001年，Verheul[3]提出的可托管公钥加密(E-PKE,escrowable public-key encryption)方案成功解决了上述难题。它的基本思想是，解密权能够在不牺牲数字签名服务的前提下被托管。在这种全新加密方案中，用户的唯一公钥对应于2个解密私钥：自己掌握的主解密私钥(primary decryption key)，记为KP；可交给托管中心的托管解密私钥(escrow decryption key)，记为KE。其中，主解密私钥不能够被托管中心利用托管解密私钥计算出来。此时，用户利用其主解密私钥 KP进行的数字签名就满足法律意义上的不可抵赖性。这种方案被分成如下2类。

1)主动方案：用户能自主决定是否将托管解密私钥 KE托管。显然，如选择托管，用户需要通过安全信道首先将托管解密私钥KE交付给托管中心。例如，Verheul[3]提出的第1个此类方案就是主动式方案。

2)被动方案：也称为全局托管方案。用户不能自主选择是否将解密权托管。托管中心能依靠其唯一托管解密私钥（也即系统主私钥），解密系统中所有用户的密文。Boneh 和 Franklin[4,5]提出的E-PKE方案就属于被动式方案。

2 相关数学基础知识

本文所讨论的全部方案都基于双线性映射(bilinear pairing)。因此，这里有必要首先回顾相关难题假设，然后给出双线性映射的定义。

定义1 (离散对数难题(DLP,discrete logarithm problem))。假设(G,·)表示一个阶为q的群，g 是它的生成元。离散对数难题是：给定随机元素y∈RG，找到一个数x∈Zq，使得 y=gx。

定义2 (计算性 Diffie-Hellman 难题(CDHP,computational Diffie-Hellman problem))。假设(G,·)表示一个阶为q的群，g表示它的生成元。计算性Diffie-Hellman难题是：给定一个随机三元组(g,ga,gb)，其中，元素，计算 gab。

定义3 (判定性 Diffie-Hellman 难题(DDHP,decisional Diffie-Hellman problem))。假设(G,·)是一个阶为q的群，g为其生成元。判定性 Diffie-Hellman 难题是：给定三元组(ga,gb,gc)，其中，随机元素，判断 gc=gab成立与否。

概略地说，离散对数(DL)、计算性 Diffie-Hellman (CDH)以及判定性Diffie-Hellman (DDH)假设指的是：不存在概率多项式时间算法能够以不可忽略的优势解决DLP、CDHP 或DDHP 难题。

假设G1是由生成元 P 生成的循环群，其阶为素数q，令G2代表另一个阶也是q的循环群。令群G1与G2上的离散对数难题假设成立。

定义4 (双线性映射(Pairing))。双线性映射e是双线性函数e: G1×G1→G2，它符合以下性质。

1)双线性：如果P,Q∈G1并且，那么e(a P,b Q)=e(P,Q)ab。

2)非退化：满足 e(P,P)=1。

3)可计算：如果P,Q∈G1，则 e(P,Q)∈G2是可在多项式时间内计算的。

3 提出的新方案

这里给出本文新提出的2个可托管公钥加密方案。值得特别指出的是，为了节省篇幅，省略了对可托管公钥加密方案的形式化定义。相关定义与其他类别的公钥加密方案极其类似，例如 Boneh 和Franklin[4,5]所给出的关于基于身份的加密方案的形式化定义。不同之处仅在于，可托管公钥加密方案中用户的私钥有2个，相应地，解密算法也有2个。

3.1 第1个新方案

本文第1个新方案来源于Boneh-Frankin[1,2]被动式方案。不同之处在于将它转化为主动式方案。

系统初始化(Setup)：给定安全参数 k，进行以下步骤计算。

1)输出 2个阶为素数q的循环群G1与G2、群G1的生成元P，以及双线性映射 e: G1×G1→G2。

2)选择杂凑函数H: G →{0,1}n，其中，n是整数。此方案的明文空间是 M={0,1}n，密文空间是。系统公共参数 params为(q,G1,G2,e,n,P,H)。

私钥生成(Key-Gen)：每个用户可按如下算法生成自己的公/私钥元组。

1)随机选择 2个随机数 x1,x2∈Zq，并把其中任意一个设置为主解密私钥，这里假定主解密私钥KP=x1。

2)托管解密私钥：KE=x2。

3)用户公钥为P1=x1P及 P2=x2P∈G1

加密算法(Encryption)：为了加密消息m∈M，加密方首先选择 r∈Zq，把密文设为C=(r P,m⊕H(gr)),其中 g=e(P1,P2)∈。

解密算法(Decryption)：密文 C=(U,V)，利用自己的主解密私钥x1计算 m=V ⊕ H(e(U,x1P2))。

托管解密(Escrow-Decrypt)：对于密文C=(U,V)，托管中心利用托管解密私钥KE计算m=V ⊕H(e(U,KEP1))。

方案正确性：这个方案的加解密正确性基于如下事实，解密者和托管中心双方都能正确地由密文C的前半部分U计算获得加密方用于对明文m进行加密的会话密钥，即 e(U,x1P2)=gr。同样，e(U,KEP1)=gr。

不同于一般意义上的可托管公钥加密方案，这里用户的唯一公钥(由1P和2P双元组组成)还对应于另外1个解密私钥——第3个解密私钥x1x2P。用户也可以把私钥x1x2P作为托管解密私钥交付给托管中心。如果这样，用户握有的两对公/私钥元组(x1,P1)和(x2,P2)都可以作为签名私钥/验证公钥元组，用来提供抗抵赖服务。

3.2 第2个新方案

本文提出的第2个方案是主动式的可托管公钥加密方案。它的基本过程描述如下。

系统初始化(Setup): 给定一个安全参数k，执行下面的步骤。

1)输出2个阶为素数q的循环群G1与G2、群G1的生成元P，以及双线性映射 e: G1×G1→G2。

2)计算 g2=e(P,P)。

3)选择杂凑函数H: G2→{0,1}n，其中n是整数。

此方案的明文空间是 M={0,1}n，密文空间是C=。系统公共参数 params为(q,G,1G2,e,n,P,g2,H)。

私钥生成(Key-Gen)：这是用户的（双）私钥生成算法。每个用户生成自己的公钥及其对应的2个解密私钥。

1)首先，随机选择一个随机数x∈Zq，并将其设置为主解密私钥，即KP=x。

2)将托管解密私钥设为KE=x-1P。

3)将公钥设为PPub=xP∈G1。

加密算法(Encryption)：对消息m∈M进行加密，加密方首先选择 r∈Zq，接着计算得到密文：C=(r PPub,m ⊕ H(g2r)。

解密算法(Decryption)：收到密文 C=(U,V)，解密方利用KP进行如下计算获得明文：m=V ⊕ H2(e(U,KP-1P))。

托管解密算法(Escrow-Decrypt)：托管中心得到密文 C=(U,V )后，使用KE进行如下计算获得明文：m=V ⊕ H2(e(U,KE))。

4)方案的正确性：此方案的正确性源自于这一事实，无论是用户自己（解密方）还是托管中心，都能够通过密文C的前半部分U计算获得加密方用于加密明文m的会话密钥，即=e(U,KE)=g2r。

方案满足主私钥安全性：托管中心获得的托管解密私钥为KE=x-1P，而由用户唯一掌握的主解密私钥为KP=x，因此，从托管解密私钥计算获得主解密私钥，等价于群G1上的离散对数难题。

3.3 效率和实用性

通过表1来说明本文所提出方案的高计算效率和强实用性。

表1 E-PKE方案间的比较

首先来分析加密方的计算效率。在本文所提出的第2个方案的加密过程中，加密方不需要计算任何双线性映射，也即加密方无论是在线还是离线阶段都无需进行双线性映射函数的计算。在现有的总共4个方案中，只有Verheul方案[3]也满足这样的高计算效率，而其他2个方案中的加密方都需要在线地（也即获得了解密方的公钥，或公钥证书之后）计算一个双线性映射。进一步，第 2个方案比Verheul的方案更加实用，这是因为本文的方案中，加密方在以某种方式获得解密方的公钥之前，就能够首先利用系统公共参数计算得到用于加密明文消息的会话密钥 g2r，其中r为加密方选择的一个随机整数（可离线选定并存储备用）。这意味着明文可以被预先加密。换句话说，密文C的后半部分V可在离线阶段提前得到计算。这大大提高了加密效率。而在Verheul方案中，要求加密方在获得解密方的公钥PPub之后，方能进行会话密钥的计算。其中，r也是加密方选择的一个随机整数（也可离线选定并存储备用）。

而在其他方案方面，在Boneh-Frankin 方案和本文所提出的第1个方案中，加密方在加密时必须在线地（即获得解密方的公钥之后）完成双线性映射的运算。

其次，来看密钥的长度。本文所提出的第2个方案中的用户主解密私钥的长度达到了最优，即为Zq中一个整数的长度。而在公钥的长度方面，Verheul 方案是群G2中的单个元素，相比而言，本文所提出的第2个方案中，其值为群G1中的单个元素。一般来说，后者的长度要短于前者。

3.4 第2个方案的可证明安全性

众所周知，利用由日本学者Fujisaki 和Okamoto所提出的通用转化方法[7]，能够很方便地把达到选择明文安全性的公钥加密方案，增强为达到选择密文安全性的方案。因此，这里只给出了方案的选择明文安全性证明。由于本文所提出的第2个方案是全部现有同类方案中最为高效和实用的。因此，这里只给出对它的安全性证明。类似地，也能够给出其他方案的安全性证明。

为了节约篇幅，省略了对可托管公钥加密方案的形式化安全模型的描述。这一安全模型与传统公钥加密方案的形式化安全模型并无特殊差异。这主要是因为：首先，解密私钥的增加并不会降低方案的安全性，换句话说，所有解密私钥的总体可被看作传统公钥加密方案中的唯一私钥，都是需要被严格保密的；其次，由于托管中心获得了被托管的托管解密私钥，因此它具有同等的解密能力。它不能被看作可能的敌手。

接下来，给出该方案选择明文安全性所基于的难题假设：逆BDH (iBDH)难题假设。

定义5 逆Diffie-Hellman (iBDH)问题)。令群G1、G2、生成元P以及e与前文所定义的同名参数相同。(G1,G2,e)上的 iBDH问题为：假设有(P,a P,b P)，其中，随机的元素，计算

非严格地说，逆 BDH (iBDH)难题假设即逆BDH (iBDH)难题是难解的，即不存在多项式时间算法能计算这一问题。值得指出的是，Zhang等人[8]给出了iBDH 难题假设与标准双线性Diffie-Hellman(BDH)难题假设相互等价的证明。以下定理给出了第2个方案的选择明文安全性。

定理1 假设存在一个优势为ε的敌手A，它是针对该方案的选择明文攻击敌手，假设它最多进行q2次 H 询问，则可构造出一个算法 B，它能以不小于 2ε/q2的优势成功破解iBDH 难题。

证明 假设敌手 A针对 H2最多定下q2次询问，其成功优势是ε。下面，详细构造算法 B，它借助运行敌手A并与之进行交互来成功解决iBDH难题。

假设 B的初始输入值为(q,G1,G2,e)和(P,aP,bP)。用来代表对应于该难题输入的iBDH 难题的解。

初始化：B将公钥设定成(q,G1,G2,e,PPub,n,P,H )，其中，PPub=aP。敌手A 首先获得公钥。这里，未知的解密私钥是 a-1P。后续证明过程中，H为B所完全掌握的随机Oracle。

H-查询：为了模拟敌手A对随机OracleH的询问，算法B维护一个列表(称为H-表)，其格式为(Xj,Hj)。面对询问X，算法B首先检查它是否已经存在于H-表之上。若存在，则算法B返回相应记录中的H值。否则，从{0,1}n中随机选择一个H值返送到敌手A，并把条目(X,H)添入H-表。

挑战：当上述第一阶段结束后，敌手A输出2个明文消息M0、M1，它们的长度相同。算法B随机选择t∈{0,1}和串 S∈{0,1}n，接着，把针对明文消息的加密 C*设定为C*=(U,V)，其中，U=bP，V=Mt⊕ S 。算法B将挑战密文 C*传递给敌手A。

如前所述，a-1P是任何一方都未知的解密私钥，D是算法B所面临的iBDH问题的解。注意，对密文 C*进行解密，得到的结果为V ⊕H(e(a-1P,bP))=V ⊕ H(D)。

猜测：敌手 A在获得密文 C*后，仍然可以发起H-询问。过后，敌手A输出关于比特值t的猜测t∈{0,1}。

输出：最后，算法B随机地从H-表上摘下一个条目(Xj,Hj)并输出其中的Xj作为它的 iBDH难题解。

显然，算法B的上述模拟过程对于敌手来说是完美和不可区分的。因此，得出结论：敌手A的成功优势为ε。将H表示为如下事件：在算法B的模拟过程中，敌手 A以D作为输入，询问随机OracleH。

由于H(D)的值是敌手A无法预测的，所以，如果它在没有针对H询问D，则它也无法预测挑战密文 C*的解密输出。因此有如下结论：在攻击模拟游戏中 Pr[ t=t'|-H]-1/2。

依据关于敌手 A的定义，在真正的攻击中(以及在针对它的模拟中)，|Pr[ t=t′|-H]-1/2|≥ε。关于 Pt[ t=t′]，可得到以下界值

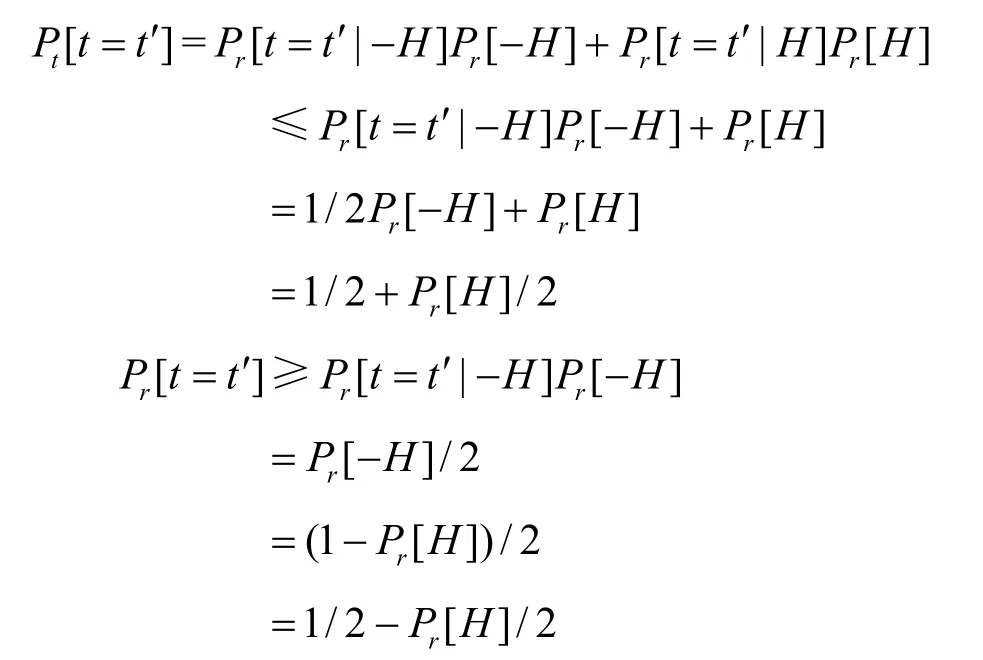
因此有：|Pr[ t=t′]-1/2|≤Pr[ H ]/2。又由于|Pr[ t=t']-1/2|≥ε，因此有：Pr[ H]≥2ε。依据H的定义可推出D出现在H-表中的概率不小于2ε。进一步，算法B求得正确的iBDH 难题实例解的概率不小于 2ε/q2，这与假设iBDH 问题是难解的假设矛盾。

4 结束语

可托管公钥加密方案是一种具有很好应用前景的新型加密方案。特别是随着同样利用双线性映射所构造的基于身份的加密方案被逐步应用[9]，可托管公钥加密有望成为解决现行公钥基础设施中证书管理负担过重问题的一种有效解决方案。本文提出了2个新的此类方案。其中，第二个方案的加密过程最为高效，并且它允许加密方能够以离线方式提前加密明文。最后，详细给出了它的安全性证明。本文所给出的方案是在随机预言模型中安全的，是否存在标准模型下安全的此类方案，值得进一步研究。

[1]ZIMMERMANN P. Pretty Good Privacy―Public Key Encryption for the Masses,PGP User’s Guide[M]. Cambridge,MA: MIT Press,1995.

[2]SANTESSON S,POLK W,BARZIN P,et al. Internet X.509 Public Key Infrastructure,Qualified Certificates Profile,RFC 3039,IETF[S].2001.

[3]VERHEUL E R. Evidence that XTR is more secure than supersingular elliptic curve crypto systems[A]. Proc of Eurocrypt'01[C]. Springer,2001.195-210.

[4]BONEH D,FRANKLIN M. Identity-based encryption from the weil pairing[A]. Proc of CRYPTO'01[C]. Springer,2001.213-229.

[5]BONEH D,FRANKLIN M. Identity-based encryption from the weil pairing[J]. SIAM J Computing,2003,32(3):586-615.

[6]ELGAMAL T. A public key cryptosystem and signature scheme based on discrete logarithms[J]. IEEE Trans Inf Theory,1985,31(4):469-472,

[7]FUJISAKI E,OKAMOTO T. How to enhance the security of public-key encryption at minimum cost[J]. IEICE Trans Fundamentals,2000,9(1): 24-32.

[8]ZHANG F,SAFAVI-NAINI R,SUSILO W. An efficient signature scheme from bilinear pairings and its applications[A]. Proc of PKC'04[C]. Springer,2004.277-290.

[9]LYNN B. On the Implementation of Pairing-Based Cryptography[D].Stanford University,2006.