面向XML关键字查询的高效RKN求解策略

陈子阳，王璿，汤显

（1. 燕山大学 信息科学与工程学院，河北 秦皇岛 066004；2. 河北省计算机虚拟技术与系统集成重点实验室，河北 秦皇岛 066004；3. 燕山大学 经济与管理学院，河北 秦皇岛 066004）

1 引言

随着XML（extensible markup language，可扩展标记语言）应用领域的不断扩展，以XML格式表示和存储的数据量不断增大。作为一种简单易用的信息检索机制，基于XML数据的关键字检索技术得到了研究者的广泛关注[1～16]，其中的核心问题之一是如何高效返回满足特定语义的查询结果[3,5～11]。

通常情况下，把一个XML文档看成一棵带有节点标注信息的文档树T。给定一个关键字查询Q，每个查询结果tv为T中满足查询条件的结果子树，tv包含Q中的所有关键字且tv的根节点v满足特定语义如 SLCA[6～10]，ELCA[3，10～11]等。现有的子树构建方法[12～14]涉及3个步骤。步骤1：遍历倒排表中所有节点，求解相应的SLCA/ELCA节点集。步骤2：再次遍历倒排表，求得与每个 SLCA/ELCA节点v相关的关键字节点集Rv。步骤3：对于每一个Rv，构建满足特定约束条件的结果子树[12～14]。目前，XML关键字查询处理的研究主要集中在如何提高步骤1的处理效率[3,5～11]，实际上，步骤2和步骤3是影响系统整体性能的关键因素。

以 MaxMatch算法[12]为例，在582 MB的XMark注1http://monetdb.cwi.nl/xml。数据集上运行96个查询，这些查询依据其结果选择率注2选择率定义为结果个数和最短倒排表的比值。分成6组。图1给出基于不同算法[7～9]求解SLCA时，步骤1耗费时间占总时间的百分比。图2给出步骤2和步骤3所耗时间的比例关系。根据图1和图2，有如下观察结果。

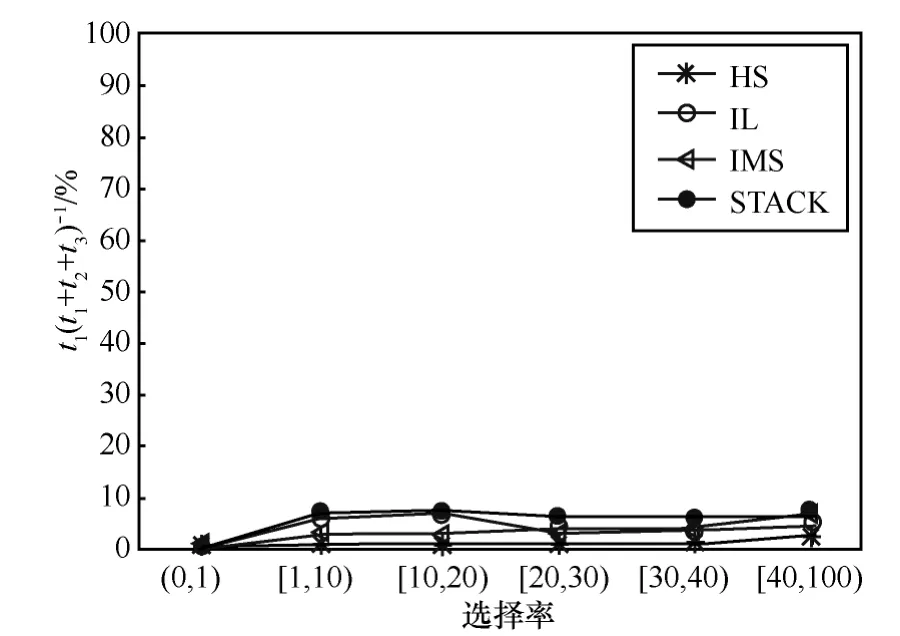
图1 步骤1耗费时间(t1)占总时间(t1+t2+t3)的百分比

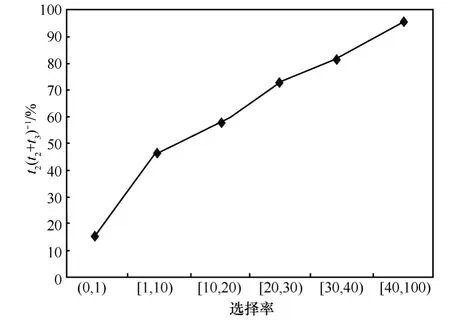
图2 步骤2和步骤3所耗时间的比例关系

观察 1：相对于总时间(t1+t2+t3)而言，步骤1所耗时间(t1)几乎可以忽略不计(小于10%)。

观察2：当结果选择率较低时，步骤3耗费时间(t3)较多，随着结果选择率的增加，步骤2耗费时间(t2)所占比重逐渐增加。

通过上述的2个观察不难发现，无论步骤1采用何种算法，系统整体性能始终受限于步骤2和步骤3。本文重点研究基于ELCA语义如何提高步骤2的处理效率。原因有2个方面：1)已有研究[17]表明，50%的关键字查询是探索式查询，即用户不知其具体查询目的。和SLCA相比，求解ELCA能够返回更多有意义的结果[6,11,15]，有助于用户发现所需信息。2)已有方法[13]的步骤2不能正确求解与每个ELCA节点相关的关键字节点集，导致结果子树可能包含无用信息或丢失有用信息。当然，本文方法适用于SLCA语义。

图3表示XML文档D对应的文档树T。假设要从T中查找Yanshan大学的Tom在Computer期刊上发表的有关XML的文章，可以使用关键字查询Q=｛Yanshan，Tom，Computer，XML｝来完成该查询任务。根据ELCA语义，满足条件的子树根节点为2和7。在判断节点2是否为ELCA节点时，节点6、18、20、21是被排除在外的，即对节点2来说，节点6、18、20、21是无关节点，因此2的相关关键字节点集为R2={3，4，22，23}。然而文献[13]得到节点2的相关节点集为R2={3，4，22，23，6，18，20，21}。如果用户想要得到匹配子树[14]，则用 R2={3，4，22，23，6，18，20，21}构建以节点 2为根的子树时，将包含无用信息(节点 5，6，16，18，19，20，21)，且丢失有用信息（节点 4和 23）。

本文的主要贡献如下。

1)提出相关关键字节点（RKN，relevant keyword node）的形式化定义。

3)针对 RKN-Base算法不能避免处理无用节点的问题，提出优化算法RKN-Optimized。该算法基于每个ELCA节点求其相关关键字节点，可以避免访问无用节点，将时间复杂度降为O(d m| E LCASet|·log|Lm|)，其中，Lm为最长倒排表。

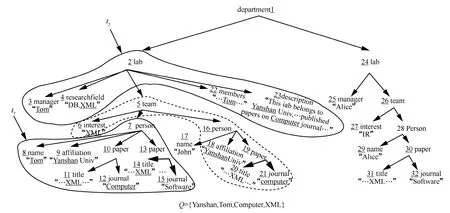
图3 XML文档D对应的文档树T(每个节点旁边的数字是其ID编码，该编码是按照文档顺序排序的)

4)通过实验对算法的性能进行了验证和分析。

2 背景知识及相关工作

2.1 数据模型

本文用带有节点标注信息的树表示一个 XML文档，其中节点表示元素或者属性，边表示节点间的直接嵌套关系。给定查询Q，若节点v的标签、属性或者v的文本包含Q中的关键字k，则称v直接包含k，v为关键字节点。

为了加速查询处理，通常需要给XML文档树中的每个节点v指定一个可以唯一标识的编码，用于确定节点间的位置关系，已有方法通常使用Dewey[16]编码来标识节点。给定节点 v，Dewey编码由其父亲节点的 Dewey编码和其本身在兄弟节点中的顺序值组成。如图3所示，给每个节点一个ID值，该值等于以先序遍历方式访问D时该节点的访问次序。相应地，图3中每个节点v的Dewey编码由根节点到v的路径上所有节点的ID构成，称这种由节点ID构成的Dewey编码为IDDewey编码。

后续讨论中，除非有歧义，本文不对一个节点的ID值及其编码进行区分。例如，图4中的节点9，即为节点 1，2，5，7，9。对于给定的2个节点 u和v，其位置关系包括：文档顺序(≺d)，相等关系(=)，祖先后代关系(≺a). u≺dv表示在文档中，u位于v的前面，即节点u的ID值小于节点v的ID值，称u小于v，反之称u大于v。u≺av表示u是v的祖先节点。如果u和v表示同一个节点，则u=v，并且同时成立。

2.2 查询语义及符号

给定查询Q={k1，k2，…，km}，XML文档D及ki的倒排表Li，Li中的编码按照文档顺序升序有序。图3中查询Q={Yanshan，Tom，Computer，XML}的倒排表如图4所示，图4中的Pos表示倒排表中每个编码的下标位置。假设lca (v1，v2，…，vm)表示节点 v1，v2，…，vm的最低公共祖先(LCA,lowest common ancestor)，则 Q在D上的 LCA集合定义为LCASet=LCA(Q)={v| v=lca(v1,v2,…,vm),vi∈Li(1≤ i≤m)}。例如图3中满足Q={Yanshan，Tom，Computer，XML}的LCA节点为1，2，5，7。

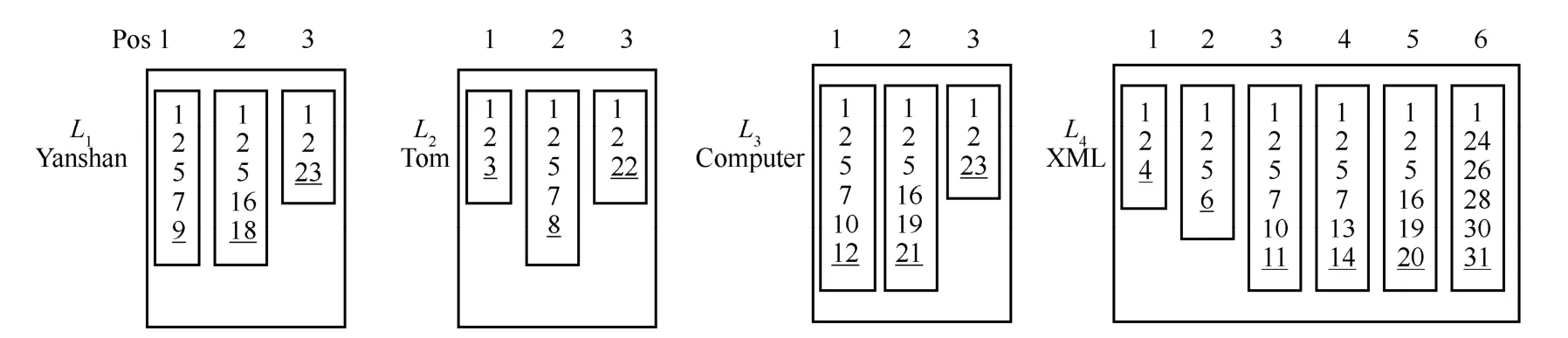
图4 查询关键字“Yanshan”(L1)，“Tom”(L2)，“Computer”(L3)，“XML”(L4)的倒排表

给定LCA节点v，若去掉以v的后代LCA节点为根的子树后，以v为根的子树仍然包含所有的关键字，则称v为ELCA节点。其形式化定义为ELCASet=ELCA(Q)={v|∃v1∈L1,…,vm∈Lm(v=lca(v1,v2,…,vm)∧∀i∈[1,m],，其中child(v,vi)指从节点v到节点vi路径上v的孩子节点。例如图3中满足Q={Yanshan,Tom,Computer,XML}的ELCA节点为2和7。

给定节点u和v，若u和v具有祖先后代关系，则函数desc(u,v)返回二者中的后代节点；若任一节点为空，则返回非空节点；若二者均空，则返回空值。假设S是有序节点集（按文档顺序升序有序），则lm(u，S)(rm(u，S))返回S中比u小（大）的最大（小）节点；若不存在满足条件的节点，则返回空值。

2.3 相关工作

现有方法构建的结果子树主要分为3类：1）受限结果子树[12]；2）完全子树[2,8]；3）路径子树[15]。其中完全子树指以满足特定语义节点v为根且未经修剪的原始子树；路径子树是指以v为根且由v到全部关键字节点的路径组成的子树；受限子树是指以v为根且满足相关特殊删减条件的子树。目前研究较多集中于受限结果子树，代表性的算法有MaxMatch[12]、MergeMatching[14]以及 RTF[13]。

MaxMatch与MergeMatching算法只针对SLCA语义求解相关关键字节点并构建结果子树，不能适用于ELCA语义。RTF算法虽然基于ELCA语义，但是不能正确求解相关关键字节点，导致其结果子树可能包含无用信息或者丢失有用信息。本文所提算法既能适用于 SLCA语义也能适用于 ELCA语义，并且能够正确、高效求解相关关键字节点。

3 RKN及其性质

针对已有方法[13]不能正确求解基于 ELCA语义的相关关键字节点集问题，为了进一步规范相关关键字节点，本文提出了相关关键字节点的形式化定义。

定义1 相关关键字节点：对于给定的查询Q，假设v为Q的ELCA节点，若关键字节点u满足以下条件：1)u不是LCA节点且u是v的后代节点；2)v到u的路径上不存在其他LCA节点，则称u为v的相关关键字节点。v的所有相关关键字节点组成的集合称为v的相关关键字节点集(RKNS,relevant keyword node set)Rv。

例如，给定图3中查询Q，ELCASet={2,7}。依据定义1，节点4为节点2的包含关键字“XML”的后代节点，且从2到4的路径上不存在LCA节点，故4是2的RKN。虽然节点6也为节点2的包含关键字“XML”的后代节点，但是从2到6的路径上存在LCA节点5，根据定义1，节点6不是节点2的RKN。以此类推，节点2的RKNS为R2={3,4,22,23}，节点7的RKNS为R7={8,9,11,12,14}。

依据 RKN的定义可知，若要判断一个节点 u是否为节点v的RKN，则必须保证从v到u的路径上不存在LCA节点。针对这个重要的条件，提出了最近LCA(CLCA，closest LCA)的概念。

定义2 最近 LCA：给定关键字节点 u，ul=lm(u，ELCASet)(ur=rm(u，ELCASet))表示节点u在ELCASet中的左(右)匹配节点，为u与ul(ur)的 LCA节点，则 u的 CLCA节点 c定义为c=

直观上看，节点u的CLCA节点c是给定查询Q的LCA节点，且从c到u的路径上不存在其他LCA节点，即c为距离u最近的祖先LCA节点。以图3中查询Q为例，ELCASet=｛2，7｝，关键字节点6在ELCASet中的左匹配为节点2，右匹配为节点7，其为2，为5，故其CLCA节点为5。同理，关键字节点18在ELCASet中的左匹配为节点7，右匹配为空，其为5，为空，故其CLC A节点为5。基于定义2，用定理1来判断给定关键字节点是否为某个ELCA节点的RKN。

定理1 设c为给定关键字节点u的CLCA节点，若c为ELCA节点，则u是c的RKN。

例如，关键字节点6的CLCA为5，但5不是ELCA节点，故6不是任一ELCA节点的RKN。又如，节点11的CLCA节点为7，且7是ELCA节点，故11是7的RKN。

4 RKN-Base算法

4.1 RKNS的表示

对于给定的查询Q={k1,k2,…,km}，通常用集合Rv={u1,u2,…,un}表示并存储节点v的全部RKN节点编码。显然，RKN节点编码已经存在于倒排表中，采用Rv={u1,u2,…,un}表示并存储会产生节点编码重复存储问题，造成内存空间的极大浪费。由于 v的 RKNS中许多节点都是连续分布在倒排表上，因此将v的RKN节点通过其在倒排表Li中的下标位置表示：RvLi={[s1,e1],… [sj,ej]}(j≤n)，其中，s表示一组连续RKN节点在倒排表上的起始位置，e表示一组连续RKN节点在倒排表上的结束位置。

例如R7L4={[3,4]}，ELCA节点7在L4(如图4所示)上第一个RKN的位置为3，最后一个RKN的位置为4。即通过[3,4]可知节点7的RKN的编码是1,2,5,7,10,11和1,2,5,7,13,14。

4.2 算法描述

假设每个倒排表Li都有一个关联的指针Ci，Ci指向Li中的某个节点。后续描述中，在不引起歧义的情况下，Ci可用于指代其所指节点。函数advance(Ci)的作用是让Ci指向下一个节点。

算法1 getRKNS-B(ELCASet)

算法1中，第1行对ELCASet中所有节点按照文档顺序排序。假设查询Q有m个关键字，在每次的循环过程中（第2）～7）行），算法1先从C1到Cm中选择最小节点Ci（第3）行），然后在第4）行得到Ci的CLCA节点c，如果c是ELCA节点，那么根据定理1，Ci是c的RKN，更新Rc. Li（第5）行）。第6行让Ci指向下一个节点。

例1 给定图 3中查询 Q=｛Yanshan,Tom,Computer,XML｝，ELCASet={2,7}，根据算法1，由图4倒排表可知其关键字节点处理顺序为：3,4,6,8,9,11,12,14,18,20,21,22,23,31。首先处理节点3，其CLCA节点为2，因为2为ELCA节点，则节点3是2的RKN，于是得到R2L2={[1,1]}(1,2,3节点属于L2)。其次，处理节点4，其CLCA节点为2，则节点4是2的RKN，于是有R2L4={[1,1]}。再次，处理节点6，其CLCA节点为5，由于5不是ELCA节点，故节点6不是任一ELCA节点的RKN，直接略过。后续的处理过程与前述相似，在处理完14个关键字节点后，ELCA节点2的RKNS为：R2L1={[3,3]}，R2L2={[1,1]，[3,3]}，R2L3={[3,3]}，R2L4={[1,1]}; ELCA节点 7的 RKNS 为:R7L1={[1,1]}，R7L2={[2,2]}，R7L3={[1,1]}，R7L4={[3,4]}。

4.3 算法分析

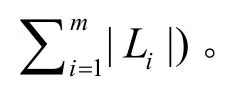
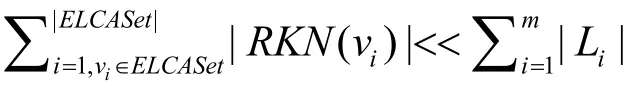
5 RKN-Optimized算法

5.1 主要思想

不同于算法 1遍历处理倒排表上的每一个节点，本文设计了一种优化算法，通过遍历处理每一个ELCA节点，利用ELCA节点去相应的倒排表查找其RKNS来提高算法效率。算法的主要思想为：对于每一个ELCA节点v，首先计算其后代节点在每个倒排表上的区间范围，用vLi=[s,e ]表示。其次寻找v的每个后代LCA节点u，并计算u的后代节点在每个倒排表上的区间范围，以u.Li=[s,e]表示。最后，依据RKN定义，vLi减去uLi即为节点v在第i个倒排表上RKNS的区间范围。

5.2 算法描述

算法 2采用栈 S存储每个 ELCA节点的IDDewey编码中的数字，这更加容易发现ELCA后代节点中的LCA节点。如图5(a)所示，当栈中存储节点1,2,5,7的编码时，节点5即为ELCA节点2的后代LCA节点。算法2首先将所有ELCA节点按文档顺序排序（第1)行），然后依次处理每一个ELCA节点（第2)～26)行）。具体来说，对于待入栈的ELCA节点v，将栈S中不是v祖先的节点全部出栈（第3)～6)行），对于每一个出栈的节点u，若u是ELCA节点，则直接得到其RKNS（第5)行）。然后，将v尚未入栈的祖先节点依次入栈（第 7)～25)行）。入栈过程中，对于v的每个祖先节点u(u≠v)，则首先将u标记为非ELCA节点（第9)行），然后检测当前栈顶元素top(S)是否为ELCA节点，如果top(S)是ELCA节点（第10)行将返回TRUE），则在第11)行调用locateRange得到u的后代节点在各个倒排表中的范围uLi，在第13)行将uLi从top(S)Li中去除。当v的所有祖先节点入栈后，在第17)～22)行处理v。如果top(S)为ELCA（第17)行），则将u标记为ELCA节点（算法 2第 17)～22)行 u=v），然后调用locateRange求出节点u的后代节点在各个倒排表中的范围uLi（第18)行），然后将u的RKNS从top(S)的RKNS中移除（第19)～21)行）。在24)行将u入栈。最后，在处理完所有的ELCA节点后，将栈中剩余节点全部出栈，求出栈中ELCA节点相应的RKNS（27)～30)行）。

算法2 getRKNS-O(ELCASet)

例 2 给定图 3中查询 Q=｛Yanshan,Tom,Computer,XML｝及其ELCASet={2,7}，算法2首先处理节点 2，将编码 1.2直接入栈并初始化，如图5(b)所示。其次处理节点7，因为栈顶节点2为ELCA节点，5为LCA节点，故需求出节点5的后代节点在倒排表中的范围并将节点5入栈。入栈的同时，将栈顶节点2的后代范围减去节点5的后代节点范围，如图5(c)所示。然后将节点7入栈，求出其后代节点范围。由于此时ELCASet中再无其他节点，故ELCA节点处理完毕，如图5(d)所示。最后将栈中节点全部出栈，最终得到ELCA节点2和7的RKNS。

5.3 算法分析

直观上看，算法2依次处理ELCASet中每一个ELCA节点，从而得到其RKNS。由于每一个ELCA节点最多调用2次locateRange函数，而locateRange函数的代价为O(d m log|Lm|)，因此算法 2的时间复杂度为O(| E LCASet| d m log|Lm|)。显然，和算法1相比，算法2可以避免处理无用节点。

由于不同SLCA节点之间没有祖先后代关系，其 RKN集合的求解非常简单，只需要顺序访问每个SLCA节点，在倒排表上调用locateRange函数，即可求出该SLCA节点的RKN区间范围，具体过程不再赘述。

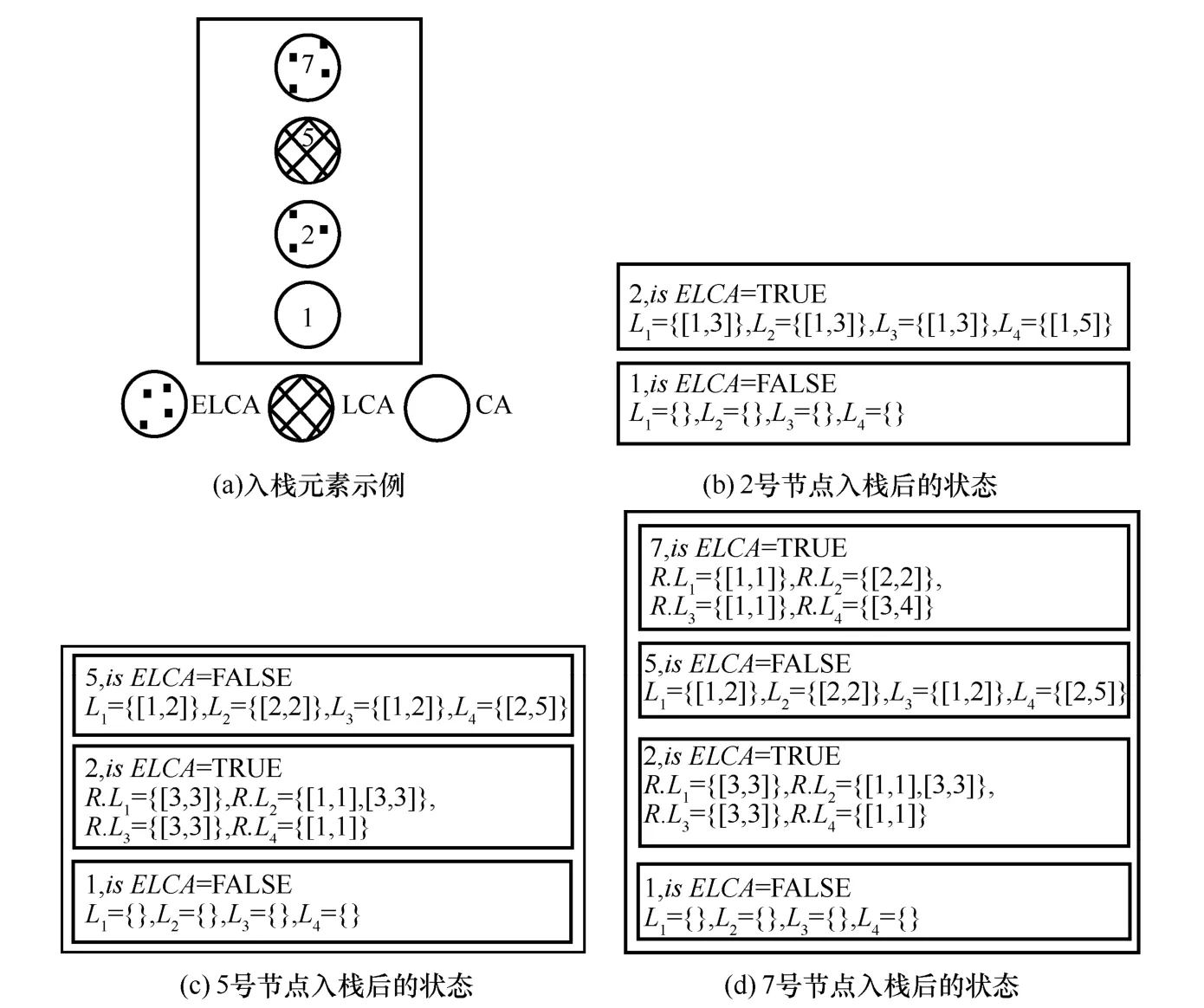
图5 例2的运行图

6 实验

6.1 实验环境

本文实验所用机器的基本配置为AMD AthonⅡX2270 Professor 3.4 GHz CPU，2 GB内存，500 GB硬盘，操作系统为Windows XP。

为了进行公平比较，只比较基于内存数据的算法性能。实验所采用的数据集为XMark (582 MB)与DBLP注3http://www.informatik.uni-trier.de/～ley/db/。(876 MB)。在解析 2个数据集之后，基于Oracle Berkeley DB4，使用一个散列文件来存储所有的关键字倒排表，其中散列文件的每个key是一个关键字k，value是k对应的存储Dewey编码的倒排表。当处理给定查询Q时，Q对应的倒排表首先被读入到内存，所有实验结果均不考虑I/O代价的影响。

从 XMark数据集中选取了一组关键字，这些关键字根据其在数据集中出现的次数分为3类：1)低频关键字(100～1000); 2)中频关键字(10000～40000);3)高频关键字(300000～600000)。基于这些关键字，生成了 12个查询，按照关键字个数分成 4组(Group1：2个关键字；Group2：3个关键字；Group3：4个关键字；Group4：5个关键字)，如表1所示。表示所有关键字倒排表的长度之和，|Lmax|(|Lmin|)表示最长(最短)倒排表的长度，NE表示满足条件的ELCA节点个数，RE=NE/|Lmin|表示结果选择率。DBLP数据集上的查询也用类似的方式生成，由于XMark数据集包含较复杂的文档结构，且数据集大小可以按比例调整以便进行扩展性测试，本文中主要展示基于XMark数据集的实验结果。所有算法均用Visual C++ 语言实现，运行时间为算法执行100次的平均值。

6.2 性能比较和分析

表2为12个查询的运行时间比较，其中，TB表示RKN-Base运行时间，TO表示RKN-Optimized运行时间，Re=TO/TB表示2个算法运行时间的比率，由实验结果可知。

1)对RKN-Base而言，由于其需要处理所有的关键字节点(表1第3列，因此当关键字节点个数较多时，性能较差，例如Q10。同时，其性能也受ELCA节点个数(表1第6列NE)的影响，当ELCA节点个数变多时，所需时间明显增大，这是由其时间复杂度中的log|ELCASet|决定的，例如Q2和Q3。

2)对RKN-Optimized而言，由于其循环次数由ELCA节点个数决定，因此当ELCA节点个数较少时，性能较好，如 Q1，Q4，Q7，Q8，Q9，Q10，Q11等，甚至在某些情况下优于RKN-Base 4个数量级，例如Q1，Q4，Q7，Q10。随着结果选择率的增加，RKN-Optimized的性能优势逐渐下降，个别情况下甚至比RKN-Base差，这是因为RKN-Optimized需要处理大量的ELCA节点，例如Q3。

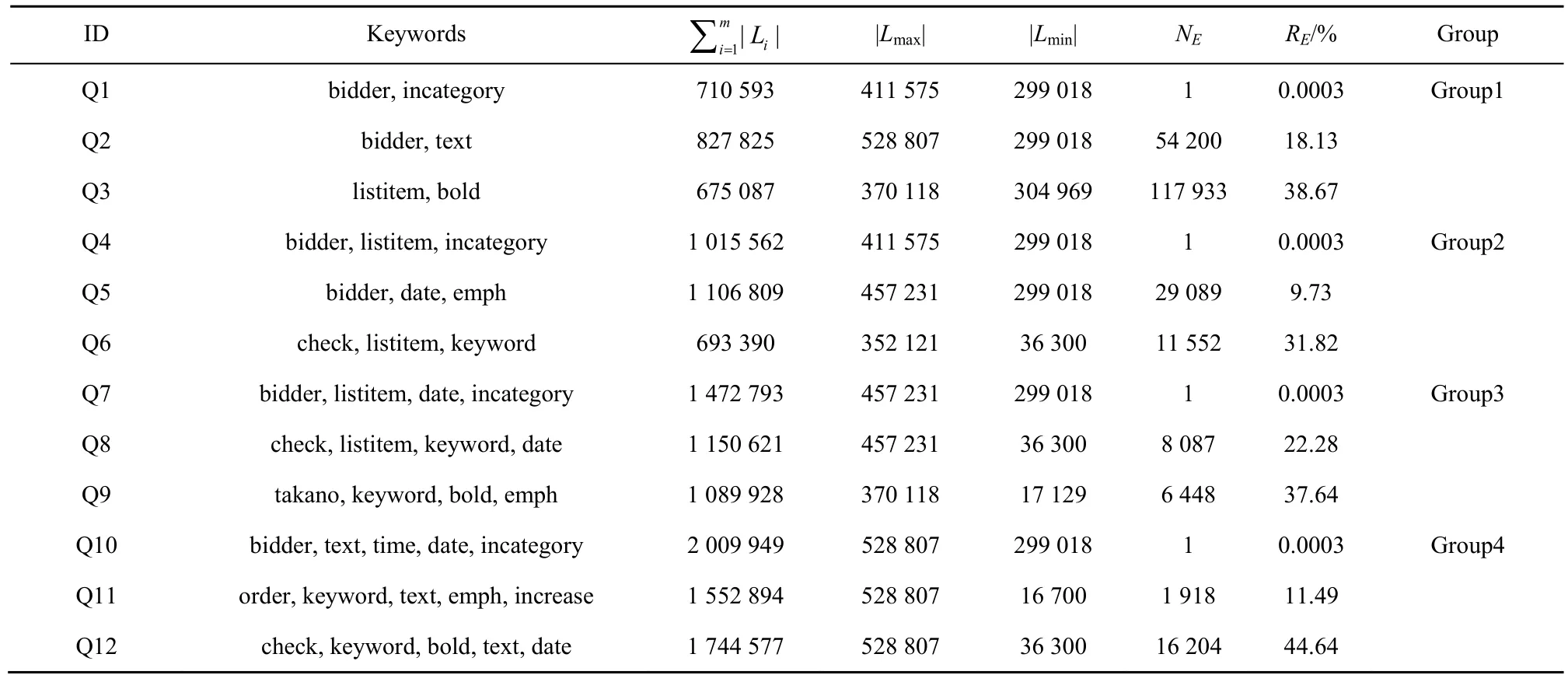
表1 基于XMark数据集的查询

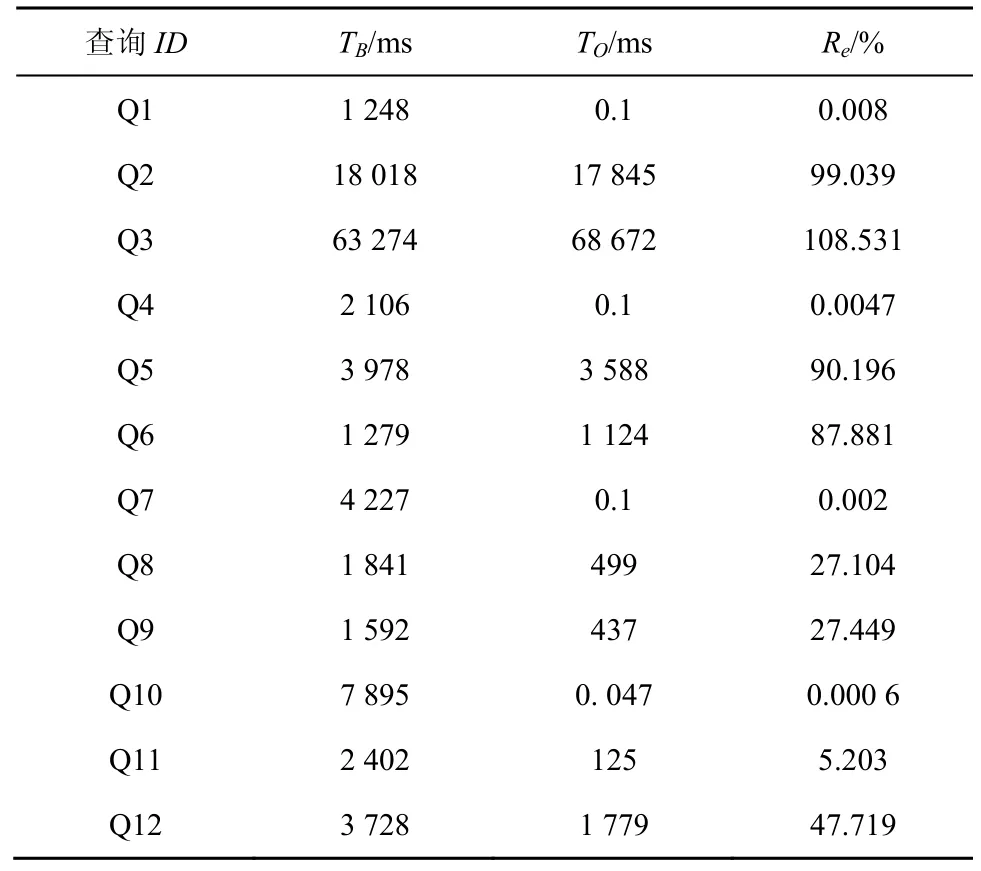
表2 RKN-Base与RKN-Optimized运行12个查询的运行时间

以上观察及表2的实验结果可进一步由表3的数据来解释。表3为2种算法中执行基本操作(编码比较操作)的次数，该数据可以客观反映不同算法运行时间的差异。其中，NB表示RKN-Base编码比较次数，NO表示RKN- Optimized编码比较次数，Re=NO/NB表示2个算法编码比较次数的比率，如表 3所示，对Q1，Q4，Q7，Q10而言，RKN-Optimized的编码比较次数远少于RKN-Base，因此其所需运行时间远小于 RKN-Base。对 Q3而言，RKNOptimized的编码比较次数接近RKN-Base，因此其所需运行时间与RKN-Base也相差不大。

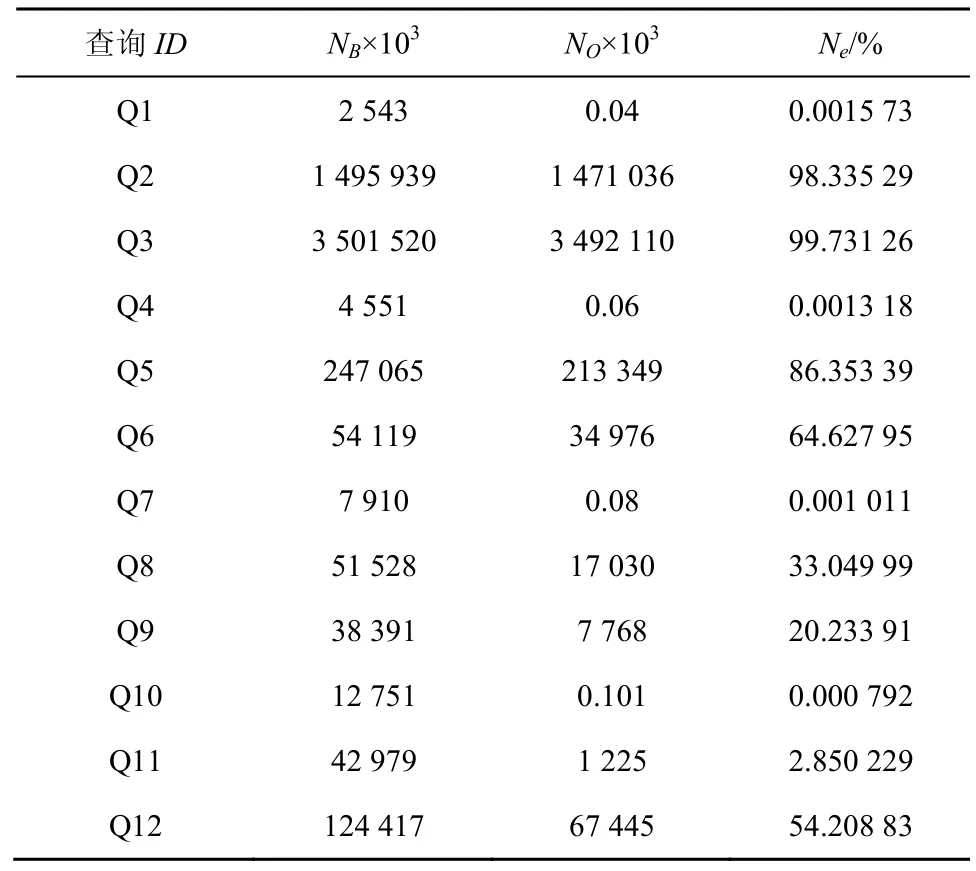
表3 RKN-Base与RKN-Optimized运行12个查询的编码比较次数

除了表1的12个查询，本文还随机生成了17万查询，算法运行时间按照查询关键字个数及结果选择率分类，如图6所示。该实验结果进一步验证了：1)关键字个数较少，结果选择率较高时，RKN-Optimized性能最差。例如图 6(a)中结果选择率为[40,100]时，RKN-Optimized与RKN-Base运行时间基本相同。2)关键字个数较多，结果选择率较低时，RKN-Optimized性能最好。如图 6(d)中结果选择率为(0,1)时，RKN-Optimized运行时间优于RKN-Base近100倍。3)考虑单个因素时，随着关键字个数的增加，RKN-Optimized性能优势逐渐上升。例如图6中随着关键字个数增加，图6(c)和图6(d)中RKN-Optimized的整体性能优于图6(a)和图6(b)。另外，随着结果选择率的升高，RKN-Optimized的优势逐渐下降。

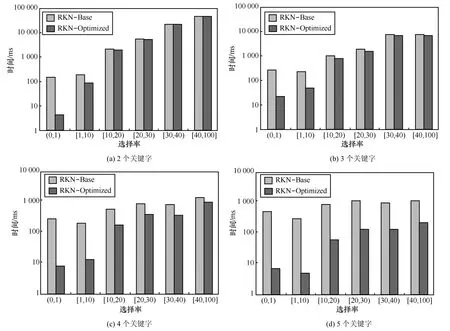
图6 运行时间比较

图7给出在不同大小的XML文档上执行查询Q8的运行时间。从图中可以看出本文方法有非常好的扩展性，对于其他的查询，有类似的结果，因此不再赘述。

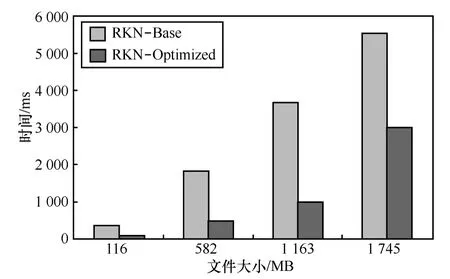
图7 Q8在不同大小XML文档上的运行时间

表4为DBLP数据集上的10个查询，其中，NE为ELCA个数，算法运行时间如图8所示。通过实验可知，RKN-Optimized在大多数情况下优于RKN-Base，原因同样是因为RKN-Optimized避免了处理大量无用节点。

表4 基于DBLP数据集的查询

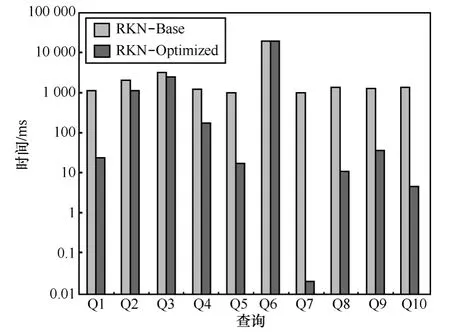
图8 DBLP数据集上运行时间

7 结束语

构建结果子树是XML关键字查询处理的核心问题，其中求解与每个子树根节点相关的关键字节点集是影响结果子树构建效率的重要步骤。针对已有方法不能正确求解基于ELCA语义的相关关键字节点集的问题，本文提出了相关关键字节点的形式化定义RKN。依据该定义提出了基本算法RKN-Base，该算法通过顺序扫描每个关键字节点一次即可判断其是否为某个ELCA节点的相关关键字节点。针对RKN-Base算法不能避免处理无用节点的问题，提出了优化算法RKN- Optimized。该算法基于每个ELCA节点求其相关关键字节点，可避免处理无用关键字节点，降低时间复杂度。最后通过实验对所提算法的性能进行了验证和分析。

本文的后续工作将针对生成结果子树的第3步（构建结果子树）展开研究，进而设计并实现一个完整、高效的XML关键字查询处理系统。

[1]TATARINOV I,VIGLAS S,BEYER K S,et al. Storing and querying ordered XML using a relational database system[A]. SIGMOD Conference[C]. 2002. 204-215.

[2]GUO L,SHAO F,BOTEV C,et al. Xrank: ranked keyword search over XML documents[A]. SIGMOD Conference[C]. 2003.16-27.

[3]ZHOU RUI,LIU CHENGFEI,LI JIANXIN. Fast elca computation for keyword queries on XML data[A]. International Conference on Extending DB Technology[C]. Lausanne,Switzerland,2010.549-560.

[4]COHEN S,MAMOU J,KANZA Y,et al. Xsearch: a semantic search engine for XML[A]. VLDB[C]. 2010. 45-56.

[5]LI G,FENG J,WANG J,et al. Effective keyword search for valuable lcas over XML documents[A]. CIKM[C]. 2007.31-40

[6]ZHOU J,BAO Z,CHEN Z,et al. Top-down SLCA computation based on list partition[A]. DASFAA[C]. 2012.

[7]WANG W Y,WANG X L,ZHOU A Y. Hash-search: an efficient slca-based keyword search algorithm on XML documents[A]. LNCS 5463[C]. 2009. 496-510.

[8]XU Y,PAPAKONSTANTINOU Y. Efficient keyword search for smallest lcas in XML databases[A]. SIGMOD Conference[C]. 2005.

[9]SUN C,CHAN C Y,GOENKA A K. Multiway slca-based keyword search in XML data[A]. WWW[C]. 2007.1043-1052.

[10]ZHOU J,BAO Z,WANG W,et al. Fast SLCA and ELCA computation for XML keyword queries based on set intersection[A]. ICDE[C].2012.

[11]XU Y,PAPAKONSTANTINOU Y. Efficient lca based keyword search in XML data[A]. EDBT[C]. 2008.

[12]LIU Z,CHEN Y Reasoning and identifying relevant matches for XML keyword search[J]. PVLDB,2008. 1(1): 921-932.

[13]KONG L,GILLERON R,LEMAY A. Retrieving meaningful relaxed tightest fragments for XML keyword search[A]. EDBT[C]. 2009.815-826.

[14]ZHOU J,BAO Z,CHEN Z,et al. Fast result enumeration for keyword queries on XML data[A]. DASFAA[C].2012.95-109.

[15]HRISTIDIS V,KOUDAS N,PAPAKONSTANTINOU Y,et al. Keyword proximity search in XML trees[J]. IEEE Trans Knowl Data Eng,2006,18(4):525-539.

[16]TATARINOV I,VIGLAS S,et al. Storing and querying ordered XML using a relational database system[A]. Special Interest Group on Management of Data Conference[C]. Madison,USA,2002. 204-215.

[17]BRODER A Z. A taxonomy of Web search[J]. SIGIR Forum,2002,36(2):3-10.