应用Legendre小波求解非线性分数阶Volterra积分微分方程
2014-10-25韩惠丽
黄 洁,韩惠丽
(宁夏大学 数学计算机学院,银川750021)
分数阶微积分及其方程广泛应用于力学和种群问题等领域中.分数阶积分(微分)方程的解析解求解较困难,且方法少.目前,分数阶积分(微分)方程的数值解法主要有同伦摄取法[1]、Taylor展式法[2]、Adomin分解法[3]和小波基方法[4-10]等.由于小波基的正交性使化简后代数方程组的矩阵是稀疏的,因此小波方法广泛应用于数值求解积分方程和偏微分方程问题中.文献[5-6]分别采用CAS小波的分数阶积分算子矩阵和第二类Chebyshev小波(SCW)的分数阶积分算子矩阵研究了非线性分数阶Volterra积分微分方程的数值解问题,得到了相应的结果.本文利用Legendre小波求解非线性分数阶Volterra积分微分方程.与文献[5-6]相比,相同点是将非线性分数阶Volterra积分微分方程转化为非线性代数方程组求解,不同点是本文通过Legendre小波和分数阶微积分的概念推出了Legendre小波的分数阶积分算子矩阵,并证明了这种方法的误差边界值.
考虑如下形式的第二类非线性分数阶Volterra积分微分方程:

满足初始条件

其中:f(x),k(x,t)∈L2([0,1])为已知函数;Dα为Caputo分数阶微分算子;y(x)为未知函数;q为正整数.
1 Legendre小波
定义1[11]在[0,1)上定义Legendre小波如下:

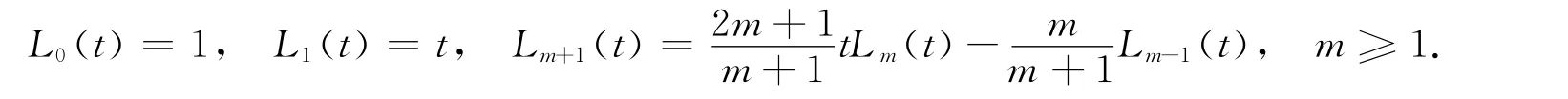
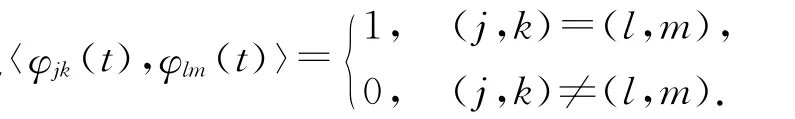

对于定义在[0,1)上的函数f(t)可用Legendre小波展开为
式中:
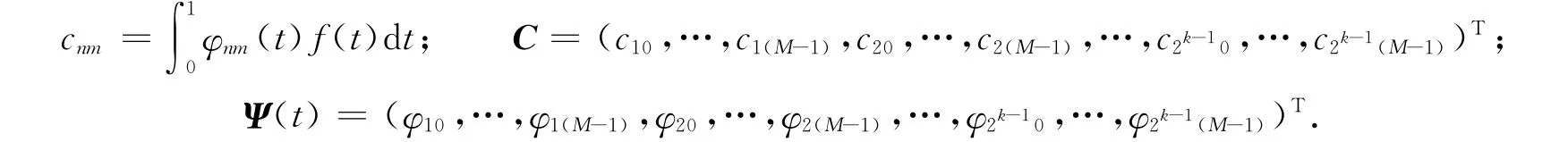


当M=3,k=2时,Legendre小波矩阵表示为

2 Legendre小波的分数阶积分算子矩阵
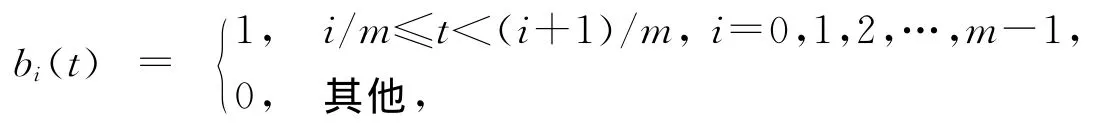
定义3[12]R-L 分数阶积分定义为
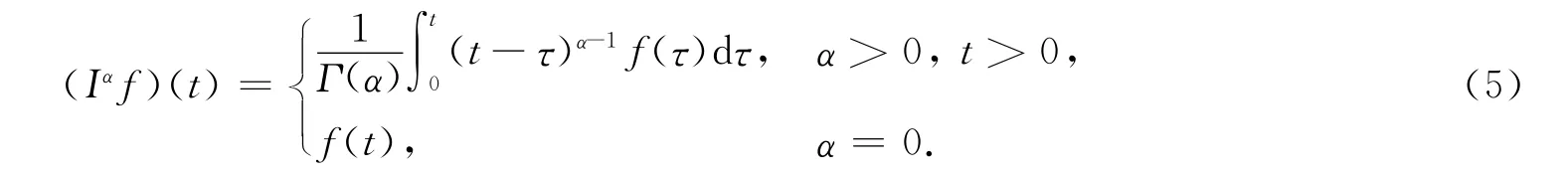
定义4[12]Caputo分数阶微分定义为

式(5)和式(6)有如下关系:

其中m-1<α≤m,m∈ℕ.
对于[0,1)上的平方可积函数f(t)可用BPFs展开为

式中:F=(f0,f1,…,fm-1)T;Bm(t)=(b0(t),b1(t),…,bm-1(t))T.
于是Legendre小波可由m′个块脉冲函数表示为

由BPFs的分数阶积分算子矩阵性质[13]得

式中

下面求解Legendre小波的分数阶积分算子矩阵.设

则Pα称为Legendre小波的分数阶积分算子矩阵.由式(10),(11)可得

再由式(12),(13)得

3 方程的转化
将式(1)中的函数Dαy(x)和f(x)用Legendre小波展开为

其中K 是 m′×m′矩 阵,其 元 素 为kij= 〈φnm(x),〈k(x,t),φm′n′(t)〉〉,i= (n-1)M +m+1,j=(n′-1)M+m′+1.
由式(8),(12),(15)计算得

令A=(a0,a1,…,am′-1)=(YTPα+)Φm′×m′,则y(x)≈ABm′(x),(y(x))q≈AqBm′(x),其中由数学归纳法得


将式(15)~(18)代入式(1)得
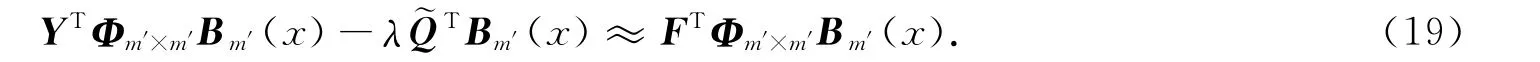

通过数值求解方程组(20),可得式(1)的近似解.
4 误差分析

随着q的不断增大,Cq以指数形式不断减小.由于截断Legendre小波的系数即为方程的近似解,所以定义2-范数的误差函数为

其中:y(x)为精确解;ym′(x)为式(20)得到的数值解.


证明:设S=YTPα+,且


又因为rq(x)为y(x)在区间In上的q次插值多项式,所以

因此,由式(22)得

5 数值算例
例1 求解满足初始条件y(0)=0的积分微分方程:

令M=2,k=6,取α分别为1,0.9,0.8进行数值求解,并与文献[15]中采用HPM方法得到的结果进行比较,结果列于表1.由表1可见,当α=1时,本文方法的数值解一致逼近精确解.
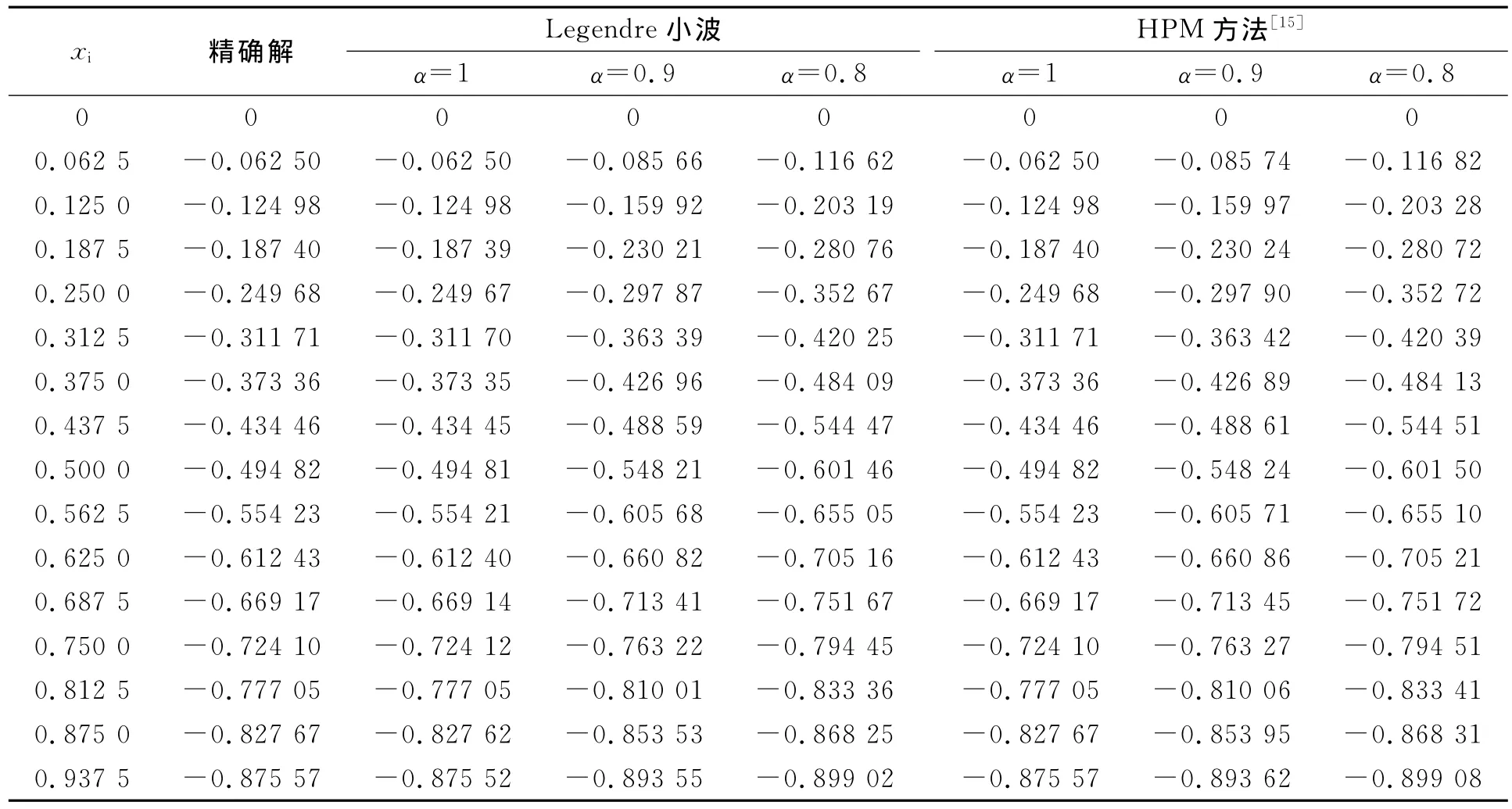
表1 Legendre小波与HPM方法的数值解对比Table 1 Contrast of numerical results by Legendre wavelet and HPM method
例2 解满足条件y(0)=y′(0)=0的积分微分方程:

其精确解为y(x)=x2.令M=1,k分别取4,5,6,7时,2-范数误差的近似值列于表2.其精确解与数值解如图1所示.由表2和图1可见:随着节点的不断增多,数值解的精度逐渐提高,误差越来越小.

图1 当M=1,k=4,5,6,7时数值解与精确解的比较Fig.1 Comparison between numerical solution and exact solution for M=1and k=4,5,6,7
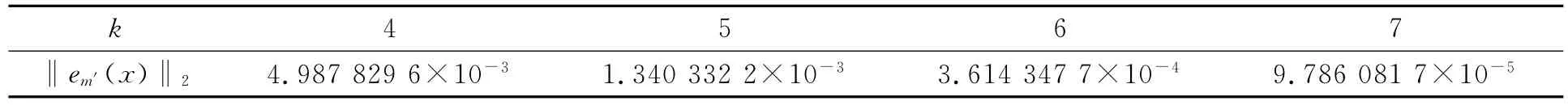
表2 当M=1时不同k值2-范数误差的近似值Table 2 Approximate values of absolute errors for norm-2at different kof the Legendre wavelet when M=1
综上可见,本文采用Legendre小波求解了非线性第二类分数阶Volterra积分微分方程,先将方程转化为非线性方程组进行数值求解,再通过矩阵的稀疏化简化了运算量.误差分析和数值算例结果表明,采用Legendre小波运算可行、有效.
[1]Nawaz Y.Variational Iteration Method and Homotopy Perturbation Method for Fourth-Order Fractional Integro-Differential Equations[J].Comput Math Appl,2011,61(8):2330-2341.
[2]HUANG Li,LI Xianfang,ZHAO Yulin,et al.Approximate Solution of Fractional Integro-Differential Equations by Taylor Expansion Method[J].Comput Math Appl,2011,62(3):1127-1134.
[3]Momani S,Noor M A.Numerical Methods for Fourth-Order Fractional Integro-Differential Equations[J].Appl Math Comput,2006,182(1):754-760.
[4]Saeedi H,Mohseni Moghadam M,Mollahasani N,et al.A CAS Wavelet Method for Solving Nonlinear Fredholm Integro-Differential Equations of Fractional Order[J].Commun Nonlinear Sci Numer Simulat,2011,16(3):1154-1163.
[5]Saeedi H,Mohseni Moghadam M.Numerical Solution of Nonlinear Volterra Integro-Differential Equations of Arbitrary Order by CAS Wavelets[J].Commun Nonlinear Sci Numer Simulat,2011,16(3):1216-1226.
[6]ZHU Li,FAN Qibin.Numerical Solution of Nonlinear Fractional-Order Volterra Integro-Differential Equations by SCW [J].Commun Nonlinear Sci Numer Simulat,2013,18(5):1203-1213.
[7]ZHU Li,FAN Qibin.Solving Fractional Nonlinear Fredholm Integro-Differential Equations by the Second Kind Chebyshev Wavelet[J].Commun Nonlinear Sci Numer Simulat,2012,17(6):2333-2341.
[8]仪明旭,陈一鸣,魏金侠,等.应用Haar小波求解非线性分数阶Fredholm积分微分方程 [J].河北师范大学学报:自然科学版,2012,36(5):452-455.(YI Mingxu,CHEN Yiming,WEI Jinxia,et al.Haar Wavelet Method for Solving Nonlinear Fredholm Integro-Differential Equations of Fractional Order[J].Journal of Hebei Normal University:Natural Science Edition,2012,36(5):452-455.)
[9]LepikÜ.Haar Wavelet Method for Nonlinear Integro-Differential Equations[J].Appl Math Comput,2006,176(1):324-333.
[10]尹建华,任建娅,仪明旭.Legendre小波求解非线性分数阶Fredholm积分微分方程 [J].辽宁工程技术大学学报:自然科学版,2012,31(3):405-408.(YIN Jianhua,REN Jianya,YI Mingxu.Legendre Wavelet Method for Solving Nonlinear Fredholm Integro-Differential Equations of Fractional Order[J].Journal of Liaoning Technical University:Natural Science,2012,31(3):405-408.)
[11]Rehman M,Khan R A.The Legendre Wavelet Method for Solving Fractional Differential Equations[J].Commun Nonlinear Sci Numer Simulat,2011,16(11):4163-4173.
[12]Das S.Functional Fractional Calculus[M].2nd ed.Berlin:Springer-Verlag,2011.
[13]Kilicman A,Al Zhour Z A A.Kronecker Operational Matrices for Fractional Calculus and Some Applications[J].Appl Math Comput,2007,187(1):250-265.
[14]Biazar J,Ebrahimi H.Chebyshev Wavelets Approach for Nonlinear Systems of Volterraintegral Equations[J].Comput and Math Appl,2012,63(3):608-616.
[15]Ghazanfari B,Ghazanfari A G,Veisi F.Homotopy Perturbation Method for the Nonlinear Fractional Integro-Differential Equations[J].Aust J Basic Appl Sci,2010,4(12):5823-5829.
