量子系统中的SU(R)典型生成元
2014-10-25李嫦娥卜繁强陶元红
李嫦娥,卜繁强,陶元红
(1.延边大学 理学院数学系,吉林 延吉133002;2.延边大学 师范分院,吉林 延吉133002)
特殊酉群SU(R)在量子物理中应用广泛,如在粒子物理的标准模型中,群SU(2)应用于电弱相互作用中[1];群SU(3)应用于量子色动力学中[2-3].本文研究特殊酉群SU(R)典型生成元的性质,并给出了单粒子量子态密度矩阵的具体表示形式及其表示系数所满足的关系式.
1 预备知识
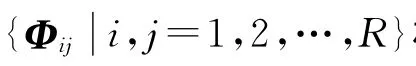
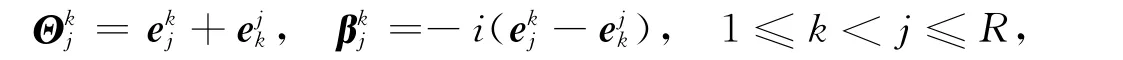
对角生成元有R-1个,形式如下:
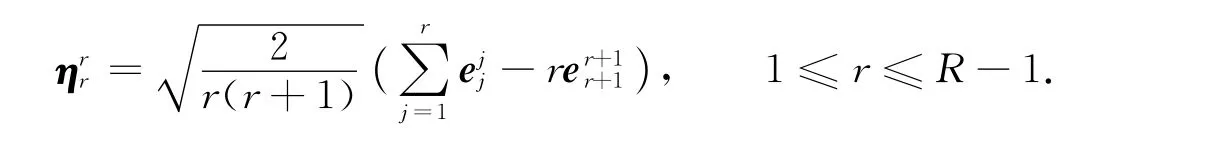
定义λ矩阵如下:

由此可得R2-1个迹为0的生成元{λi,i=1,2,…,R2-1},称该组生成元为SU(R)的典型生成元.
构造典型生成元的初等矩阵满足如下性质:
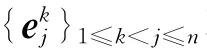
根据引理1,SU(R)的典型生成元满足如下性质:
引理2[6]设{λi,i=1,2,…,R2-1}为SU(R)的典型生成元,则tr(λi)=0,tr(λiλj)=2δij.
2 典型生成元的性质
定理1 设{λj,j=1,2,…,R2-1}为SU(R)的典型生成元,则如下等式成立:

证明:根据k,q,l,p的取值,下面分3种情形讨论.

① 若k=q=l=p=R,则有
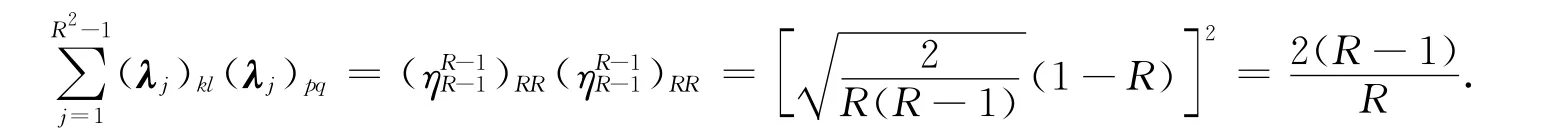
② 若k=q=l=p≠R,用归纳法证明式(1).当k=1时,显然有

设k=s时有
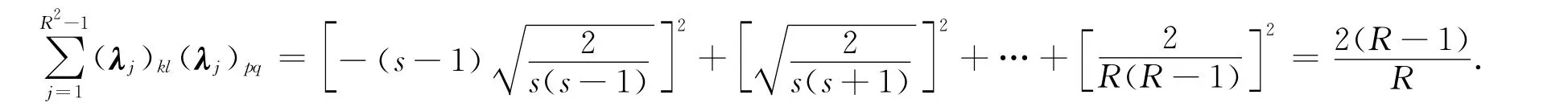
当k=s+1时,由于
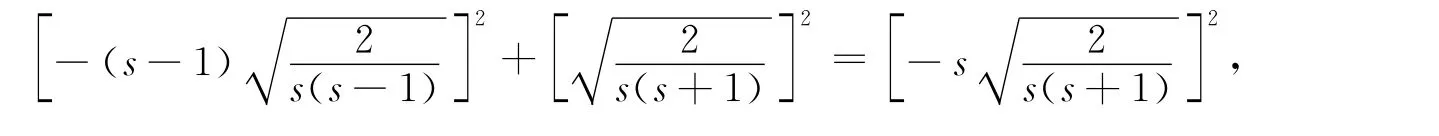
因此
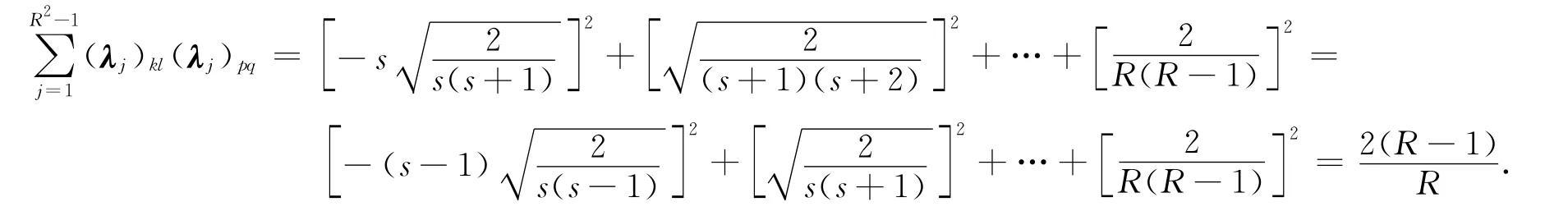
即式(1)成立,从而定理1结论成立.
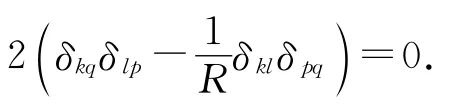
情形3)k,q,p,l两两相等且不全相等.此时,又分3种情形.
① 若k=q≠l=p,不妨设k=q>l=p.易证2(δkqδlp-R-1δklδpq)=2.于是,
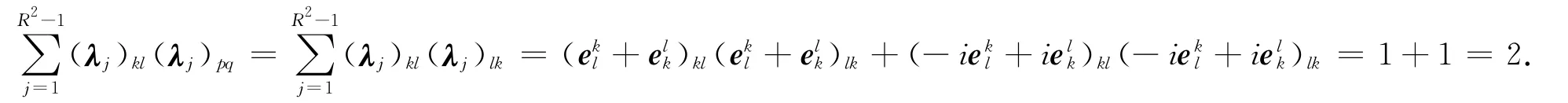
② 若k=p≠l=q,不妨设k=p>l=q,易证此时有2(δkqδlp-R-1δklδpq)=0.于是
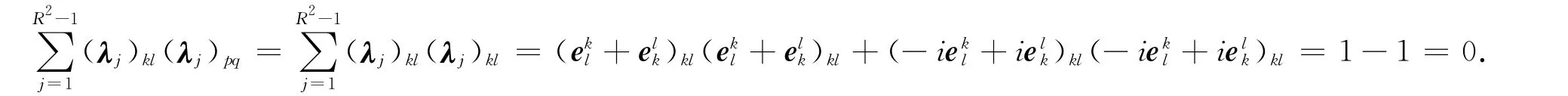
③ 若k=l≠q=p,不妨设k=l<q=p,易证此时有2(δkqδlp-R-1δklδpq)=-2/R.当k=l<q=p=R时,有
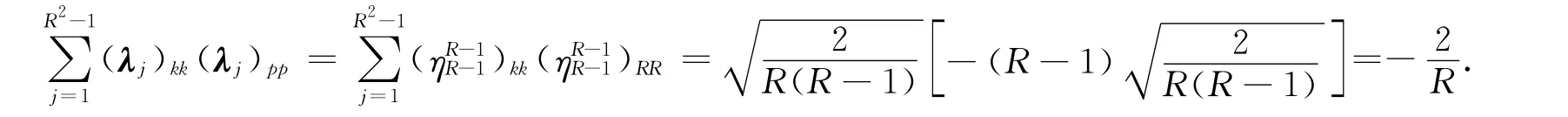
当k=l<q=p≠R时,有
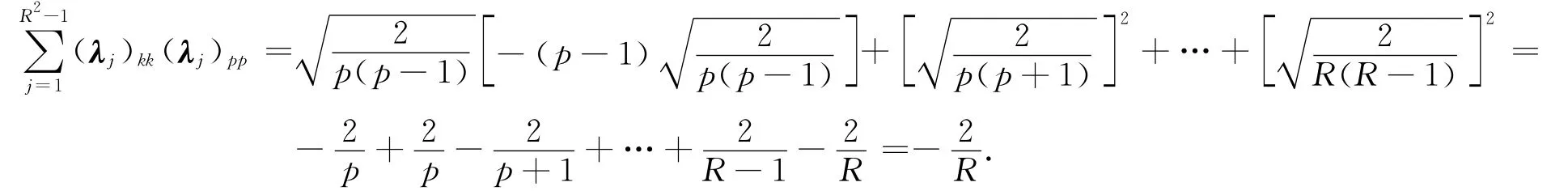
综上,定理1结论成立.
3 单粒子态密度矩阵的性质
R维Hilbert空间上任意一个Hermitian算子均可由单位算子I和特殊酉群SU(R)的生成元表示[5].由于R维系统的密度算子ρ是迹为1的半正定Hermitian算子,因此ρ可用单位算子和SU(R)生成元表示,即

其中:IR为R×R的单位矩阵;{λj:j=1,2,…,R2-1}为SU(R)的典型生成元;aj均为实数.若密度算子ρ满足tr(ρ2)=1,则称ρ为纯态[7];若tr(ρ2)<1,则称ρ为混合态[7].
式(2)系数满足的关系式可参见文献[8-9].本文利用定理1讨论单粒子态密度矩阵的形式及其系数满足的关系式.
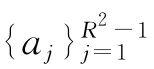

证明:1)由式(2)和引理1,可得
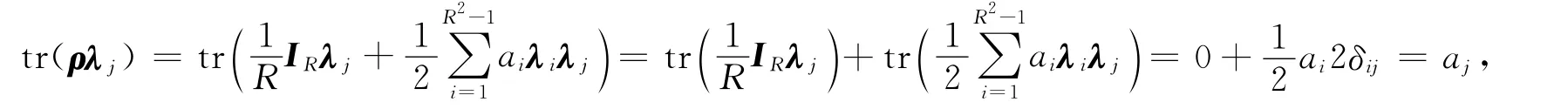
故式(3)成立.
2)先证

设ρ和λj的矩阵形式如下:
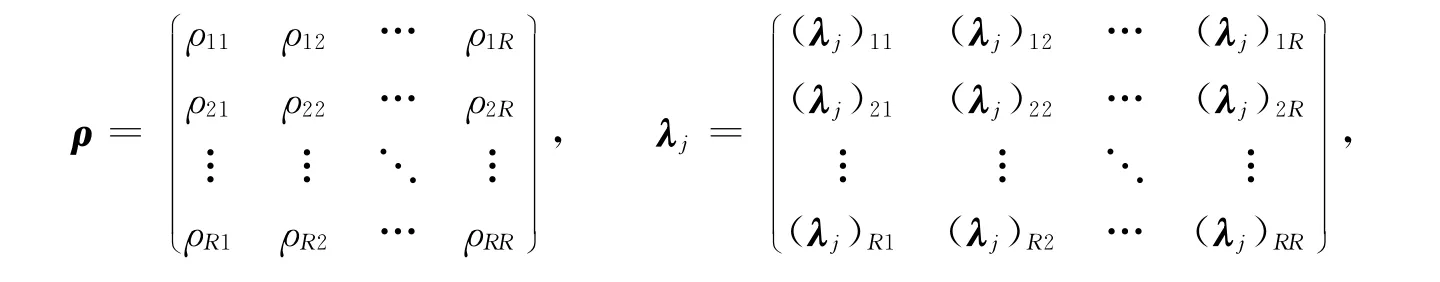
则矩阵ρλj表示如下:
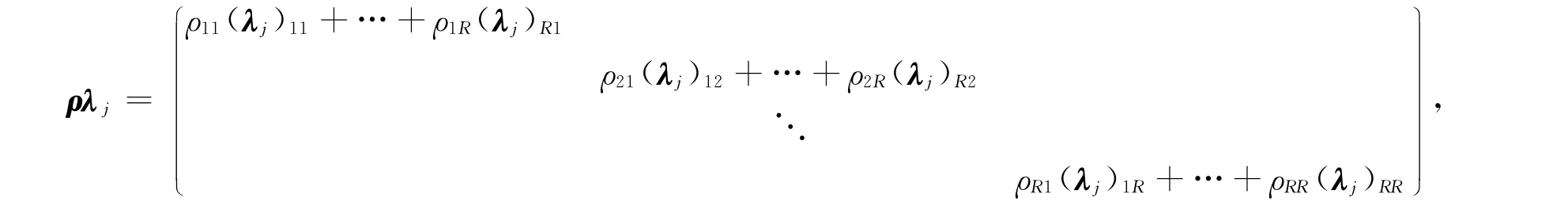
于是,

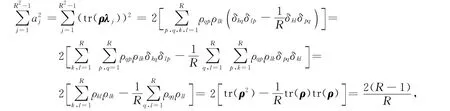
即式(4)成立,从而定理2成立.
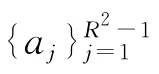
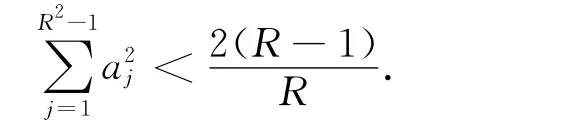
证明:由于混合态对应的密度矩阵ρ满足tr(ρ2)<1,因此类似定理2的证明过程即得结论.
[1]WEI Qun.Research of High Temperature Superconductors[J].Journal of Dezhou University,2003,19(2):32-34.(魏群.高温超导机制研究的现状与发展 [J].德州学院学报,2003,19(2):32-34.)
[2]ZHANG Wen-zhong,WANG Shun-jin.Algebraic Dynamical Solutions of SU(3)Linear Nonautonomous Quantum System [J].Acta Physica Sinica,1997,46(2):209-226.(张文忠,王顺金.SU(3)线性非自治量子系统的代数动力学求解 [J].物理学报,1997,46(2):209-226.)
[3]ZENG Bao-sheng,HUANG Qing,GONG Xue-hui.The Level Symmetry of Leptons and Quarks[J].Journal of Lanzhou University:Natural Sciences,1981(1):25-28.(曾保生,黄庆,宫学惠.轻子与夸克的水平对称性 [J].兰州大学学报:自然科学版,1981(1):25-28.)
[4]朱洪元.群论和量子力学中的对称性 [M].北京:北京大学出版社,2009.
[5]Thew R T,Nemoto K,White A G,et al.Qubit Quantum-States Tomography[J].Phys Rev A,2002,66(1):1-6.
[6]WANG Wei-wei,CAO Huai-xin.A Note on the Separability of Quantum Mixed States[J].Journal of Xianyang Normal University,2008,23(2):6-9.(汪威威,曹怀信.二元量子系统混态密度矩阵可分性研究 [J].咸阳师范学院学报,2008,23(2):6-9.)
[7]李承祖.量子通讯与量子计算 [M].长沙:国防科技大学出版社,2000.
[8]ZHAO Hui,WANG Zhi-xi.Separability Criteria for Quantum Mixed States[J].Common Theor Phys,2004,42(4):529-534.
[9]WANG Wei-wei,BI Hong-mei.Separability Criterion of Bipartite Qubit States [J].Journal of Xi’an Technological University,2008,28(5):414-416.(汪威威,毕红梅.两体量子态可分离性判据 [J].西安工业大学学报,2008,28(5):414-416.)
