环 的 强 正 则 性
2014-10-25殷晓斌陈赛男
殷晓斌,陈赛男,豆 皖
(安徽师范大学 数学计算机科学学院,安徽 芜湖241003)
0 引 言
本文的环均指有单位元的结合环,环上的模均指单式模.设R是环,J(R),C(R)和N(R)分别表示R的Jacobson根、中心和幂零元之集.对于R中的任意元a,l(a)和r(a)分别表示a的左零化子和右零化子.如果对于任意的a∈R,存在正整数n,使得an≠0,且任意左R-模同态f:Ran→M均可扩张为R到M 的同态,则左R-模M 称为左GP-内射模[1].类似可定义右GP-内射模.如果R的每个单左(右)R-模是GP-内射的,则R称为左(右)GP-V-环[1];如果环R的每个单奇异左(右)R-模是GP-内射的,则R称为左(右)GP-V′-环[1].如果R中不含非零的幂零元,则R称为约化环[1].如果对于任意的a∈R,存在b∈R,使得a=a2b,则R称为强正则环[2].强正则环具有左右对称性.如果对于R的任意左(右)理想I,均有I2=I,则R称为左(右)弱正则环[3].如果R的每个左理想是由幂等元生成的,则R称为广义正则环[4].如果对于任意的r∈R,x∈L,存在正整数n,使得(rx)n∈L(或(xr)n∈L),则环R的子加群L称为R 的弱左(右)理想[4].如果J(R)=N(R),则环R称为J-环[5].如果对于任意的a,b,r∈R,且ab=0,有arb∈C(R),则R称为中心半交换环.如果对于任意的a∈N(R),存在正整数n,使得an≠0,且任意左R-模同态f:Ran→M均可扩张为R到M 的同态,则左R-模M 称为左wnil-内射模[6].如果对于任意的a,b∈R,ab=0,存在正整数n,使得an≠0,bn≠0,anRbn=0,则R称为拟ZI-环[7].
1 GP-V-环与GP-V′-环的强正则性
引理1 设R是环,若R的每个主左(右)理想是弱右(左)理想,则R/J(R)约化.
证明:仅证左的情形,右的情形类似可证.
对任意的a∈R,若a∉J(R)且a2∈J(R),则存在R的极大左理想M,使得M+Ra=R.由a2∈J(R)可得R=M+Ma.于是存在m∈M,使得1-ma∈M.由于Rm是弱右理想,故存在正整数n,使得(ma)n∈Rm⊆M.因此有
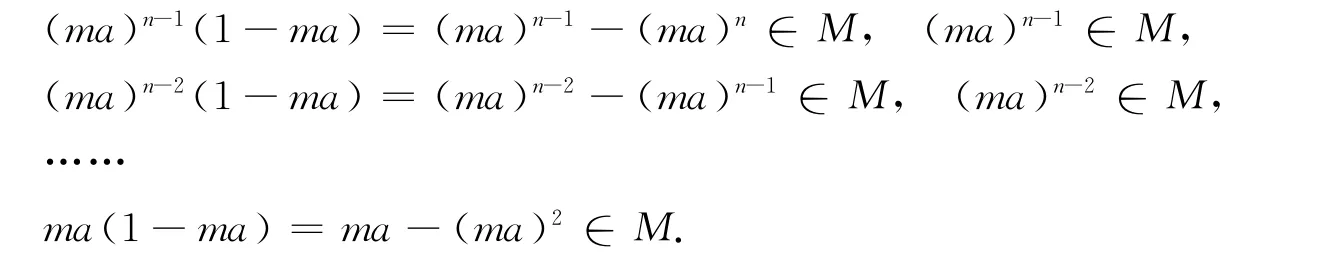
故ma∈M,1=ma+(1-ma)∈M,矛盾.所以a∈J(R),R/J(R)约化.证毕.
引理2[1]若环R 是左(右)GP-V-环,则J(R)=0.
引理3 设R是环,若R为每个幂等元是中心元的左(右)GP-V′-环,且每个主左(右)理想是弱右(左)理想,则R是约化环.
证明:仅证左的情形,右的情形类似可证.
对任意的a∈R,若a≠0且a2=0,则存在R的极大左理想M,使得l(a)⊆MR,因此可以定义左R-模同态f:Ra→R/M;rar+M,∀r∈R.
下证M是本质左理想.若不然,则存在e2=e∈R,使得M=Re=l(1-e).由a∈Ra⊆M=l(1-e)及R的每个幂等元是中心元知,a(1-e)=0=(1-e)a.故有

矛盾.于是M是R的本质左理想.由R是左GP-V′-环知,单奇异左R-模R/M 是GP-内射的.又因为a2=0,所以存在b∈R,使得1+M=f(a)=ab+M,1-ab∈M.注意到Ra是弱右理想,则存在正整数n,使得(ab)n∈Ra⊆M.类似引理1可证ab∈M,1∈M,矛盾.故a=0,R是约化环.证毕.
定理1 设R是环,则下列叙述等价:
1)R是强正则环;
2)R是左(右)GP-V-环,且R的每个主左(右)理想是弱右(左)理想;
3)R为每个幂等元是中心元的左(右)GP-V′-环,且每个主左(右)理想是弱右(左)理想.
证明:1)⇒2),3)显然.下证2),3)⇒1).仅证左的情形,右的情形类似可证.
2)⇒1).由引理1和引理2知,R是约化环,则对任意的a∈R,l(a)=r(a).下证Ra+l(a)=R.若不然,则存在a∈R,使得Ra+l(a)≠R,于是存在R的极大左理想M,使得Ra+l(a)⊆MR.由R 约化知,l(an)=l(a),因此可以定义左R-模同态f:Ran→R/M;ranr+M,∀r∈R.注意到R是左GP-V-环,单左R-模R/M是GP-内射的.从而存在b∈R,使得1-anb∈M.又因为Ra是弱右理想,则存在正整数m,使得(anb)m∈Ra⊆M.类似引理1可证anb∈M,1∈M,矛盾.所以对任意的a∈R,有Ra+l(a)=R.故R是强正则环.
3)⇒1).由引理3知,R是约化环,则对任意的a∈R,l(a)=r(a).下证Ra+l(a)=R.若不然,则存在a∈R,使得Ra+l(a)≠R.类似引理3的证明知,存在R的极大本质左理想M,使得Ra+l(a)⊆MR.于是单奇异左R-模R/M是GP-内射的.类似2)⇒1)可证1∈M,矛盾.所以对任意的a∈R,有l(a)+Ra=R.故R是强正则环.证毕.
命题1 设R是中心半交换环,则下列叙述等价:
1)R是强正则环;
2)R是左GP-V′-环,且R的每个主左理想是弱右理想;
3)R是左GP-V′-环,且R的每个主右理想是弱左理想.
证明:1)⇒2),3)显然.
2)⇒1).由中心半交换环的定义,设e是幂等元,则e(1-e)=(1-e)e=0,于是对任意的a∈R,有ea(1-e)∈C(R),(1-e)ae∈C(R).从而ea(1-e)=e·ea(1-e)=ea(1-e)·e=0,则ea=eae.同理有ae=eae.故ae=ea,即幂等元e是中心元.由定理1即得结论.
3)⇒1).对任意的a∈R,若a≠0且a2=0,则存在R的极大左理想M,使得l(a)⊆MR,因此可定义左R-模同态f:Ra→R/M;rar+M,∀r∈R.易知M 是本质左理想.由R是左GP-V′-环知,单奇异左R-模R/M是GP-内射的.又因为a2=0,所以存在b∈R,使得1+M=f(a)=ab+M,1-ab=m∈M,1=ab+m.由于R 是中心半交换环,则aba∈C(R).从而有(aba)(ba)=(ba)(aba)=0,(ab)3=0,ab是幂零元.故m=1-ab有逆元,1∈M,这与M的极大性矛盾.所以a=0,R是约化环,故l(a)=r(a).
下证对任意的a∈R,aR+l(a)=R.若不然,则存在a∈R,使得aR+l(a)≠R.类似引理3的证明知,存在R的极大本质右理想K,使得aR+l(a)⊆KR.假设RaRK,则存在r,s∈R,使得ras∉K.故K+rasR=R,于是存在x∈K,t∈R,使得x+rast=1.由aR是弱左理想知,存在正整数m,使得(rast)m∈aR⊆K,则(1-x)m=(rast)m∈K,1∈K,矛盾.故RaR⊆K,RaR+l(a)⊆KR,从而存在R的极大本质左理想L,使得RaR+l(a)⊆LR.由R约化知,l(an)=l(a),因此可以定义左R-模同态g:Ran→R/L;ranr+L,∀r∈R.由R 是左 GP-V′-环知,单奇异左R-模R/L 是GP-内射的,因而存在c∈R,使得1-anc∈L.又因为anc∈RaR⊆L,则1∈L,矛盾.所以aR+r(a)=aR+l(a)=R,R是强正则环.证毕.
定理2 设R是中心半交换环,则下列叙述等价:
1)R是强正则环;
2)R是左GP-V′-环,且R的每个极大本质左理想是弱右理想;
3)R是左GP-V′-环,且R的每个极大本质右理想是弱左理想.
证明:1)⇒2),3)显然.
2)⇒1).由命题1知R约化,下证对于任意的a∈R,Ra+l(a)=R.若不然,则存在a∈R,使得Ra+l(a)≠R.类似引理3的证明知,存在R的极大本质左理想M,使得Ra+l(a)⊆MR.由R约化知,l(an)=l(a),于是可以定义左R-模同态f:Ran→R/M;ranr+M,∀r∈R.由R是左GP-V′-环知,单奇异左R-模R/M是GP-内射的,因此存在b∈R,使得1-anb∈M.又因为M 是弱右理想,则存在正整数m,使得(anb)m∈M.类似引理1可证anb∈M,1∈M,矛盾.所以对于任意的a∈R,有Ra+l(a)=R.故R是强正则环.
3)⇒1).由命题1知R约化,故l(a)=r(a).下证对任意的a∈R,aR+l(a)=R.若不然,则存在a∈R,使得aR+l(a)≠R.类似引理3的证明知,存在R的极大本质右理想K,使得aR+l(a)⊆KR.假设RaRK,则存在r,s∈R,使得ras∉K.故K+rasR=R,于是存在x∈K,t∈R,使得x+rast=1.由K 是弱右理想知,存在正整数m,使得(rast)m∈K,则(1-x)m=(rast)m∈K,1∈K,矛盾.故RaR⊆K,RaR+l(a)⊆KR,因此存在R的极大本质左理想L,使得RaR+l(a)⊆LR.由R约化知,l(an)=l(a),从而可定义左R-模同态g:Ran→R/L;ranr+L,∀r∈R.由R是左GP-V′-环知,单奇异左R-模R/L 是 GP-内射的,因而存在c∈R,使得1-anc∈L.又因为anc∈RaR⊆L,则1∈L,矛盾.所以aR+r(a)=aR+l(a)=R,R是强正则环.证毕.
引理4[7]设R是拟ZI-环,若R是GP-V′-环,则R约化.
由文献[7]中引理1.1.3知,拟ZI-环的每个幂等元是中心元.于是有:
命题2 设R是拟ZI-环,则下列叙述等价:
1)R是强正则环;
2)R是左GP-V′-环,且R的每个主左理想是弱右理想;
3)R是左GP-V′-环,且R的每个主右理想是弱左理想.
证明:1)⇒2),3)显然.由定理1可得2)⇒1).
3)⇒1).由引理4知R约化,故l(a)=r(a).下证对于任意的a∈R,aR+l(a)=R.若不然,则存在a∈R,使得aR+l(a)≠R.类似引理3的证明知,存在R的极大本质右理想K,使得aR+l(a)⊆KR.假设RaRK,则存在r,s∈R,使得ras∉K,故K+rasR=R,于是存在x∈K,t∈R,使得x+rast=1.由aR是弱左理想知,存在正整数m,使得(rast)m∈aR⊆K,从而(1-x)m=(rast)m∈K,1∈K,矛盾.故RaR⊆K,RaR+l(a)⊆KR,于是存在R的极大本质左理想L,使得RaR+l(a)⊆LR.由R约化知,l(an)=l(a),因此可定义左R-模同态g:Ran→R/L;ranr+L,∀r∈R.由R是左GP-V′-环知,单奇异左R-模R/L是GP-内射的,因而存在c∈R,使得1-anc∈L.又因为anc∈RaR⊆L,则1∈L,矛盾.所以aR+r(a)=aR+l(a)=R,R是强正则环.证毕.
2 广义(弱)正则环的强正则性
引理5[4]若环R是广义正则环,则R是左非奇异环,且J(R)=0.
定理3 设R是环,则下列叙述等价:
1)R是强正则环;
2)R是广义正则环,且R的每个主左理想是弱右理想;
3)R是广义正则环,且R的每个主右理想是弱左理想.
证明:1)⇒2),3)显然.仅证2)⇒1),类似可证3)⇒1).
2)⇒1).由引理1和引理5知R约化,则R的每个幂等元是中心的.又因为R是广义正则环,则对任意的a∈R,Ra=∑Rei,其中ei是中心幂等元.令a=r1e1+…+rnen,则有
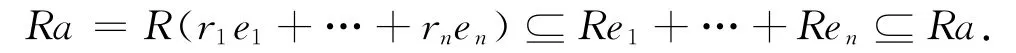
从而有Ra=Re1+…+Ren.令f1=e1+e2-e1e2,则f21=f1,e1f1=e1,e2f1=e2,于是
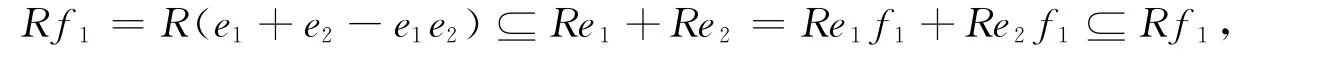
故Re1+Re2=Rf1.再令f2=f1+e3-f1e3,…,fn-2=fn-3+en-1-fn-3en-1,e=fn-2+en-fn-2en.如此继续下去,有
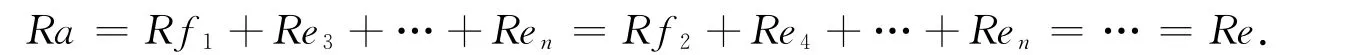
则存在b,r∈R,使得a=re,e=ba,故a=ae=ea=ba2,即R是强正则环.证毕.
命题3 设R是J-环,则下列叙述等价:
1)R是强正则环;
2)R是左弱正则环,且R的每个极大本质左理想是弱右理想;
3)R是左弱正则环,且R的每个极大本质右理想是弱左理想;
4)R是右弱正则环,且R的每个极大本质左理想是弱右理想;
5)R是右弱正则环,且R的每个极大本质右理想是弱左理想.
证明:1)⇒2),3),4),5)显然.下证2),3)⇒1),类似可证4),5)⇒1).
2)⇒1).因为R是左弱正则环,故J(R)=0.又R是J-环,则N(R)=J(R)=0,从而R是约化环.下证l(a)+Ra=R.若l(a)+Ra≠R,则存在R的极大左理想M,使得l(a)+Ra⊆MR.易知M 是R的本质左理想.若不然,则存在e2=e∈R,使得M=Re=l(1-e).由a∈Ra⊆M=l(1-e)及R约化知,a(1-e)=0=(1-e)a.故有1-e∈l(a)⊆l(1-e),1-e=(1-e)2=0,1=e∈M,矛盾.于是M是R的本质左理想,从而M是弱右理想.又由于R是左弱正则环,故有Ra=RaRa,则存在ri,si∈R,使得a=∑riasia,因此(1-∑riasi)a=0,1-∑riasi∈l(a)⊆M.若∑riasi∉M,则存在正整数k,使得rkask∉M.于是M+Rrkask=R,则存在x∈M,r∈R,使得x+rrkask=1.注意到M是弱右理想且a∈M,则存在正整数n,使得(rrkask)n∈M,则(1-x)n=(rrkask)n∈M,1∈M,矛盾.所以对于任意的a∈R,有l(a)+Ra=R.故R是强正则环.
3)⇒1).由上述证明知R是约化环,则对于任意的a∈R,l(a)=r(a).下证r(a)+aR=R.若不然,则存在R的极大右理想K,使得l(a)+aR=r(a)+aR⊆KR.类似2)⇒1)的证明知,K是R的本质右理想,则K是弱左理想.又因为R是左弱正则环,故有Ra=RaRa.因此存在ri,si∈R,使得a= ∑riasia,从而(1-∑riasi)a=0,1-∑riasi∈l(a)⊆K.若∑riasi∉K,则存在正整数k,使得rkask∉K.于是K+rkaskR=R,则存在x∈K,r∈R,使得x+rkaskr=1.注意到K是弱左理想且a∈K,则存在正整数n,使得(rkaskr)n∈K,则(1-x)n=(rkaskr)n∈K,1∈K,矛盾.所以对于任意的a∈R,有l(a)+aR=r(a)+aR=R.故R是强正则环.证毕.
定理4 设R是环,则下列叙述等价:
1)R是强正则环;
2)R是左弱正则环,且R的每个主左理想是弱右理想;
3)R是左弱正则环,且R的每个主右理想是弱左理想;
4)R是右弱正则环,且R的每个主左理想是弱右理想;
5)R是右弱正则环,且R的每个主右理想是弱左理想.
证明:1)⇒2),3),4),5)显然.下证2),3)⇒1),类似可证4),5)⇒1).
2)⇒1).因为R是左弱正则环,故J(R)=0.由引理1知R是约化环.下证l(a)+Ra=R.若l(a)+Ra≠R,则存在R的极大左理想M,使得l(a)+Ra⊆MR.由于R是左弱正则环,故有Ra=RaRa,则存在ri,si∈R,使得a= ∑riasia,从而(1-∑riasi)a=0,1-∑riasi∈l(a)⊆M.若∑riasi∉M,则存在正整数k,使得rkask∉M.于是M+Rrkask=R,则存在x∈M,r∈R,使得x+rrkask=1.注意到Ra是弱右理想,则存在正整数n,使得(rkask)n∈Ra⊆M,从而(1-x)n=(rkask)n∈M,1∈M,矛盾.所以对于任意的a∈R,有l(a)+Ra=R.故R是强正则环.
3)⇒1).由上述证明知R是约化环,则对于任意的a∈R,l(a)=r(a).下证r(a)+aR=R.若不然,则存在R的极大右理想K,使得l(a)+aR=r(a)+aR⊆KR.又因为R是左弱正则环,故有Ra=RaRa,则存在ri,si∈R,使得a=∑riasia,从而(1-∑riasi)a=0,1-∑riasi∈l(a)⊆K.若∑riasi∉K,则存在正整数k,使得rkask∉K.于是K+rkaskR=R,则存在x∈K,r∈R,使得x+rkaskr=1.注意到aR是弱左理想且a∈K,则存在正整数n,使得(rkaskr)n∈aR⊆K,从而(1-x)n=(rkaskr)n∈M,1∈K,矛盾.所以对于任意的a∈R,有l(a)+aR=r(a)+aR=R.故R是强正则环.证毕.
[1]XIAO Guang-shi,TONG Wen-ting.Rings Whose Every Simple Left R-Modules Is GP-Injective[J].Southeast Asian Bulletin of Math,2006,30(5):969-980.
[2]Goodearl K R.Von Neumann Regular Rings[M].Tallahassee:Krieger Publishing Company,1991.
[3]Szsz F A.Radicals of Rings[J].Akacemidi Kiado Budapest,1981,23(1):201-231.
[4]ZHANG Ju-le.Characterizations of Strong Regular Rings[J].Northeast Math J,1994,10(3):359-364.
[5]WU Guo-ying,WU Jun.On the Strong Regularity of J-Rings[J].Journal of Shandong University:Natural Science,2012,47(2):71-73.(吴国英,吴俊.关于J-环的强正则性 [J].山东大学学报:理学版,2012,47(2):71-73.)
[6]CHEN Wen-bing,YIN Xiao-bin.Some Properties and Characterizations on Wnil-Injective Modules[J].Journal of Jilin University:Science Edition,2011,49(6):985-988.(陈文兵,殷晓斌.Wnil-内射模的若干性质及刻画 [J].吉林大学学报:理学版,2011,49(6):985-988.)
[7]WANG Rui.The Regularity of Some Special Rings[D].Wuhu:Anhui Normal University,2011.(王瑞.几类特殊环的正则性 [D].芜湖:安徽师范大学,2011.)(责任编辑:赵立芹)
