弱M-拟Armendariz环的性质及等价刻画
2014-10-25丁婷婷张培雨
丁婷婷,吴 俊,张培雨
(安徽师范大学 数学计算机科学学院,安徽 芜湖241003)
本文所有的环均指有单位元的结合环.用N(R)表示环R的所有幂零元集合,Tn(R)表示环R上的n阶上三角矩阵环,M是幺半群,e是M 的单位元.Rege等[1]通过引入Armendariz环的概念,研究了Armendariz环与半交换环之间的关系.如果
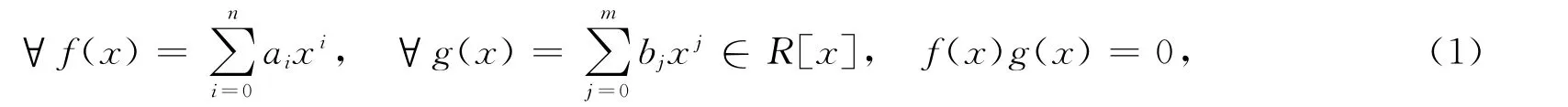
有aibj=0(∀0≤i≤n;0≤j≤m),则环R 称为 Armendariz环[1].目前,对 Armendariz环及Armendariz环的推广研究已取得了丰富成果[2-10].如果
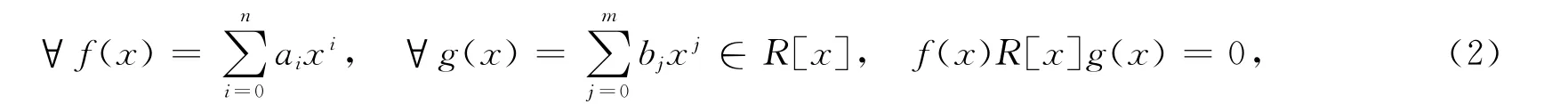
有aiRbj=0(∀0≤i≤n;0≤j≤m),则环 R 称为拟 Armendariz环[2].Ebrahim[3]引入了M-拟Armendariz环的概念,并研究了其相关性质.如果
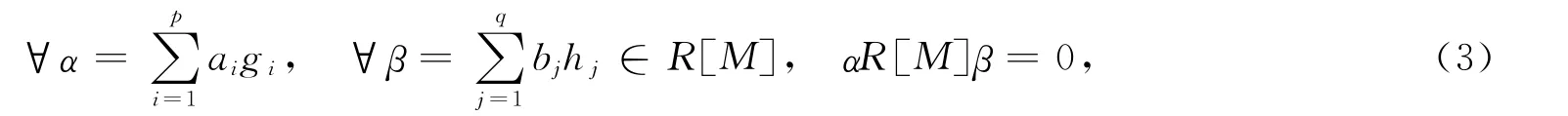
有aiRbj=0(∀1≤i≤p;1≤j≤q),则环R 称为M-拟 Armendariz环[3].如果式(2)成立,且有aiRbj⊆N(R)(∀0≤i≤n;0≤j≤m),则环 R 称为拟弱 Armendariz环[4].如果式(3)成立,且有aiRbj⊆N(R)(∀1≤i≤p;1≤j≤q),则环R称为弱M-拟Armendariz环[5].
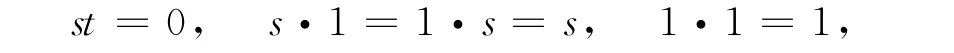
若对M的任意两个非空有限子集A,B,存在g∈M唯一表示成ab的形式,则幺半群M称为u.p.-幺半群,其中:a∈A;b∈B.若对任意的a∈I,存在x∈I,使得ax=a,则R的理想I称为右s-unital的.若对任意的a∈R,lR(Ra)◁R是右s-unital的,则环R称为左APP-环.
文献[6]证明了M是幺半群,N是u.p.-幺半群,R是左APP-环,则R是M×N-拟Armendariz环当且仅当R是M-拟Armendariz环.对于弱M-拟Armendariz环有如下结论.
定理1 设M,N是u.p.-幺半群,R是左APP-环,则下列命题等价:
1)R是弱M×N-拟Armendariz环;
2)R是弱M-拟Armendariz环;
3)R是弱N-拟Armendariz环.

则
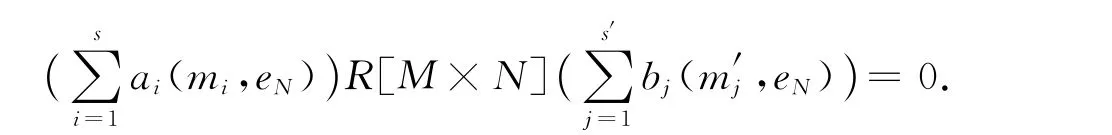
由于R 是弱M×N-拟 Armendariz环,所以对任意的i,j,有aiRbj⊆N(R).故R 是弱M-拟Armendariz环.
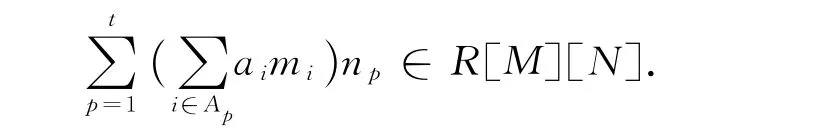
易证存在环同构
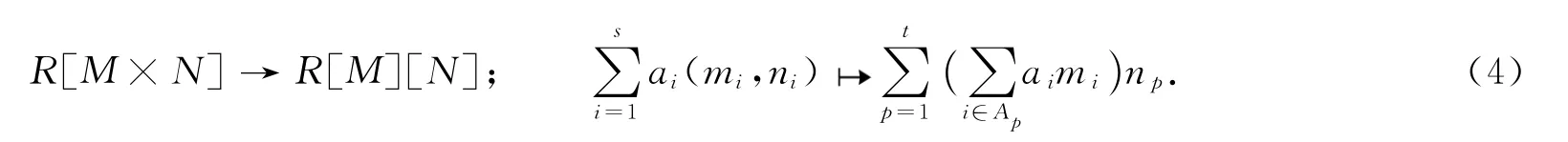
设
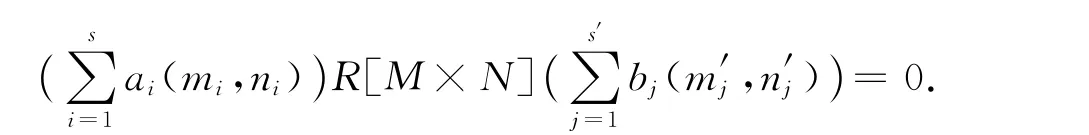
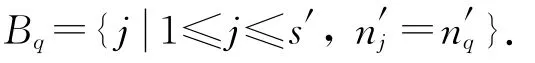
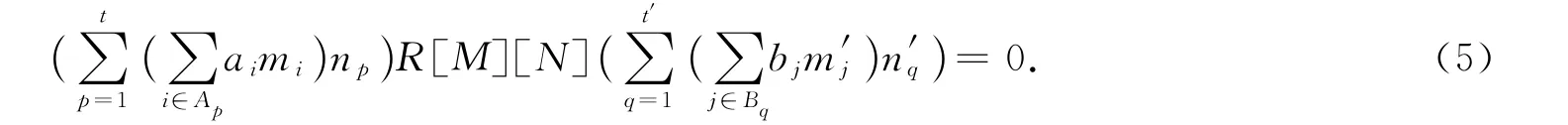
由文献[6]中推论2.5知R[M]是N-拟Armendariz环,因此对任意的p,q,有
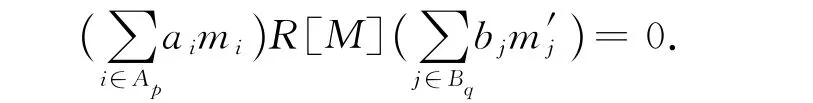
由于R是弱M-拟Armendariz环,所以aiRbj⊆N(R),i∈Ap,j∈Bq.因此aiRbj⊆N(R),1≤i≤s,1≤j≤s′.故R是弱M×N-拟Armendariz环.
1)⇔3).注意到R[M×N]≅R[N×M],由类似于1)⇔2)的证明方法即证.
推论1 设M是u.p.-幺半群,R是左APP-环,则下列命题等价:
1)R是弱M-拟Armendariz环;
2)R是弱ℤ-拟Armendariz环;
3)R是弱ℕ-拟Armendariz环;
4)R是弱(M×ℤ)-拟Armendariz环;
5)R是弱(M×ℕ)-拟Armendariz环.
证明:由于ℤ,ℕ是u.p.-幺半群,故由定理1即证.
命题1 设M是交换幺半群,R是弱M-拟Armendariz环,则M是可消的.
证明:设m,g,h∈M,mg=mh,但g≠h,则对任意的r∈R,m′∈M,

故
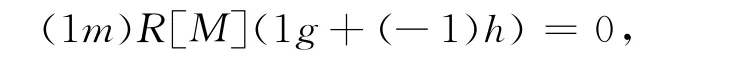
但1·1·1=1∉N(R),与R是弱M-拟Armendariz环矛盾.所以M是可消的.
如果式(1)成立,且有aibj∈N(R)(∀0≤i≤n;0≤j≤m),则环R称为弱Armendariz环[7].
对于幺半群M,用G(M)表示M的最大子群.文献[6]证明了若M 是交换幺半群,G(M)={e},R是拟Armendariz和M-拟Armendariz环,则R[M]是拟Armendariz环.对于幺半群M,若R是拟弱Armendariz和弱M-拟Armendariz环,R[M]是否是拟弱Armendariz环未知.而对于半交换环R,则有如下结论.
命题2 设M是交换幺半群,G(M)={e},R是半交换和弱M-拟Armendariz环,则R[M]是拟弱Armendariz环.
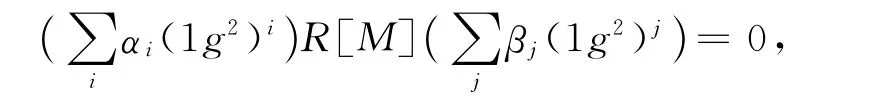
即
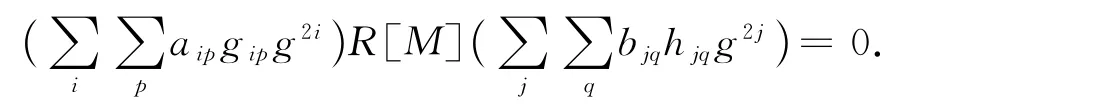
若对某个i′,i″,有gi′p′g2i′=gi″p″g2i″.当i′=i″时,由命题1知 M 是 可消的,则 gi′p′=gi′p″,故p′=p″.因此不失一般性,设i′>i″,因为 M 是可消的,故gi′p′g2(i′-i″)=gi″p″.易见对任意的i,j,p,q,gip,hjq均有逆元,故gip,hjq∈G(M)={e}.则可令αi=aie,βj=bje,即有
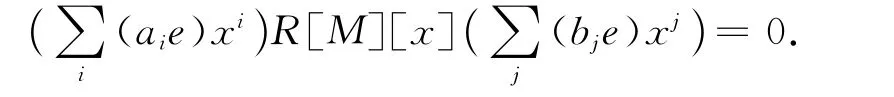
αiγβj= (air1bj)m1+ (air2bj)m2+ … + (airnbj)mn, air1bj,air2bj,…,airnbj∈ N(R).由文献[8]中引理3知αiγβj∈N(R[M]),所以R[M]是拟弱Armendariz环.
若对某个j′,j″,有hj′q′g2j′=hj″q″g2j″,则类似于上述证明可得R[M]是拟弱 Armendariz环.
若每组gipg2i不同,每组hjqg2j也不同.由于R是弱M-拟Armendariz环,所以aipRbjq⊆N(R).任取γ=r1m1+r2m2+…+rnmn∈R[M],则有
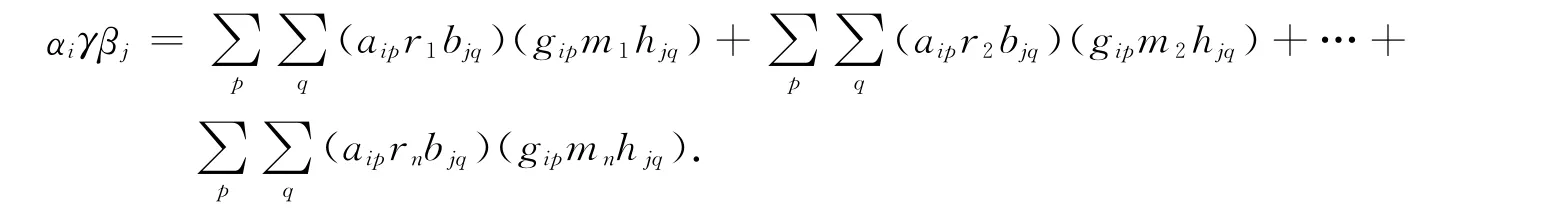
由文献[7]中引理3.1和文献[8]中引理3知αiγβj∈N(R[M]),所以R[M]是拟弱Armendariz环.
由文献[6]知,M是幺半群,R是左APP-环,则R是M-拟Armendariz环当且仅当Sn(R)是M-拟Armendariz环.但对于弱M-拟Armendariz环有下列结论.
定理2 设M是幺半群,R是环,则下列命题等价:
1)R是弱M-拟Armendariz环;
2)Tn(R)是弱M-拟Armendariz环.
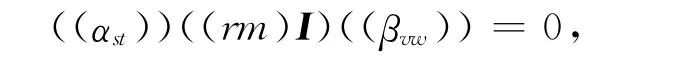

下证AiTn(R)Bj⊆N(Tn(R)).任取C=(cef)∈Tn(R),则



设R为环,M为(R,R)-双模,R对于M 的平凡扩张T(R,M)=R⊕M,其中运算为

易知
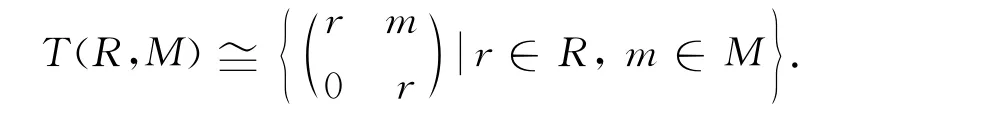
推论2 设M是幺半群,R是环,则下列命题等价:
1)R是弱M-拟Armendariz环;
2)Sn(R)是弱M-拟Armendariz环;
3)T(R,R)是弱M-拟Armendariz环;
4)R[x]/(xn)是弱 M-拟 Armendariz环.
证明:注意到
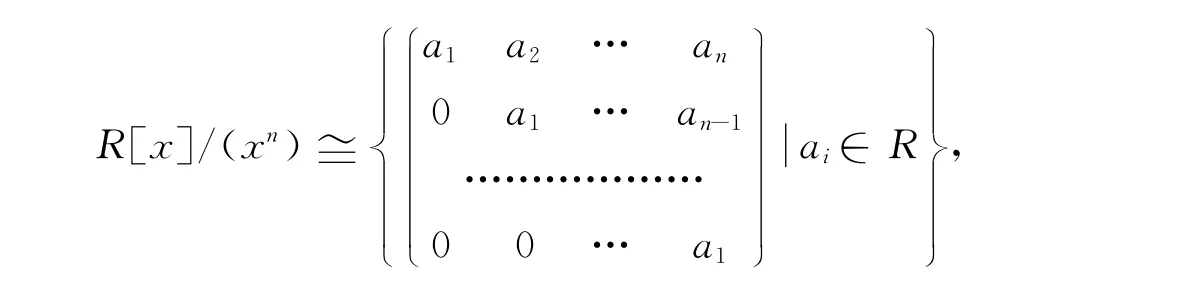
由定理2的证明方法即证上述命题等价.
注1 由定义可知,M-拟Armendariz环一定是弱M-拟Armendariz环,下面的例子说明反之不成立.
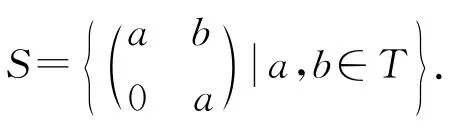
如果对任意的n∈N,m∈M,有nm∈N(mn∈N),则非空子集N是幺半群M 的右(左)理想.若N既是M的右理想,又是M的左理想,则称N是M的理想.
命题3 设N是幺半群M 的右(左)理想,且在N中存在M 的一个左(右)可消元.若R是弱N-拟Armendariz环,则R是弱M-拟Armendariz环.
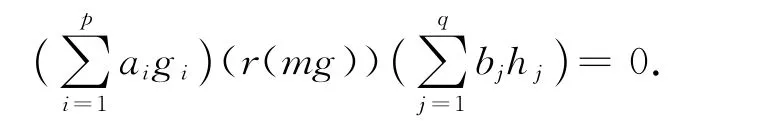
两边同时左乘Ig得
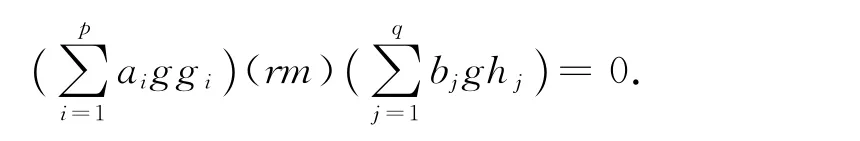
因此

由于R是弱N-拟Armendariz环,所以对任意的i,j,有aiRbj⊆N(R).因此R是弱M-拟Armendariz环.
推论3[5]设M 是可消的幺半群,N 是M 的理想.若R是弱N-拟Armendariz环,则R是弱M-拟Armendariz环.
命题4 设M是幺半群,R是弱M-拟Armendariz环.若I◁R,则I是弱M-拟Armendariz环.

则αR[M][(se)β]=0.由于 R 是弱 M-拟 Armendariz环,所以aiR(sbj)⊆N(R).特别地,aisbj∈N(R)∩I=N(I),即aiIbj⊆N(I).所以I是弱M-拟Armendariz环.
命题5 设M是幺半群,R1,R2是环,则下列命题等价:
1)R1,R2是弱M-拟Armendariz环;
2)R1×R2是弱M-拟Armendariz环.
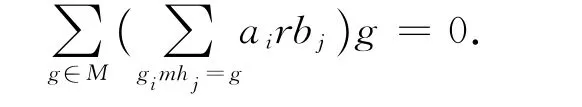
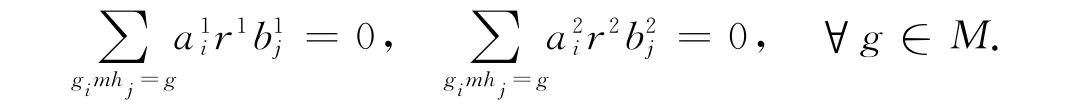
于是
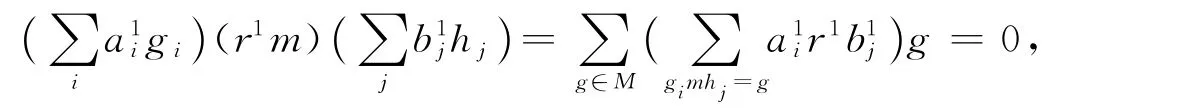
故
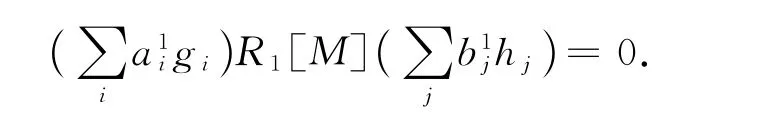
类似可得
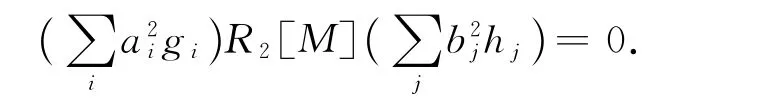
由于R1,R2是弱M-拟Armendariz环,所以对任意的i,j,有

则
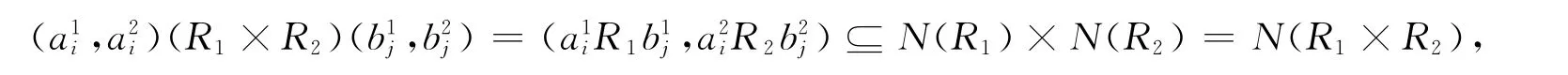
即
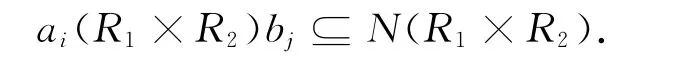
所以R1×R2是弱M-拟Armendariz环.
2)⇒1).R1≅R1×{0},R2≅{0}×R2且R1×{0},{0}×R2是R1×R2的理想,由命题4即证.
推论4 设 M 是幺半群,Ri(i∈I={1,2,…,n})是环,则下列命题等价:
1)对于每个i∈I,Ri是弱M-拟Armendariz环;
证明:类似于命题5可证1)⇔2).
[1]Rege M B,Chhawchharia S.Armendariz Rings[J].Pro Japan Acad Ser A Math Sci,1997,73:14-17.
[2]Hirano Y.On Annihilator Ideals of a Polynomial Ring over a Noncommutative Ring[J].J Pure Appl Algebra,2002,168(1):45-52.
[3]Ebrahim H.Quasi-Armendariz Rings Relative to a Monoid[J].J Pure Appl Algebra,2007,211(2):374-382.
[4]WU Bin.Quasi-weak Armendariz Rings[J].Journal of Gansu Sciences,2008,20(2):24-26.(武斌.拟-弱Armendariz环 [J].甘肃科学学报,2008,20(2):24-26.)
[5]XIE Xiao-juan,SONG Xian-mei.Weak M-Quasi-Armendariz Rings[J].Journal of Anhui Normal University:Natural Science,2012,35(2):123-126.(解晓娟,宋贤梅.弱 M-拟 Armendariz环 [J].安徽师范大学学报:自然科学版,2012,35(2):123-126.)
[6]LIU Zhong-kui,ZHANG Wen-hui.Quasi-Armendariz Rings Relative to a Monoid [J].Comm Algebra,2008,36(3):928-947.
[7]LIU Zhong-kui,ZHAO Ren-yu.On Weak Armendariz Rings[J].Comm Algebra,2006,34(7):2607-2616.
[8]ZHANG Cui-ping,CHEN Jian-long.Weak M-Armendariz Rings[J].Journal of Southest University:English Edition,2009,25(1):142-146.
[9]LIU Zhong-kui.Armendariz Rings Relative to a Monoid[J].Comm Algebra,2005,33(3):649-661.
[10]Baser M,Kaynarca F.Weak Quasi-Armendariz Rings[J].Algebra Collq,2011,18(4):541-552.
