基于pair-copula的全国社保基金委托投资组合La_VaR测度研究
2014-10-25江红莉姚洪兴
江红莉,姚洪兴
基于pair-copula的全国社保基金委托投资组合La_VaR测度研究
江红莉,姚洪兴
(江苏大学财经学院,江苏镇江 212013)
社保基金是社会保障事业健康发展的物质基础,安全性和流动性是其投资的首要原则。全国社保基金作为一类特殊的、可以进入资本市场投资的社保基金,其风险管理显得尤为重要。针对全国社保基金投资组合风险测度研究不足的现状,提出了全国社保基金投资组合经流动性调整的市场风险(La-VaR)测度的pair-copula-GARCH-EVT模型。与传统的copula模型相比,pair-copula方法不仅考虑了维数的影响,而且还能灵活地选择copula的类型。实证研究表明,pair-copula对社保基金经流动性调整的市场风险建模的效果优于传统的多维copula模型。
全国社保基金,投资组合,经流动性调整的市场风险,pair-copula,La-VaR
一、引言
社保基金是社会保障制度的物质基础,其安全和保值增值关系到社会保障事业的健康发展。为实现社保基金的保值增值,我国进行了诸多有价值的探索与实践。2000年成立了全国社会保障基金理事会(简称社保基金会),负责管理全国社会保障基金(简称全国社保基金)。全国社保基金为中央政府集中的国家战略储备基金,由中央财政拨入资金、国有股减持或转持所获资金和股权资产、经国务院批准以其他方式筹集的资金及其投资收益构成。社保基金会管理的资金由社保基金会直接运作与社保基金会委托投资管理人运作相结合,后者可以在资本市场上运作,可以投资股票、债券、基金等。根据《2012年全国社会保障基金年度报告》,自成立以来至2012年报告期末,社保基金会管理的基金累计投资收益额为3492.45亿元,年均投资收益率为8.29%,高于同期通货膨胀率①。在老龄化越来越严重、通货膨胀率高企以及资本市场尚不完善的情境下,为了实现社保基金的保值增值,能否让更多的社保基金进入资本市场?要回答这一问题,必须首先测度全国社保基金在资本市场上投资所承担的风险。
二、文献综述
市场风险是指由资产价格波动导致的投资者收益的不确定性。流动性风险源于流动性的不足,是指资产不能按照市场价格立即变现而使变现价格产生的不确定性。投资者尤其是机构投资者变现资产的过程不可避免地将影响资产价格,产生流动性风险。上世纪90年代以来,随着VaR技术在风险管理方面的广泛应用,一些学者对传统的VaR方法进行扩展,提出了经流动性调整的VaR模型(Liquidity-adjusted VaR,简称La-VaR)。Qi、Gregor等学者研究了经流动性调整的日间VaR[1-2]。谢福座、江红莉等学者分别基于静态和时变copula模型研究了经流动性调整的市场风险La-VaR[3-4]。
现有关于经流动性调整的市场风险研究,主要是基于单资产的。对于投资组合而言,经流动性调整的市场风险存在两个流动性风险因子和两个市场风险因子。传统的维copula函数对多资产建模往往只有一个参数,没有考虑到维数的影响,而事实上投资组合中不同风险因子间的相关性往往不同,这就可能导致在分析多种风险因子间的相依结构时出现误差,pair-copula模型可以有效地避免此问题。Bedford等学者引入了一种构造复杂多元相关结构模型的新方法,它将多元联合密度函数分解成一系列pair-copula模块和边缘密度函数的乘积,为copula方法推广到高维情况提供了理论基础[5]。相比于经典分级模型,当变量间不存在条件独立性时,pair-copula模块构建不要求条件独立假设,因此,这种新的方法在描述高维相关构建时就更加灵活[6],常被用于研究高维相依性和投资组合风险测度。Kim、Marcelo、陈清平等学者基于pair-copula模型研究了高维相依结构[7-9]。张高勋等学者基于pair-copula模型研究资产组合VaR,发现相比基于传统copula方法的VaR模型,pair-copula模型在描述高维相关结构时更加灵活,由此构建的VaR模型更接近实际发生的损失[10]。
关于我国社保基金投资组合风险测度,江红莉等先后采取copula、时变copula以及pair-copula方法进行了研究,但仅仅研究了市场风险,没有考虑流动性风险[11-12]。对于以股票、基金、债券等为主要投资工具的全国社保基金而言,市场风险和流动性风险是重要的风险因子。在指令驱动市场中,如A股市场,如果投资者投资理念趋同、持股集中或者发生羊群效应,有可能进一步加大流动性风险[13]。因此,在测度社保基金委托投资的市场风险时,有必要考虑流动性风险因子。本文基于pair-copula模型测度社保基金委托投资组合经流动性调整的市场风险:首先,基于GARCH-EVT对每个风险因子建模,得到独立同分布的序列,然后,确定pair-copula的分解类型,采用极大似然函数估计法估计pair-copula模型的参数;最后,结合pair-copula参数估计的结果,模拟生成pair-copula分解模型的仿真序列,进行Kuppiec检验,计算投资组合经流动性调整的市场风险La_VaR值。
三、市场风险因子与流动性风险因子
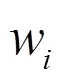
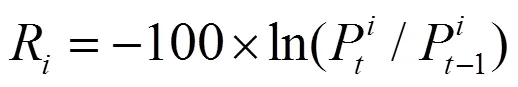
若考虑流动性风险,则资产的资产损失率为[3]:
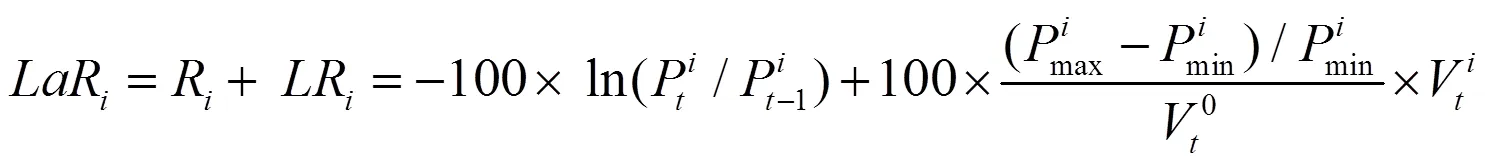
则考虑了流动性风险的投资组合损失率为:
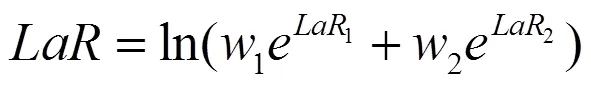
由资产1和资产2构建的投资组合,其经流动性调整的市场风险包含四个风险因子:两个市场风险因子1和2,两个流动性风险因子1和2。要准确地测度投资组合经流动性调整的市场风险,必须准确地刻画这四个风险因子间的相关结构。
四、pair-copula建模及参数估计
(一)pair-copula的理论基础
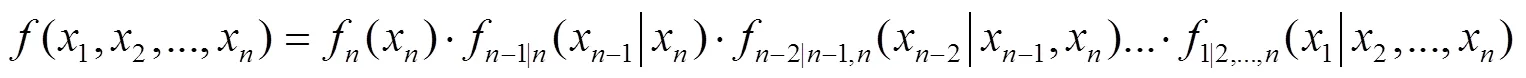
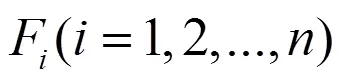
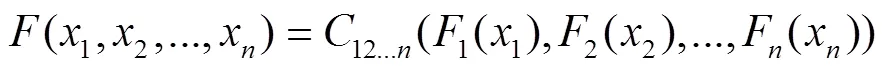
对(5)式两边求导,则有
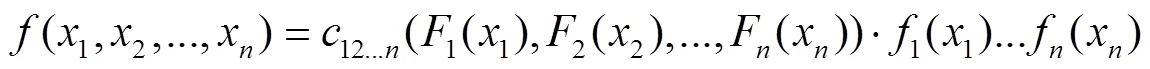
由此可知,(4)式中的每一项可以分解为适当的pair-Copula函数乘以一个条件边缘密度,即
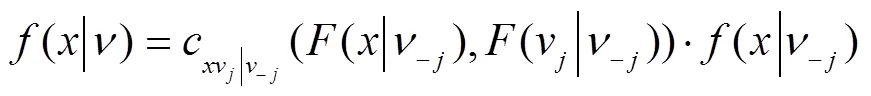
由(4)-(7)式可知,在合适的分解规则下,多变量的联合密度函数可以表示为一系列的pair-copula密度函数与边缘条件概率密度函数的乘积。
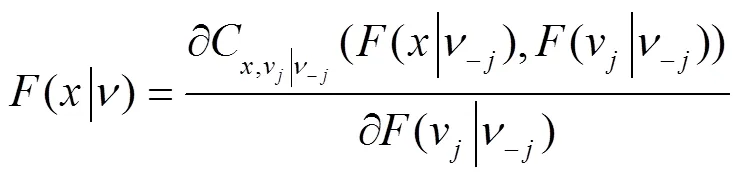
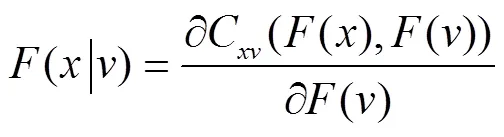
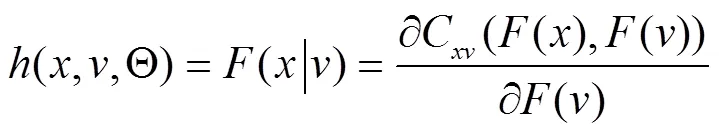
(二)高维联合分布下的pair-copula建模
对于高维联合分布,存在多种pair-copula结构。Bedford等学者引入了称之为“正则藤(the regular vine)”的图形建模工具来描述这些pair-copula[5]。N维变量的藤是一类树的集合,树的边是树+1的节点,=1,2,……,N-2,每棵树的边数均取最大。C(Canonical)藤和D藤是两类最特殊的藤,其中,C藤在每棵树T中仅有唯一的点连接到-条边;D藤树中任一结点所连接的边的条数最多为2。C藤和D藤的适用范围不同:当数据集中出现引导其他变量的关键变量时,适合用C藤建模,而当变量相对独立时,则适合用D藤建模。
极大似然估计法是参数估计的常用方法,与传统的维copula参数估计方法不同,对pair-copula模型进行极大似然估计前,必须先估计出每棵树的参数初值。pair-copula参数估计的基本思路:第一步,基于原始数据估计第1棵树上的copula函数的参数;第二步,基于第一步参数估计的结果及h函数,计算观测值(即条件分布函数值),基于此观测值值估计第2棵树上的copula函数的参数;第三步,重复第一步和第二步,直到计算出每棵树上copula函数的参数。将第一、二、三步所得的参数值作为初始值,最大化总体似然函数,求得最终的参数估计值。
以4维C藤为例,具体说明pair-copula-t参数的估计步骤。
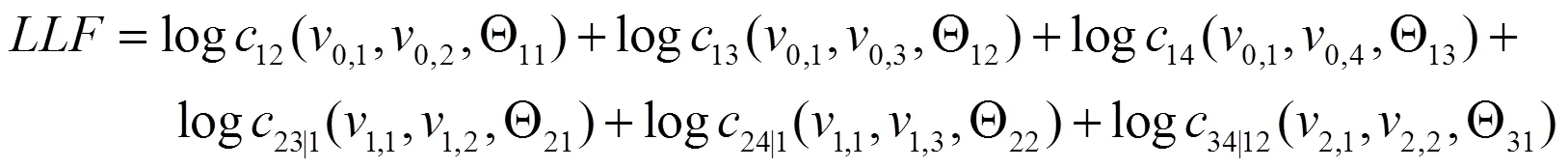
得到参数估计的最终值。通常,初始值与最终值的差别不大。
(三)pair-copula模型的仿真序列生成
五、实证研究
(一)样本选择及描述性统计
尽管社保基金可以投资于股票、债券、基金、企业债和金融债等金融产品,但出于安全性和收益性考虑,股票和债券是社保基金投资的主要金融产品。基于简单但不失一般性的原则,选择沪深300指数代表股票投资,国债指数代表国债投资;假设投资于股票的社保基金权重为1=0.4223,投资于国债的社保基金权重为2=0.5777,模拟构造社保基金的投资组合。样本考察期为2008年5月10到2013年12月10日,共1363组数据。所有数据来源于大智慧软件,数据处理采用S-plus8.0和Matlab7.9。
样本考察期内,根据沪深300指数和国债指数的成交额,假定社保基金所投资的股票日成交额为109元,即V1=109;假定社保基金所投资的国债日成交额为108元,即V2=108。为方便叙述,沪深300指数和国债指数的市场风险因子分别记为HR和GR,流动性风险因子分别记为HL和GL,其描述性统计如表1所示。
由表1可知,在样本观察期间内,沪深300指数和国债指数的平均收益均为正(表1中给出的是负对数对数收益率)。峰度统计量和J-B检验统计量均表明无论是沪深300指数还是国债指数的,其市场风险因子和流动性风险因子均不服从正态分布。ARCH效应检验表明,滞后10阶,沪深300指数和国债指数的市场风险因子和流动性风险因子都具有明显的条件异方差性。Ljung-Box Q统计量显示,滞后10阶,在5%的显著水平下,市场沪深300指数和国债指数的市场风险因子和流动性风险因子均具有自相关性。单位根ADF检验表明,所有的序列都是平稳的。
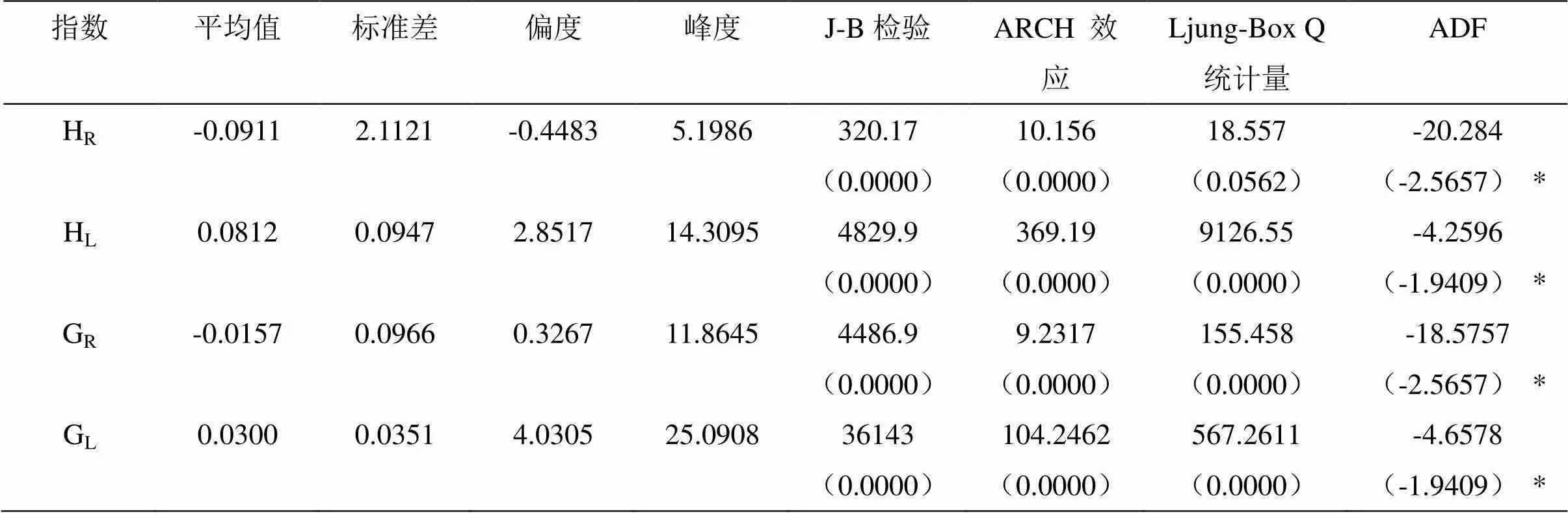
表1 :市场风险因子和流动性风险因子的描述性统计
注:*表示5%的显著水平所对应的临界值,其余的()内的数值表示相伴概率p,Ljung-Box Q统计量和ARCH效应检验给出的是滞后10阶的检验结果。
(二)边缘分布参数估计
基于Ljung-Box Q检验,并结合AIC和SC准则,最终选择AR(2)-GARCH(1,1)-t对HR建模,选择AR(5)-GJR-GARCH-t对HL建模,AR(2)-GARCH-t对GR建模,选择AR(6)-GJR-GARCH-t对GL建模。为节约篇幅,略去均值方程的参数估计结果,仅给出波动方程的参数估计结果,见表2。
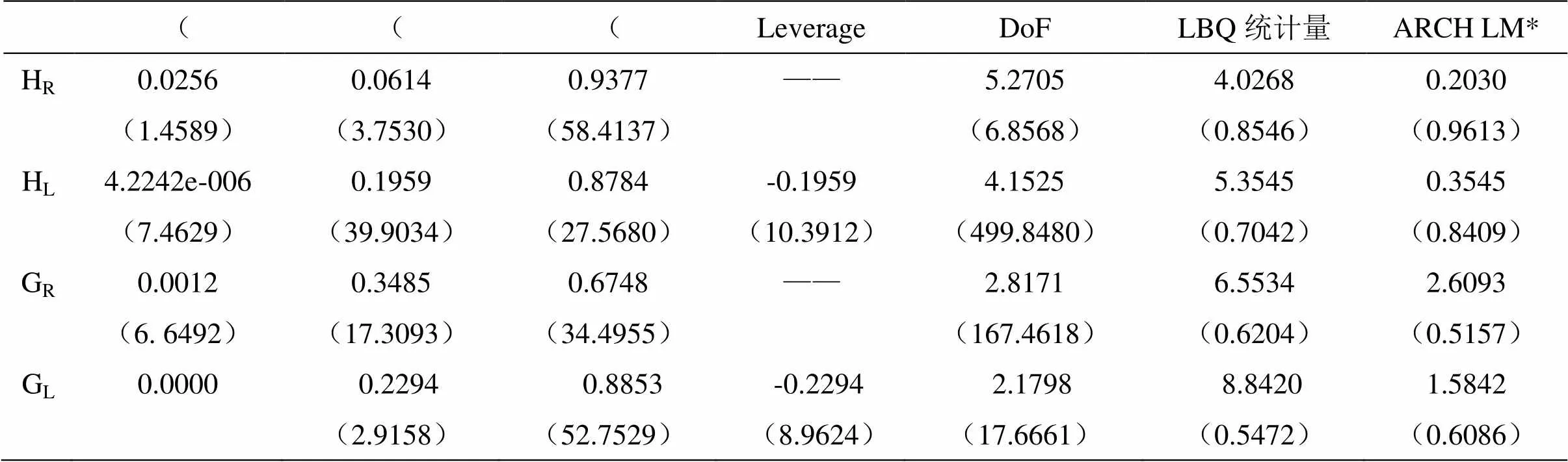
表2 :HR、HL、GR和GL序列边际分布建模参数估计结果
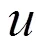

表3 :HR、HL、GR和GL的尾部分布参数估计结果
(三)pair-copula模型的参数估计
基于Kendall’S tau及C藤、D藤的适用范围,选择合适的pair-copula分解类型。经GARCH-EVT过滤后的两两标准残差序列间的Kendall’S tau值如表4所示。

表4 :HR、HL、GR和GL间的Kendall’S tau值
图1:风险建模的C藤结构分解图
根据Kendall’s,相关性从强到弱依次为:HL-GL、HL-GR、HR-GR、GL-GR、HL-HR、HR-GL,虽然总体而言,序列间的相关性都较弱,但是HL与其他序列之间具有引导关系,可以认为HL是先导变量,比较适合用C藤分解,故选择C藤pair-Copula建模,结构分解如图1。
选择copula-t作为pair-copula建模的类型,基于极大似然估计法估计模型参数,结果如表5。

表5 :pair-copula-t的参数估计结果
同时采用4维copula-t模型对社保基金投资组合经流动性调整的市场风险建模。copula-t模型的自由度的估计值为4.8990,对数似然函数值为914.78。再结合表5可知,4维copula-t模型对社保基金投资组合经流动性调整的市场风险建模效果劣于pair-copula-t的建模效果。
(四)投资组合风险的仿真计算及后试检验
估计出pair-copula模型的参数后,采用Monte Carlo方法模拟服从pair-copula分解的联合分布函数的仿真序列,根据投资组合中资产的权重,计算投资组合的收益率,进而计算投资组合的La_VaR。根据表5给出的pair-copula参数估计最终值,仿真5000次,得出了样本期内pair-copula-t模型预测失败的天数、失败率以及LR值,结果如表6所示。
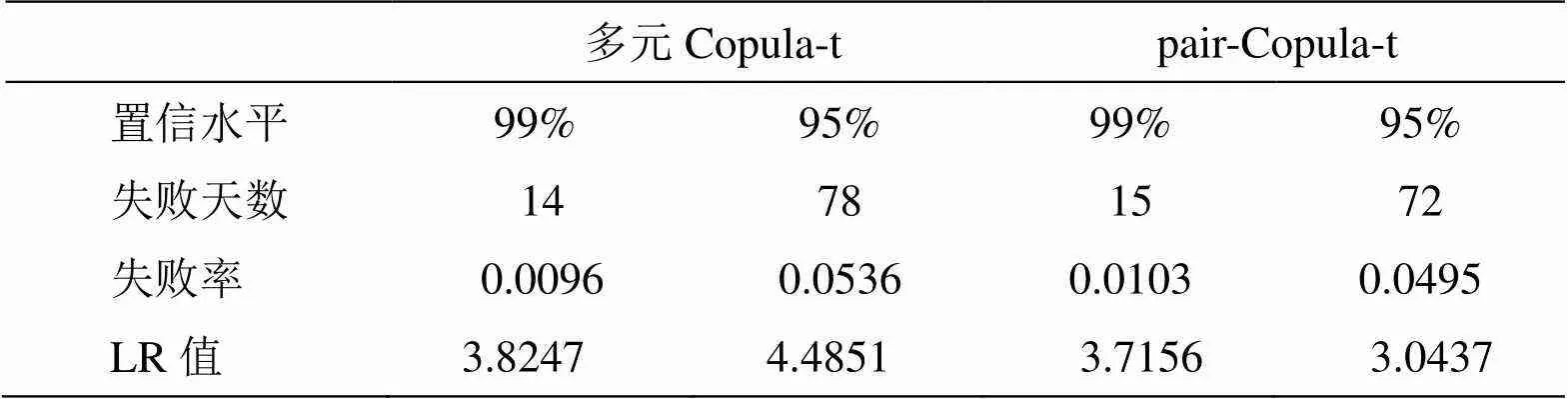
表6 :投资组合La_VaR预测的失败次数及失败率及LR值
由表6可以看出,在95%的置信度下,拒绝了copula-t模型,而无论95%的置信度还是99%的置信度,均接受了pair-copula模型,进一步说明pair-copula-t模型的建模效果优于多元copula-t模型的建模效果。
由此,基于pair-copula模型对模拟的社保基金投资组合建模,得出:95%置信度下,当金融市场上股票的成交额为109元和国债的成交额为108元时,社保基金经流动性调整的市场风险La_VaR为0.4797单位。
六、结语
社保基金进入资本市场,最终目的是在保证安全性、流动性的前提下实现收益最大化,因此,在测度社保基金投资组合的市场风险时,有必要考虑其流动性风险。与传统的多元copula函数相比,pair-copula分解不仅考虑了维数的影响,能够更好地刻画投资组合中不同资产风险两两之间的相关性,而且可以根据实际数据拟合的情况对每一对copula函数选择不同类型的copula函数,建模更加灵活。本文将pair-copula方法应用到投资组合经流动性调整的市场风险测度中,为测度投资组合经流动性调整的市场风险提供了一种新的方法,并基于该方法测度了社保基金投资组合经流动性调整的市场风险。Kupiec检验说明,pair-copula对社保基金经流动性调整的市场风险建模的效果优于传统的多维copula模型。
[注释]
① 社保基金会成立至2005年,社保基金会管理的是全国社保基金;2006-2008年,管理的基金有全国社保基金、个人账户基金和行业统筹基金;2009-2011年,社保基金会管理的基金有全国社保基金和个人账户基金;2012年,社保基金会管理的基金有全国社保基金、个人账户基金以及广东省委托资金。虽然社保基金会管理的基金种类在变化,但全国社保基金的比例几乎为100%。
[1] QI J,NG W L.Liquidity Adjusted Intraday Value at Risk[EB/OL].(2009-01-17)[2014-03-02].
http://www.researchgate.net/publication/44260199_Liquidity_Adjusted_Intraday_Value_at_Risk
[2] Gregor W N F,Hendrik S.Forecasting liquidity-adjusted intraday Value-at-Risk with vine copulas[J]. Journal of Banking& Finance,2013,37(9):3334-3350.
[3] 谢福座,左柏云.基于La-Copula-EVT模型的我国股票市场风险价值研究[J].南京财经大学学报,2010(4):52-58.
[4] 江红莉,何建敏,胡小平.基于时变copula的La-VaR测度研究[J].重庆大学学报(社会科学版),2013,19(3):27-32.
[5] BEDFORD T,COOKE R M.Vines-a new graphical model for dependent random variables[J].The Annals of Statistics,2002,30(4):1031-1068.
[6] 黄恩喜,程希俊.基于pair-copula-GARCH模型的多资产组合VaR分析[J].中国科学院研究生院学报,2010,27(4):440-446.
[7] KIM D Y,KIM J M,LIAO S M,ET AL.Mixture of D-vine copulas for modeling dependence[J].Computational Statistics and Data Analysis,2013,64(1):1-19.
[8] MARCELO B R,PAULO S C.Analyzing the dependence structure of various sectors in the Brazilian market:A Pair Copula Construction approach[J].Economic Modeling,2013,35(9):199-206.
[9] 陈清平,程希骏.一个基于pair-copula法构建高维相依结构的研究[J].数理统计与管理,2013,32(2):232-239.
[10] 张高勋,田益祥,李秋敏.基于pair-copula模型的资产组合VaR比较研究[J].系统管理学报,2013,22(2):223-231.
[11] 江红莉,何建敏.基于pair-copula的社保基金投资组合风险测度研究[J].统计与信息论坛,2011,26(8):28-34.
[12] 江红莉,何建敏,李超杰.社保基金投资组合的动态风险测度研究[J].北京航空航天大学学报(社会科学版),2012,25(3):90-94.
[13] 张金清,李徐.流动性风险与市场风险的集成度量方法研究[J].系统工程学报,2009,24(2):164-172.
[14] SKLAR A.Fonctions de répartition à n dimensions et leurs marges[J].Publication de l’Institut de Statistique de l’Université de Paris,1959(8):229-231.
[15] AAS K,CZADO C, RIGESSI A,ET AL.Pair-copula constructions of multiple dependence[J].Insurance:Mathematics & Economics,2009,44(2):182-198.
[16] NEFTCI S N.Value at Risk Calculation,Extreme events,and Tail estimation[J].Journal of Derivatives,2000,7(3):23-37.
The measurement of national social security fund’s liquidity-adjusted VaR based on pair-copula
JIANG HONGLI, YAO HONGXING
Social security fund is the material basis of social insurance business’s development. Safety and liquidity are the first principles of social security fund investment. The risk management of National Social Security Fund, as a special fund that can be invested on the capital market, is particularly important. Aganist the inadequate research on the risk measurement of National Social Security Fund portfolio, the method of pair-copula-GARCH-EVT is proposed to measure the liquidity-adjusted market risk of investment portfolio. Compared with traditional multivariable copula model, pair-Copula model not only considers the influence of dimensions and but also can flexibly select the type of copula. The empirical research shows that the pair-Copula method is more accurate than traditional copula model in the aspect of measuring the liquidity-adjusted market risk of social insurance fund portfolio.
national social security fund; investment portfolio; liquidity-adjusted market risk; pair-copula; La_VaR
F842.61
A
1008-472X(2014)07-0047-08
2014-04-14
国家自然科学基金项目(71271103);江苏省高校哲学社科基金项目(2013SJB6300018);中国博士后科学基金第54批面上资助(2013M541603)。
江红莉(1982-),女,湖北随州人,博士后在读,江苏大学讲师,研究方向:风险管理;姚洪兴(1964-),男,江苏兴化人,江苏大学教授、博士生导师,研究方向:复杂系统分析。
本文推荐专家:
胡小平,东南大学,副教授,研究方向: 风险管理。
严忠,温州大学城市学院,教授,研究方向:数量经济学。
