基于Multisim的非正弦周期电流电路中有功功率的分析和计算

曹春雷

(金华广播电视大学)

1 非正弦周期信号

一切满足狄里赫利条件的周期函数都可以展开为傅里叶三角级数，所以非正弦周期电压(或电流)信号可分解成为傅里叶级数

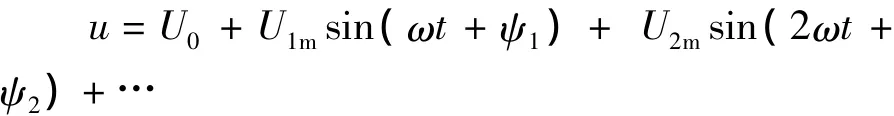
那么它就相当于一个直流电压和一系列不同频率正弦电压相叠加:

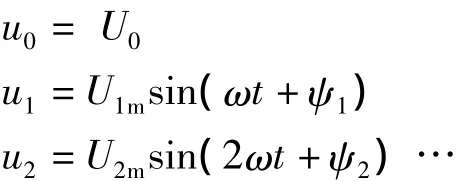
这样的电源接在线性电路中所引起的电流，可以用叠加原理来计算，即分别计算电压的恒定分量和各次谐波分量 u0、u1、u2、……单独存在时，在某支路中产生的电流分量 I0、i1、i2、……，而后把它们叠加起来，即为该支路的电流，即

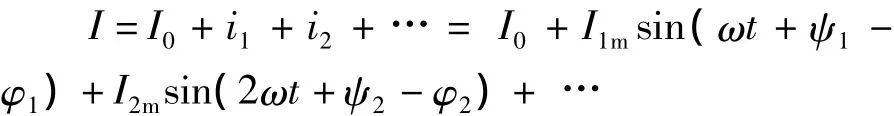
在计算非正弦周期电路中电压和电流的瞬时值时，可以用叠加原理进行计算.叠加定理只能用来计算电流和电压，不能直接用于计算功率，但是否可以移植叠加原理的思想到功率的计算，该文尝试在非正弦周期电路中，借鉴叠加定理的思想来计算它的有功功率，同时利用Multisim软件和实例中的理论计算同时来分析和验证非正弦周期电路中的有功功率等于恒定分量和各正弦谐波分量单独作用时所得到的有功功率之和，从而验证了有功功率在非正弦周期电路中的“可叠加性”.

2 Multisim软件介绍

Multisim是一种电路仿真软件，Multisim将电路图的绘制、实验仿真、测试分析结果的输出等全部集成在一个电路窗口中.仿真实验时电路图和仿真结果同时有效与可视，同时包括数字万用表、函数信号发生器、功率表、示波器、波特图仪等数十种虚拟仪表可使用.其中的功率表即电度表(Wattmeter)是用来测量功率和功率因数的仪器，电度表同时测量电压和电流两个值.要测量某个元件的功率，将电压档的两个端子并联在元件两端，将电流表串联在元件所在的支路中.该文就是利用功率表来进行分析和验证.

3 Multisim仿真实验和理论计算

(1)当U1=40sin(2000t)V单独作用时:

容抗 Xc1=1/ω1C=1/2000×2.5×10-6=200Ω，阻抗=360.56 Ω，电流有效值IR1=Ic1=U/Z1=0.111 A，相位差ψ1=-arctan Xc1/R=-33.7°，电流(2000t+33.7°)(A)，电阻电压(2000t+33.7°)(A)，有功功率为 P1=UR1*IR1=33×0.11 W=3.692 W.

其仿真实验结果如图1、图2所示:

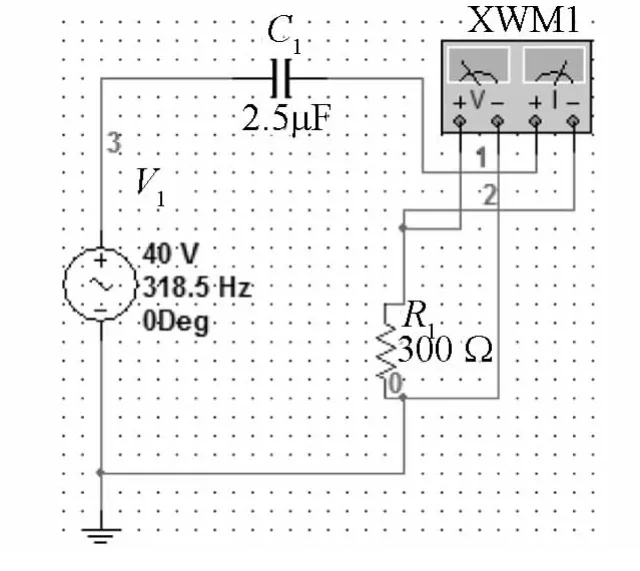
图1 U1单独作用时的仿真实验图

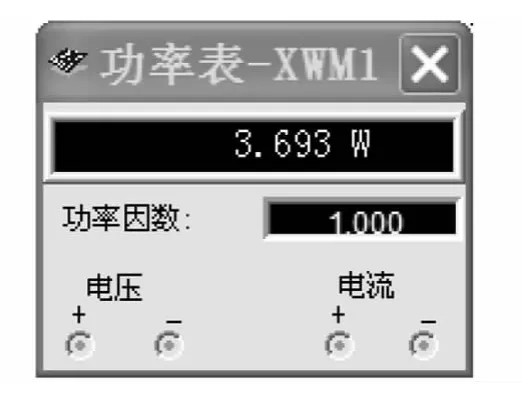
图2 功率表读数

从仿真实验结果看，忽略理论的误差值，理论计算值与仿真实验值基本相符合.

容抗 Xc2=1/ω2C=1/1000×2.5×10-6Ω =400 Ω，阻抗=500 Ω，电流有效值IR2=Ic2=U/Z2=0.16 A，相位差ψ2=-arctan Xc2/R=-53.1°，电流(A)，电阻电压(A)，有功功率为P2=UR2×IR2=48×0.16 W=7.68 W.

其仿真实验结果如图3、图4所示:

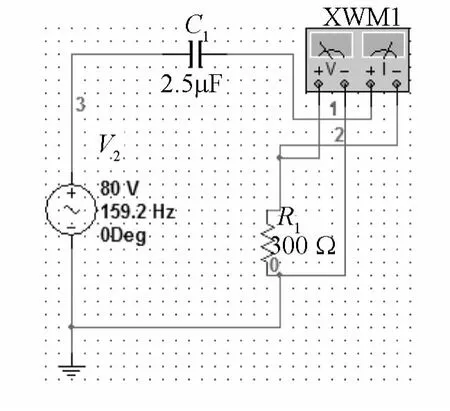
图3 U2单独作用时的仿真实验图

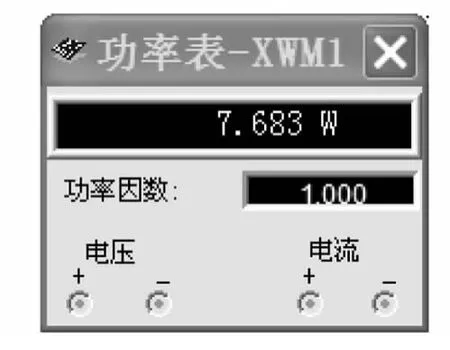
图4 功率表读数

从仿真实验结果看，忽略理论的误差值，理论计算值与仿真实验值基本相符合.

(3)当U3=100 V单独作用时，电容具有隔直流的作用，因此，电路中的电流和电阻电压为0，所以有功功率也为0.

其仿真实验结果如图5、图6所示:

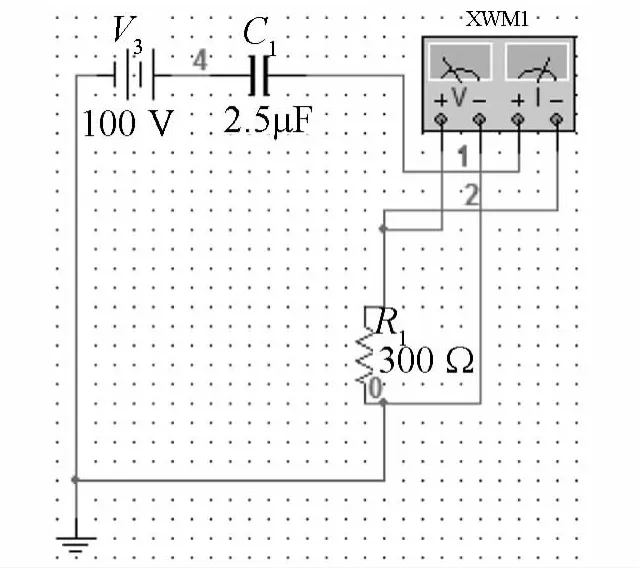
图5 U3单独作用时的仿真实验图

图6 功率表读数

从仿真实验结果看，理论计算值与仿真实验值基本相符合.

(4)当三个电源同时作用时总的有功功率仿真实验值为P=P1+P2+P3=(3.693+7.683+0)W=11.379 W，与理论计算P=P1+P2+P3=(3.692+7.68+0)W=11.372 W基本相符合.

其仿真结果如图7、图8所示:

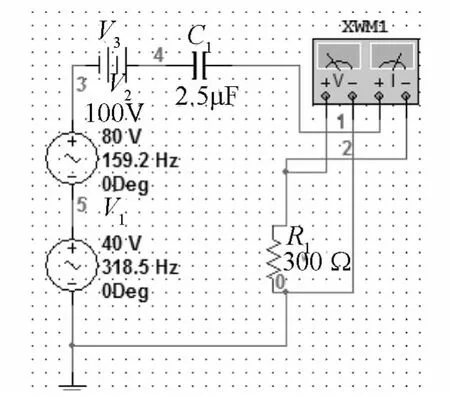
图7 三个电源同时作用时的仿真实验图

图8 功率表读数

从仿真实验结果看，忽略理论的误差值，理论计算值与仿真实验值基本相符合.

4 结束语

Multisim以其强大的虚拟电子元器件库和虚拟仪器仪表库给教学和实验带来了极大的便利.从仿真实验可以一目了然的看到结果，比理论计算来得简单和直观.从理论计算和仿真实验结果可以得出:非正弦周期电流电路中的有功功率等于恒定分量和各正弦谐波分量单独作用时所得到的有功功率之和.叠加定理不仅可以用来计算非正弦周期电流电路中的电流和电压的瞬时值，也可以借鉴“叠加定理”的思想来计算非正弦周期电流电路中的有功功率.非正弦周期电流电路中的计算可以归结为以下三个步骤:

(1)将非正弦周期电源电压分解成傅里叶级数，看作由恒定分量和各次正弦谐波分量串联的结果.

(2)利用叠加原理计算电压的恒定分量和各次正弦谐波分量单独存在时所产生的电流分量.并将每次单独作用得到的电流分量和电压分量的有效值分别相乘得出当次作用的有功功率数值.将当电源的恒定分量单独作用在电路中时，凡有电容的支路可视为开路，电流为0;对有电感的支路，不需要考虑电感的作用，都可视作短路.

(3)将所得的电流分量叠加起来，即为所需的结果，并将所有的有功功率数值相加即为总的有功功率.应该注意，不同频率的正弦电流或者电压量相加，必须用三角函数式或正弦波形来进行，不能用相量图或复数式.因为后两种方法是对同频率的正弦量而言的.更不能将各分量的有效值直接相加而求正弦周期量的有效值.

［1］ 秦曾煌.电工学:上册——电工技术［M］.北京:高等教育出版社，1990.

［2］ 人力资源和社会保障部教材办公室.电工基础教师用书［M］.北京:中国劳动社会保障部出版社，2010.

［3］ 董玉冰.Multisim9在电子电工技术中的应用［M］.北京:清华大学出版社，2008.

［4］ 周风献.叠加定理在非正弦周期电流电路中的应用分析［J］.青岛化工学院学报，2001.