水泥环力学完整性系统化评价方法
2014-10-24赵效锋管志川廖华林吴彦先
赵效锋,管志川,廖华林,吴彦先
(中国石油大学石油工程学院,山东青岛 266580)
收敛约束法是一种将理论基础、实测数据和工程经验结合为一体的隧道结构设计方法[1]。类比于隧道开挖过程中需要添加支护结构支撑开挖后的围岩收敛,石油工程中的钻井过程与其有一定的相似之处,即钻出井眼后需要下套管并注水泥固井以达到支撑井壁的作用。因此,可将隧道结构设计中的收敛约束法引入石油工程中,用于水泥环力学完整性评价。目前,国内对水泥环完整性的研究多集中于水泥环力学特性分析和影响规律上[2-6],缺乏系统化的水泥环完整性评价方法;尽管Fourmaintraux等[7]提出了基于收敛约束思想的系统响应曲线法可以直观地对水泥环进行力学完整性评价,但对于破坏程度的量化却没有涉及。笔者在弹塑性力学的基础上,结合收敛约束思想提出一种新的方法,以描绘水泥环的破坏形式及破坏程度,评价水泥环完整性和指导钻井工程设计。
1 隧道收敛约束法的引入
隧道收敛约束法又名特性曲线法。围岩向隧道中心产生变形即为收敛,支护提供压力约束这种收敛。隧道开挖后,围岩松弛并将应力逐渐传递给隧道支护结构,直到围岩和支护达到变形相等的稳定状态。收敛约束法基于弹塑性理论求出围岩特性曲线与支护特性曲线,找出特征曲线交点,用于判别隧道的安全状态。Deer[8]最早利用图解法阐述了隧道收敛约束法的基本概念,如图1所示。图1中收敛线表示围岩压力随隧道内边界径向位移增大而减小,约束线表示支护压力随外边界径向位移增大而增大;假如支护时围岩已产生初始位移u1,此时对应径向应力为p1,围岩仍处于弹性变形阶段。由于支护可变形,围岩与支护发生相互作用,最终围岩径向位移增大到u2时二者达到平衡,对应约束线与收敛线相交于a点,径向应力为p2,此时已进入收敛线的塑性段,围岩已发生塑性破坏,组合体结构失稳。

图1 收敛约束法原理图Fig.1 Principle diagram of convergenceconfinement method
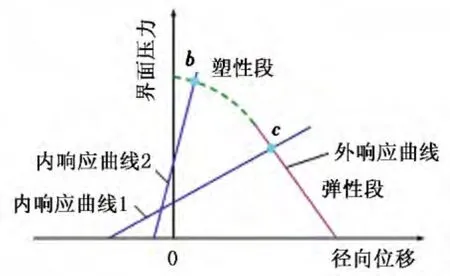
图2 系统响应曲线原理图Fig.2 Principle diagram of system response curve
同样,结合收敛约束思想提出的系统响应曲线(图2)由内外两条响应曲线组成,分别等同于收敛约束法中的约束线和收敛线,内响应曲线为弹性介质,所以为直线,外响应曲线为弹塑性介质,因此有直线段和曲线段,同样,二者反映的是接触界面上的力与位移关系,交点即是界面形变相等的平衡点。当内外两条响应曲线相交于弹性段(c点)时表明界面未产生塑性破坏,而相交于塑性段(b点)时则表明界面上产生了塑性破坏。
油气井井筒主要由套管、水泥环、地层3部分组成,因此有两个接触界面,即套管-水泥环界面(固井Ⅰ界面)和水泥环-地层界面(固井Ⅱ界面)。如图3所示,将系统响应曲线应用于油气井井筒绘制水泥环界面系统响应曲线时,界面一侧的另外两个部分将被视为一体进行求解。
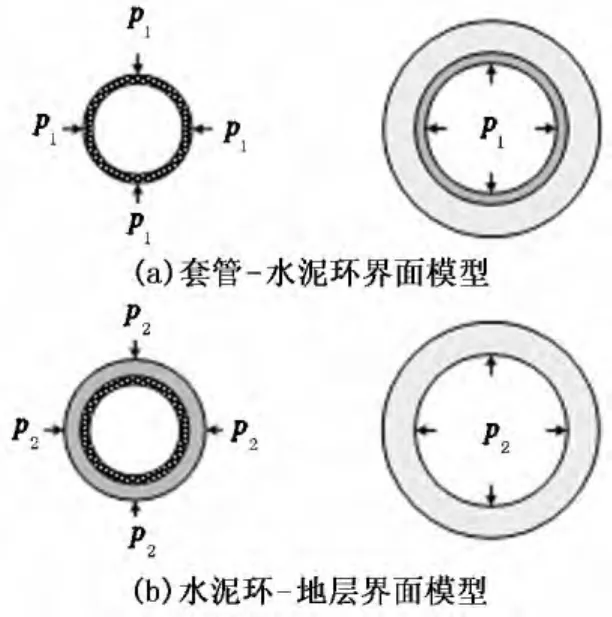
图3 水泥环系统响应曲线界面分解模型Fig.3 Interface decomposition model of cement system response curve
2 组合体力学模型
通过对井筒系统几何特征和边界条件的分析,若不考虑井筒纵向上位移的变化及轴向力,依据弹塑性力学理论,可将模型简化为厚壁圆筒的平面应变问题[2],组合体力学模型如图4所示。另外,求解过程须对模型作如下假设:①套管为各向均匀的弹性材料,水泥环、地层为弹塑性材料;②套管、水泥环、地层均为均匀壁厚的同心圆筒;③整个分析基于连续介质力学,且接触界面无相对滑动。

图4 套管-水泥环-地层组合体模型Fig.4 Combined model of casing,cement sheath and stratum
图4中,r0为套管内半径,mm;r1为水泥环内半径,mm;r2为水泥环外半径,mm;r3为近井地层外半径,mm;虚线为弹塑性区域分界线;rp1和rp2分别为水泥环和地层的塑性半径,mm;p0和p3分别为套管内压和地层外边界压力,MPa;p1和p2分别为套管-水泥环界面、水泥环-地层界面作用力,MPa。
3 系统响应曲线公式推导
公式推导过程中,假设压力为正,拉力为负。并选取Mohr-Coulomb准则作为水泥环的屈服准则。现实中由套管内压变化所导致的水泥环塑性破坏始于水泥环内壁并向外扩展,当套管内压大到使地层开始塑性变形时,水泥环早已完全塑性破坏,所以套管-水泥环界面较水泥环-地层界面更容易产生完整性问题,因此本文中暂不考虑水泥环-地层界面。
对套管-水泥环界面系统响应曲线计算时,须将水泥环和地层两部分合为一体求解,相当于两个厚壁筒紧密嵌套,而对套管则单独进行求解,相当于单层厚壁筒。
3.1 弹性阶段
由拉梅问题的基本解可得套管区域外径处位移为

式中,G 为剪切模量,GPa;υ 为泊松比;下标1、2、3表示套管、水泥环和地层区域。
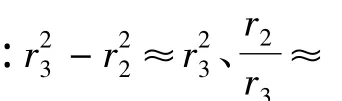
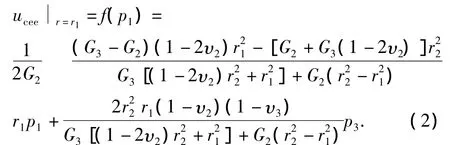
3.2 塑性阶段
在套管内压过大的情况下有可能出现水泥环塑性破坏,当界面作用力p1达到水泥环弹性极限时,水泥环内壁开始屈服,此时塑性半径等于水泥环内径;当p1逐渐增加时,水泥环内的弹塑性状态也随着改变,塑性半径不断增大,直到完全塑性变形。
平面应变问题中的切应力为0,则正应力σr、σθ和σz均为主应力,在外挤压力小于内压情况下,由拉梅公式基本解可以得出厚壁筒中σθ<0、σr>0且有 σθ< σr,由轴向应变 εz=0可以得 σz=υ(σr+σθ),故σz为中间主应力,3个主应力的排序为σr≥σz≥σθ,则Mohr-Coulomb屈服准则的形式为

其中
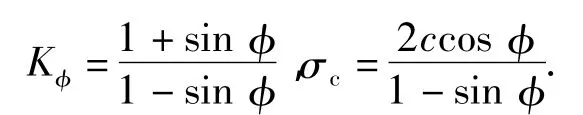
式中,σr为径向应力,第一主应力,MPa;σθ为周向应力,第三主应力,MPa;φ为内摩擦角,(°);c为黏聚力,MPa。
rp1为水泥环弹性区与塑性区分界线,根据弹塑性力学理论,可将水泥环弹性区与塑性区视为双层厚壁筒求解,并根据r=rp1处应力、位移的连续性条件,最终推导出塑性阶段水泥环-地层区域内径处位移为

其中,rp1和p2满足方程组:
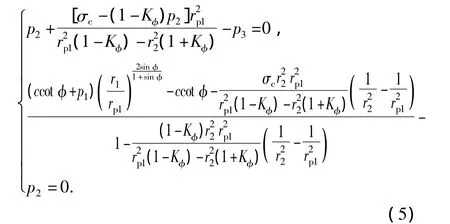
式(5)为超越方程,可以用试算法求出。
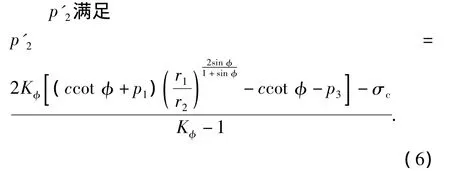
3.3 拉伸破坏临界线
在水泥环内压大于外压的情况下,水泥环应力超过其抗拉强度时可能产生拉伸破坏,则拉伸破坏临界线需满足以下条件。
首先,根据最小主应力σθ等于水泥环抗拉强度,可得


式中,σTS为水泥环抗拉强度,MPa。
通过判断响应曲线位移平衡后的交点与拉伸破坏线的相对位置来判断是否发生拉伸破坏,因此还应该满足临界线上的点均为响应曲线的交点,即
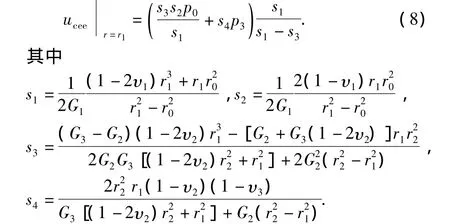
联立方程(7)和(8),即可得出拉伸破坏临界线的表达式。
4 水泥环力学完整性评价方法
4.1 水泥环的破坏形式
在油气井的长期服役过程中,造成水泥环力学完整性失效的破坏形式主要有:①Ⅰ界面微间隙。Ⅰ界面微间隙是水泥环长期完整性失效的主要形式之一。有分析指出,套管内压交变作用下的水泥环塑性残余变形是导致Ⅰ界面微间隙产生的主要原因。②Ⅱ界面微间隙。排除施工工艺、过程等不利因素,在油井长期服役过程中,相比Ⅰ界面,在套管内压力交替变化条件下的Ⅱ界面不易产生微间隙。③剪切破坏。水泥环的剪切破坏是由于套管内压过大所造成的,其破坏方向与界面法线方向呈一定角度。④径向裂纹。径向裂纹是水泥环的周向拉伸破坏的表现形式,而套管内压过大及水泥环宏观体积收缩是造成径向裂纹的主要原因。
4.2 水泥环力学完整性的系统响应曲线
基于以上水泥环的破坏形式及破坏机制的分析,分别对水泥环的系统响应曲线所表示的结果进行说明。计算中将径向位移朝向井筒轴线方向记为正。水泥环响应曲线如图5所示。
如图5(a)所示,套管、水泥环-地层区域分别在一定套管内压和围岩应力的作用下膨胀和收缩,因此当水泥环界面压力为0时内外两条响应曲线分别有相应的初始位移(图中a和b两点)。随着界面压力的不断增大,套管径向位移不断增大,水泥环-地层区域径向位移不断减小,直到二者相交于一点c,此时界面应力相等且径向位移相等,达到稳定状态,结果显示平衡交点c位于水泥环-地层区域响应曲线的弹性段且在拉伸破坏临界线以下,因此并未发生剪切破坏及拉伸破坏,水泥环完整性良好。
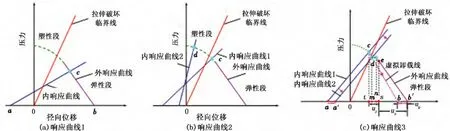
图5 水泥环系统响应曲线Fig.5 Cement system response curve
相比曲线1,图5(b)中曲线2中内响应曲线1的平衡交点c位于水泥环-地层区域响应曲线的塑性段及拉伸破坏临界线以下,此种工况下水泥环只产生了剪切破坏,而没有拉伸破坏;内响应曲线2的平衡交点d位于水泥环-地层区域响应曲线的塑性段且位于拉伸破坏临界线以上,此种工况下水泥环不但产生剪切破坏并且出现了径向裂纹。
在油气井建井及生产过程中,不同阶段、不同工况下套管内压均不相同,微间隙的产生取决于前后两个工况套管内压的变化,如果水泥环在高应力作用下产生了塑性应变,套管压力随之降低则很可能产生微间隙。因此,微间隙的产生和评价是一个动态的过程。
如图5(c)所示,内响应曲线1与外响应曲线相交于c点,表示在一定水泥环界面压力下套管和水泥环-地层区域达到稳定状态,根据c点的位置可以判断出水泥环发生了剪切破坏和拉伸破坏;当套管内压减小时,内响应曲线1将会向径向位移增大方向平移(图中内响应曲线2),根据弹塑性力学理论,当压力超过材料的屈服极限时,卸压后其应力-应变曲线将不再沿原路径返回。因此,当水泥环-地层区域发生塑性破坏后界面压力减小,其位移也不再沿收敛线变化,而是沿图中的虚拟卸载线变化。根据塑性理论,总位移可以分解为弹性位移ue和塑性位移up,且在变形不大时,多数材料的塑性应变和残余应变近似相等。图5(c)中e点为弹塑性分界点,c点和e点二者所对应位移的差值即为残余应变所对应的塑性位移,bb'是卸载后径向位移与初始位移的差值即为残余应变所对应的塑性位移,即ts=bb',因此可以通过b点位置得出水泥环虚拟卸载线。图5(c)中d点为内响应曲线2与虚拟卸载线的交点。若水泥环-地层区域沿原收敛线卸载,则在此平衡界面压力下所对应的位移应该在n点处。由于虚拟卸载线的斜率大于原收敛线,因此随着水泥环界面压力的减小,水泥环-地层区域位移沿虚拟卸载线变化比原外响应曲线要快,二者之间存在位移差mn,tm为套管内压减小所产生的卸载位移,当卸载后达到稳定状态时,如果套管的卸载位移tm比水泥环-地层区域的卸载位移mn大,即tm>mn,二者间产生尺寸为(tm-mn)的微间隙;若状态稳定,套管内压降低所产生的位移不足以抵消水泥环-地层区域的卸载位移差时,即tm<mn,则不会产生微间隙。
5 实例分析
从文献资料中选取一口垂直井的数据作为实例,该井井眼规则,固井质量良好且套管、水泥环完全居中,水泥环短期完整性良好,其几何特征及材料参数见表1。
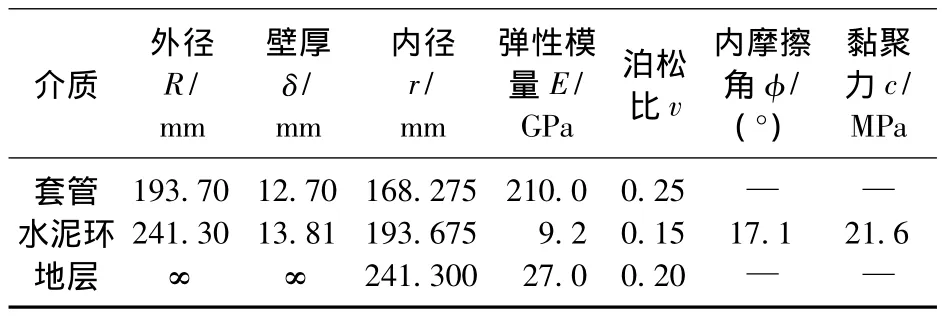
表1 实例井几何特征及材料参数Table 1 Geometrical characteristic and material parameter of sample well
该井垂深4.575 km,水泥返高4.1175 km;在油井的整个生命周期中,近井区域的水平地应力未发生变化为92 MPa,在不同的作业阶段和工况下,套管内压力随着套管内流体介质及井口压力的不同而发生变化,计算过程中对套管内压依次进行编号,如图6所示。
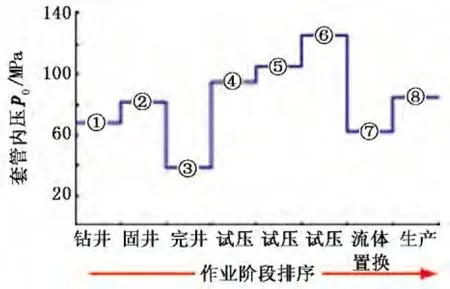
图6 不同作业阶段套管内压变化排序Fig.6 Casing pressure order at different operation stages
利用以上系统响应曲线法对油气井生命周期中的水泥环力学完整性进行评价,评价结果如图7所示。
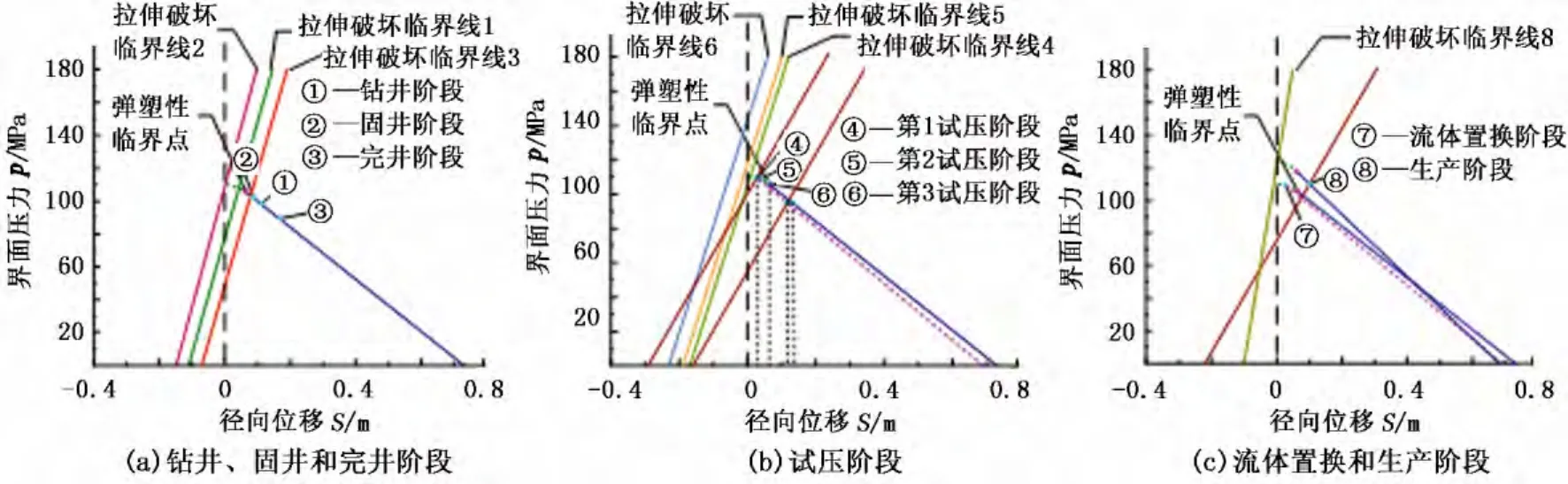
图7 水泥环力学完整性评价Fig.7 Evaluation of cement mechanical integrity
在钻井、固井、完井前3个作业阶段中(图7(a)),套管和水泥环-地层区域达到稳定状态时的交点均未超过水泥环-地层区域的弹塑性临界点,整个过程位于响应曲线的弹性段,水泥环完整性良好。随着该井作业的继续进行(图7(b)),当油井处于试压第1个阶段时,水泥环-地层区域已进入塑性段,直到试压的第3个阶段,水泥环-地层区域进入完全塑性阶段,由于试压过程套管内压力没有降低,所以不可能产生微间隙。当套管中流体被置换时(图7(c)),套管内压降低,水泥环-地层区域响应曲线沿虚拟卸载线进行卸载,达到稳定状态后产生了0.07 mm的微间隙;当生产阶段套管内压再次上升时,在上一阶段的界面位置基础上绘制系统响应曲线,在产生塑性破坏后再次加载响应曲线存在应变硬化的现象,在界面压力为110.5 MPa时再次与套管达到稳定状态,而此时水泥环-地层区域并未发生塑性破坏,平衡压力距离弹塑性临界点118 MPa仍有一段距离,但由于此前水泥环已发生过塑性破坏,存在破碎区,所以水泥环的完整性依然会失效。
6 结论
(1)将隧道结构设计中的收敛约束法引入石油工程中,提出的水泥环力学完整性评价方法可行,运用该方法可以对水泥环力学完整性进行直观的评价,同时可以对破坏程度进行量化。
(2)水泥环力学完整性的评价需要纵观油气井的整个生产作业历史。若前一阶段水泥环完整性已经发生失效,会对后续阶段的完整性产生影响。
(3)水泥环力学破坏准则的选取与破坏机制的研究在水泥环力学完整性评价中非常重要,其理论体系还有待于进一步研究。
[1] 唐雄俊.隧道收敛约束法的理论研究与应用[D].武汉:华中科技大学土木工程与力学学院,2009.TANG Xiongjun.Study on the convergence-confinement method and its application in tunnel construction[D].Wuhan:School of Civil Engineering and Mechanics,Huanzhong University of Science & Technology,2009.
[2] 李军,陈勉,柳贡慧,等.套管、水泥环及井壁围岩组合体的弹塑性分析[J].石油学报,2005,26(6):99-103.LI Jun,CHEN Mian,LIU Gonghui,et al.Elastic-plastic analysis of casing-concrete sheath-rock combination[J].Acta Petrolei Sinica,2005,26(6):99-103.
[3] 李国.井下工况及载荷对水泥环的影响研究[D].成都:西南石油大学石油工程学院,2006.LI Guo.The study of effect on cement sheath by downhole conditions and load[D].Chengdu:School of Petroleum Engineering,Southwest Petroleum University,2006.
[4] 曾德智,林元华,李双贵,等.非均匀地应力下水泥环界面应力分布规律研究[J].石油钻探技术,2007,35(1):32-34.ZENG Dezhi,LIN Yuanhua,LI Shuanggui,et al.Study of stress distribution of cement sheath cross section under non-uniform formation stress[J].Petroleum Drilling Techniques,2007,35(1):32-34.
[5] 李勇,刘硕琼,王兆会.水泥环厚度及力学参数对其应力的影响[J].石油钻采工艺,2010,32(4):37-40.LI Yong,LIU Shuoqiong,WANG Zhaohui.Effect of cement thickness and its mechanical parameters on cement stress[J].Oil Drilling & Production Technology,2010,32(4):37-40.
[6] 赵效锋,管志川,吴彦先,等.均匀地应力下水泥环应力计算及影响规律分析[J].石油机械,2013,41(9):1-6.ZHAO Xiaofeng,GUAN Zhichuan,WU Yanxian,et al.Analysis of stress property and effect law of cement sheath under uniform in-situ stress[J].China Petroleum Machinery,2013,41(9):1-6.
[7] FOURMAINTRAUX D,BOIS A-P,FRANCO C,et al.Efficient wellbore cement sheath design using the SRC(system response curve)[R].SPE 94176,2005.
[8] DEER D U,PECK R B,MONSEES J E,et al.Design of tunnel liners and support systems[R].U.S.Department of Transportation,Office of High Speed Ground Transportation,1969.
