永磁同步直线电机模糊PID控制及仿真

2014-10-22许道金杨庆东

机械工程与自动化 2014年1期

许道金，杨庆东，衣杰

（北京信息科技大学机电工程学院，北京 100192）

0 引言

传统的数控机床进给方式多以伺服电机带动滚珠丝杠来完成，但随着人们对加工精度和效率要求的提高，传统的进给方式由于传动误差大、进给速度及加速度低、机械噪声大、传动效率低等诸多问题已难以满足人们的要求。直线电机进给代替丝杠进给消除了中间的传动环节带来的误差，极大地提高了系统的进给速度和运动精度。但是电机和执行终端没有了中间的缓冲环节，使得负载的变化直接作用在电机上，这给电机的控制带来难度。传统的PID控制，由于比例、积分和微分系数K p，K i及K d的数值固定，在变负载、慢时变参数的情况下，需要人工干预去重新整定控制器的参数，这既降低了工作效率，又增加了成本，且效果不佳。本文将传统的PID控制和模糊控制的优点结合到一起，设计开发了模糊PID控制器，并进行了试验仿真，得到很好的结果。

1 直线电机的数学模型

1.1 直线电机的电压平衡方程

取永磁体行波磁场的方向为d轴，而q轴顺着旋转方向超前d轴90°电角度。因为由永磁体产生的磁电动势为常值，在次极上无阻尼绕组，所以，永磁同步直线电机的d，q轴模型电压方程式分别为：

其中：Ra为直线电机动子的电阻；L d和L q分别为d轴和q轴的电感；i d和i q分别为d轴和q轴的电流；ω＝（v／p nτ）×2π，p n为直线电机的极对数，τ为极距，v为直线电机的线速度；ψd和ψq分别为直轴和交轴的磁链；ψf为永磁体磁链［1］。

1.2 直线电机电磁推力及运动学方程

不考虑文波推力和端部效应等的影响下，直线电机的电磁推力方程为：

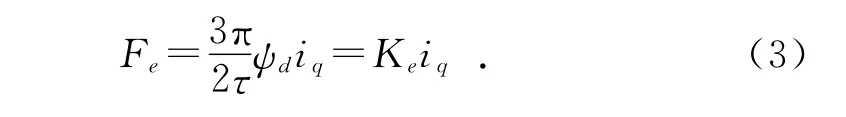
其中：K e＝表示电磁推力系数，为一个定值。此时，电磁推力F e与q轴电流i q成正比。

直线电机的运动学方程为：

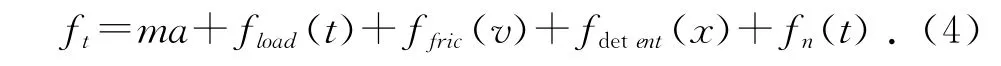
其中：f t为电机的电磁推力；x，a分别为物理位移和加速度；f load（t）为负载力；f fric（v）为摩擦力；fdetent（x）为磁阻力；f n（t）为其他干扰力；m为直线电机动子的总质量。摩擦力中对永磁同步直线电机控制系统影响最大的力是动摩擦力和黏滞摩擦力［2］，f f ric（v）＝μN＋Bv（其中μ为动摩擦因数，N为正压力，B为阻尼）。

2 模糊PID控制器的设计

2.1 模糊控制器结构及其工作原理

参数自调节模糊PID控制器结构如图1所示。此二维模糊控制器采用了2个输入、3个输出，其中2个输入为偏差e和偏差的变化率｜ec｜（即）。利用模糊控制规则输出修正量（ΔK p，ΔK i及ΔK d）实时对PID进行参数修正，以满足不同误差和误差变化率对PID参数自调节的要求，从而使被控对象具有更加良好的动态特性和静态特性。in和out分别为整个系统的输入和输出。

图1 参数自调节模糊PID结构图

由永磁同步直线电机的数学模型可建立速度控制结构图，如图2所示。

图2 直线电机速度控制结构图

我们利用模糊规则整定PID三个参数的原则为：

当系统偏差绝对值｜e｜较大时：应取较大的K p和较小的K d，使系统响应加快。

当系统偏差绝对值｜e｜中等时：应取较小的K p以及适当的K i和K d，以使得系统具有较小的超调量。

当系统偏差绝对值｜e｜较小时：应取较大的K p和K i以及适当的K d，避免在平衡点附近出现振荡，使系统具有较好的稳态性能［3］。

2.2 模糊控制器的设计

首先定义模糊控制器的输入，系统偏差绝对值｜e｜和误差变化率｜ec｜的论域为｛0，2，4，6｝，模糊子集为｛Z，S，M，B｝。输出ΔK p，ΔK i及ΔK d的论域为｛-6，-3，0，3，6｝，模糊子集分别为｛NB，NS，ZE，PS，PB｝。为了尽量减少计算机的计算时间，输入、输出均采用三角隶属函数，如图3及图4所示。

图3 输入的隶属函数图

针对ΔK p，ΔK i及ΔK d三个参数分别规定的模糊控制规则表，如表1所示。

最后，对输出变量进行去模糊化处理。经过前面的模糊推理后，模糊控制器输出的3个调整参数均为模糊量，所以必须要对其进行去模糊化，取得精确量以计算输入到PID控制器的3个参数K p，K i，K d。

图4 输出的隶属函数图

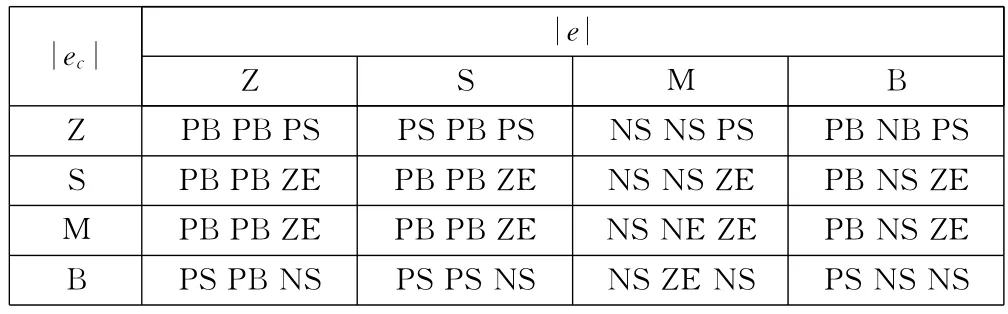
表1 模糊规则表（ΔK p，ΔK i，ΔK d）

利用重心法解模糊过程如图5所示。

图5 重心法解模糊过程图

3 直线电机的模糊控制系统仿真及结果分析

本文在MATLAB中应用模糊FIS.Editor编写输入及输出隶属函数及模糊规则，然后在simulink中构建如图6所示的交流永磁同步电机模糊PID控制系统模型。为了反映两种控制系统的抗干扰能力，分别在200 ms时加入相同的负载干扰讯号。

图6 PMLSM系统控制仿真图

此时系统参数为：直线电机动子的电阻Ra＝4.05 Ω，L q＝37 m H，动子质量m＝70 kg，ψf＝0.24 Wb。仿真得到系统的速度步进响应曲线和有负载干扰情况下的速度响应曲线如图7和图8所示。从模拟的结果可以得知，模糊PID对步进函数的响应，在调整时间和系统超调量方面都远远优于传统PID；在外加干扰时模糊PID的调整时间也明显小于传统PID。因此与传统PID相比，模糊PID不仅具有较强的跟踪性能，而且有较强的鲁棒性。

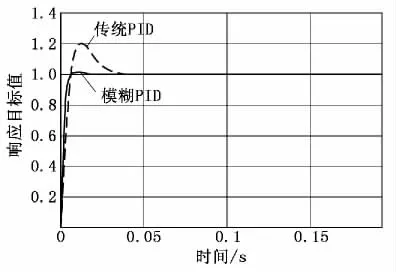
图7 系统的速度步进函数响应曲线

4 结论

本文结合了传统PID控制和模糊控制的优点，设计研发模糊PID控制器。经过实际的模拟试验表明，采用本文所设计的模糊参数自调节PID控制器，反应时间由原先的80 ms减少到40 ms超调量减少到原来的十分之一。即使出现干扰的状况下，也可以获得非常令人满意的控制效果。达到了反应时间变短、超调量降低、鲁棒性增强的目的，其控制效果明显。优于传统的PID控制。