干摩擦下含双侧间隙碰撞振动系统的动力学分析❋
2014-10-22李贵杰
周 鹏,李贵杰,黄 剑
(1.兰州交通大学 机电工程学院,甘肃 兰州 730070;2.兰州交通大学 数理学院,甘肃 兰州 730070)
0 引言
机械工程领域,系统存在的间隙使系统发生碰振,由摩擦引起的碰振是强非线性和非光滑的,众多学者对此进行了研究。Shaw[1]对双面碰振系统进行研究,发现了斯梅尔马蹄。Cone[2]研究含干摩擦的双面冲击振子,得到系统存在黏滑碰撞。Vir gin[3]研究了包含摩擦阻尼的双边谐激励碰撞系统的全局动力学,说明擦边分岔是系统行为突变的来源。Ding[4]研究强共振情形下多自由度碰振系统的次谐分岔与霍普夫分岔。本文给出含间隙和干摩擦的两自由度碰振系统的运动方程和衔接条件,采用数值迭代法研究干摩擦和带速对系统动力学的影响。
1 力学模型及运动方程
1.1 力学模型
图1为一类具有质量分别为M1和M2的振子的碰振系统的动力学模型。振子M1由黏性阻尼C1和刚度为K1的弹簧与振子M2相连接,振子M2由阻尼C2和刚度为K2的弹簧与刚性平面连接,作用在M1和M2的简谐力为Pisin(ΩT+τ)(其中,Ω为角速度,τ为初相角,T为时间,Pi分别为作用在两振子的外激励,i=1,2),皮带与两质块之间的干摩擦力分别为F1和F2。取正方向为水平向右建立坐标系,两振子的质心作为原点,X1和X2分别表示M1和M2的位移。当M1的位移为B(或-B)时,将与刚度为K0的弹性约束碰撞,皮带速度为V。一定时间后M1改变运动方向,又以新的初值运动,再与约束碰撞,如此往复。
1.2 运动微分方程
在任意连续两次碰撞之间(|X1|<B)摩擦碰振系统的运动方程为:

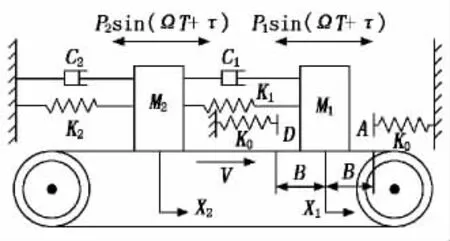
图1 两自由度含间隙和干摩擦碰振系统模型
振子与皮带之间摩擦力为:
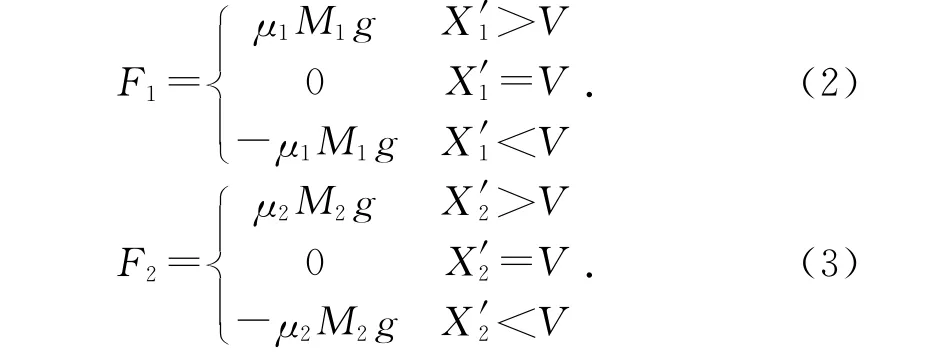
其中:μ1,μ2为滑动摩擦系数。振子M1与弹性约束碰撞时的弹簧力为:

设μm=,则系统的量纲一方程:

1.3 滑动、黏滑及碰撞
图1所示碰振系统的模型是分段光滑的,在一完整运动过程中,令M1除摩擦力外所受的合外力=|(1-f20)sin(ωt+τ)-2ζv+2-x1+x2-f(x1,v)|;M2除摩擦力外所受的合外力=下面分5种不同情况进行讨论。
(1)=v,≠v,则黏滑,滑动,系统运动方程为:
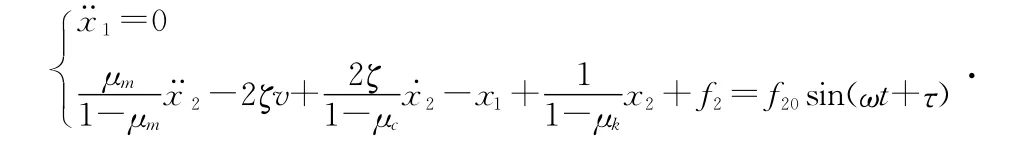
直到>f s1(f s1为最大静摩擦),M1黏滑结束,开始滑动。
(2)≠v,=v,则M2黏滑,M1滑动,系统运动方程为:
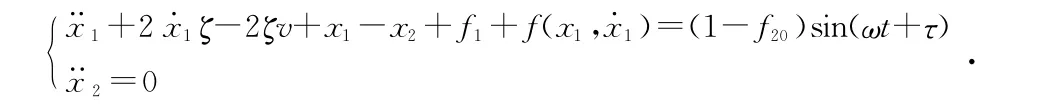
直到>f s2时(f s2为最大静摩擦),M2黏滑结束,开始滑动。
(3)=v=v,则M1,M2都发生黏滑,系统运动方程:

直到>或>f s2时,M1或M2开始滑动。
4x1≠v x2≠v M1M2都发生滑动。直到≥f s1时M1开始黏滑,或≥f s2时M2开始黏滑。
(5)|x1|=δ,M1与约束发生碰撞。
系统在上述5种运动状态间转换。
2 系统的周期运动与稳定性
研究运动方程的映射图,每次迭代都表示质块M1和约束发生一次碰撞。令θ=ωt,取庞加莱截面∑={(x1,x,x2,,θ)∈R4×S|x1=δ,>0}即质块M1位移为δ且速度大于零。假设在n个激励周期内,经历q次右碰,p次左碰,k次黏滑,用n-p-q-k-I表示不含黏滑的周期碰撞,n-p-q-k-II表示含黏滑的周期碰撞。其无量纲时间t为0,则下次碰撞前瞬时,t恰好为2nπ/ω。通过映射Q可以得到其Jacobi矩阵DQ,根据DQ的特征值λ1能判断出图1所示碰振系统的周期运动与局部分岔。
3 数值分析
着重研究带速和干摩擦对系统动力学的影响。取无量纲参数:μm=0.2,μk=0.1,μc=0.2,δ=0.01,ζ=0.2,f20=0.5,μk1=0.3,μk0=100,v=0.1。图2为取不同的摩擦因数f u=1和f u=0.1,当ω由0到5变化时的全局分岔图。由图2可以看出:随着摩擦力增大,在激励频率较小时只影响到穿越截面的速度大小;在激励频率较大时,系统从存在混沌带和一些周期窗口演化成倍周期混沌最后到周期运动。
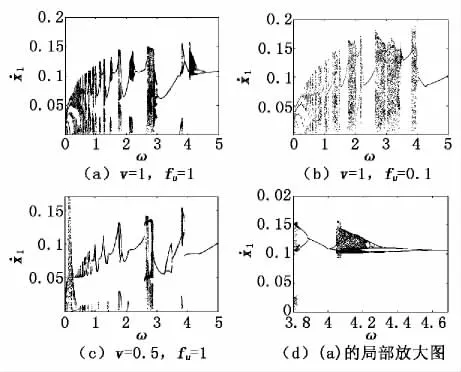
图2 M 1分岔图
通过对图2(a)和图2(c)的比较可知,干摩擦一定,当皮带轮速度较低时,系统混沌区域宽度变窄,低频区域尤其明显,周期运动明显增加,混沌区域明显减少,质块M1与两侧约束的冲击速度减小。增大皮带轮速度v,系统的周期窗口增多,混沌与周期运动交替出现,质块与两侧约束的冲击速度变大。
图3给出了系统的周期倍化过程。ω∈(4.616,5)时M1为非对称的周期1-1-1-1-II运动,此段位移内M1与皮带轮黏滑。ω∈(4.341,4.616)时演变为非对称的周期2-2-2-1-II运动,在ω=4.616处出现倍化分岔。在ω=(4.266,4.341)变迁为4-4-4-2-II运动。在ω=(4.05,4.266)时系统由倍化分岔进入混沌。在ω= 4.002 4.05 时系统由混沌退化为周期2运动,并在ω=4.002处进入逆倍化分岔。从时间响应图或相图都能看出质块在皮带轮上的黏滑运动,并且展现了系统运动状态随着摩擦因数的变化而变化。
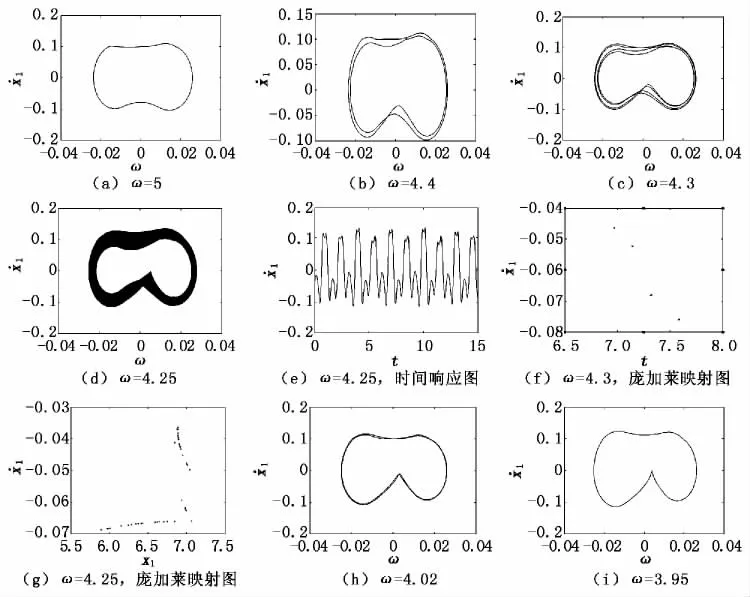
图3 周期倍化过程
4 结论
(1)系统的动力响应存在叉式分岔、倍周期分岔和逆倍化分岔。
(2)带速一定,摩擦力较大时对系统动力学性能影响明显。在频率比较小时质块穿越的速度影响明显,频率比较大时系统的拓扑结构影响明显。
(3)干摩擦一定,在小带速时导致系统混沌区域宽度变窄,低频区域尤其明显,周期运动明显增加,混沌区域明显减少。
[1]Shaw S W.The dynamics of a hArmonically exited system having rigid amplitude constraints[J].Jour nal of Applied Mechanics,1985,52(2):453-464.
[2]Cone K M.A nu merical study of an i mpact oscillator with addition of dry friction[J].Journal of Sound and Vibration,1995,188(5),659-683.
[3]Vir gin L N.Grazing bif urcations and basins of attraction in an i mpact-friction oscillator[J].Physica D,2001,132:43-57.
[4]Ding W C,Xie J H.Dynamical analysis of two-parameter family for a vibro-impact system in resonance cases[J].Journal of Sound and Vibration,2005,287(1):101-115.
[5]陆启韶,金俐.具有刚性约束的非线性动力系统的局部映射方法[J].固体力学学报,2005,26(2):132-138.
[6]罗冠炜,谢建华.碰撞振动系统的周期运动和分岔[M].北京:科学出版社,2004.
[7]金栋平,胡海岩.碰撞振动及其典型现象[J].力学进展,1999,29(2):155-163.
[8]罗冠炜.塑性碰撞机械振动系统的周期运动和分岔[J].机械工程学报,2006,10(10):87-96.
